Видимо, это осень так влияет, что за последний месяц на PostgreSQL уже и в «Морской бой» играли, и «Жизнь» Конвея эмулировали… Что уж оставаться в стороне! Давайте и мы потренируем мозг в реализации нетривиальных алгоритмов на SQL.
Тем более, сегодняшняя тема родилась из обсуждения моей же статьи «PostgreSQL Antipatterns: «Бесконечность — не предел!», или Немного о рекурсии», где я показал, как можно заменить рекурсивное чтение иерархичных данных из таблицы на линейное.
Прочитать-то мы прочитали, но ведь чтобы для вывода упорядочить элементы дерева в соответствии с иерархией, уж точно придется воспользоваться рекурсией! Или нет? Давайте разберемся, а заодно решим на SQL пару комбинаторных задач.

Давайте возьмем в качестве примера прочитанный из базы набор записей чего-то вроде справочника сотрудников. Они образуют ориентированное дерево из отделов и работающих в них сотрудников, которое выглядит примерно вот так:

Точнее, это нам хочется, чтобы оно выглядело именно так — дочерний узел под родительским, правильная сортировка «детей» внутри одного предка, красивые отступы… Но база-то нам отдаст записи отсортированными в том порядке, который удобнее ей — скорее всего, по первичному ключу
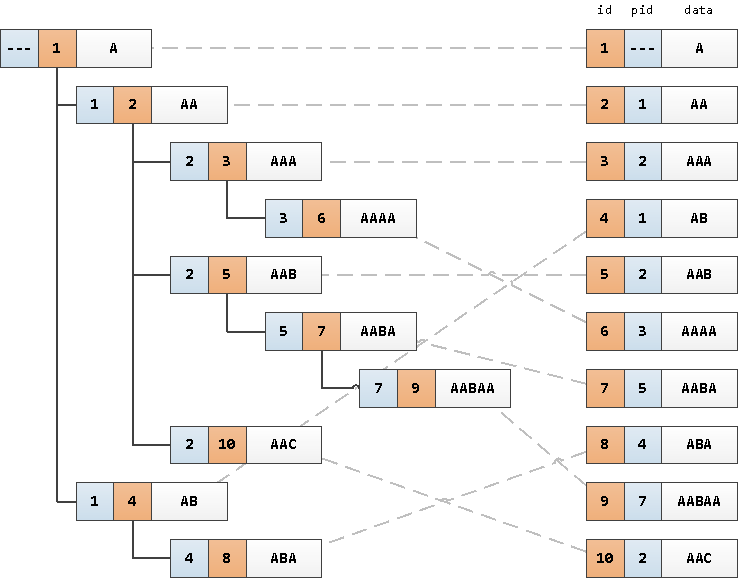
Давайте все-таки сначала формально определим те правила, которым должен отвечать искомый порядок записей:
Второе требование отражает привычные для пользователя паттерны, когда папки внутри одного каталога отображаются отсортированными по названию, а ответы на сообщение в ветке форума — по времени.
Мы, для простоты, возьмем в нашем примере в качестве такого ключа —
Собственно, а что мы такое можем сконструировать, чтобы сортировка этого «чего-то» давала нам желаемый результат?
Давайте для каждого элемента дерева вычислим «путь» — цепочку из прикладных ключей всех элементов, которые надо пройти от корня, чтобы его достигнуть:

Но если на каждом шаге такого пути мы сортируем элементы согласно прикладному ключу, то и массивы, составленные из этих ключей, будучи отсортированными, дадут нам искомый порядок записей!
Сначала воспользуемся наиболее традиционным и очевидным способом получения нужного нам результата — рекурсивным запросом:
А теперь вернемся к началу статьи и подумаем, как же все-таки для той же самой задачи мы можем создать нерекурсивное решение. В этом нам поможет…
Пусть у нас есть исходный массив
Достаточно очевидно, что при длине массива
Обратим внимание, что каждой комбинации элементов соответствует комбинация позиций этих элементов в исходном массиве, если пронумеровать их с нуля. А каждой такой комбинации — число в N-ричной системе счисления:
Решение становится достаточно очевидным:
Но в оригинальном наборе у нас каждый элемент был уникален, а в полученных нами комбинациях это правило не соблюдается. Исправим, получив все возможные перестановки. Для этого отфильтруем из
Это дает нам все возможные перестановки исходного набора:
Можно использовать и «неэкспоненциальный» алгоритм на основе «тасований», работающий за
Сделаем шаг чуть в сторону и научимся генерировать все подмножества исходного набора с сохранением порядка. То есть для нашего набора
В принципе, задача очень близка к первой решенной нами. Только вместо позиции двоичная «цифра» означает отсутствие или наличие соответствующего элемента в результирующем наборе:
Поскольку двоичная арифметика представлена в компьютерах гораздо эффективнее, мы можем воспользоваться функциями работы с битовыми строками:
Теперь, вооруженные всеми приведенными выше алгоритмами, попробуем найти решение нашей задачи сначала в общем виде, а затем разберем один из типичных частных случаев.
Для начала воспользуемся тем фактом, что в качестве элементов пути, который идентифицирует конкретную запись, можно использовать уникальные ключи промежуточных записей — в нашем случае это
Но сортировать по такому пути, конечно, будет некорректно — поэтому для дальнейшей сортировки превратим
Корректный путь от корня до конкретного элемента обладает следующими свойствами:
Итак, намечаем план действий:
Можно и попроще, если заранее известно, что порядок «детей» внутри одного «родителя» определяется некоторым сквозным ключом. Например, это может быть некоторый монотонно возрастающий timestamp сообщений в ветке форума или, как в нашем случае, первичный ключ типа
В таком случае, мы уже точно знаем порядок следования идентификаторов записей в нужном нам пути — он совпадает с общей сортировкой по этому ключу. И нам надо только выкинуть лишние id из списка всех предстоящих:
Понятно, что производительность таких «экспоненциальных» решений не особо велика и применять «в бою» надо с большой осторожностью, но как гимнастика для ума — вполне.
Тем более, сегодняшняя тема родилась из обсуждения моей же статьи «PostgreSQL Antipatterns: «Бесконечность — не предел!», или Немного о рекурсии», где я показал, как можно заменить рекурсивное чтение иерархичных данных из таблицы на линейное.
Прочитать-то мы прочитали, но ведь чтобы для вывода упорядочить элементы дерева в соответствии с иерархией, уж точно придется воспользоваться рекурсией! Или нет? Давайте разберемся, а заодно решим на SQL пару комбинаторных задач.

Давайте возьмем в качестве примера прочитанный из базы набор записей чего-то вроде справочника сотрудников. Они образуют ориентированное дерево из отделов и работающих в них сотрудников, которое выглядит примерно вот так:
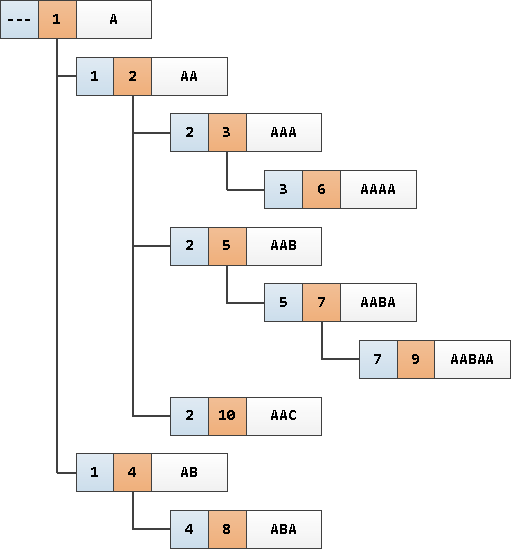
Точнее, это нам хочется, чтобы оно выглядело именно так — дочерний узел под родительским, правильная сортировка «детей» внутри одного предка, красивые отступы… Но база-то нам отдаст записи отсортированными в том порядке, который удобнее ей — скорее всего, по первичному ключу
id:
Давайте все-таки сначала формально определим те правила, которым должен отвечать искомый порядок записей:
- элемент-предок стоит раньше любого из элементов его поддерева
- дочерние элементы внутри одного родительского упорядочиваются по дополнительному прикладному ключу
Второе требование отражает привычные для пользователя паттерны, когда папки внутри одного каталога отображаются отсортированными по названию, а ответы на сообщение в ветке форума — по времени.
Мы, для простоты, возьмем в нашем примере в качестве такого ключа —
data.«Таков путь!»
Собственно, а что мы такое можем сконструировать, чтобы сортировка этого «чего-то» давала нам желаемый результат?
Давайте для каждого элемента дерева вычислим «путь» — цепочку из прикладных ключей всех элементов, которые надо пройти от корня, чтобы его достигнуть:

Но если на каждом шаге такого пути мы сортируем элементы согласно прикладному ключу, то и массивы, составленные из этих ключей, будучи отсортированными, дадут нам искомый порядок записей!
Рекурсивная сортировка
Сначала воспользуемся наиболее традиционным и очевидным способом получения нужного нам результата — рекурсивным запросом:
WITH RECURSIVE src(id, pid, data) AS (
VALUES
(1, NULL, 'A')
, (2, 1, 'AA')
, (3, 2, 'AAA')
, (4, 1, 'AB')
, (5, 2, 'AAB')
, (6, 3, 'AAAA')
, (7, 5, 'AABA')
, (8, 4, 'ABA')
, (9, 7, 'AABAA')
, (10, 2, 'AAC')
)
, T AS (
SELECT
id
, ARRAY[data] path -- инициализируем массив пути корневым элементом
FROM
src
WHERE
pid IS NULL
UNION ALL
SELECT
s.id
, T.path || s.data -- наращиваем путь
FROM
T
JOIN
src s
ON s.pid = T.id
)
SELECT
*
FROM
src
NATURAL JOIN
T
ORDER BY
path; -- сортируем согласно пути id | pid | data | path
----+-----+-------+-----------------------
1 | | A | {A}
2 | 1 | AA | {A,AA}
3 | 2 | AAA | {A,AA,AAA}
6 | 3 | AAAA | {A,AA,AAA,AAAA}
5 | 2 | AAB | {A,AA,AAB}
7 | 5 | AABA | {A,AA,AAB,AABA}
9 | 7 | AABAA | {A,AA,AAB,AABA,AABAA}
10 | 2 | AAC | {A,AA,AAC}
4 | 1 | AB | {A,AB}
8 | 4 | ABA | {A,AB,ABA}
Подключаем комбинаторику
А теперь вернемся к началу статьи и подумаем, как же все-таки для той же самой задачи мы можем создать нерекурсивное решение. В этом нам поможет…
Комбинато́рика (комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка).Сначала решим несколько небольших типовых задач из этой области.
Комбинации
Пусть у нас есть исходный массив
{A,B,C}, все элементы которого уникальны. Получим все комбинации массивов той же длины, состоящие из его элементов:{A,A,A}
{A,A,B}
{A,A,C}
{A,B,A}
{A,B,B}
...
{C,C,B}
{C,C,C}
Достаточно очевидно, что при длине массива
N таких вариантов будет ровно N^N, но как получить их на SQL?Обратим внимание, что каждой комбинации элементов соответствует комбинация позиций этих элементов в исходном массиве, если пронумеровать их с нуля. А каждой такой комбинации — число в N-ричной системе счисления:
3^2 | 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2
3^1 | 0 0 0 1 1 1 2 2 2 0 0 0 1 1 1 2 2 2 0 0 0 1 1 1 2 2 2
3^0 | 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2
=== | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26Решение становится достаточно очевидным:
- генерируем каждое число в диапазоне
0 .. N^N - 1 - раскладываем в N-ричную систему счисления
- берем элемент на соответствующей позиции разложения
SELECT
dst
FROM
-- исходный набор элементов
(VALUES('{A,B,C}'::varchar[])) data(src)
-- кэшируем размер набора
, LATERAL array_length(src, 1) n
-- кэшируем границу интервала
, LATERAL (SELECT (n ^ n)::bigint l) X
-- генерируем все числа на интервале
, LATERAL generate_series(0, l - 1) num
-- формируем разложение числа в N-ричной системе
, LATERAL (
SELECT
array_agg((num % (n ^ (pos + 1))::bigint) / (n ^ pos)::bigint ORDER BY pos DESC) num_n
FROM
generate_series(0, n - 1) pos
) Y
-- собираем элементы согласно "цифрам"
, LATERAL (
SELECT
array_agg(src[num_n[pos] + 1]) dst
FROM
generate_subscripts(num_n, 1) pos
) Z;
Перестановки
Но в оригинальном наборе у нас каждый элемент был уникален, а в полученных нами комбинациях это правило не соблюдается. Исправим, получив все возможные перестановки. Для этого отфильтруем из
num_n только те, где встречаются все «цифры»:JOIN LATERAL(
SELECT
count(DISTINCT unnest) = n cond
FROM
unnest(num_n)
) flt
ON cond
Полный вариант запроса
SELECT
dst
FROM
-- исходный набор элементов
(VALUES('{A,B,C}'::varchar[])) data(src)
-- кэшируем размер набора
, LATERAL array_length(src, 1) n
-- кэшируем границу интервала
, LATERAL (SELECT (n ^ n)::bigint l) X
-- генерируем все числа на интервале
, LATERAL generate_series(0, l - 1) num
-- формируем разложение числа в N-ричной системе
, LATERAL (
SELECT
array_agg((num % (n ^ (pos + 1))::bigint) / (n ^ pos)::bigint ORDER BY pos DESC) num_n
FROM
generate_series(0, n - 1) pos
) Y
-- фильтруем комбинации с неполным набором "цифр"
JOIN LATERAL(
SELECT
count(DISTINCT unnest) = n cond
FROM
unnest(num_n)
) flt
ON cond
-- собираем элементы согласно "цифрам"
, LATERAL (
SELECT
array_agg(src[num_n[pos] + 1]) dst
FROM
generate_subscripts(num_n, 1) pos
) Z;Это дает нам все возможные перестановки исходного набора:
{A,B,C}
{A,C,B}
{B,A,C}
{B,C,A}
{C,A,B}
{C,B,A}Можно использовать и «неэкспоненциальный» алгоритм на основе «тасований», работающий за
O(N*N!), но его реализация явно выходит за рамки данной статьи.Подмножества
Сделаем шаг чуть в сторону и научимся генерировать все подмножества исходного набора с сохранением порядка. То есть для нашего набора
{A,B,C} должно получиться вот это:{}
{A}
{B}
{A,B}
{C}
{A,C}
{B,C}
{A,B,C}В принципе, задача очень близка к первой решенной нами. Только вместо позиции двоичная «цифра» означает отсутствие или наличие соответствующего элемента в результирующем наборе:
2^2 | 0 0 0 0 1 1 1 1
2^1 | 0 0 1 1 0 0 1 1
2^0 | 0 1 0 1 0 1 0 1
=== | 0 1 2 3 4 5 6 7Поскольку двоичная арифметика представлена в компьютерах гораздо эффективнее, мы можем воспользоваться функциями работы с битовыми строками:
-- кэшируем разложение числа в двоичной системе
, LATERAL (SELECT num::bit(64) num_n) Y
-- собираем элементы согласно "цифрам"
, LATERAL (
SELECT
coalesce(array_agg(src[i]) FILTER(WHERE get_bit(num_n, 64 - i) = 1), '{}') dst
FROM
generate_series(1, n) i
) Z
Полный вариант запроса
SELECT
dst
FROM
-- исходный набор элементов
(VALUES('{A,B,C}'::varchar[])) data(src)
-- кэшируем размер набора
, LATERAL array_length(src, 1) n
-- кэшируем границу интервала
, LATERAL (SELECT (2 ^ n)::bigint l) X
-- генерируем все числа на интервале
, LATERAL generate_series(0, l - 1) num
-- кэшируем разложение числа в двоичной системе
, LATERAL (SELECT num::bit(64) num_n) Y
-- собираем элементы согласно "цифрам"
, LATERAL (
SELECT
coalesce(array_agg(src[i]) FILTER(WHERE get_bit(num_n, 64 - i) = 1), '{}') dst
FROM
generate_series(1, n) i
) Z;Иерархия — без рекурсии!
Теперь, вооруженные всеми приведенными выше алгоритмами, попробуем найти решение нашей задачи сначала в общем виде, а затем разберем один из типичных частных случаев.
Пути-дороги
Для начала воспользуемся тем фактом, что в качестве элементов пути, который идентифицирует конкретную запись, можно использовать уникальные ключи промежуточных записей — в нашем случае это
id.Но сортировать по такому пути, конечно, будет некорректно — поэтому для дальнейшей сортировки превратим
id записей в соответствующее значение data, которое использовали в первом варианте.Дано: газовая плита, чайник. Задача: вскипятить воду.Но как найти путь до каждого из элементов без рекурсии? Вот здесь нам и пригодятся алгоритмы выше.
Физик: Зажечь плиту, наполнить чайник водой и поставить на плиту, ждать.
Математик: Аналогично.
Дано: зажженная газовая плита, наполненный водой чайник. Задача: вскипятить воду.
Физик: Поставить чайник на плиту, ждать.
Математик: Выливаем воду из чайника на плиту. Огонь погас, чайник пуст, задача сведена к предыдущей.
© Народный анекдот
Корректный путь от корня до конкретного элемента обладает следующими свойствами:
- Правило #1: начинается и заканчивается нужными нам элементами
path[1] = root AND path[array_length(path, 1)] = id - Правило #2: предок каждого элемента, кроме корневого, так же присутствует в наборе
pid = ANY(path) OR pid = root - Правило #3: из всех таких наборов искомый — самой маленькой длины
Иначе дляid=3наборы{1,2,3}и{1,2,3,4}окажутся равноподходящими, поскольку предокid=4 (pid=1)тоже присутствует. - Правило #4: предок каждого элемента стоит ровно в предыдущей позиции
pid = path[pos - 1]
Итак, намечаем план действий:
- генерируем все подмножества элементов, исключая
rootиid, формируя «тело» пути по правилу #1 - проверяем выполнение правила #2
- выбираем, согласно правилу #3, самый короткий набор
- генерируем все перестановки его элементов
- проверяем выполнение правила #4
- что осталось — искомый «путь»
Полный вариант запроса, смотреть с осторожностью
Я вас предупредил… [источник картинки]

WITH src(id, pid, data) AS (
VALUES
(1, NULL, 'A')
, (2, 1, 'AA')
, (3, 2, 'AAA')
, (4, 1, 'AB')
, (5, 2, 'AAB')
, (6, 3, 'AAAA')
, (7, 5, 'AABA')
, (8, 4, 'ABA')
, (9, 7, 'AABAA')
, (10, 2, 'AAC')
)
-- кэшируем ID корневого элемента
, root AS (
SELECT
id
FROM
src
WHERE
pid IS NULL
LIMIT 1
)
-- формируем уже известные пути и предварительные наборы
, preset AS (
SELECT
*
, CASE
-- для корневого элемента путь состоит только из него самого
WHEN pid IS NULL THEN ARRAY[id]
-- для ссылающегося на корневой - из пары
WHEN pid = (TABLE root) THEN ARRAY[pid, id]
END prepath
, CASE
WHEN pid IS NULL THEN NULL
WHEN pid = (TABLE root) THEN NULL
-- все ID, кроме корневого и собственного - EXCLUDE CURRENT ROW
ELSE array_agg(id) FILTER(WHERE pid IS NOT NULL) OVER(ROWS BETWEEN UNBOUNDED PRECEDING AND UNBOUNDED FOLLOWING EXCLUDE CURRENT ROW)
END preset
FROM
src
)
-- формируем "переборные" пути
, prepath AS (
SELECT
id
, prepath
FROM
-- отбираем только элементы, чей путь еще не определили
(
SELECT
id
, pid
, preset src -- комбинируемый набор
FROM
preset
WHERE
prepath IS NULL
) data
-- подмножества
, LATERAL (
SELECT
dst pathset
FROM
-- кэшируем размер набора
LATERAL array_length(src, 1) n
-- кэшируем границу интервала
, LATERAL (SELECT (2 ^ n)::bigint l) X
-- генерируем все числа на интервале
, LATERAL generate_series(1, l - 1) num -- тут можно с 1, поскольку пустой набор нас заведомо не интересует
-- кэшируем разложение числа в двоичной системе
, LATERAL (SELECT num::bit(64) num_n) Y
-- собираем элементы согласно "цифрам"
, LATERAL (
SELECT
coalesce(array_agg(src[i]) FILTER(WHERE get_bit(num_n, 64 - i) = 1), '{}') || data.id dst
FROM
generate_series(1, n) i
) Z
-- проверяем наличие предка в наборе
, LATERAL (
SELECT
NULL
FROM
(
SELECT
(SELECT pid FROM src WHERE id = dst[i] LIMIT 1) _pid
FROM
generate_subscripts(dst, 1) i
) T
HAVING
bool_and(_pid = (TABLE root) OR _pid = ANY(dst))
) rule2
-- отбираем первый подходящий минимальной длины
ORDER BY
array_length(dst, 1) -- rule3
LIMIT 1
) X
-- перестановки
, LATERAL (
SELECT
dst prepath
FROM
-- исходный набор элементов
(SELECT pathset) data(src)
-- кэшируем размер набора
, LATERAL array_length(src, 1) n
-- кэшируем границу интервала
, LATERAL (SELECT (n ^ n)::bigint l) X
-- генерируем все числа на интервале
, LATERAL generate_series(0, l - 1) num
-- формируем разложение числа в N-ричной системе
, LATERAL (
SELECT
array_agg((num % (n ^ (pos + 1))::bigint) / (n ^ pos)::bigint ORDER BY pos DESC) num_n
FROM
generate_series(0, n - 1) pos
) Y
-- фильтруем комбинации с неполным набором "цифр"
JOIN LATERAL(
SELECT
count(DISTINCT unnest) = n cond
FROM
unnest(num_n)
) flt
ON cond
-- собираем элементы согласно "цифрам"
, LATERAL (
SELECT
array_agg(src[num_n[pos] + 1]) dst
FROM
generate_subscripts(num_n, 1) pos
) Z
-- проверяем наличие предка в предыдущей позиции
, LATERAL (
SELECT
NULL
FROM
(
SELECT
(SELECT pid FROM src WHERE id = dst[i] LIMIT 1) _pid
, i
FROM
generate_subscripts(dst, 1) i
) T
HAVING
bool_and((i = 1 AND _pid = (TABLE root)) OR _pid = dst[i - 1])
) rule4
) Y
)
SELECT
src.*
-- восстанавливаем "путь" из прикладных ключей
, (
SELECT
array_agg(data ORDER BY i)
FROM
coalesce(X.prepath, ARRAY[(TABLE root)] || Y.prepath) p -- помним о необходимости добавить "корень"
, LATERAL generate_subscripts(p, 1) i
, LATERAL (
SELECT
data
FROM
src
WHERE
id = p[i]
LIMIT 1
) T
) path
FROM
src
LEFT JOIN
preset X
USING(id)
LEFT JOIN
prepath Y
USING(id)
ORDER BY
path;А попроще — можно?..
Можно и попроще, если заранее известно, что порядок «детей» внутри одного «родителя» определяется некоторым сквозным ключом. Например, это может быть некоторый монотонно возрастающий timestamp сообщений в ветке форума или, как в нашем случае, первичный ключ типа
serial (id).В таком случае, мы уже точно знаем порядок следования идентификаторов записей в нужном нам пути — он совпадает с общей сортировкой по этому ключу. И нам надо только выкинуть лишние id из списка всех предстоящих:
WITH src(id, pid, data) AS (
VALUES
(1, NULL, 'A')
, (2, 1, 'AA')
, (3, 2, 'AAA')
, (4, 1, 'AB')
, (5, 2, 'AAB')
, (6, 3, 'AAAA')
, (7, 5, 'AABA')
, (8, 4, 'ABA')
, (9, 7, 'AABAA')
, (10, 2, 'AAC')
)
-- кэшируем ID корневого элемента
, root AS (
SELECT
id
FROM
src
WHERE
pid IS NULL
LIMIT 1
)
-- собираем все предстоящие id в массив для текущего
, prepath AS (
SELECT
id
, pid
, array_agg(id) OVER(ORDER BY id /*!!! сортировка по тому самому ключу*/ ROWS UNBOUNDED PRECEDING EXCLUDE CURRENT ROW) src
FROM
src
WHERE
pid IS NOT NULL
)
-- находим пути
, pre AS (
SELECT
id
, path
FROM
prepath
-- подмножества
, LATERAL (
SELECT
dst path
FROM
-- кэшируем размер набора
LATERAL array_length(src, 1) n
-- кэшируем границу интервала
, LATERAL (SELECT (2 ^ n)::bigint l) X
-- генерируем все числа на интервале
, LATERAL generate_series(0, l - 1) num
-- кэшируем разложение числа в двоичной системе
, LATERAL (SELECT num::bit(64) num_n) Y
-- собираем элементы согласно "цифрам"
, LATERAL (
SELECT
coalesce(array_agg(src[i]) FILTER(WHERE get_bit(num_n, 64 - i) = 1), '{}') || id dst
FROM
generate_series(1, n) i
) Z
-- проверяем наличие предка в предыдущей позиции
, LATERAL (
SELECT
NULL
FROM
(
SELECT
(SELECT pid FROM src WHERE id = dst[i] LIMIT 1) _pid
, i
FROM
generate_subscripts(dst, 1) i
) T
HAVING
bool_and((i = 1 AND _pid = (TABLE root)) OR (i > 1 AND _pid = dst[i - 1]))
) rule4
) X
)
SELECT
src.*
-- восстанавливаем "путь" из прикладных ключей
, (
SELECT
array_agg(data ORDER BY i)
FROM
(
SELECT
CASE
-- для корневого элемента путь состоит только из него самого
WHEN pid IS NULL THEN ARRAY[id]
-- для ссылающегося на корневой - из пары
WHEN pid = (TABLE root) THEN ARRAY[pid, id]
ELSE ARRAY[(TABLE root)] || pre.path
END p -- помним о необходимости добавить "корень"
) p
, LATERAL generate_subscripts(p, 1) i
, LATERAL (
SELECT
data
FROM
src
WHERE
id = p[i]
LIMIT 1
) T
) path
FROM
src
LEFT JOIN
pre
USING(id)
ORDER BY
path;Понятно, что производительность таких «экспоненциальных» решений не особо велика и применять «в бою» надо с большой осторожностью, но как гимнастика для ума — вполне.