Комментарии 4
Статья интересная, но перевод подвёл... Можно ссылку на оригинал?
0
черпал инфу из исследования в Science Advances
www.science.org/doi/10.1126/sciadv.abk0468
www.science.org/doi/10.1126/sciadv.abk0468
+1
То есть чтобы описать линию, мы должны знать о понятии длины, квадрат — длины и ширины, а, чтобы описать куб, нам должно быть известно понятие высотыОбобщением для всех этих понятий служит понятие меры (грубо говоря — объема) множества, точнее, длины в одномерном пространстве, площади в двумерном и объема в трехмерном. Строгое определение меры приводит к понятиям измеримых и неизмеримых множеств, вторые могут служить основой для всяких странных вещей вроде парадокса Банаха-Тарского.
Кроме того, уже довольно давно известны множества, размерность которых — нецелая. Для таких множеств их размерность определяется как предел объема кубиков, покрывающих множество, при стремящемся к нулю объему кубика. Существуют и другие определения размерности, общим для них является то, что для простого тела мера-объем, вычисляемая в соответствии с определением, будет обычным объемом. Вот пример множества нецелой размерности — аттрактор Тома́, множество, к которому стремится эта трехмерная траектория, имеет размерность ~ 2.809
Аттрактор Тома

Другой пример множества с нецелой размерностью — фракталы.
+2
Поправлю сам себя — разумеется, размерность — это не объем, просто для покрытия нужно выбирать кубики того эвклидова пространства, в котором существует исходное множество. Если оно живет в трехмерном пространстве, кубики должны быть трехмерными. Число трехмерных кубиков со стороной  , необходимое для покрытия объема в трехмерном пространстве, пропорционально
, необходимое для покрытия объема в трехмерном пространстве, пропорционально 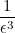 , поэтому размерность множества можно определить как
, поэтому размерность множества можно определить как 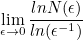 , где N — минимальное кол-во кубиков, необходимое для покрытия множества.
, где N — минимальное кол-во кубиков, необходимое для покрытия множества.
Подробнее см. Лоскутов, Михайлов, «Введение в синергетику»
 , необходимое для покрытия объема в трехмерном пространстве, пропорционально
, необходимое для покрытия объема в трехмерном пространстве, пропорционально  , поэтому размерность множества можно определить как
, поэтому размерность множества можно определить как  , где N — минимальное кол-во кубиков, необходимое для покрытия множества.
, где N — минимальное кол-во кубиков, необходимое для покрытия множества.Подробнее см. Лоскутов, Михайлов, «Введение в синергетику»
+1
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Синтетические измерения. За 4D-реальностью