
Когда два года назад Нэтан Кляйн поступил в аспирантуру, его руководители предложили ему скромный план: совместную работу над одной из самых известных и давних задач теоретической информатики.
Они посчитали, что даже если Нэтану не удастся её решить, то в процессе работы он многому научится. Он согласился на эту идею. «Я не знал, что мне нужно бояться», — говорит Кляйн. «Я был всего лишь начинающим аспирантом, поэтому не понимал сложность этой задачи».
В опубликованной в июле статье Кляйн и его руководители из Университета Вашингтона Анна Карлин и Шаян Овеис-Гаран наконец-то достигли цели, к которой учёные стремились почти полвека: они нашли улучшенный способ поиска аппроксимированных значений задачи коммивояжёра.
Эта задача оптимизации по поиску кратчайшего (или наименее затратного) маршрута по списку городов применяется во многих областях, от секвенирования ДНК до логистики совместного использования автомобилей (райдшеринга). На протяжении десятилетий она вдохновляла учёных на самые фундаментальные достижения в информатике, помогая подчеркнуть мощь дисциплин наподобие линейного программирования. Однако исследователям ещё предстоит полностью изучить все её возможности, и они к этому стремятся.
Как с любовью говорит ведущий специалист по вычислительной сложности Кристос Пападимитриу, задача коммивояжёра — «это не задача, а привязанность».
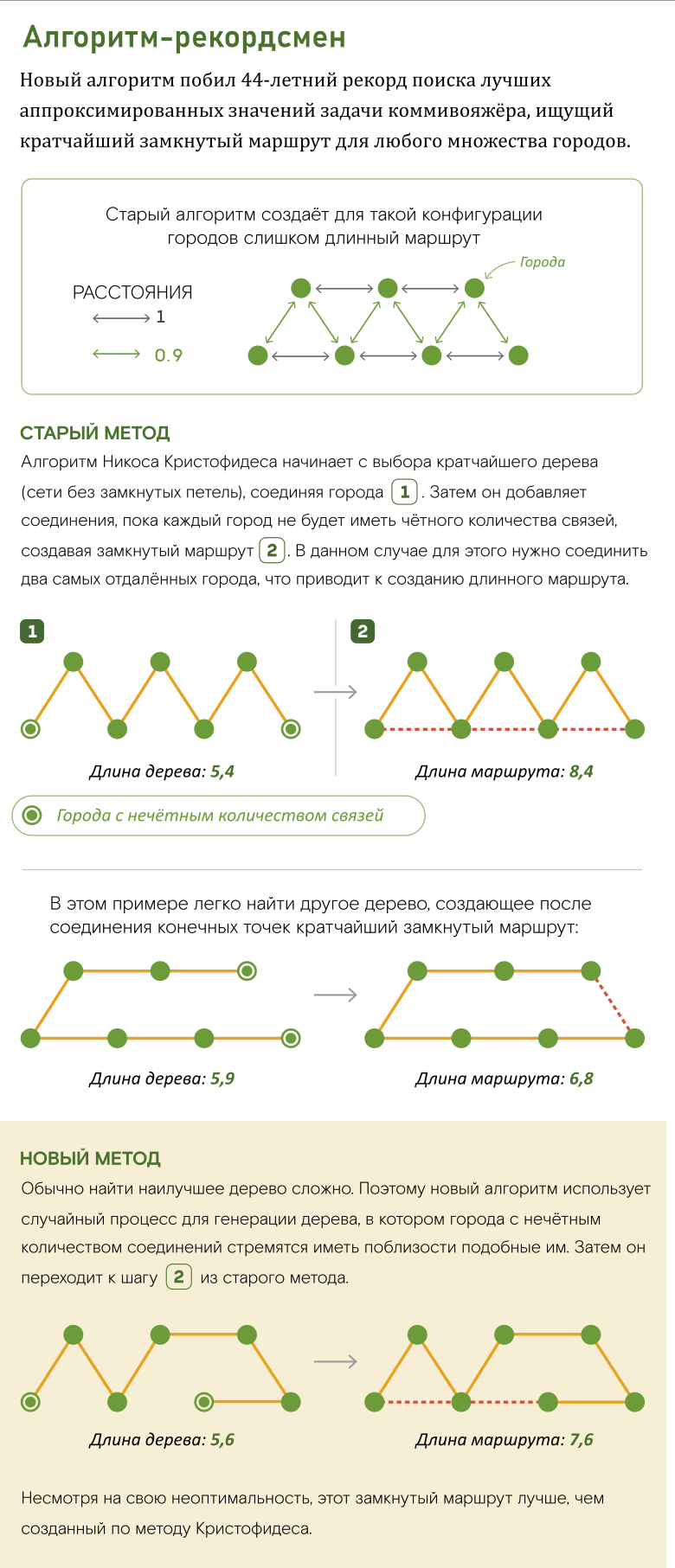
Большинство учёных-информатиков считает, что не существует алгоритма для эффективного поиска наилучших решений для всех возможных сочетаний городов. Однако в 1976 году Никос Кристофидес придумал алгоритм, эффективно находящий аппроксимированные значения — маршруты, которые не более чем на 50% длиннее наиболее оптимального маршрута. В то время учёные полагали, что вскоре кто-нибудь усовершенствует простой алгоритм Кристофидеса и приблизится к истинному решению. Однако ожидаемый прогресс так и не произошёл.
«Множество людей потратило бесчисленное количество часов на улучшение этого результата», — говорит Амин Сабери из Стэнфордского университета.
Сегодня Карлин, Кляйн и Овеис-Гаран доказали, что придуманный десять лет назад алгоритм улучшает результат алгоритма Кристофидеса (50%), хоть ему и удалось снизить этот показатель всего на 0,2 миллиардных триллионных триллионных процента (0,2-31%). Тем не менее, это микроскопическое улучшение разрушает и теоретический, и психологический барьер. Исследователи надеются, что это откроет возможности для дальнейшего совершенствования.

Аспирант Университета Вашингтона Нэтан Кляйн (слева) и его руководители Анна Карлин и Шаян Овеис-Гаран.
«К этому результату я стремился в течение всей своей карьеры», — говорит Дэвид Уильямсон из Корнеллский университет, изучавший задачу коммивояжёра с 1980-х годов.
Задача коммивояжёра — одна из немногих фундаментальных задач, к которой специалисты по информатике снова и снова обращаются для проверки пределов эффективных вычислений. Новый результат «стал первым шагом к демонстрации того, что перспективы эффективных вычислений на самом деле лучше, чем мы думали», — поясняет Уильямсон.
Дробный прогресс
Несмотря на то, что, скорее всего, не существует эффективного метода нахождения кратчайшего маршрута, мы можем найти нечто почти столь же полезное: кратчайшее дерево, соединяющее все города, то есть сеть связей (или «рёбер») без замкнутых петель. Алгоритм Кристофидеса использует это дерево в качестве основы для движения по пути, добавляя новые рёбра, чтобы преобразовать его в замкнутый маршрут.
Любой замкнутый маршрут должен иметь чётное количество рёбер в каждом из городов, потому что за каждым прибытием следует отъезд. Оказывается, обратное тоже верно — если каждый город в сети имеет чётное количество соединений, то рёбра сети должны образовывать замкнутый маршрут.
Кратчайшее дерево, соединяющее все города, не имеет этого свойства чётности, потому что любой город в конце ветви содержит только одно соединение с другим городом. Поэтому чтобы превратить кратчайшее дерево в замкнутый маршрут, Кристофидес (покинувший нас в прошлом году) обнаружил наилучший способ соединения пар городов, имеющих нечётное количество рёбер. Потом он доказал, что получившийся маршрут никогда не будет более чем на 50% длиннее самого оптимального маршрута.
При этом он вывел самый знаменитый в теоретической информатике алгоритм аппроксимации, который обычно становится первым примером во всех учебниках и курсах.
«Все знают этот простой алгоритм», — говорит Аланта Ньюман из Гренобльского альпийского университета и Национального центра научных исследований Франции. А если вы знаете его, то, по словам Аланты, «знаете и последние достижения в этой науке». По крайней мере, так было до июля этого года.
Компьютерные учёные давно подозревали, что существует алгоритм аппроксимации, превосходящий алгоритм Кристофидеса. В конце концов, его простой и интуитивно понятный алгоритм не всегда является таким уж эффективным способом построения маршрута коммивояжёра, ведь кратчайшее дерево, соединяющее города, может быть не лучшей основой. Например, если это дерево имеет множество ветвей, то каждый город в конце ветви нужно будет соединить с другим городом, потенциально создавая множество затратных новых связей.
В 2010 году Овеис-Гаран, Сабери и Мохит Сингх из Технологического института Джорджии начали размышлять над тем, можно ли усовершенствовать алгоритм Кристофидеса, выбирая не кратчайшее дерево, соединяющее все города, а случайное дерево из тщательно выбранного набора. Они вдохновлялись альтернативной версией задачи коммивояжёра, в которой можно путешествовать по комбинации путей — допустим, до Денвера можно добраться по 3/4 маршрута от Чикаго до Денвера плюс по 1/4 маршрута от Лос-Анджелеса до Денвера.
В отличие от стандартной задачи коммивояжёра, эту дробную задачу можно решить эффективно. И хотя дробные пути не имеют физического смысла, компьютерные учёные давно считали, что наилучшие дробные маршруты должны быть приблизительным намёком о контурах хороших обычных маршрутов.
Для создания своего алгоритма Овеис-Гаран, Сабери и Сингх определили случайный процесс, выбиравший соединяющее все города дерево, таким образом, чтобы вероятность нахождения ребра в этом дереве равнялась дроби ребра в наилучшем дробном маршруте. Существует множество таких случайных процессов, поэтому исследователи выбрали тот из них, которые создавал деревья со множеством чётно соединённых городов. После того, как этот случайный процесс выдавал на выходе конкретное дерево, алгоритм исследователей вставлял его в схему Кристофидеса для сопоставления городов с нечётным количеством рёбер, чтобы преобразовать его в замкнутый маршрут.
Этот метод показался многообещающим не только трём исследователям, но и другим специалистам по информатике. «Интуитивно это понять легко», — писал Ола Свенссон из швейцарской Федеральной политехнической школы Лозанны. Однако «доказательство оказалось совершенно другой проблемой».
Однако на следующий год Овеис-Гаран, Сабери и Сингх смогли доказать, что их алгоритм побеждает алгоритм Кристофидеса в «графических» задачах коммивояжёра — в тех, где расстояния между городами представлены сеткой (не обязательно с включением всех соединений), в которой каждое ребро имеет одинаковую длину. Однако исследователям не удалось разобраться, как расширить их результат на обобщённую задачу коммивояжёра, в которой некоторые рёбра могут быть значительно длиннее других.
«Если бы нам пришлось добавить в соединение очень затратное ребро, то всё бы, по сути, развалилось бы», — признаёт Карлин.
Возврат назад
Тем не менее, после этой совместной работы Овеис-Гарана не покидало ощущение, что их алгоритм должен победить алгоритм Кристофидеса для общей задачи коммивояжёра. «У меня никогда не было в этом сомнений», — говорит он.
В течение последующих лет Овеис-Гаран продолжал обдумывать задачу. Он заподозрил, что нужные ему инструменты могут найтись в математической дисциплине под названием «геометрия многочленов», малоизвестной в мире теоретических компьютерных наук. Поэтому когда два года назад Карлин обратилась к нему с предложением вместе стать руководителями блестящего нового аспиранта Нэтана Кляйна, который профилировался в двух дисциплинах — математике и виолончели, он сказал: «Хорошо, давайте попробуем, у меня есть интересная задача».
Карлин думала, что, по крайней мере, это станет интересной возможностью больше узнать о геометрии многочленов. «На самом деле я не думала, что мы сможем решить эту задачу», — признаётся она.
Вместе с Овеис-Гараном они сразу же погрузили Кляйна в процесс исследований информатики. Сам Овеис-Гаран съел собаку на задаче коммивояжёра, когда в 2010 году бы аспирантом. Два руководителя пришли к соглашению о преимуществах возложения трудных задач на аспирантов, особенно в первые пару лет, когда на них ещё не давят и не требуют результатов.
Троица приступила к активному сотрудничеству. «Это всё, о чём я думал в течение двух лет», — говорит Кляйн.
Первый год они потратили на решение упрощённой версии задачи, чтобы понять сложности, с которыми столкнулись. Но даже после завершения этой работы решение обобщённой задачи, по словам Кляйна, казалось слишком тяжёлой ношей.
Тем не менее, они освоили свой инструментарий, в частности, геометрию многочленов. Многочлен — это сочетание членов, составленных из чисел и возведённых в степень переменных, например, 3x2y + 8xz7. Для изучения задачи коммивояжёра исследователи свели карту городов к многочлену, имевшему по одной переменной для каждого ребра между городами, и по одному члену для каждого дерева, способного соединить все города. Затем числовые коэффициенты добавляли веса этим членам, чтобы отразить значение каждого ребра в дробном решении задачи коммивояжёра.
Исследователи выяснили, что обнаруженный ими многочлен обладает желанным свойством «вещественной устойчивости», означающей, что комплексные числа, при которых значение многочлена равно нулю, никогда не находятся в верхней половине комплексной плоскости. Удобство свойства вещественной устойчивости заключается в том, что оно действует даже при различных изменениях, вносимых в многочлен. То есть, если, например, исследователи хотели сосредоточиться на конкретных городах, то они могли использовать для обозначения всех ведущих в город различных рёбер одну переменную, а также присвоить переменным всех рёбер, которые им были не важны, значение 1. В процессе манипуляций с этими упрощёнными многочленами результаты манипуляций по-прежнему обладали вещественной устойчивостью, что позволяло применять широкий ассортимент методик.
Такой подход позволил исследователям разобраться с вопросами типа «как часто алгоритм будет вынужден соединять два отдалённых города?». В своём анализе почти из 80 страниц им удалось показать, что их алгоритм побеждает алгоритм Кристофидеса в обобщённой задаче коммивояжёра (статья ещё готовится к рецензированию, но специалисты уверены, что она верна). После завершения статьи Овеис-Гаран сразу же отправил письмо своему старому научному руководителю Сабери. «Похоже, я наконец могу закончить аспирантуру», — пошутил он.

Амин Сабери из Стэнфордского университета (слева) и Мохит Сингх из Технологического университета Джорджии.
Хотя реализованное исследователями улучшение исчезающе мало, учёные-информатики надеются, что этот прорыв стимулирует быстрый дальнейший прогресс. Именно так и произошло в 2011 году, когда Овеис-Гаран, Сабери и Сингх разобрались с графическим примером. В течение года другие исследователи придумали радикально иные алгоритмы, значительно улучшившие показатель аппроксимации для графического примера, понизив его до 40% по сравнению с 50% Кристофидеса.
«Когда они объявили о своём результате с графическим примером, мы поняли, что такое возможно. Это заставило нас работать над этой задачей», — говорит Свенссон — один из учёных, совершивших дальнейший прогресс с этим примером. Он годами пытался победить алгоритм Кристофидеса для обобщённой задачи коммивояжёра. «Теперь, когда я знаю, что это возможно, я попробую снова», — заявляет он.
За многие десятилетия задача коммивояжёра стала причиной роста известности множества новых методик. Овеис-Гаран надеется, что теперь она сыграет свою роль в популярности геометрии многочленов, страстным евангелистом которой он стал. За десятилетие, прошедшее после того, как он узнал об этой методике, она помогла ему доказать широкий спектр теорем. Этот инструмент «обусловил продолжение всей моей дальнейшей карьеры», — признаёт он.
Ньюман говорит, что новый результат решения задачи коммивояжёра подчёркивает мощь этого подхода. «Он определённо стал источником вдохновения, достойный более внимательного изучения».
Кляйну теперь нужно найти задачу, которая станет новой причиной его одержимости. «Мне немного грустно, что я потерял эту задачу, ведь я построил в голове так много структур, а теперь они как будто пропали», — делится он. Но он и мечтать не мог о более плодотворном знакомстве с исследованиями в сфере информатики. «Я чувствую, что мы немного раздвинули границы неизвестного нам».
На правах рекламы
Вдсина предлагает виртуальные серверы на Linux или Windows. Используем исключительно брендовое оборудование, лучшую в своём роде панель управления серверами собственной разработки и одни из лучших дата-центров в России и ЕС. Поспешите заказать!
