Алгоритмы машинного обучение сегодня нужны во всех ключевых бизнес-процессах любого финансового института. Все больше решений принимается с применением моделей, а значит контроль их качества в условиях постоянно меняющегося рынка — ключевая задача финансовой организации.
Одна из проблем мониторинга моделей — существенный временной разрыв между датой прогноза и наблюдением фактического значения целевой переменной. Под катом мы расскажем про новые методы, которые прогнозируют снижение предсказательной способности модели.

Моделирование в банке не разовое упражнение, а сложный процесс. Важно как можно раньше идентифицировать снижение качества модели, особенно во времена резко меняющихся экономических условий.
Для «вызревания» многих целевых переменных в прикладных банковских задачах требуются существенные временные периоды. Например, в задачах кредитного скоринга временной горизонт прогнозирования события дефолта составляет 12 месяцев. То есть оценить качество работы, сравнив прогнозные значения вероятностей дефолта с фактически реализовавшимися дефолтами, мы можем только по состоянию на год назад.
«Классические» подходы к снижению модельных рисков базируются на такой гипотезе: существенные отклонения в распределении входных факторов модели могут сигнализировать о нерепрезентативности разработанной модели для текущего входного потока. Чтобы контролировать стабильность факторов модели, в большинстве случаев используют следующие статистические метрики:
У «классических» подходов есть существенные недостатки. Главный из них — контроль стабильности маржинальных (одномерных) распределений факторов, а не совместного (многомерного) распределения, на котором фактически базируется модель. Например, в модели кредитного скоринга могут использоваться факторы возраста и дохода. Если смотреть на факторы по отдельности, возрастная структура и структура доходов входного потока могут почти не меняться. При этом доход может перераспределиться от более возрастных клиентов к более молодым. В результате «классический» подход к мониторингу не выявит изменений, а модель будет в основном применяться на тех участках распределения входного потока, для которых было относительно мало наблюдений в выборке для обучения, следовательно, ошибка прогнозирования может значимо вырасти.
Другими недостатками «классического» подхода является единообразность и неинтуитивность устанавливаемых порогов для мониторинга, а также отсутствие связи устанавливаемых порогов мониторинга и целевой переменной модели.
В подходе MPP (Model Performance Predictor) мы хотим, чтобы модель следила за моделью. И задача следящей модели — предсказывать, как будет ошибаться первая модель в своем прогнозе.
Возможная схема обучения MPP приведена на рисунке ниже.
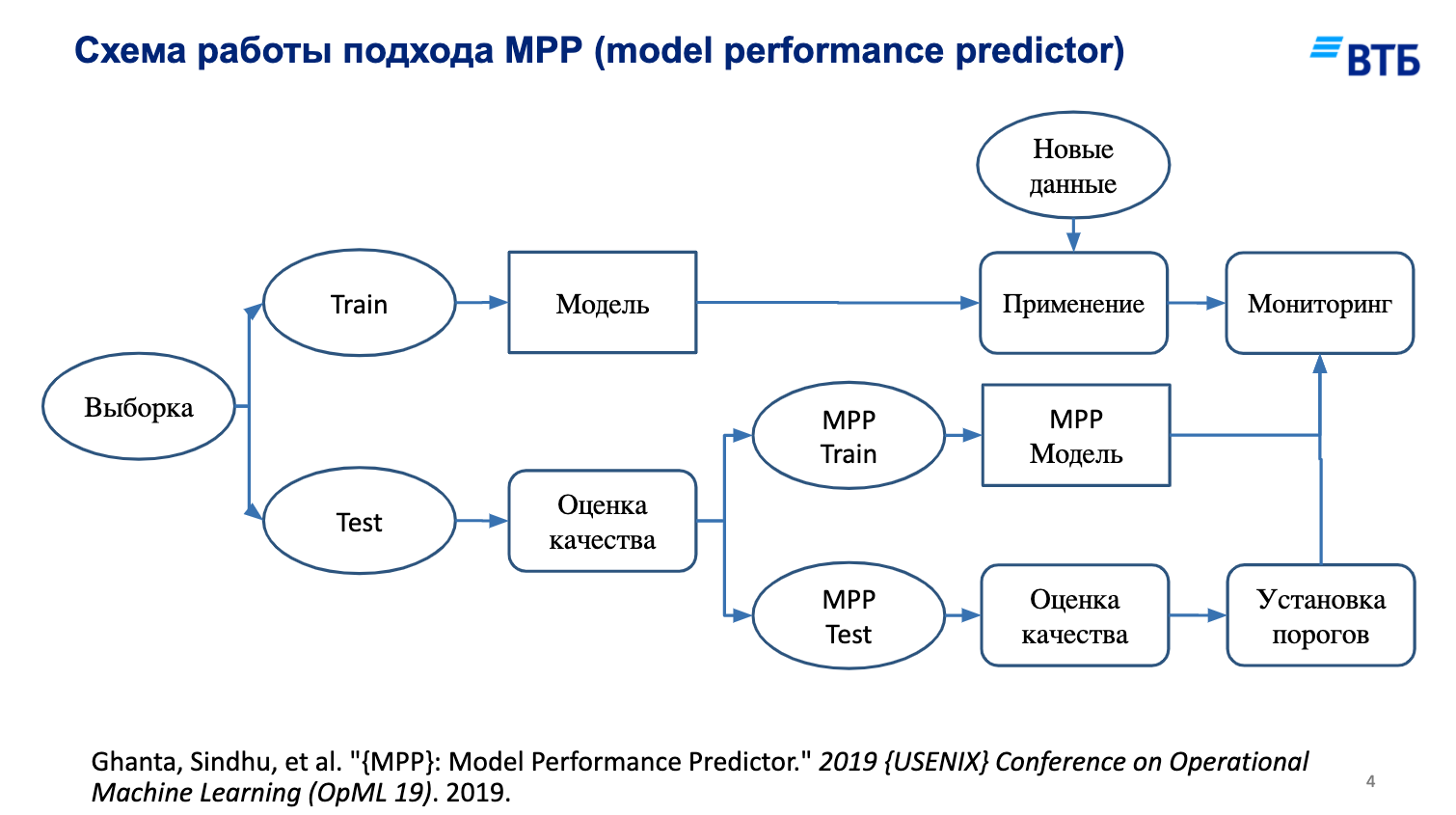
Изначально мы делим выборку на test/train. На train выборке мы применяем стандартные ML pipeline без изменений, а вот в части test происходит вся магия: после подсчета метрик качества на test мы разбиваем эту часть еще на две — MPP train и MPP test — и используем для тренировки в качестве целевой метрики метрику ошибки изначальной модели. В таком контексте определение порогов тоже может быть параметром, который мы оцениваем по данным.
То есть первая модель предсказывает результат, а вторая показывает, насколько первая модель ошибается в своем прогнозе.
Заметим, что данный процесс — это не стекинг, как может изначально показаться, потому что выборки разные: MPP модель обучается на test’е.
И еще данный метод «честнее», чем доверительные интервалы: MPP строится на test’е, в то время как доверительный интервал оценивается на исходных тренировочных данных.
Особенно интересен этот подход, если data scientist ограничен трактуемым классом моделей при разработке. MPP-подход полностью развязывает ему руки при контроле данных моделей, а значит, позволяет использовать весь арсенал продвинутых методов для любой задачи.
Как насчет нарушения «No free lunch theorem»? С точки зрения теории машинного обучения, MPP-подход дает преимущества за счет того, что тестовая выборка используется на все 100% и для валидации модели, и для обучения/проверки модели MPP.
Разберем основные плюсы подхода чуть более формально:
Недостаток в том, что это создает дополнительные сложности и затраты для разработки и внедрения одновременно двух моделей.
В демонстрационных целях построена простая линейная модель прогноза среднего за 10 торговых дней значения индекса МосБиржи MOEX (train: 06.2010-06.2015).
Демонстрационная модель построена на открытых данных, поскольку мы не можем раскрывать реальные данные Банка. Однако, контроль ошибки модели чрезвычайно важен в самых ключевых бизнес-процессах банка, например, в кредитном скоринге, который характеризуется большими временными лагами между наблюдением целевой переменной и прогнозом.
График демонстрирует работу модели на out-of-time выборке, ошибка (error) была использована для обучения модели MPP (период с 01.2020 был использован как out-of-sample для MPP-модели):

На графике видно, как меняется парадигма: с COVID-19 не просто изменяются предсказания, но еще больше изменяются ошибки модели. Это сразу говорит о том, что модель, обученная на предыдущих исторических данных, не отражает текущую ситуацию.
На данных об ошибке первичной модели была обучена нейронная сеть:

Модель не смогла предсказать глубину стресса и направление изменения ошибки, но просигнализировала о смене рыночной конъюнктуры, подняв прогноз ошибки до исторических максимумов.
Более тщательный fine-tuning модели и включение в выборку для обучения периодов исторического стресса потенциально должны улучшить чувствительность MPP-подхода (эти работы не были выполнены, т. к. задача исключительно демонстрационная).
Пробитие порогов в мониторинге может вести к различным управленческим решениям — от долгосрочных (перестроение модели) до моментальных (изменение порогов модельной отсечки при принятии автоматических решений).
Тестовое использование MPP-подхода выявило ряд вопросов:
Вопрос о том, как эффективно применять MPP, для нас является открытым. Однако мы ведем активные исследования, чтобы на практике реализовать заложенный в MPP-подходе потенциал.
Одна из проблем мониторинга моделей — существенный временной разрыв между датой прогноза и наблюдением фактического значения целевой переменной. Под катом мы расскажем про новые методы, которые прогнозируют снижение предсказательной способности модели.

Моделирование в банке не разовое упражнение, а сложный процесс. Важно как можно раньше идентифицировать снижение качества модели, особенно во времена резко меняющихся экономических условий.
Для «вызревания» многих целевых переменных в прикладных банковских задачах требуются существенные временные периоды. Например, в задачах кредитного скоринга временной горизонт прогнозирования события дефолта составляет 12 месяцев. То есть оценить качество работы, сравнив прогнозные значения вероятностей дефолта с фактически реализовавшимися дефолтами, мы можем только по состоянию на год назад.
«Классические» подходы к снижению модельных рисков базируются на такой гипотезе: существенные отклонения в распределении входных факторов модели могут сигнализировать о нерепрезентативности разработанной модели для текущего входного потока. Чтобы контролировать стабильность факторов модели, в большинстве случаев используют следующие статистические метрики:
- Population stability index (PSI).
- Тест Колмогорова-Смирнова (KS).
У «классических» подходов есть существенные недостатки. Главный из них — контроль стабильности маржинальных (одномерных) распределений факторов, а не совместного (многомерного) распределения, на котором фактически базируется модель. Например, в модели кредитного скоринга могут использоваться факторы возраста и дохода. Если смотреть на факторы по отдельности, возрастная структура и структура доходов входного потока могут почти не меняться. При этом доход может перераспределиться от более возрастных клиентов к более молодым. В результате «классический» подход к мониторингу не выявит изменений, а модель будет в основном применяться на тех участках распределения входного потока, для которых было относительно мало наблюдений в выборке для обучения, следовательно, ошибка прогнозирования может значимо вырасти.
Другими недостатками «классического» подхода является единообразность и неинтуитивность устанавливаемых порогов для мониторинга, а также отсутствие связи устанавливаемых порогов мониторинга и целевой переменной модели.
Подход на основе Model Performance Predictor
В подходе MPP (Model Performance Predictor) мы хотим, чтобы модель следила за моделью. И задача следящей модели — предсказывать, как будет ошибаться первая модель в своем прогнозе.
Возможная схема обучения MPP приведена на рисунке ниже.

Изначально мы делим выборку на test/train. На train выборке мы применяем стандартные ML pipeline без изменений, а вот в части test происходит вся магия: после подсчета метрик качества на test мы разбиваем эту часть еще на две — MPP train и MPP test — и используем для тренировки в качестве целевой метрики метрику ошибки изначальной модели. В таком контексте определение порогов тоже может быть параметром, который мы оцениваем по данным.
То есть первая модель предсказывает результат, а вторая показывает, насколько первая модель ошибается в своем прогнозе.
Заметим, что данный процесс — это не стекинг, как может изначально показаться, потому что выборки разные: MPP модель обучается на test’е.
И еще данный метод «честнее», чем доверительные интервалы: MPP строится на test’е, в то время как доверительный интервал оценивается на исходных тренировочных данных.
Особенно интересен этот подход, если data scientist ограничен трактуемым классом моделей при разработке. MPP-подход полностью развязывает ему руки при контроле данных моделей, а значит, позволяет использовать весь арсенал продвинутых методов для любой задачи.
Как насчет нарушения «No free lunch theorem»? С точки зрения теории машинного обучения, MPP-подход дает преимущества за счет того, что тестовая выборка используется на все 100% и для валидации модели, и для обучения/проверки модели MPP.
Преимущества MPP
Разберем основные плюсы подхода чуть более формально:
- MPP-модель будет «искать» области совместного распределения факторов, в которых первичная модель будет «плохо» либо «хорошо» работать.
- В качестве целевой переменной для MPP-модели может быть установлена любая интуитивная метрика качества работы первичной модели.
- Если мы ограничены линейными или квазилинейными моделями (регуляторные ограничения либо высокие модельные риски), данный подход позволит нам нелинейно «следить» за целевой переменной, не нарушая требований регулятора.
Недостаток в том, что это создает дополнительные сложности и затраты для разработки и внедрения одновременно двух моделей.
MPP: пример работы
В демонстрационных целях построена простая линейная модель прогноза среднего за 10 торговых дней значения индекса МосБиржи MOEX (train: 06.2010-06.2015).
Демонстрационная модель построена на открытых данных, поскольку мы не можем раскрывать реальные данные Банка. Однако, контроль ошибки модели чрезвычайно важен в самых ключевых бизнес-процессах банка, например, в кредитном скоринге, который характеризуется большими временными лагами между наблюдением целевой переменной и прогнозом.
График демонстрирует работу модели на out-of-time выборке, ошибка (error) была использована для обучения модели MPP (период с 01.2020 был использован как out-of-sample для MPP-модели):

На графике видно, как меняется парадигма: с COVID-19 не просто изменяются предсказания, но еще больше изменяются ошибки модели. Это сразу говорит о том, что модель, обученная на предыдущих исторических данных, не отражает текущую ситуацию.
MPP: результаты демонстрационного примера
На данных об ошибке первичной модели была обучена нейронная сеть:
GRUModel(
(cell): GRU(2, 32, num_layers=2, batch_first=True, dropout=0.5)
(relu): ReLU()
(fc_inner): Linear(in_features=32, out_features=32, bias=True)
(fc): Linear(in_features=32, out_features=1, bias=True)
)

Модель не смогла предсказать глубину стресса и направление изменения ошибки, но просигнализировала о смене рыночной конъюнктуры, подняв прогноз ошибки до исторических максимумов.
Более тщательный fine-tuning модели и включение в выборку для обучения периодов исторического стресса потенциально должны улучшить чувствительность MPP-подхода (эти работы не были выполнены, т. к. задача исключительно демонстрационная).
Пробитие порогов в мониторинге может вести к различным управленческим решениям — от долгосрочных (перестроение модели) до моментальных (изменение порогов модельной отсечки при принятии автоматических решений).
Направления для дальнейших исследований и открытые вопросы
Тестовое использование MPP-подхода выявило ряд вопросов:
- «Вручную» строить две модели слишком затратно по времени. Какие AutoML подходы лучше работают для MPP-задач в кредитном скоринге и других банковских задачах?
- Какие метрики ошибок первичных моделей лучше использовать как целевые переменные для MPP-моделей?
- Как работает MPP-мониторинг в периоды экономического стресса?
Вопрос о том, как эффективно применять MPP, для нас является открытым. Однако мы ведем активные исследования, чтобы на практике реализовать заложенный в MPP-подходе потенциал.
