Рассказывая о вероятностном программировании и Байесовской статистике, я обычно не уделяю особого внимания тому, как, на самом деле, выполняется вероятностный вывод, рассматривая его как некий «чёрный ящик». Вся прелесть вероятностного программирования заключается в том, что, на самом деле, для того, чтобы строить модели, не обязательно понимать, как именно делается вывод. Но это знание, безусловно, весьма полезно.

Как-то раз я рассказывал о новой Байесовской модели человеку, который не особенно разбирался в предмете, но очень хотел всё понять. Он-то и спросил меня о том, чего я обычно не касаюсь. «Томас, — сказал он, — а как, на самом деле, выполняется вероятностный вывод? Как получаются эти таинственные сэмплы из апостериорной вероятности?».
Тут я мог бы сказать: «Всё очень просто. MCMC генерирует сэмплы из апостериорного распределения вероятностей, создавая обратимую цепь Маркова, равновесное распределение которой – это целевое апостериорное распределение. Вопросы?».
Объяснение это верное, но много ли от него пользы для непосвящённого? Меня больше всего раздражает в том, как учат математике и статистике, то, что никто никогда не говорит об интуитивно понятных идеях, лежащих в основе всяческих понятий. А эти идеи обычно довольно просты. С таких занятий можно вынести трёхэтажные математические формулы, но не понимание того, как всё устроено. Меня учили именно так, а я хотел понять. Я бессчётные часы бился головой о математические стены, прежде чем наступал момент очередного прозрения, прежде чем очередная «Эврика!» срывалась с моих губ. После того, как мне удавалось разобраться, то, что раньше виделось сложным, оказывалось на удивление простым. То, что раньше пугало нагромождением математических знаков, становилось полезным инструментом.
Этот материал – попытка интуитивно понятного объяснения MCMC-сэмплинга (в частности, алгоритма Метрополиса). Мы будем использовать примеры кода вместо формул или математических выкладок. В конечном итоге, без формул не обойтись, но лично я считаю, что лучше всего начинать с примеров и достичь интуитивного понимания вопроса, прежде чем переходить к языку математики.
Взглянем на формулу Байеса:
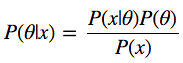
У нас есть P(θ|x) – то, что нас интересует, а именно – апостериорная вероятность, или распределение вероятностей параметров модели θ, вычисленная после того, как приняты во внимание данные x, взятые из наблюдений. Для того, чтобы получить то, что нам нужно, надо перемножить априорную вероятность P(θ), то есть – то, что мы думаем о θ до проведения экспериментов, до получения данных, и функцию правдоподобия P(x|θ), то есть – то, что мы думаем о том, как распределены данные. Числитель дроби найти очень легко.
Теперь присмотримся к знаменателю P(x), который ещё называют свидетельством, то есть – свидетельством того, что данные х, были сгенерированы этой моделью. Вычислить его можно, проинтегрировав все возможные значения параметров:
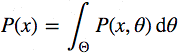
Вот в этом – основная сложность формулы Байеса. Сама она выглядит вполне невинно, но даже для слегка нетривиальной модели апостериорную вероятность не вычислить за конечное число шагов.
Тут можно сказать: «Хорошо, если напрямую это не решается, можем ли мы пойти по пути аппроксимации? Например, если бы мы могли бы как-нибудь получить образцы данных из этой самой апостериорной вероятности, их можно было бы аппроксимировать методом Монте-Карло.» К несчастью, для того, чтобы взять сэмплы из распределения, надо не только найти решение формулы Байеса, но ещё и инвертировать её, поэтому такой подход даже сложнее.
Продолжая размышления, можно заявить: «Ладно, тогда давайте сконструируем цепь Маркова, равновесное распределение которой совпадает с нашим апостериорным распределением». Я, конечно, шучу. Большинство людей так не выразится, очень уж безумно это звучит. Если вычислить напрямую нельзя, взять сэмплы из распределения тоже нельзя, то построить цепь Маркова с вышеозначенными свойствами – задача и вовсе неподъёмная.
И вот здесь нас ждёт удивительное открытие. Сделать это, на самом деле, очень легко. Существует целый класс алгоритмов для решения таких задач: методы Монте-Карло в Марковских цепях (Markov Chain Monte Carlo, MCMC). Сущность этих алгоритмов – создание цепи Маркова для выполнения аппроксимации методом Монте-Карло.
Для начала импортируем необходимые модули. Блоки кода, отмеченные как «Листинг», можно вставить в Jupyter Notebook и, по мере чтения материала, опробовать в деле. Полный исходник смотрите здесь.
Теперь сгенерируем данные. Это будут 100 точек, нормально распределённых вокруг нуля. Наша цель заключается в том, чтобы оценить апостериорное распределение средней mu (предполагается, что мы знаем, что среднеквадратическое отклонение равно 1).
Теперь построим гистограмму.
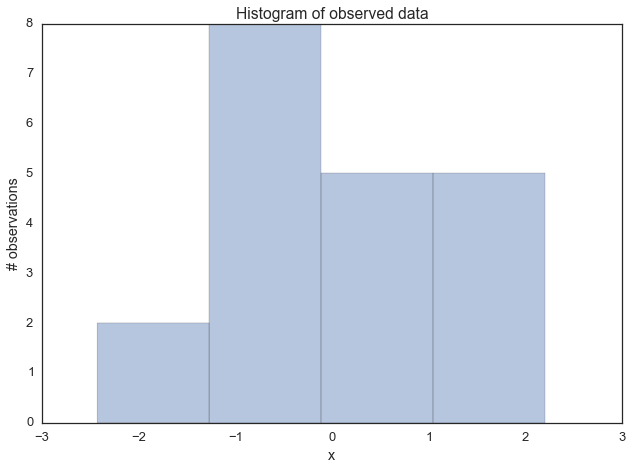
Гистограмма наблюдаемых данных
Теперь нужно описать модель. Мы рассматриваем простой случай, поэтому предполагаем, что данные распределены нормально, то есть, функция правдоподобия модели так же распределена нормально. Как вы, должно быть, знаете, у нормального распределения есть два параметра – это математическое ожидание (среднее значение) μ и среднеквадратическое отклонение σ. Для простоты, будем считать, что мы знаем, что σ=1. Мы хотим вывести апостериорную вероятность для μ. Для каждого искомого параметра нужно выбрать априорное распределение вероятностей. Для простоты, допустим, что нормальное распределение будет априорным распределением для μ. Таким образом, на языке статистики, модель будет выглядеть так:
Что особенно удобно – для этой модели, на самом деле, можно вычислить апостериорное распределение вероятностей аналитически. Дело в том, что для нормальной функции правдоподобия с известным среднеквадратическим отклонением, нормальное априорное распределение вероятностей для mu является сопряжённым априорным распределением. То есть, наше апостериорное распределение будет следовать тому же распределению, что и априорное. В итоге, мы знаем, что апостериорное распределение для μ так же является нормальным. В Википедии несложно найти методику расчёта параметров для апостериорного распределения. Математическое описание этого можно найти здесь.
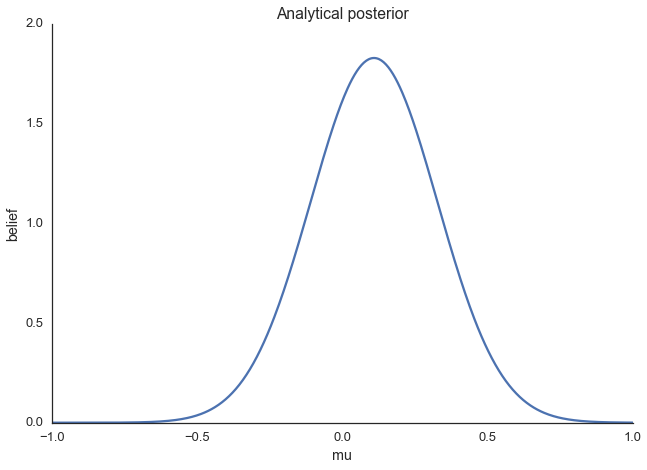
Апостериорное распределение, найденное аналитически
Здесь изображено то, что нас интересует, то есть, распределение вероятностей для значений μ после учёта имеющихся данных, принимая во внимание априорную информацию. Предположим, однако, что априорное распределение не является сопряжённым и мы не можем решить задачу, так сказать, вручную. На практике обычно бывает именно так.
Теперь поговорим о сэмплировании. Во-первых, нужно найти начальную позицию параметра (её можно выбрать случайным образом). Давайте зададим её произвольно следующим образом:
Затем предлагается переместиться, «прыгнуть» из этой позиции в какое-то другое место (это уже относится к цепям Маркова). Эту новую позицию можно выбрать и «методом тыка», и руководствуясь какими-то глубокими соображениями. Сэмплер в алгоритме Метрополиса прост, как пять копеек: он выбирает образец из нормального распределения с центром в текущем значении mu (переменная mu_current) с неким среднеквадратическим отклонением (proposal_width), которое определяет ширину диапазона, из которого выбираются предлагаемые значения. Здесь мы используем scipy.stats.norm. Надо сказать, что вышеупомянутое нормальное распределение не имеет ничего общего с тем, что используется в модели.
Следующий шаг – оценка того, подходящее ли место выбрано для перехода. Если полученное нормальное распределение с предложенным mu объясняет данные лучше, чем при предыдущем mu, то в выбранном направлении, безусловно, стоит двигаться. Но что значит «лучше объясняет данные»? Мы определяем это понятие, вычисляя вероятность данных, учитывая функцию правдоподобия (нормальную) с предложенными значениями параметров (предложенное mu и sigma, значение которого зафиксировано и равно 1). Расчёты тут простые. Достаточно вычислить вероятность для каждой точки данных с помощью команды scipy.stats.normal(mu, sigma).pdf(data) и затем перемножить индивидуальные вероятности, то есть – найти значение функции правдоподобия. Обычно в таком случае пользуются логарифмическим распределением вероятностей, но здесь мы это опускаем.
До этого момента мы, на самом деле, пользовались алгоритмом восхождения к вершине, который лишь предлагает перемещения в случайных направлениях и принимает новое положение только если mu_proposal имеет более высокий уровень правдоподобия, нежели mu_current. В конечном итоге мы дойдём до варианта mu = 0 (или к значению, близкому к этому), откуда двигаться будет уже некуда. Однако, мы хотим получить апостериорное распределение, поэтому должны иногда соглашаться на перемещения в другом направлении. Главный секрет здесь заключается в том, что разделив p_proposal на p_current, мы получим вероятность принятия предложения.
Можно заметить, что если p_proposal больше, чем p_current, полученная вероятность будет больше 1, и такое предложение мы, определённо, примем. Однако, если p_current больше чем p_proposal, скажем, в два раза, шанс перехода будет составлять уже 50%:
Эта простая процедура даёт нам сэмплы из апостериорного распределения.
Оглянемся назад и отметим, что введение в систему вероятности принятия предлагаемой позиции перехода – это причина, по которой всё это работает и позволяет нам избежать интегрирования. Это хорошо видно, если вычислять уровень принятия предложения для нормализованного апостериорного распределения и наблюдать за тем, как он соотносится с уровнем принятия предложения для ненормализованного апостериорного распределения (скажем, μ0 – это текущая позиция, а μ это предлагаемая новая позиция):
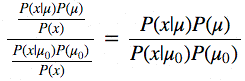
Если это объяснить, то, деля ту апостериорную вероятность, которая получилась для предлагаемого параметра, на ту, что вычислена для текущего параметра, мы избавляемся от уже надоевшего P(x), которое посчитать не в состоянии. Можно интуитивно понять, что мы делим полное апостериорное распределение вероятностей в одной позиции на то же самое в другой позиции (вполне обычная операция). Таким образом мы посещаем области с более высоким уровнем апостериорного распределения вероятностей сравнительно более часто, чем области с низким уровнем.
Соберём вышесказанное воедино.
Для того, чтобы визуализировать процесс сэмплирования, мы рисуем графики некоторых вычисляемых величин. Каждый ряд изображений представляет собой один проход Метрополис-сэмплера.
В первом столбце показано априорное распределение вероятностей, то есть – наши предположения о μ до ознакомления с данными. Как можно видеть, это распределение не меняется, мы лишь показываем здесь предложения нового значения μ. Вертикальные синие линии – это текущее μ. А предлагаемое μ отображается либо зелёным, либо красным цветом (это, соответственно, принятые и отвергнутые предложения).
Во втором столбце – функция правдоподобия и то, что мы используем для того, чтобы оценить, насколько хорошо модель объясняет данные. Здесь можно заметить, что график меняется в соответствии с предлагаемым μ. Там же отображается и синяя гистограмма – сами данные. Сплошная линия выводится либо зелёным, либо красным цветом – это график функции правдоподобия при mu, предложенном на текущем шаге. Чисто интуитивно понятно, что чем сильнее функция правдоподобия перекрывается с графическим отображением данных – тем лучше модель объясняет данные и тем выше будет результирующая вероятность. Точечная линия того же цвета – это предложенное mu, точечная синяя линия – это текущее mu.
В третьей колонке – апостериорное распределение вероятностей. Здесь показано нормализованное апостериорное распределение, но, как мы выяснили выше, можно просто умножить предыдущее значение для текущего и предложенного μ на значение функции правдоподобия для двух μ для того, чтобы получить ненормализованные значения апостериорного распределения (что мы и используем для реальных вычислений), и разделить одно на другое для того, чтобы получить вероятность принятия предложенного значения.
В четвёртой колонке представлен след выборки, то есть – значения μ, сэмплы, полученные на основе модели. Здесь мы показываем каждый сэмпл, вне зависимости от того, был ли он принят или отвергнут (в таком случае линия не меняется).
Обратите внимание на то, что мы всегда двигаемся к сравнительно более правдоподобным значениям μ (в плане плотности их апостериорного распределения вероятности) и лишь иногда – к сравнительно менее правдоподобным значениям μ. Например, как в итерации №1 (номера итераций можно видеть в верхней части каждого ряда изображений по центру.







Визуализация MCMC
Замечательное свойство MCMC заключается в том, что для получения нужного результата вышеописанный процесс просто нужно достаточно долго повторять. Сэмплы, генерируемые таким образом, берутся из апостериорного распределения вероятностей исследуемой модели. Есть строгое математическое доказательство, которое гарантирует, что это именно так и будет, но здесь я не хочу вдаваться в такие подробности.
Для того, чтобы получить представление о том, какие именно данные производит система, давайте сгенерируем большое количество сэмплов и представим их графически.
Визуализация 15000 сэмплов
Это обычно называют следом выборки. Теперь, для того, чтобы получить приближённое значение апостериорного распределения вероятностей (собственно говоря, это нам и нужно), достаточно построить гистограмму этих данных. Важно помнить, что, хотя полученные данные похожи на те, сэмплированием которых мы занимались для подгонки модели, это два разных набора данных.
Нижеприведённый график отражает наше представление о том, каким должно быть mu. В данном случае так получилось, что он тоже демонстрирует нормальное распределение, но для другой модели он мог бы иметь совершенно иную форму, нежели график функции правдоподобия или априорного распределения вероятностей.

Аналитическое и оценочное апостериорные распределения вероятностей
Как можно заметить, следуя вышеописанному методу, мы получили сэмплы из того же распределения вероятностей, что было получено аналитическим путём.
Выше мы задали интервал, из которого выбираются предлагаемые значения, равным 0,5. Именно это значение оказалось очень удачным. В общем случае, ширина диапазона не должна быть слишком маленькой, иначе сэмплинг будет неэффективным, так как для исследования пространства параметров понадобится слишком много времени и модель будет демонстрировать типичное для случайного блуждания поведение.
Вот, например, что мы получили, установив параметр proposal_width в значение 0,01.

Результат использования слишком маленького диапазона
Слишком большой интервал тоже не подойдёт – предлагаемые для перехода значения будут постоянно отвергаться. Вот, что будет, если установить proposal_width в значение 3.
Результат использования слишком большого диапазона
Однако, обратите внимание на то, что мы здесь продолжаем брать сэмплы из целевого апостериорного распределения, как гарантирует математическое доказательство. Но такой подход менее эффективен.
Маленький и большой размер шага
С использованием большого количества итераций, то, что у нас получится, в конечном счёте, будет выглядеть как настоящее апостериорное распределение. Главное то, что нам нужно, чтобы сэмплы были независимы друг от друга. В данном случае это, очевидно, не так. Для того, чтобы оценить эффективность нашего сэмплера, можно воспользоваться показателем автокорреляции. То есть – узнать, как образец i коррелирует с образцом i-1, i-2, и так далее.

Автокорреляция для маленького, среднего и большого размера шага
Очевидно то, что хотелось бы иметь интеллектуальный способ автоматического определения подходящего размера шага. Один из обычно используемых методов заключается в такой подстройке интервала, из которого выбирают значения, чтобы примерно 50% предложений отбрасывалось. Что интересно, другие алгоритмы MCMC, вроде Гибридного метода Монте-Карло (Hamiltonian Monte Carlo) очень похожи на тот, о котором мы говорили. Главная их особенность заключается в том, что они ведут себя «умнее», когда выдвигают предложения для следующего «прыжка».
Теперь легко представить, что мы могли бы добавить параметр sigma для среднеквадратического отклонения и следовать той же процедуре для второго параметра. В таком случае генерировались бы предложения для mu и sigma, но логика алгоритма практически не изменилась бы. Или мы могли бы брать данные из очень разных распределений вероятностей, вроде биномиального, и, продолжая пользоваться тем же алгоритмом, получали бы правильное апостериорное распределение вероятностей. Это просто здорово, это – одно из огромных преимуществ вероятностного программирования: достаточно определить желаемую модель и позволить MCMC заниматься байесовским выводом.
Вот, например, нижеприведённую модель можно очень легко описать средствами PyMC3. Так же, в этом примере мы пользуемся Метрополис-сэмплером (с автоматически настраиваемой шириной диапазона, из которого берутся предлагаемые значения) и видим, что результаты практически идентичны. Можете с этим поэкспериментировать, поменять распределение, например. В документации по PyMC3 можно найти более сложные примеры и сведения о том, как всё это работает.
Результаты работы различных сэмплеров
Надеемся, мы смогли донести до вас сущность MCMC, Метрополис-сэмплера, вероятностного вывода, и теперь у вас появилось интуитивное понимание всего этого. А значит – вы готовы к чтению материалов по данному вопросу, насыщенных математическими формулами. Там вы сможете найти все те детали, которые мы обошли здесь стороной для того, чтобы не скрыть за ними самого главного.

Как-то раз я рассказывал о новой Байесовской модели человеку, который не особенно разбирался в предмете, но очень хотел всё понять. Он-то и спросил меня о том, чего я обычно не касаюсь. «Томас, — сказал он, — а как, на самом деле, выполняется вероятностный вывод? Как получаются эти таинственные сэмплы из апостериорной вероятности?».
Тут я мог бы сказать: «Всё очень просто. MCMC генерирует сэмплы из апостериорного распределения вероятностей, создавая обратимую цепь Маркова, равновесное распределение которой – это целевое апостериорное распределение. Вопросы?».
Объяснение это верное, но много ли от него пользы для непосвящённого? Меня больше всего раздражает в том, как учат математике и статистике, то, что никто никогда не говорит об интуитивно понятных идеях, лежащих в основе всяческих понятий. А эти идеи обычно довольно просты. С таких занятий можно вынести трёхэтажные математические формулы, но не понимание того, как всё устроено. Меня учили именно так, а я хотел понять. Я бессчётные часы бился головой о математические стены, прежде чем наступал момент очередного прозрения, прежде чем очередная «Эврика!» срывалась с моих губ. После того, как мне удавалось разобраться, то, что раньше виделось сложным, оказывалось на удивление простым. То, что раньше пугало нагромождением математических знаков, становилось полезным инструментом.
Этот материал – попытка интуитивно понятного объяснения MCMC-сэмплинга (в частности, алгоритма Метрополиса). Мы будем использовать примеры кода вместо формул или математических выкладок. В конечном итоге, без формул не обойтись, но лично я считаю, что лучше всего начинать с примеров и достичь интуитивного понимания вопроса, прежде чем переходить к языку математики.
Проблема и её неинтуитивное решение
Взглянем на формулу Байеса:
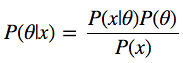
У нас есть P(θ|x) – то, что нас интересует, а именно – апостериорная вероятность, или распределение вероятностей параметров модели θ, вычисленная после того, как приняты во внимание данные x, взятые из наблюдений. Для того, чтобы получить то, что нам нужно, надо перемножить априорную вероятность P(θ), то есть – то, что мы думаем о θ до проведения экспериментов, до получения данных, и функцию правдоподобия P(x|θ), то есть – то, что мы думаем о том, как распределены данные. Числитель дроби найти очень легко.
Теперь присмотримся к знаменателю P(x), который ещё называют свидетельством, то есть – свидетельством того, что данные х, были сгенерированы этой моделью. Вычислить его можно, проинтегрировав все возможные значения параметров:
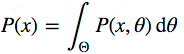
Вот в этом – основная сложность формулы Байеса. Сама она выглядит вполне невинно, но даже для слегка нетривиальной модели апостериорную вероятность не вычислить за конечное число шагов.
Тут можно сказать: «Хорошо, если напрямую это не решается, можем ли мы пойти по пути аппроксимации? Например, если бы мы могли бы как-нибудь получить образцы данных из этой самой апостериорной вероятности, их можно было бы аппроксимировать методом Монте-Карло.» К несчастью, для того, чтобы взять сэмплы из распределения, надо не только найти решение формулы Байеса, но ещё и инвертировать её, поэтому такой подход даже сложнее.
Продолжая размышления, можно заявить: «Ладно, тогда давайте сконструируем цепь Маркова, равновесное распределение которой совпадает с нашим апостериорным распределением». Я, конечно, шучу. Большинство людей так не выразится, очень уж безумно это звучит. Если вычислить напрямую нельзя, взять сэмплы из распределения тоже нельзя, то построить цепь Маркова с вышеозначенными свойствами – задача и вовсе неподъёмная.
И вот здесь нас ждёт удивительное открытие. Сделать это, на самом деле, очень легко. Существует целый класс алгоритмов для решения таких задач: методы Монте-Карло в Марковских цепях (Markov Chain Monte Carlo, MCMC). Сущность этих алгоритмов – создание цепи Маркова для выполнения аппроксимации методом Монте-Карло.
Постановка задачи
Для начала импортируем необходимые модули. Блоки кода, отмеченные как «Листинг», можно вставить в Jupyter Notebook и, по мере чтения материала, опробовать в деле. Полный исходник смотрите здесь.
▍Листинг 1
%matplotlib inline
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
sns.set_style('white')
sns.set_context('talk')
np.random.seed(123)Теперь сгенерируем данные. Это будут 100 точек, нормально распределённых вокруг нуля. Наша цель заключается в том, чтобы оценить апостериорное распределение средней mu (предполагается, что мы знаем, что среднеквадратическое отклонение равно 1).
▍Листинг 2
data = np.random.randn(20)Теперь построим гистограмму.
▍Листинг 3
ax = plt.subplot()
sns.distplot(data, kde=False, ax=ax)
_ = ax.set(title='Histogram of observed data', xlabel='x', ylabel='# observations');
Гистограмма наблюдаемых данных
Теперь нужно описать модель. Мы рассматриваем простой случай, поэтому предполагаем, что данные распределены нормально, то есть, функция правдоподобия модели так же распределена нормально. Как вы, должно быть, знаете, у нормального распределения есть два параметра – это математическое ожидание (среднее значение) μ и среднеквадратическое отклонение σ. Для простоты, будем считать, что мы знаем, что σ=1. Мы хотим вывести апостериорную вероятность для μ. Для каждого искомого параметра нужно выбрать априорное распределение вероятностей. Для простоты, допустим, что нормальное распределение будет априорным распределением для μ. Таким образом, на языке статистики, модель будет выглядеть так:
μ∼Normal(0,1)
x|μ∼Normal(x;μ,1)Что особенно удобно – для этой модели, на самом деле, можно вычислить апостериорное распределение вероятностей аналитически. Дело в том, что для нормальной функции правдоподобия с известным среднеквадратическим отклонением, нормальное априорное распределение вероятностей для mu является сопряжённым априорным распределением. То есть, наше апостериорное распределение будет следовать тому же распределению, что и априорное. В итоге, мы знаем, что апостериорное распределение для μ так же является нормальным. В Википедии несложно найти методику расчёта параметров для апостериорного распределения. Математическое описание этого можно найти здесь.
▍Листинг 4
def calc_posterior_analytical(data, x, mu_0, sigma_0):
sigma = 1.
n = len(data)
mu_post = (mu_0 / sigma_0**2 + data.sum() / sigma**2) / (1. / sigma_0**2 + n / sigma**2)
sigma_post = (1. / sigma_0**2 + n / sigma**2)**-1
return norm(mu_post, np.sqrt(sigma_post)).pdf(x)
ax = plt.subplot()
x = np.linspace(-1, 1, 500)
posterior_analytical = calc_posterior_analytical(data, x, 0., 1.)
ax.plot(x, posterior_analytical)
ax.set(xlabel='mu', ylabel='belief', title='Analytical posterior');
sns.despine()
Апостериорное распределение, найденное аналитически
Здесь изображено то, что нас интересует, то есть, распределение вероятностей для значений μ после учёта имеющихся данных, принимая во внимание априорную информацию. Предположим, однако, что априорное распределение не является сопряжённым и мы не можем решить задачу, так сказать, вручную. На практике обычно бывает именно так.
Код, как путь к пониманию сущности MCMC-сэмплинга
Теперь поговорим о сэмплировании. Во-первых, нужно найти начальную позицию параметра (её можно выбрать случайным образом). Давайте зададим её произвольно следующим образом:
mu_current = 1.Затем предлагается переместиться, «прыгнуть» из этой позиции в какое-то другое место (это уже относится к цепям Маркова). Эту новую позицию можно выбрать и «методом тыка», и руководствуясь какими-то глубокими соображениями. Сэмплер в алгоритме Метрополиса прост, как пять копеек: он выбирает образец из нормального распределения с центром в текущем значении mu (переменная mu_current) с неким среднеквадратическим отклонением (proposal_width), которое определяет ширину диапазона, из которого выбираются предлагаемые значения. Здесь мы используем scipy.stats.norm. Надо сказать, что вышеупомянутое нормальное распределение не имеет ничего общего с тем, что используется в модели.
proposal = norm(mu_current, proposal_width).rvs()Следующий шаг – оценка того, подходящее ли место выбрано для перехода. Если полученное нормальное распределение с предложенным mu объясняет данные лучше, чем при предыдущем mu, то в выбранном направлении, безусловно, стоит двигаться. Но что значит «лучше объясняет данные»? Мы определяем это понятие, вычисляя вероятность данных, учитывая функцию правдоподобия (нормальную) с предложенными значениями параметров (предложенное mu и sigma, значение которого зафиксировано и равно 1). Расчёты тут простые. Достаточно вычислить вероятность для каждой точки данных с помощью команды scipy.stats.normal(mu, sigma).pdf(data) и затем перемножить индивидуальные вероятности, то есть – найти значение функции правдоподобия. Обычно в таком случае пользуются логарифмическим распределением вероятностей, но здесь мы это опускаем.
likelihood_current = norm(mu_current, 1).pdf(data).prod()
likelihood_proposal = norm(mu_proposal, 1).pdf(data).prod()
# Вычисление априорного распределения вероятности для текущего и предложенного mu
prior_current = norm(mu_prior_mu, mu_prior_sd).pdf(mu_current)
prior_proposal = norm(mu_prior_mu, mu_prior_sd).pdf(mu_proposal)
# Числитель формулы Байеса
p_current = likelihood_current * prior_current
p_proposal = likelihood_proposal * prior_proposalДо этого момента мы, на самом деле, пользовались алгоритмом восхождения к вершине, который лишь предлагает перемещения в случайных направлениях и принимает новое положение только если mu_proposal имеет более высокий уровень правдоподобия, нежели mu_current. В конечном итоге мы дойдём до варианта mu = 0 (или к значению, близкому к этому), откуда двигаться будет уже некуда. Однако, мы хотим получить апостериорное распределение, поэтому должны иногда соглашаться на перемещения в другом направлении. Главный секрет здесь заключается в том, что разделив p_proposal на p_current, мы получим вероятность принятия предложения.
p_accept = p_proposal / p_currentМожно заметить, что если p_proposal больше, чем p_current, полученная вероятность будет больше 1, и такое предложение мы, определённо, примем. Однако, если p_current больше чем p_proposal, скажем, в два раза, шанс перехода будет составлять уже 50%:
accept = np.random.rand() < p_accept
if accept:
# Обновляем позицию
cur_pos = proposalЭта простая процедура даёт нам сэмплы из апостериорного распределения.
Зачем это всё?
Оглянемся назад и отметим, что введение в систему вероятности принятия предлагаемой позиции перехода – это причина, по которой всё это работает и позволяет нам избежать интегрирования. Это хорошо видно, если вычислять уровень принятия предложения для нормализованного апостериорного распределения и наблюдать за тем, как он соотносится с уровнем принятия предложения для ненормализованного апостериорного распределения (скажем, μ0 – это текущая позиция, а μ это предлагаемая новая позиция):

Если это объяснить, то, деля ту апостериорную вероятность, которая получилась для предлагаемого параметра, на ту, что вычислена для текущего параметра, мы избавляемся от уже надоевшего P(x), которое посчитать не в состоянии. Можно интуитивно понять, что мы делим полное апостериорное распределение вероятностей в одной позиции на то же самое в другой позиции (вполне обычная операция). Таким образом мы посещаем области с более высоким уровнем апостериорного распределения вероятностей сравнительно более часто, чем области с низким уровнем.
Складываем полную картину
Соберём вышесказанное воедино.
▍Листинг 5
def sampler(data, samples=4, mu_init=.5, proposal_width=.5, plot=False, mu_prior_mu=0, mu_prior_sd=1.):
mu_current = mu_init
posterior = [mu_current]
for i in range(samples):
# предлагаем новую позицию
mu_proposal = norm(mu_current, proposal_width).rvs()
# Вычисляем правдоподобие, перемножая вероятности для каждой точки данных
likelihood_current = norm(mu_current, 1).pdf(data).prod()
likelihood_proposal = norm(mu_proposal, 1).pdf(data).prod()
# Вычисляем априорное распределение вероятностей для текущего и предлагаемого mu
prior_current = norm(mu_prior_mu, mu_prior_sd).pdf(mu_current)
prior_proposal = norm(mu_prior_mu, mu_prior_sd).pdf(mu_proposal)
p_current = likelihood_current * prior_current
p_proposal = likelihood_proposal * prior_proposal
# Принять предложенную точку?
p_accept = p_proposal / p_current
# Обычно сюда было бы включено априорное распределение вероятностей, здесь это опущено для простоты
accept = np.random.rand() < p_accept
if plot:
plot_proposal(mu_current, mu_proposal, mu_prior_mu, mu_prior_sd, data, accept, posterior, i)
if accept:
# Обновляем позицию
mu_current = mu_proposal
posterior.append(mu_current)
return posterior
# Функция визуализации
def plot_proposal(mu_current, mu_proposal, mu_prior_mu, mu_prior_sd, data, accepted, trace, i):
from copy import copy
trace = copy(trace)
fig, (ax1, ax2, ax3, ax4) = plt.subplots(ncols=4, figsize=(16, 4))
fig.suptitle('Iteration %i' % (i + 1))
x = np.linspace(-3, 3, 5000)
color = 'g' if accepted else 'r'
# Визуализация априорного распределения вероятностей
prior_current = norm(mu_prior_mu, mu_prior_sd).pdf(mu_current)
prior_proposal = norm(mu_prior_mu, mu_prior_sd).pdf(mu_proposal)
prior = norm(mu_prior_mu, mu_prior_sd).pdf(x)
ax1.plot(x, prior)
ax1.plot([mu_current] * 2, [0, prior_current], marker='o', color='b')
ax1.plot([mu_proposal] * 2, [0, prior_proposal], marker='o', color=color)
ax1.annotate("", xy=(mu_proposal, 0.2), xytext=(mu_current, 0.2),
arrowprops=dict(arrowstyle="->", lw=2.))
ax1.set(ylabel='Probability Density', title='current: prior(mu=%.2f) = %.2f\nproposal: prior(mu=%.2f) = %.2f' % (mu_current, prior_current, mu_proposal, prior_proposal))
# Правдоподобие
likelihood_current = norm(mu_current, 1).pdf(data).prod()
likelihood_proposal = norm(mu_proposal, 1).pdf(data).prod()
y = norm(loc=mu_proposal, scale=1).pdf(x)
sns.distplot(data, kde=False, norm_hist=True, ax=ax2)
ax2.plot(x, y, color=color)
ax2.axvline(mu_current, color='b', linestyle='--', label='mu_current')
ax2.axvline(mu_proposal, color=color, linestyle='--', label='mu_proposal')
#ax2.title('Proposal {}'.format('accepted' if accepted else 'rejected'))
ax2.annotate("", xy=(mu_proposal, 0.2), xytext=(mu_current, 0.2),
arrowprops=dict(arrowstyle="->", lw=2.))
ax2.set(title='likelihood(mu=%.2f) = %.2f\nlikelihood(mu=%.2f) = %.2f' % (mu_current, 1e14*likelihood_current, mu_proposal, 1e14*likelihood_proposal))
# Апостериорное распределение вероятностей
posterior_analytical = calc_posterior_analytical(data, x, mu_prior_mu, mu_prior_sd)
ax3.plot(x, posterior_analytical)
posterior_current = calc_posterior_analytical(data, mu_current, mu_prior_mu, mu_prior_sd)
posterior_proposal = calc_posterior_analytical(data, mu_proposal, mu_prior_mu, mu_prior_sd)
ax3.plot([mu_current] * 2, [0, posterior_current], marker='o', color='b')
ax3.plot([mu_proposal] * 2, [0, posterior_proposal], marker='o', color=color)
ax3.annotate("", xy=(mu_proposal, 0.2), xytext=(mu_current, 0.2),
arrowprops=dict(arrowstyle="->", lw=2.))
#x3.set(title=r'prior x likelihood $\propto$ posterior')
ax3.set(title='posterior(mu=%.2f) = %.5f\nposterior(mu=%.2f) = %.5f' % (mu_current, posterior_current, mu_proposal, posterior_proposal))
if accepted:
trace.append(mu_proposal)
else:
trace.append(mu_current)
ax4.plot(trace)
ax4.set(xlabel='iteration', ylabel='mu', title='trace')
plt.tight_layout()
#plt.legend()Визуализация MCMC
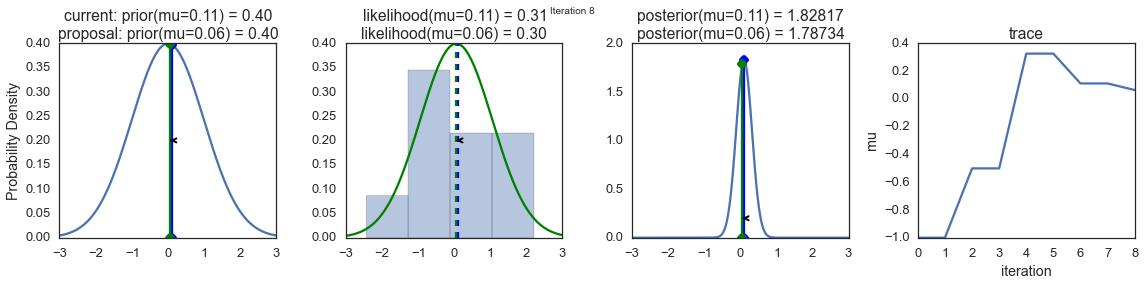
Для того, чтобы визуализировать процесс сэмплирования, мы рисуем графики некоторых вычисляемых величин. Каждый ряд изображений представляет собой один проход Метрополис-сэмплера.
В первом столбце показано априорное распределение вероятностей, то есть – наши предположения о μ до ознакомления с данными. Как можно видеть, это распределение не меняется, мы лишь показываем здесь предложения нового значения μ. Вертикальные синие линии – это текущее μ. А предлагаемое μ отображается либо зелёным, либо красным цветом (это, соответственно, принятые и отвергнутые предложения).
Во втором столбце – функция правдоподобия и то, что мы используем для того, чтобы оценить, насколько хорошо модель объясняет данные. Здесь можно заметить, что график меняется в соответствии с предлагаемым μ. Там же отображается и синяя гистограмма – сами данные. Сплошная линия выводится либо зелёным, либо красным цветом – это график функции правдоподобия при mu, предложенном на текущем шаге. Чисто интуитивно понятно, что чем сильнее функция правдоподобия перекрывается с графическим отображением данных – тем лучше модель объясняет данные и тем выше будет результирующая вероятность. Точечная линия того же цвета – это предложенное mu, точечная синяя линия – это текущее mu.
В третьей колонке – апостериорное распределение вероятностей. Здесь показано нормализованное апостериорное распределение, но, как мы выяснили выше, можно просто умножить предыдущее значение для текущего и предложенного μ на значение функции правдоподобия для двух μ для того, чтобы получить ненормализованные значения апостериорного распределения (что мы и используем для реальных вычислений), и разделить одно на другое для того, чтобы получить вероятность принятия предложенного значения.
В четвёртой колонке представлен след выборки, то есть – значения μ, сэмплы, полученные на основе модели. Здесь мы показываем каждый сэмпл, вне зависимости от того, был ли он принят или отвергнут (в таком случае линия не меняется).
Обратите внимание на то, что мы всегда двигаемся к сравнительно более правдоподобным значениям μ (в плане плотности их апостериорного распределения вероятности) и лишь иногда – к сравнительно менее правдоподобным значениям μ. Например, как в итерации №1 (номера итераций можно видеть в верхней части каждого ряда изображений по центру.
▍Листинг 6
np.random.seed(123)
sampler(data, samples=8, mu_init=-1., plot=True);Визуализация MCMC
Замечательное свойство MCMC заключается в том, что для получения нужного результата вышеописанный процесс просто нужно достаточно долго повторять. Сэмплы, генерируемые таким образом, берутся из апостериорного распределения вероятностей исследуемой модели. Есть строгое математическое доказательство, которое гарантирует, что это именно так и будет, но здесь я не хочу вдаваться в такие подробности.
Для того, чтобы получить представление о том, какие именно данные производит система, давайте сгенерируем большое количество сэмплов и представим их графически.
▍Листинг 7
posterior = sampler(data, samples=15000, mu_init=1.)
fig, ax = plt.subplots()
ax.plot(posterior)
_ = ax.set(xlabel='sample', ylabel='mu');
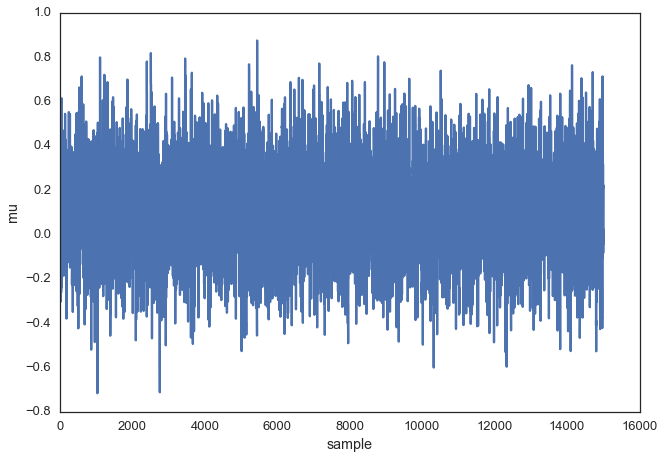
Визуализация 15000 сэмплов
Это обычно называют следом выборки. Теперь, для того, чтобы получить приближённое значение апостериорного распределения вероятностей (собственно говоря, это нам и нужно), достаточно построить гистограмму этих данных. Важно помнить, что, хотя полученные данные похожи на те, сэмплированием которых мы занимались для подгонки модели, это два разных набора данных.
Нижеприведённый график отражает наше представление о том, каким должно быть mu. В данном случае так получилось, что он тоже демонстрирует нормальное распределение, но для другой модели он мог бы иметь совершенно иную форму, нежели график функции правдоподобия или априорного распределения вероятностей.
▍Листинг 8
ax = plt.subplot()
sns.distplot(posterior[500:], ax=ax, label='estimated posterior')
x = np.linspace(-.5, .5, 500)
post = calc_posterior_analytical(data, x, 0, 1)
ax.plot(x, post, 'g', label='analytic posterior')
_ = ax.set(xlabel='mu', ylabel='belief');
ax.legend();Аналитическое и оценочное апостериорные распределения вероятностей
Как можно заметить, следуя вышеописанному методу, мы получили сэмплы из того же распределения вероятностей, что было получено аналитическим путём.
Ширина диапазона для выборки предлагаемых значений
Выше мы задали интервал, из которого выбираются предлагаемые значения, равным 0,5. Именно это значение оказалось очень удачным. В общем случае, ширина диапазона не должна быть слишком маленькой, иначе сэмплинг будет неэффективным, так как для исследования пространства параметров понадобится слишком много времени и модель будет демонстрировать типичное для случайного блуждания поведение.
Вот, например, что мы получили, установив параметр proposal_width в значение 0,01.
▍Листинг 9
posterior_small = sampler(data, samples=5000, mu_init=1., proposal_width=.01)
fig, ax = plt.subplots()
ax.plot(posterior_small);
_ = ax.set(xlabel='sample', ylabel='mu');Результат использования слишком маленького диапазона
Слишком большой интервал тоже не подойдёт – предлагаемые для перехода значения будут постоянно отвергаться. Вот, что будет, если установить proposal_width в значение 3.
▍Листинг 10
posterior_large = sampler(data, samples=5000, mu_init=1., proposal_width=3.)
fig, ax = plt.subplots()
ax.plot(posterior_large); plt.xlabel('sample'); plt.ylabel('mu');
_ = ax.set(xlabel='sample', ylabel='mu');
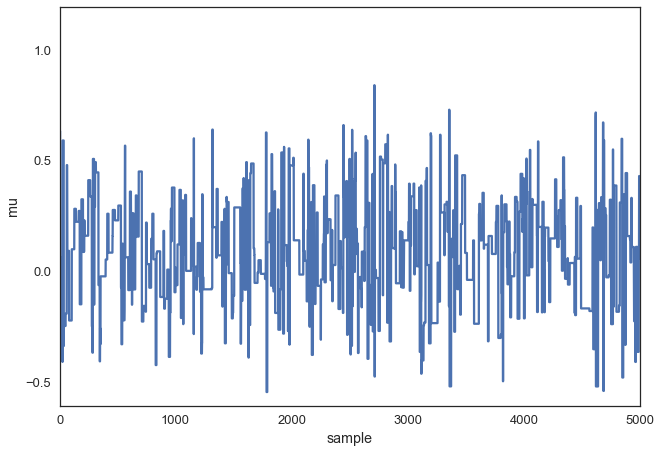
Результат использования слишком большого диапазона
Однако, обратите внимание на то, что мы здесь продолжаем брать сэмплы из целевого апостериорного распределения, как гарантирует математическое доказательство. Но такой подход менее эффективен.
▍Листинг 11
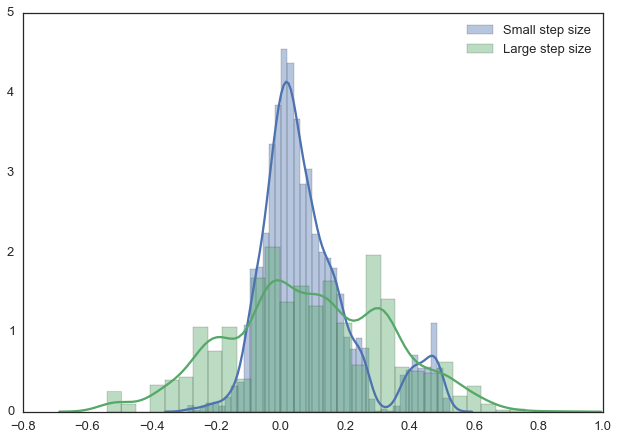
sns.distplot(posterior_small[1000:], label='Small step size')
sns.distplot(posterior_large[1000:], label='Large step size');
_ = plt.legend();
Маленький и большой размер шага
С использованием большого количества итераций, то, что у нас получится, в конечном счёте, будет выглядеть как настоящее апостериорное распределение. Главное то, что нам нужно, чтобы сэмплы были независимы друг от друга. В данном случае это, очевидно, не так. Для того, чтобы оценить эффективность нашего сэмплера, можно воспользоваться показателем автокорреляции. То есть – узнать, как образец i коррелирует с образцом i-1, i-2, и так далее.
▍Листинг 12
from pymc3.stats import autocorr
lags = np.arange(1, 100)
fig, ax = plt.subplots()
ax.plot(lags, [autocorr(posterior_large, l) for l in lags], label='large step size')
ax.plot(lags, [autocorr(posterior_small, l) for l in lags], label='small step size')
ax.plot(lags, [autocorr(posterior, l) for l in lags], label='medium step size')
ax.legend(loc=0)
_ = ax.set(xlabel='lag', ylabel='autocorrelation', ylim=(-.1, 1))Автокорреляция для маленького, среднего и большого размера шага
Очевидно то, что хотелось бы иметь интеллектуальный способ автоматического определения подходящего размера шага. Один из обычно используемых методов заключается в такой подстройке интервала, из которого выбирают значения, чтобы примерно 50% предложений отбрасывалось. Что интересно, другие алгоритмы MCMC, вроде Гибридного метода Монте-Карло (Hamiltonian Monte Carlo) очень похожи на тот, о котором мы говорили. Главная их особенность заключается в том, что они ведут себя «умнее», когда выдвигают предложения для следующего «прыжка».
Переходим к более сложным моделям
Теперь легко представить, что мы могли бы добавить параметр sigma для среднеквадратического отклонения и следовать той же процедуре для второго параметра. В таком случае генерировались бы предложения для mu и sigma, но логика алгоритма практически не изменилась бы. Или мы могли бы брать данные из очень разных распределений вероятностей, вроде биномиального, и, продолжая пользоваться тем же алгоритмом, получали бы правильное апостериорное распределение вероятностей. Это просто здорово, это – одно из огромных преимуществ вероятностного программирования: достаточно определить желаемую модель и позволить MCMC заниматься байесовским выводом.
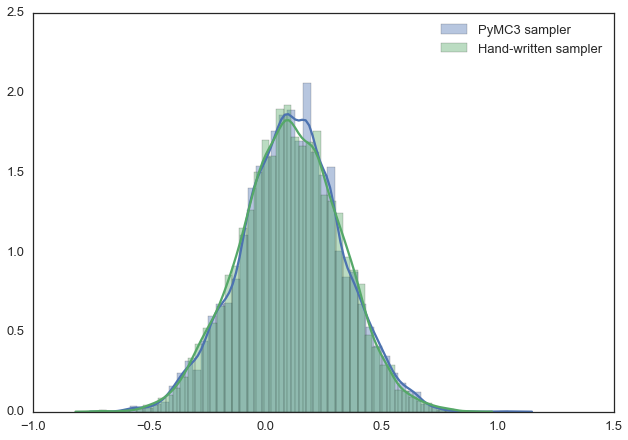
Вот, например, нижеприведённую модель можно очень легко описать средствами PyMC3. Так же, в этом примере мы пользуемся Метрополис-сэмплером (с автоматически настраиваемой шириной диапазона, из которого берутся предлагаемые значения) и видим, что результаты практически идентичны. Можете с этим поэкспериментировать, поменять распределение, например. В документации по PyMC3 можно найти более сложные примеры и сведения о том, как всё это работает.
▍Листинг 13
import pymc3 as pm
with pm.Model():
mu = pm.Normal('mu', 0, 1)
sigma = 1.
returns = pm.Normal('returns', mu=mu, sd=sigma, observed=data)
step = pm.Metropolis()
trace = pm.sample(15000, step)
sns.distplot(trace[2000:]['mu'], label='PyMC3 sampler');
sns.distplot(posterior[500:], label='Hand-written sampler');
plt.legend();Результаты работы различных сэмплеров
Подведём итоги
Надеемся, мы смогли донести до вас сущность MCMC, Метрополис-сэмплера, вероятностного вывода, и теперь у вас появилось интуитивное понимание всего этого. А значит – вы готовы к чтению материалов по данному вопросу, насыщенных математическими формулами. Там вы сможете найти все те детали, которые мы обошли здесь стороной для того, чтобы не скрыть за ними самого главного.
О, а приходите к нам работать? :)wunderfund.io — молодой фонд, который занимается высокочастотной алготорговлей. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Присоединяйтесь к нашей команде: wunderfund.io