Всем привет, меня зовут Фёдор Индукаев, я работаю аналитиком в Яндекс.Маршрутизации. Сегодня хочу рассказать вам про задачу визуализации пересекающихся множеств и про пакет для Python с открытым кодом, созданный мной для её решения. В процессе мы узнаем, чем различаются диаграммы Венна и Эйлера, познакомимся с сервисом распределения заказов и по касательной заденем такую область науки, как биоинформатика. Двигаться будем от простого к более сложному. Поехали!
Почти каждому, кто занимался разведочным анализом данных, хотя бы раз приходилось искать ответ на вопросы такого типа:

Все перечисленные вопросы можно свести к одной и той же формулировке. Она звучит так: даны несколько конечных множеств, возможно, пересекающихся между собой, и надо оценить их взаимное расположение — то есть понять, как именно они пересекаются.
Речь пойдёт о визуализациях и программных инструментах, помогающих решать эту задачу.
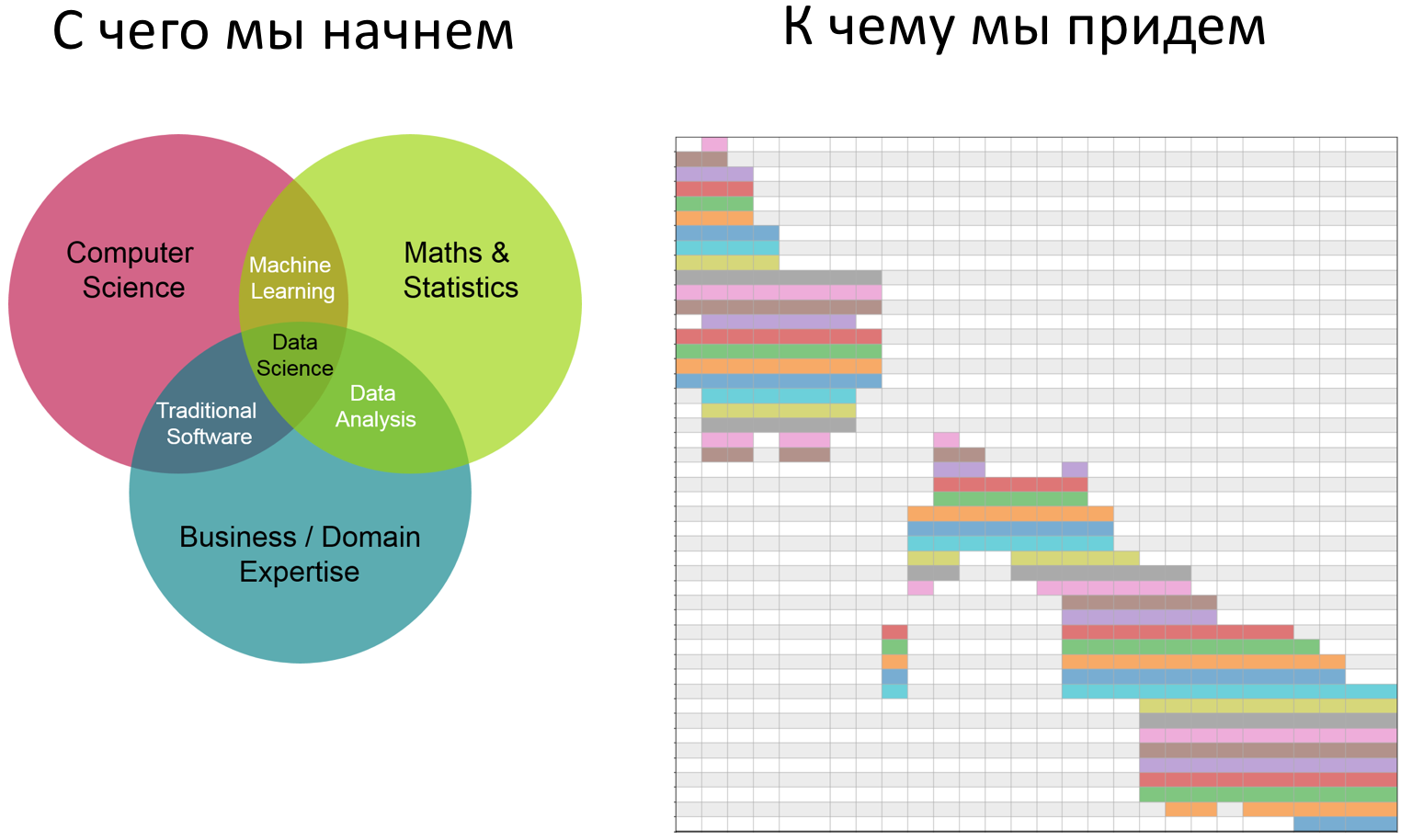
Такие рисунки с двумя или тремя кругами, думаю, знакомы каждому и не требуют объяснения:

Особенность диаграммы Венна в том, что она статична. Фигуры на ней равновелики и расположены симметрично. На рисунке изображаются все возможные пересечения, даже если большинство из них на самом деле пусты. Такие диаграммы подходят, чтобы проиллюстрировать абстрактные понятия или множества, точные размеры которых неизвестны либо неважны. Основная информация тут содержится не в графике, а в подписях.

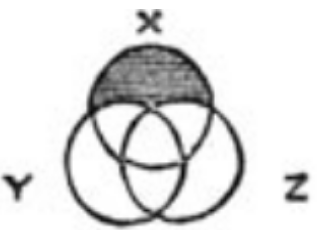 Именно такими их замыслил Джон Венн, английский математик и философ. В своей статье 1880 года он предложил диаграммы для графического отображения логических высказываний. К примеру, высказывание «любой Х — это Y либо Z» даёт диаграмму справа (иллюстрация взята из оригинальной статьи). Чёрным закрашена область, не удовлетворяющая высказыванию: те Х, которые не являются ни Y, ни Z. Основной посыл статьи именно в том, что статические рисунки без варьирования формы и расположения фигур лучше подходят для целей логики, чем динамические диаграммы Эйлера, о которых речь пойдёт ниже.
Именно такими их замыслил Джон Венн, английский математик и философ. В своей статье 1880 года он предложил диаграммы для графического отображения логических высказываний. К примеру, высказывание «любой Х — это Y либо Z» даёт диаграмму справа (иллюстрация взята из оригинальной статьи). Чёрным закрашена область, не удовлетворяющая высказыванию: те Х, которые не являются ни Y, ни Z. Основной посыл статьи именно в том, что статические рисунки без варьирования формы и расположения фигур лучше подходят для целей логики, чем динамические диаграммы Эйлера, о которых речь пойдёт ниже.
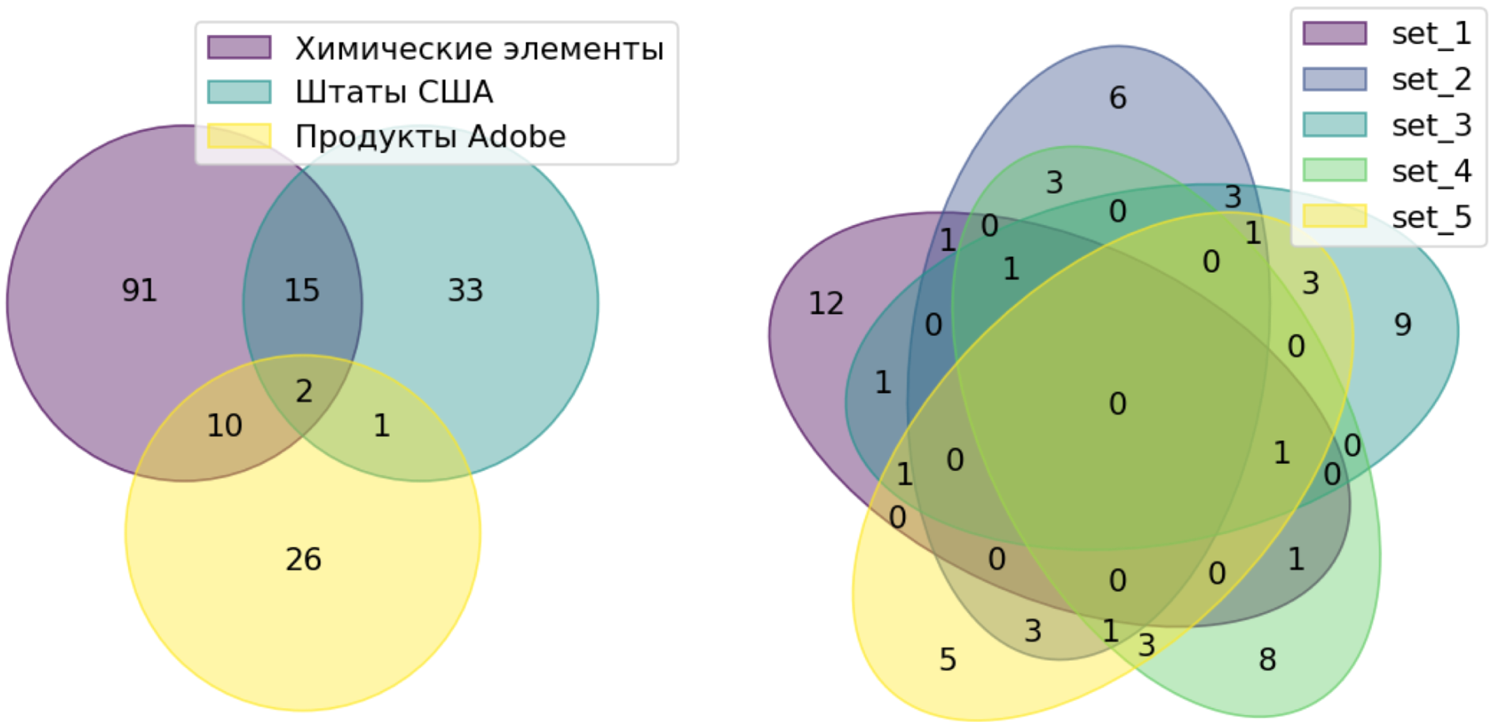
Ясно, что в анализе данных сфера применения диаграмм Венна ограничена. Они дают только качественную информацию, но не количественную и не отражают ни размер, ни даже пустоту пересечений. Если вас это не останавливает, в вашем распоряжении пакет venn, который строит такие диаграммы для множеств. Для каждого
множеств. Для каждого  там есть одна-две типовые картинки, и различаться будут только подписи:
там есть одна-две типовые картинки, и различаться будут только подписи:

Если же мы хотим что-то более динамически зависящее от данных, стоит обратить внимание на другой подход: диаграммы Эйлера.
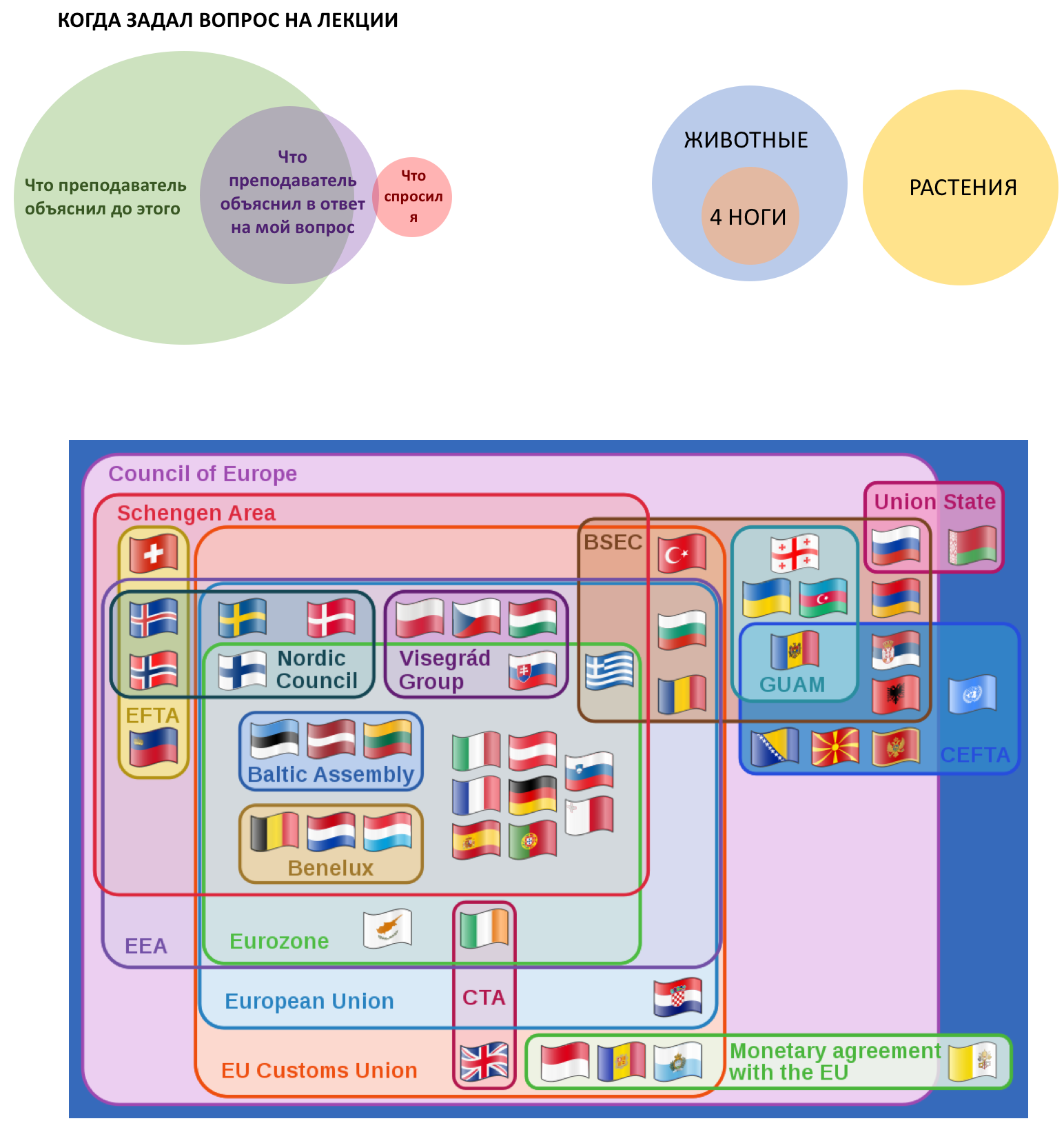
В отличие от диаграмм Венна, форма и положение фигур на плоскости здесь подобраны так, чтобы показать взаимоотношения множеств или понятий. Если какое-то пересечение пусто, то фигуры тоже по возможности не перекрывают друг друга, как на рисунке о растениях и животных.
Обратите внимание, что рисунок про вопрос на лекции отличается от остальных двух. На нём важно не только положение фигур, но и размеры пересечений — в них и заключен весь юмор.
Эту идею можно использовать и для нашей задачи. Возьмём два-три множества и нарисуем круги с площадями, пропорциональными размерам этих множеств. А затем постараемся расположить круги на плоскости таким образом, чтобы площади перекрытия также были пропорциональны размерам пересечений.
Именно это делает (несмотря на своё название) пакет matplotlib-venn:
Изобразить два множества с точным соблюдением всех пропорций легко. Но уже на трёх метод может давать сбой. Пусть, например, одно из трёх множеств — в точности пересечение остальных двух:

Рисунок выглядит неважно, появилась странная область с цифрой 0. Но удивляться тут нечему, ведь пересечение двух кругов изобразить в виде круга никак не получится.
А вот ещё более удручающий пример: два множества и их симметрическая разность (объединение минус пересечение):
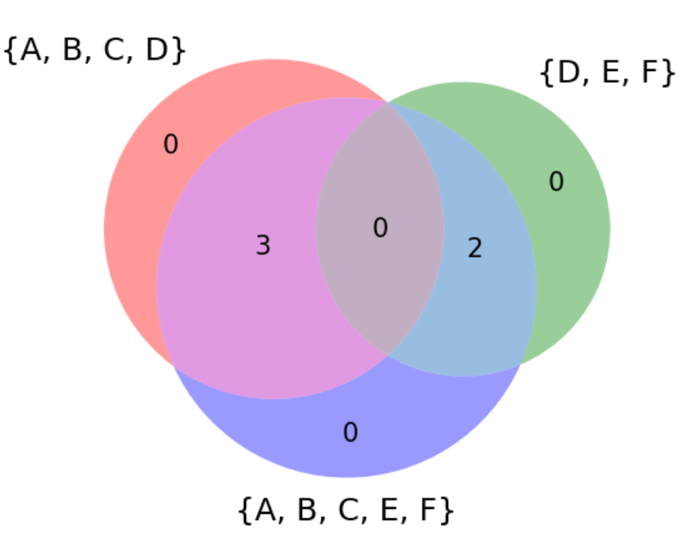
Получилось что-то совсем странное: обратите внимание, сколько тут нулей!
Первый пример ещё можно спасти, если взять вместо кругов прямоугольники (пересечение прямоугольников — тоже прямоугольник), а для второго нужны как минимум невыпуклые фигуры. Ну а больше трёх множеств данный пакет не поддерживает в принципе.
Других общедоступных инструментов для Python, развивающих подход Эйлера — Венна, я не знаю, и дальше пойдёт уже история моих собственных экспериментов. Но прежде чем продолжить, сделаю небольшое отступление, чтобы объяснить, зачем я вообще взялся за задачу визуализации множеств.
Как я говорил, наш отдел делает Яндекс.Маршрутизацию. Один из наших сервисов помогает интернет-магазинам, службам доставки и любым компаниям, чей бизнес включает логистику, строить оптимальные маршруты для транспорта.
Клиенты взаимодействуют с сервисом, отправляя запросы к API. Каждый запрос содержит список заказов (точек доставки) с координатами, интервалами доставки и т.д., а также список машин, которыми нужно развезти заказы. Наш алгоритм переваривает все эти данные и выдаёт оптимальные маршруты с учётом пробок, вместимости машин и много чего ещё.
У нас сотни, а не миллионы клиентов, как у популярных B2C-сервисов Яндекса. Поэтому нам особенно важно счастье каждого клиента, к тому же есть возможность уделять ему больше внимания и глубже погружаться в его задачи. Для этого, в частности, полезно иметь инструменты, помогающие понять, какие запросы нам присылает клиент.
Приведу пример. Допустим, за один день от компании «Ромашка» пришло 24 запроса. Это может означать, что:
Априори совершенно неясно, что из этого случилось на самом деле. Но если мы сможем быстро сравнить 24 множества ID заказов, ситуация сразу прояснится. Если они вообще не пересекаются — это первый случай (24 склада). Если множества перетекают одно в другое — второй (плановое обновление маршрутов). Ну а 24 почти одинаковых множества — возможный признак того, что клиенту надо помочь.
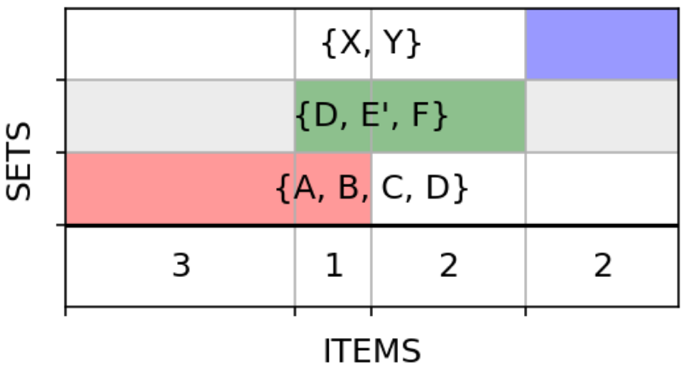
Какое-то время я пользовался пакетом matplotlib-venn, но ограничение в «два с половиной» множества, конечно, расстраивало. Размышляя над разными подходами к задаче, я решил попробовать перейти от кругов и вообще двумерных примитивов к одномерным — горизонтальным полосам. Пересечения тогда можно изображать наложением по вертикали вот таким образом:
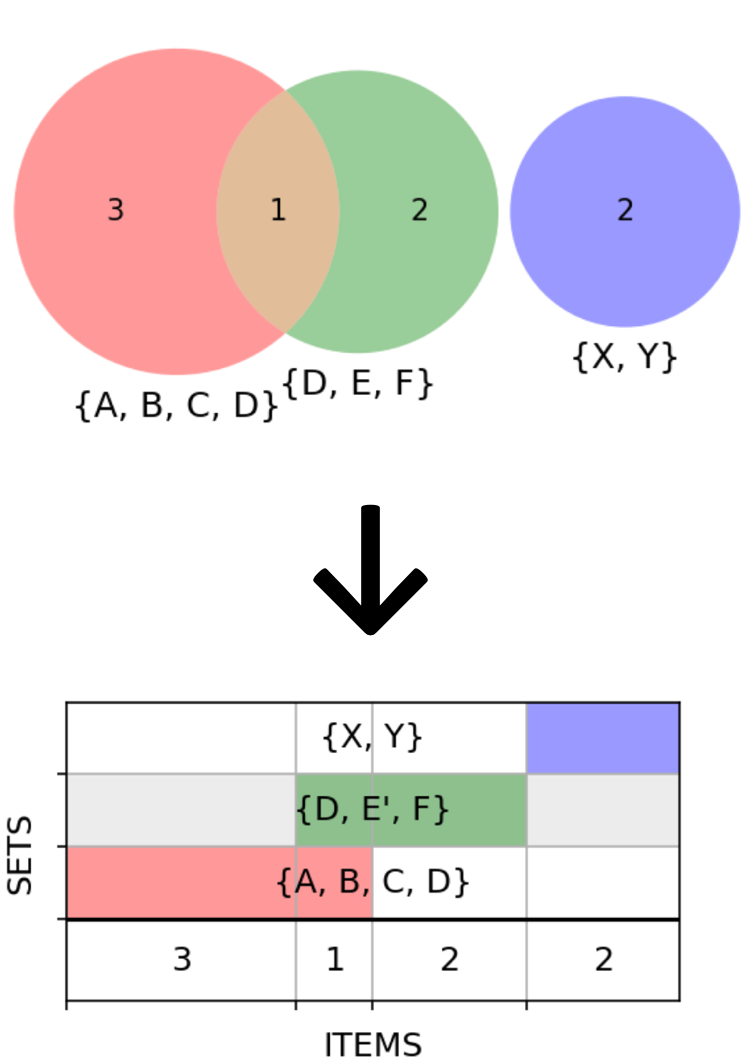
Линейные размеры воспринимаются глазом лучше, чем площади, для построения не нужна сложная тригонометрия, а разнесение множеств по оси Y делает график менее перегруженным. К тому же наш первый неудачный пример (два множества и их пересечение в качестве третьего) улучшается сам собой:
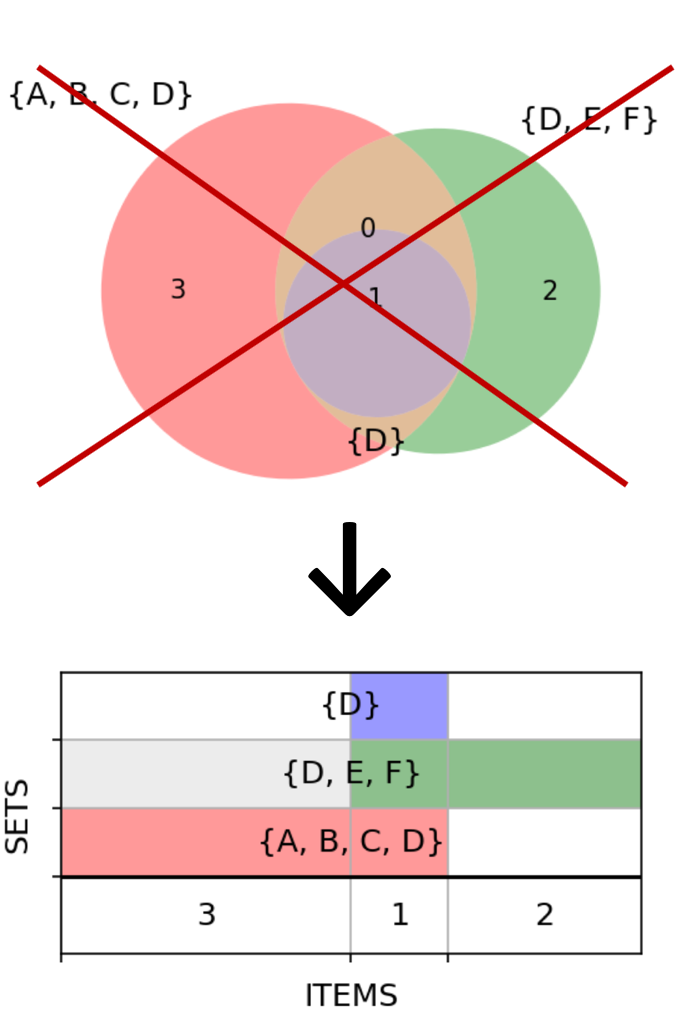
Проблема с симметрической разностью пока ещё никуда не делась. Но мы поступим с ней, как Александр Македонский с гордиевым узлом: разрешим, если надо, разрубать одно из множеств на две части:
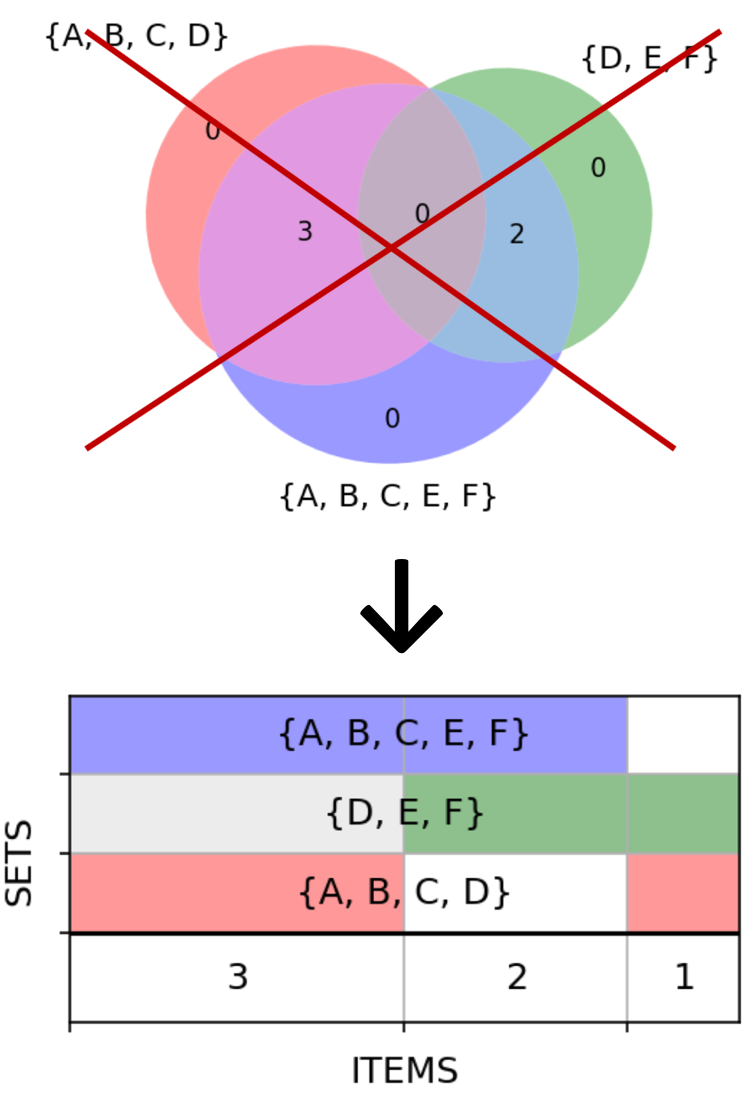
Красное множество изображено двумя полосами вместо одной, но ничего страшного в этом нет. Обе находятся на одной и той же высоте и имеют один цвет, так что их единство визуально хорошо считывается.
Нетрудно убедиться, что таким способом можно с точным соблюдением пропорций изобразить любые три множества. Тем самым задачу для равного 2 или 3 можно считать решённой.
равного 2 или 3 можно считать решённой.
Ещё один плюс такого подхода в том, что его легко применить к любому числу множеств, что мы и сделаем совсем скоро. Всё, что для этого нужно, — разрешить не один, а произвольное число разрывов в строках. Но сперва — немного простой комбинаторики.
Посмотрим на диаграмму Венна с тремя кругами и посчитаем, на сколько областей круги разбивают друг друга:

Каждая область определяется тем, лежит она внутри или снаружи каждого из трёх кругов, ну а внешняя область — лишняя. Итого получаем . Другие расположения трёх кругов могут давать меньшее количество областей вплоть до 1, когда все круги совпадают.
. Другие расположения трёх кругов могут давать меньшее количество областей вплоть до 1, когда все круги совпадают.
Перенося это рассуждение с кругов на множества, получим, что любые множеств разбивают друг друга не более чем на
множеств разбивают друг друга не более чем на  таких элементарных частей. Важно, что каждая из этих частей либо целиком входит, либо целиком не входит в любое из данных множеств. В наших новых диаграммах столбцы — это и есть такие элементарные части.
таких элементарных частей. Важно, что каждая из этих частей либо целиком входит, либо целиком не входит в любое из данных множеств. В наших новых диаграммах столбцы — это и есть такие элементарные части.
Итак, мы хотим обобщить вот такие схемы на случай :
:
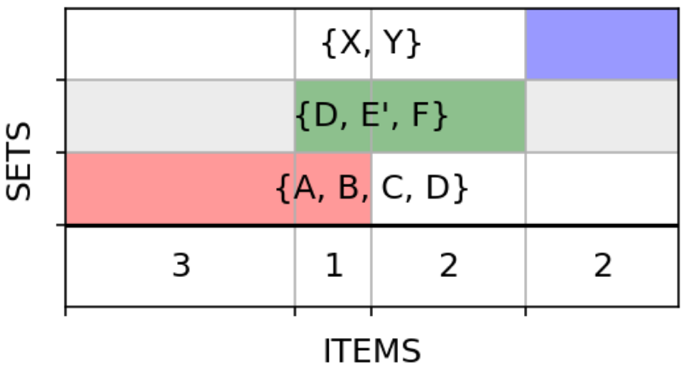
Для множеств у нас получается сетка с
множеств у нас получается сетка с  строками и
строками и  столбцами, как мы только что подсчитали. Остаётся пройтись по каждой строке и закрасить ячейки, соответствующие входящим в данное множество элементарным частям.
столбцами, как мы только что подсчитали. Остаётся пройтись по каждой строке и закрасить ячейки, соответствующие входящим в данное множество элементарным частям.
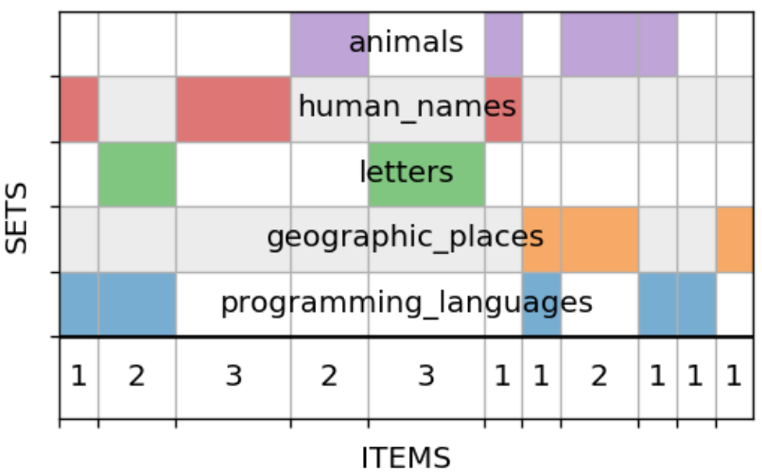
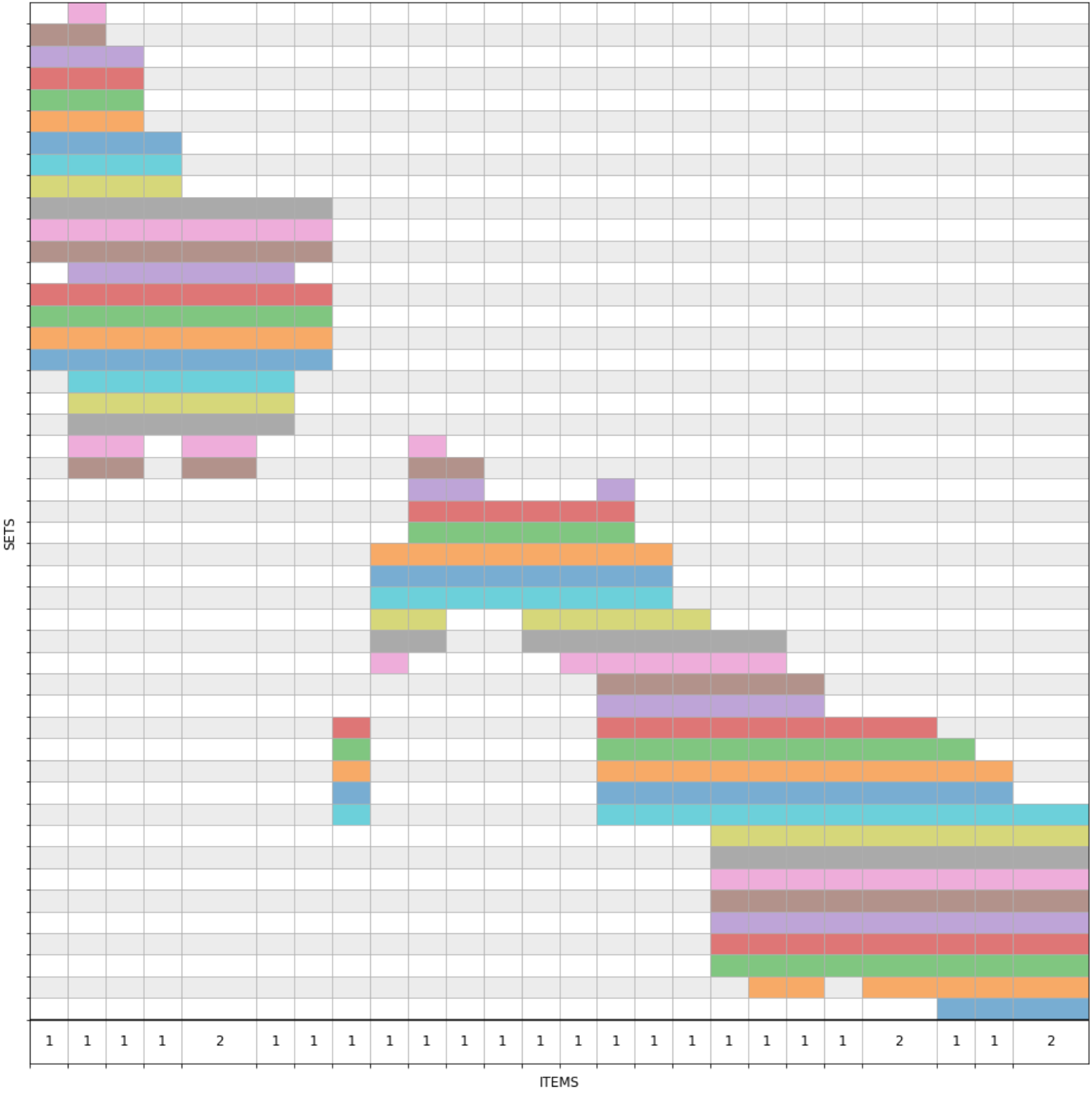
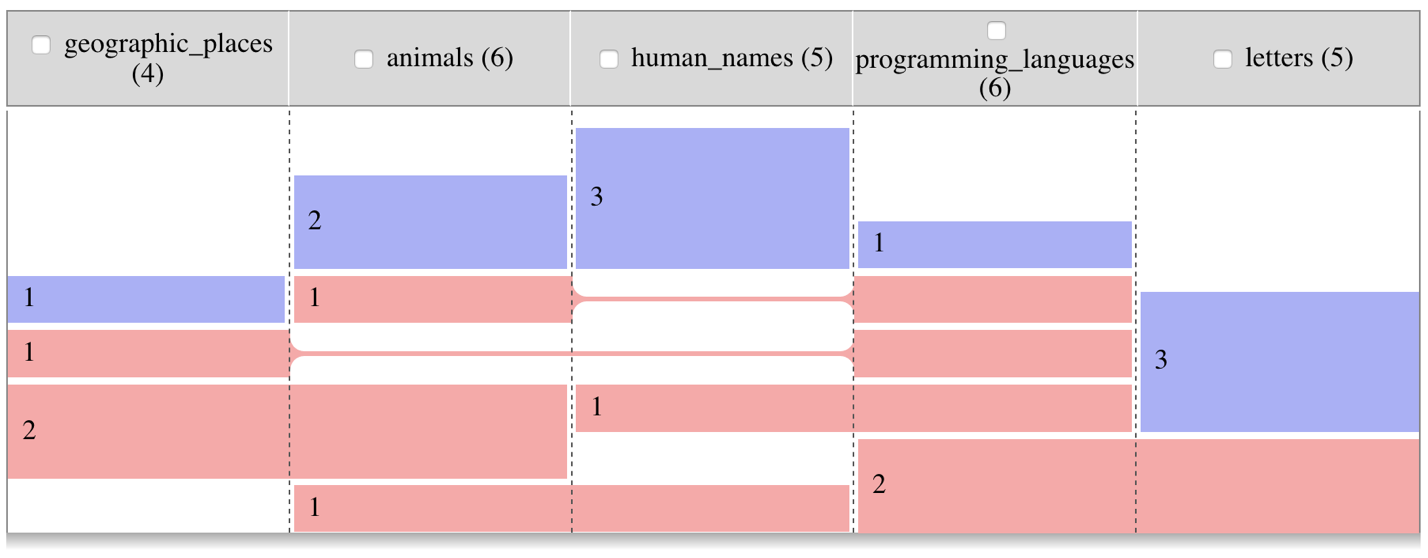
Для иллюстрации возьмём модельный пример с пятью множествами:
Действуя, как описано выше, получаем вот такой рисунок:
Читается он плохо: в строках слишком много разрывов, все множества порублены в капусту. Но раз нам не нравятся разрывы, то почему бы прямо не поставить задачу — минимизировать их? Ведь порядок столбцов несущественен, ничто не мешает нам переставлять их, как захочется. Приходим к такой задаче: найти перестановку столбцов данной матрицы из нулей и единиц с минимальным числом разрывов между единицами в строках.
Как мне подсказали уже позже, это практически задача коммивояжера в метрике Хэмминга, она NP-полная. Если столбцов получилось немного (скажем, не более 12), то найти нужную перестановку можно полным перебором, а иначе надо прибегать к тем или иным эвристикам.
Применим несложный жадный алгоритм. Назовём похожестью двух столбцов число позиций, на которых значения в этих столбцах совпадают. Возьмём два самых похожих столбца, поставим их вместе. Далее будем жадно наращивать последовательность в обе стороны от этой пары. Среди оставшихся столбцов найдём тот, который наиболее похож на один из этих двух, приставим — и так далее с остальными столбцами.
Вот рисунки до и после применения алгоритма:

Стало гораздо лучше. Именно на этой стадии я почувствовал, что выходит что-то полезное. Поэкспериментировав, я заметил, что алгоритм склонен залипать в локальных минимумах. Это удалось неплохо полечить с помощью простой рандомизации: немного зашумляем значения похожести столбцов, прогоняем алгоритм, повторяем 1000 раз, выбираем лучшее из 1000 решений.
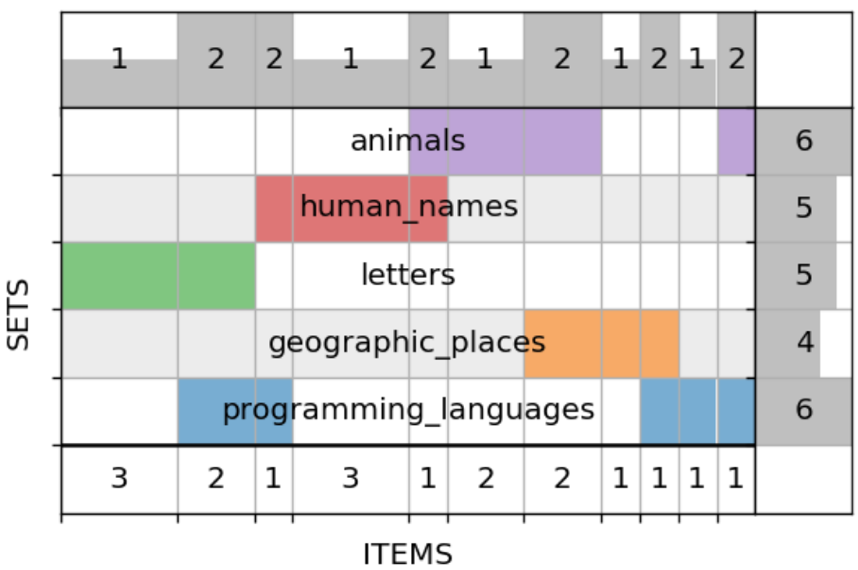
Получился уже вполне рабочий инструмент, но в него можно добавить ещё немного полезной информации. Я сделал два дополнительных графика: на правом выведены размеры исходных множеств, а верхний для каждого пересечения показывает, во сколько из наших множеств оно входит. По сути, это ни что иное, как суммы нашей бинарной матрицы по строкам (справа) и по столбцам (вверху):
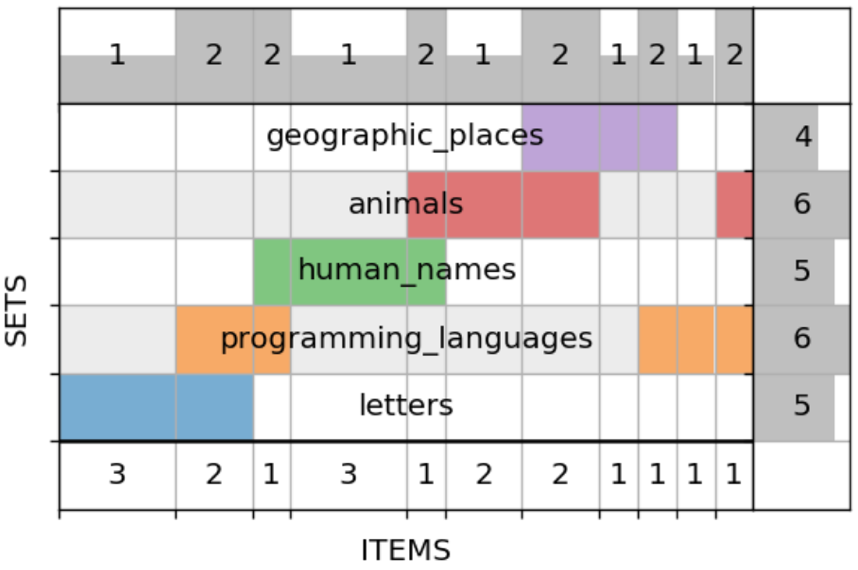
Ещё я добавил опцию упорядочивания самих множеств (т. е. строк) по тому же принципу, что и столбцов: с минимизацией числа разрывов. В итоге похожие множества группируются:
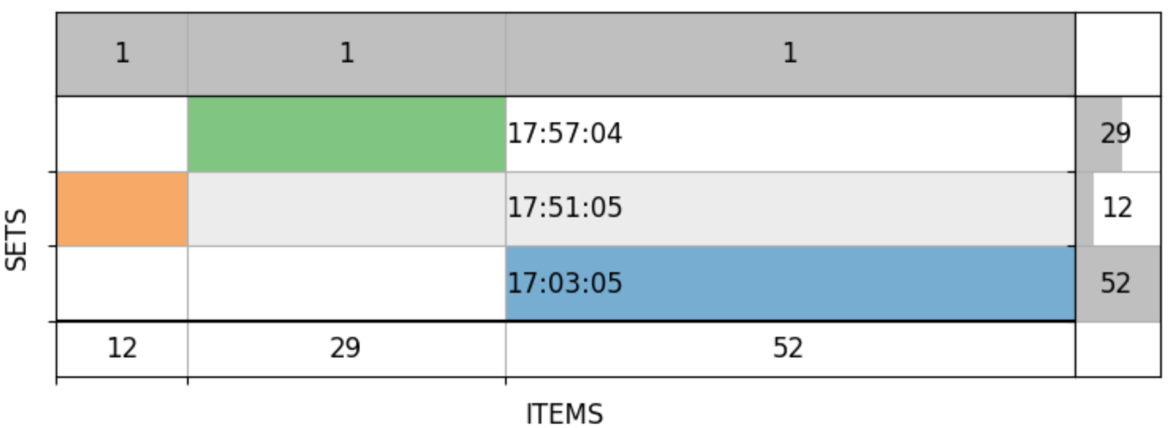
Естественно, первым делом я стал применять новый инструмент для той задачи, для которой его и создавал: исследовать запросы клиентов к нашему API. Результаты меня порадовали. Вот так, например, выглядел рабочий день одного из клиентов. Каждая строка — запрос к API (множество ID входящих в него заказов), а подписи в середине — время отправки запросов:

Весь день как на ладони. В 10:49 логист клиента с интервалом 23 секунды послал два одинаковых запроса со 129 заказами. С 11:25 до 15:53 было три запроса с другим набором из 152 заказов. В 16:43 пришёл третий уникальный запрос со 114 заказами. К решению этого запроса логист затем применил четыре ручные правки (это можно делать через наш UI).
А так выглядит идеальный день: все независимые задачи решены по одному разу, никаких правок или подбора параметров не потребовалось:
А вот пример от клиента, отправляющего запросы каждые 15–30 минут, чтобы учесть заказы, поступающие в реальном времени:
Даже на 50 множествах алгоритм хорошо выявил структуру, скрытую в данных. Видно, как старые заказы по мере исполнения убирались из запросов и замещались новыми.
Словом, закрыть созданным инструментом свою рабочую потребность мне вполне удалось.
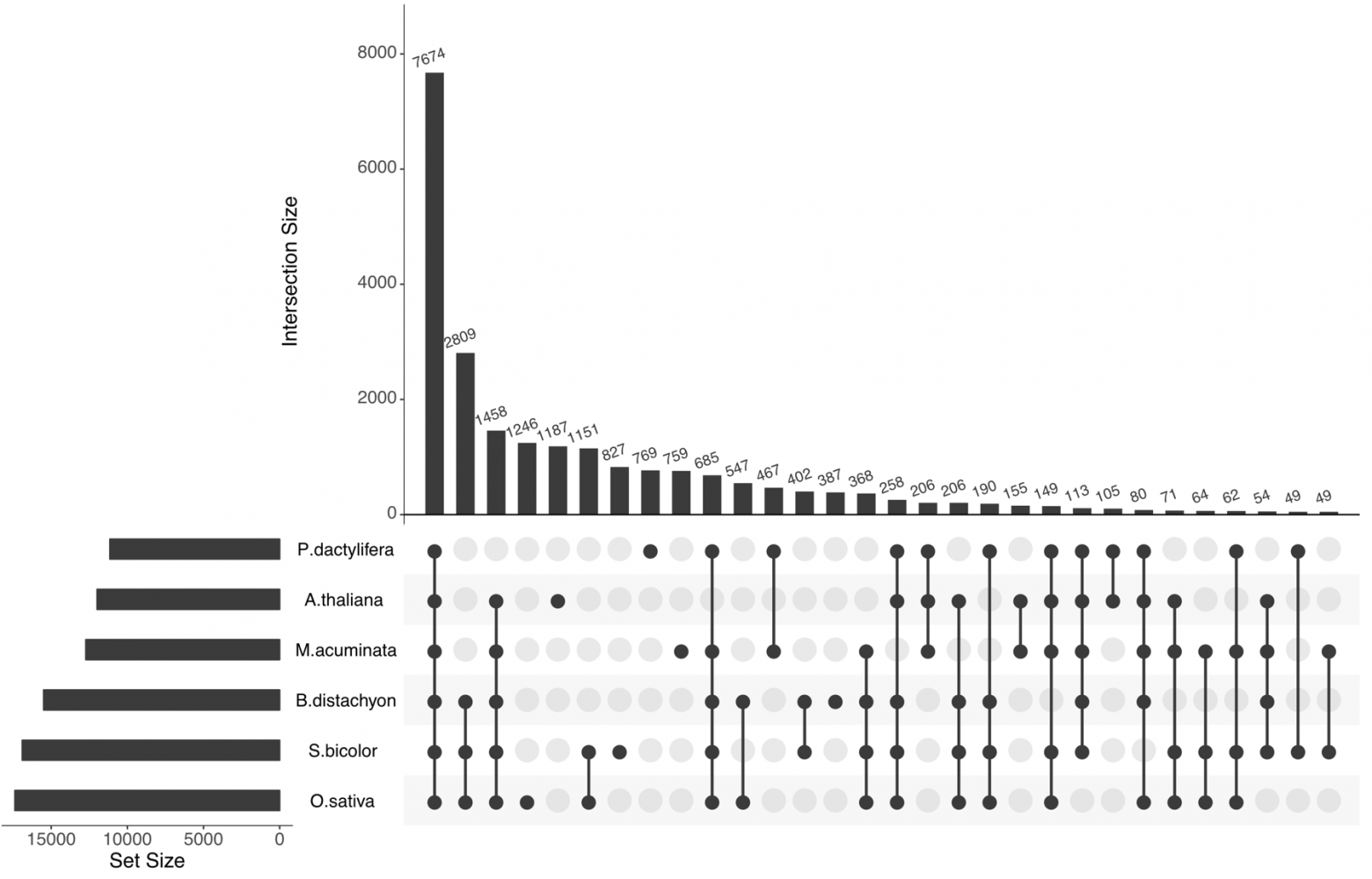
Пока я изучал существующие подходы, мне несколько раз попадался на глаза рисунок из журнала Nature, где сравниваются геномы банана и пяти других растений:

Обратите внимание, как соотносятся размеры областей с 13 и 149 элементами (указаны стрелками): вторая в несколько раз меньше. Так что ни о какой пропорциональности тут нет и речи.
Мне, конечно, захотелось попробовать силы и на таких данных, но результат меня не порадовал:

График выглядит неряшливо. Причина в том, что, во-первых, почти все пересечения (62 из 63 возможных) непусты, а во-вторых, их размеры различаются на три порядка. В результате числовым аннотациям становится очень тесно.
Чтобы мой инструмент был удобен и для таких данных, я добавил несколько параметров. Один позволяет частично выровнять ширины столбцов, другой прячет аннотации, если ширина столбца меньше заданной величины.

Такой вариант читается уже вполне неплохо, но ради этого пришлось пожертвовать точной пропорциональностью размеров.
Как оказалось, обратив внимание на сферу биоинформатики, я не прогадал. Я отправил пост о своём инструменте на Reddit в r/visualization, r/datascience и r/bioinformatics, именно в последнем его приняли лучше всего, отзывы были прямо-таки восторженные.
В итоге я понял, что получился неплохой инструмент, который может быть полезен многим. Поэтому родилась идея превратить его в полноценный пакет с открытым исходным кодом. Конечно, нужно было согласие руководителей, но ребята не только не возражали, но и поддержали меня, за что им большое спасибо.
Работая в основном по выходным, я начал понемногу приводить код в товарный вид, писать тесты и разбираться с системой пакетов в Python. Это мой первый проект такого рода, поэтому всё заняло несколько месяцев.
Придумать хорошее название тоже оказалось непростой задачей, и справился я с ней плоховато. Выбранное имя (supervenn) нельзя назвать удачным, ведь вся соль диаграмм Венна в их статичности, я же, напротив, стремился точно показывать реальные размеры. Но когда я это осознал, проект уже вышел в свет и менять название было поздно.
Конечно, я не первый использовал этот подход к визуализации множеств: идея, в общем-то, лежит на поверхности. В открытом доступе есть два похожих веб-приложения: RainBio и Linear Diagram Generator, второе использует в точности тот же принцип, что и у меня. (Авторы вдобавок написали статью на 40 страниц, где экспериментально сравнили, что лучше воспринимается — горизонтальные или вертикальные линии, тонкие или толстые и т. п. Мне даже показалось, что для них первичной была именно статья, а сам инструмент — лишь дополнение к ней.)
Чтобы сравнить эти два приложения с моим пакетом, снова используем пример со словами. Можете сами решить, какой вариант более удобочитаем и информативен.
RainBio
Linear Diagram Generator

supervenn

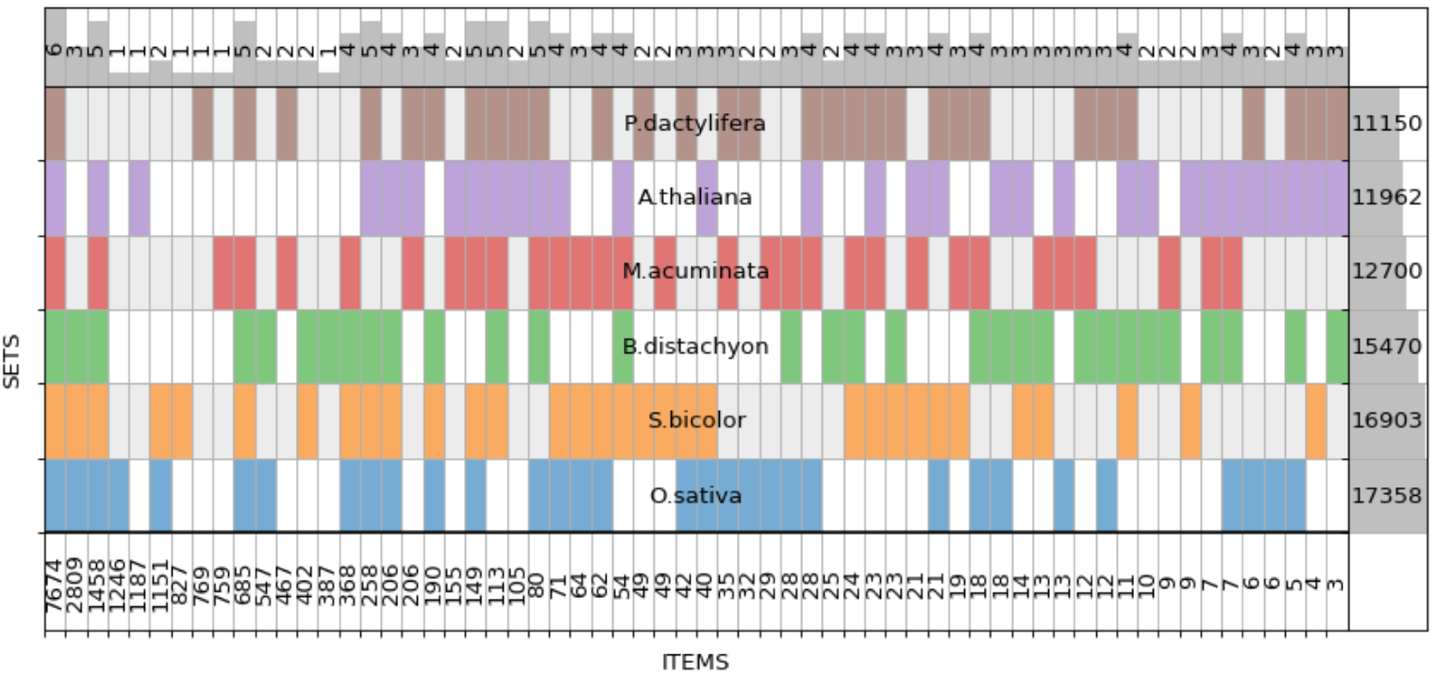
Нельзя не упомянуть проект UpSet, существующий в виде веб-приложения и пакетов для R и Python. Базовый принцип можно понять, посмотрев на отображение данных о геноме банана. График обрезан справа, показаны только 30 пересечений из 62:
Интересно, что если использовать supervenn с сортировкой столбцов по ширине и сделать столбцы одинаковыми с помощью параметра выравнивания ширин, то получится почти то же самое, хотя это и не сразу заметно. Не хватает лишь вертикальных линий с размерами пересечений, вместо них только цифры внизу графика:
Уже при написании этого текста я попробовал воспользоваться Python-версией UpSet, но обнаружил, что пакет не обновлялся с 2016 года, в документации никак не описан формат входных данных, а тестовый пример падает с ошибкой. Веб-версия исправна, в ней много полезных вспомогательных функций, но работать с ней довольно тяжело из-за сложного способа ввода данных.
Наконец, в сети доступен интересный обзор методов визуализации множеств. Далеко не все из них реализованы в виде программных инструментов. Вот несколько картинок для привлечения внимания:
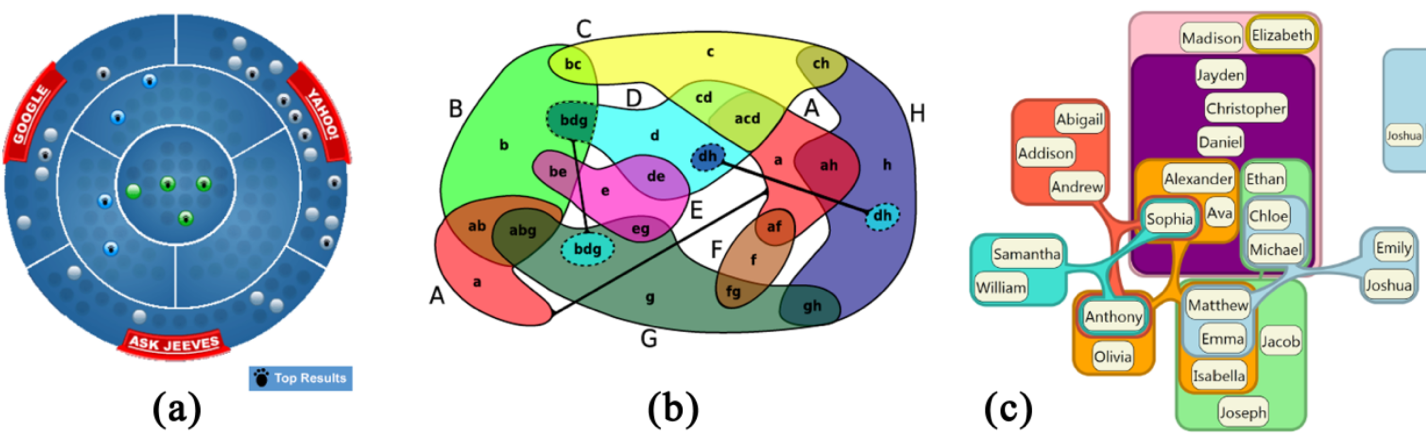
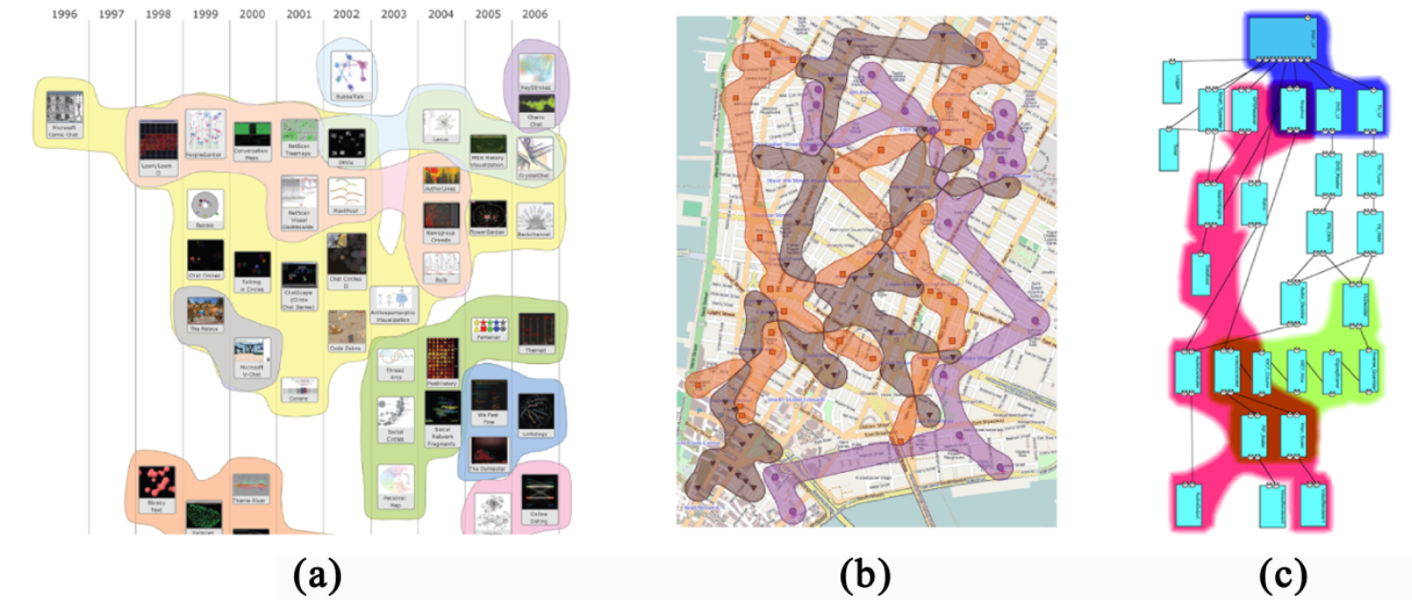
Особенно меня заинтересовал метод Bubble Sets (нижний ряд), позволяющий изображать небольшие множества поверх заданного расположения элементов на плоскости. Это может быть удобно, например, когда элементы привязаны к оси времени (а) или к карте (b). Пока что этот метод реализован только на Java и JavaScript (ссылки есть на странице авторов), и было бы здорово, если бы кто-нибудь взялся портировать его на Python.
Я отправил письма с кратким описанием проекта авторам UpSet и обзора и получил хорошие отзывы. Двое из них даже обещали включить supervenn в свои лекции по визуализации множеств.
Если вы захотите воспользоваться пакетом, он доступен на GitHub и в PyPI: pip install supervenn. Я буду благодарен за любые замечания о коде и использовании пакета, за идеи и критику. Особенно буду рад прочитать рекомендации, как улучшить алгоритм перестановки столбцов для больших , и советы, как писать тесты для функций построения графиков.
, и советы, как писать тесты для функций построения графиков.
Спасибо за внимание!
1. John Venn. On the diagrammatic and mechanical representation of propositions and reasonings. The London, Edinburgh and Dublin Philosophical Magazine, July 1880.
2. J.-B. Lamy and R. Tsopra. RainBio: Proportional visualization of large sets in biology. IEEE Transactions on Visualization and Computer Graphics, doi: 10.1109/TVCG.2019.2921544.
3. Peter Rodgers, Gem Stapleton and Peter Chapman. Visualizing Sets with Linear Diagrams. ACM Transactions on Computer Human Interaction 22(6) pp. 27:1-27:39 September 2015. doi:10.1145/2810012.
4. Alexander Lex, Nils Gehlenborg, Hendrik Strobelt, Romain Vuillemot, Hanspeter Pfister
UpSet: Visualization of Intersecting Sets. IEEE Transactions on Visualization and Computer Graphics (InfoVis’14), 2014.
5. Bilal Alsallakh, Luana Micallef, Wolfgang Aigner, Helwig Hauser, Silvia Miksch and Peter Rodgers. The State-of-the-Art of Set Visualization. Computer Graphics Forum. Volume 00 (2015), number 0 pp. 1–27 10.1111/cgf.12722.
6. Christopher Collins, Gerald Penn and Sheelagh Carpendale. Bubble Sets: Revealing Set Relations with Isocontours over Existing Visualizations. IEEE Trans. on Visualization and Computer Graphics (Proc. of the IEEE Conf. on Information Visualization), vol. 15, iss. 6, pp. 1009−1016, 2009.
О чём речь и зачем это нужно?
Почти каждому, кто занимался разведочным анализом данных, хотя бы раз приходилось искать ответ на вопросы такого типа:
- Есть датасет с несколькими независимыми бинарными переменными. Какие из них часто встречаются вместе?
- Есть несколько таблиц с объектами одной природы, имеющими ID. Как соотносятся множества ID из разных таблиц — то ли в каждой таблице свои ID, то ли во всех таблицах одни и те же, то ли наборы отличаются, но незначительно?
- Есть несколько биологических видов. У каких организмов похожи наборы генов или белков?
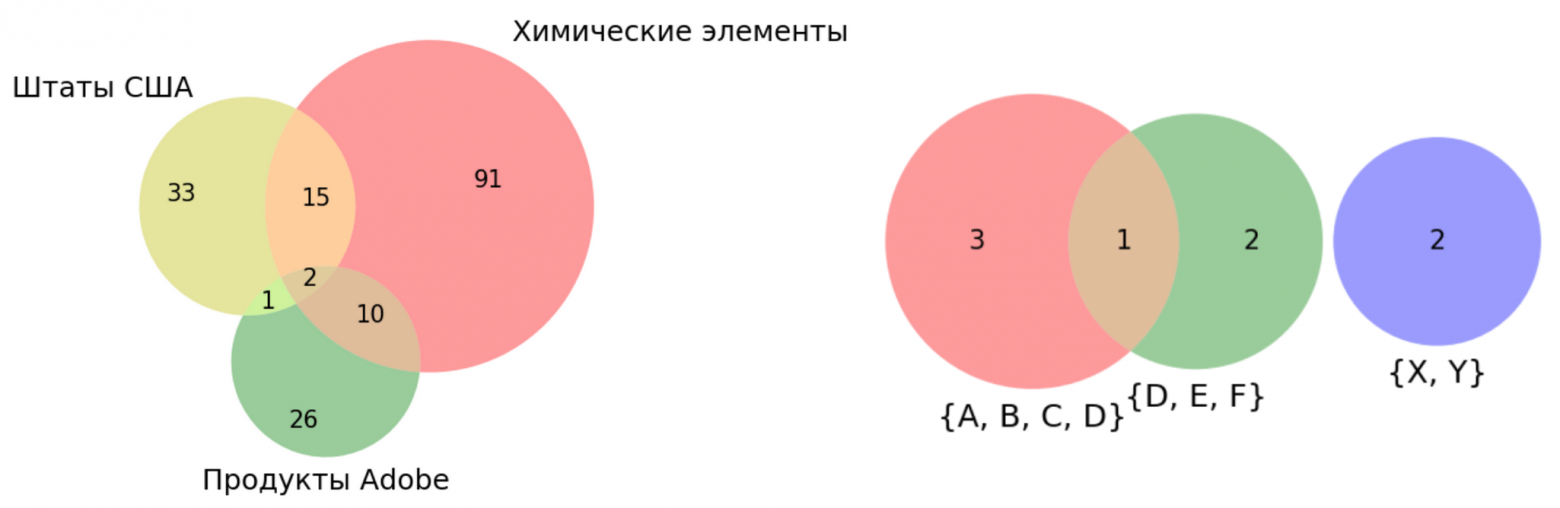
- Как построить график наподобие pie chart, если категории пересекаются? (Правда, это становится проблемой не для всех: см. процентные значения на рисунке ниже.)
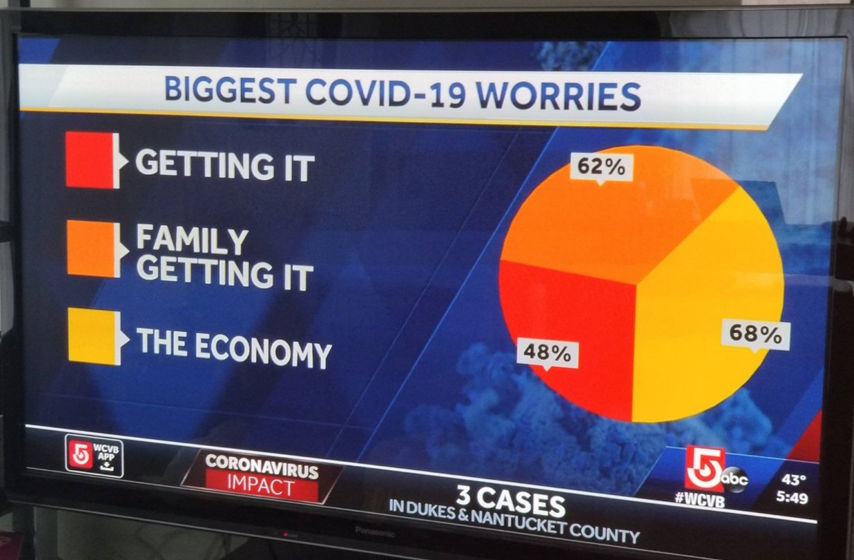
Все перечисленные вопросы можно свести к одной и той же формулировке. Она звучит так: даны несколько конечных множеств, возможно, пересекающихся между собой, и надо оценить их взаимное расположение — то есть понять, как именно они пересекаются.
Речь пойдёт о визуализациях и программных инструментах, помогающих решать эту задачу.
Диаграммы Венна
Такие рисунки с двумя или тремя кругами, думаю, знакомы каждому и не требуют объяснения:

Особенность диаграммы Венна в том, что она статична. Фигуры на ней равновелики и расположены симметрично. На рисунке изображаются все возможные пересечения, даже если большинство из них на самом деле пусты. Такие диаграммы подходят, чтобы проиллюстрировать абстрактные понятия или множества, точные размеры которых неизвестны либо неважны. Основная информация тут содержится не в графике, а в подписях.

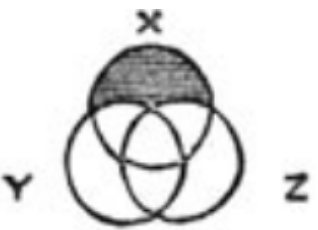 Именно такими их замыслил Джон Венн, английский математик и философ. В своей статье 1880 года он предложил диаграммы для графического отображения логических высказываний. К примеру, высказывание «любой Х — это Y либо Z» даёт диаграмму справа (иллюстрация взята из оригинальной статьи). Чёрным закрашена область, не удовлетворяющая высказыванию: те Х, которые не являются ни Y, ни Z. Основной посыл статьи именно в том, что статические рисунки без варьирования формы и расположения фигур лучше подходят для целей логики, чем динамические диаграммы Эйлера, о которых речь пойдёт ниже.
Именно такими их замыслил Джон Венн, английский математик и философ. В своей статье 1880 года он предложил диаграммы для графического отображения логических высказываний. К примеру, высказывание «любой Х — это Y либо Z» даёт диаграмму справа (иллюстрация взята из оригинальной статьи). Чёрным закрашена область, не удовлетворяющая высказыванию: те Х, которые не являются ни Y, ни Z. Основной посыл статьи именно в том, что статические рисунки без варьирования формы и расположения фигур лучше подходят для целей логики, чем динамические диаграммы Эйлера, о которых речь пойдёт ниже.Ясно, что в анализе данных сфера применения диаграмм Венна ограничена. Они дают только качественную информацию, но не количественную и не отражают ни размер, ни даже пустоту пересечений. Если вас это не останавливает, в вашем распоряжении пакет venn, который строит такие диаграммы для
Если же мы хотим что-то более динамически зависящее от данных, стоит обратить внимание на другой подход: диаграммы Эйлера.
Диаграммы Эйлера
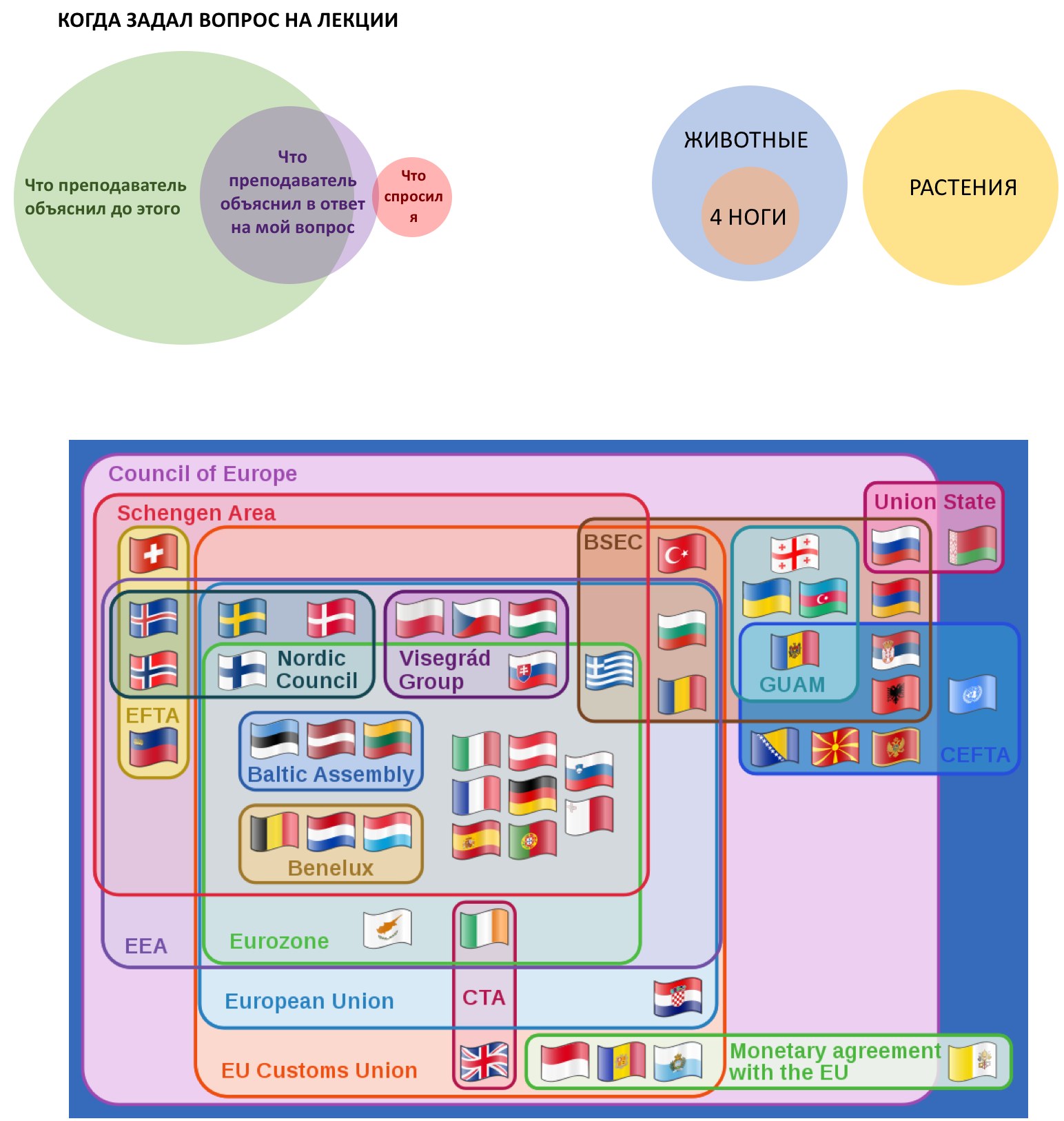
В отличие от диаграмм Венна, форма и положение фигур на плоскости здесь подобраны так, чтобы показать взаимоотношения множеств или понятий. Если какое-то пересечение пусто, то фигуры тоже по возможности не перекрывают друг друга, как на рисунке о растениях и животных.
Обратите внимание, что рисунок про вопрос на лекции отличается от остальных двух. На нём важно не только положение фигур, но и размеры пересечений — в них и заключен весь юмор.
Эту идею можно использовать и для нашей задачи. Возьмём два-три множества и нарисуем круги с площадями, пропорциональными размерам этих множеств. А затем постараемся расположить круги на плоскости таким образом, чтобы площади перекрытия также были пропорциональны размерам пересечений.
Именно это делает (несмотря на своё название) пакет matplotlib-venn:
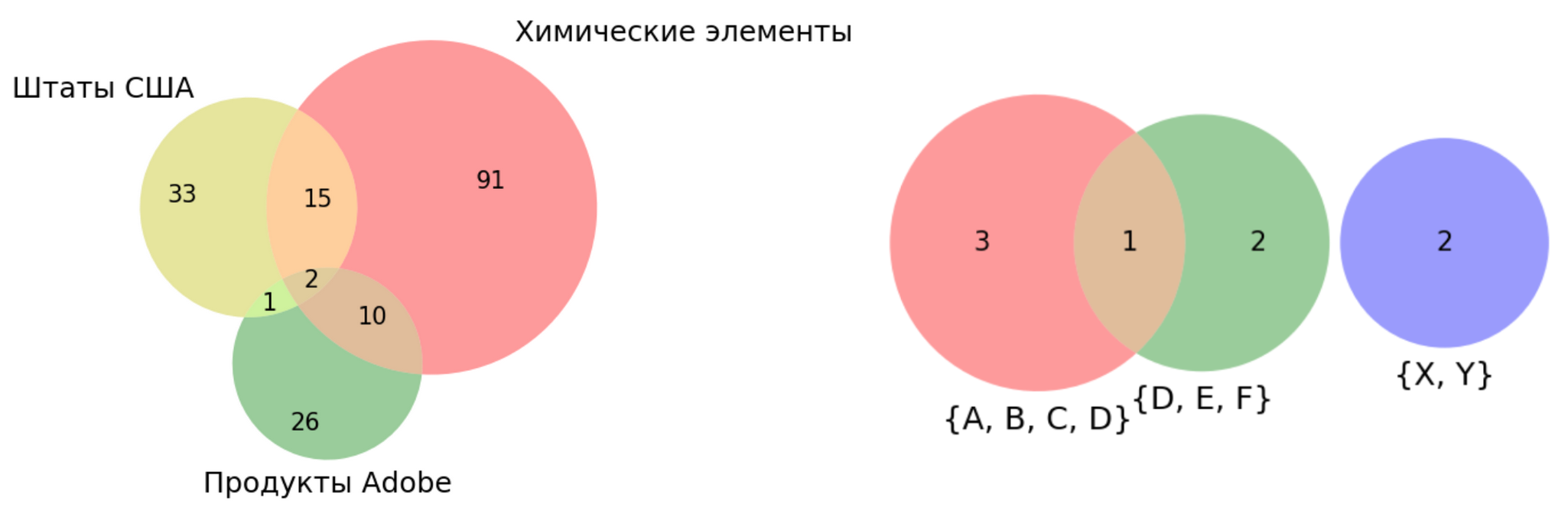
Изобразить два множества с точным соблюдением всех пропорций легко. Но уже на трёх метод может давать сбой. Пусть, например, одно из трёх множеств — в точности пересечение остальных двух:
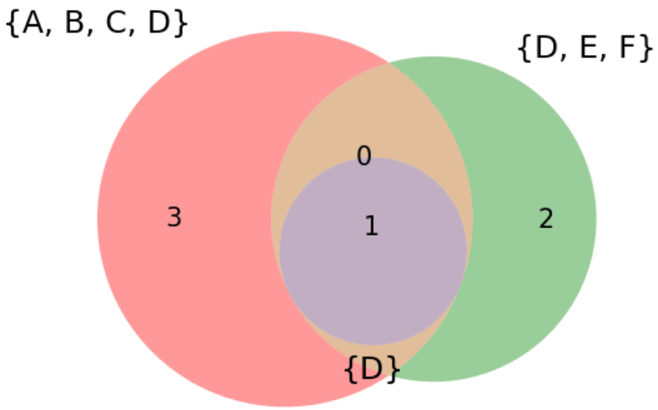
Рисунок выглядит неважно, появилась странная область с цифрой 0. Но удивляться тут нечему, ведь пересечение двух кругов изобразить в виде круга никак не получится.
А вот ещё более удручающий пример: два множества и их симметрическая разность (объединение минус пересечение):

Получилось что-то совсем странное: обратите внимание, сколько тут нулей!
Первый пример ещё можно спасти, если взять вместо кругов прямоугольники (пересечение прямоугольников — тоже прямоугольник), а для второго нужны как минимум невыпуклые фигуры. Ну а больше трёх множеств данный пакет не поддерживает в принципе.
Других общедоступных инструментов для Python, развивающих подход Эйлера — Венна, я не знаю, и дальше пойдёт уже история моих собственных экспериментов. Но прежде чем продолжить, сделаю небольшое отступление, чтобы объяснить, зачем я вообще взялся за задачу визуализации множеств.
Пару слов об API построения оптимальных маршрутов
Как я говорил, наш отдел делает Яндекс.Маршрутизацию. Один из наших сервисов помогает интернет-магазинам, службам доставки и любым компаниям, чей бизнес включает логистику, строить оптимальные маршруты для транспорта.
Клиенты взаимодействуют с сервисом, отправляя запросы к API. Каждый запрос содержит список заказов (точек доставки) с координатами, интервалами доставки и т.д., а также список машин, которыми нужно развезти заказы. Наш алгоритм переваривает все эти данные и выдаёт оптимальные маршруты с учётом пробок, вместимости машин и много чего ещё.
У нас сотни, а не миллионы клиентов, как у популярных B2C-сервисов Яндекса. Поэтому нам особенно важно счастье каждого клиента, к тому же есть возможность уделять ему больше внимания и глубже погружаться в его задачи. Для этого, в частности, полезно иметь инструменты, помогающие понять, какие запросы нам присылает клиент.
Приведу пример. Допустим, за один день от компании «Ромашка» пришло 24 запроса. Это может означать, что:
- Они работают по всей стране и построили 24 набора маршрутов для 24 складов.
- Склад всего один, но клиенту постоянно поступают новые заказы. Чтобы их учесть, надо каждый час обновлять маршруты.
- Запросы у клиента формируются с ошибкой, из-за которой он 24 раза подряд не смог получить хорошее решение одной-единственной задачи.
Априори совершенно неясно, что из этого случилось на самом деле. Но если мы сможем быстро сравнить 24 множества ID заказов, ситуация сразу прояснится. Если они вообще не пересекаются — это первый случай (24 склада). Если множества перетекают одно в другое — второй (плановое обновление маршрутов). Ну а 24 почти одинаковых множества — возможный признак того, что клиенту надо помочь.
Упрощаем задачу: от кругов к полосам
Какое-то время я пользовался пакетом matplotlib-venn, но ограничение в «два с половиной» множества, конечно, расстраивало. Размышляя над разными подходами к задаче, я решил попробовать перейти от кругов и вообще двумерных примитивов к одномерным — горизонтальным полосам. Пересечения тогда можно изображать наложением по вертикали вот таким образом:
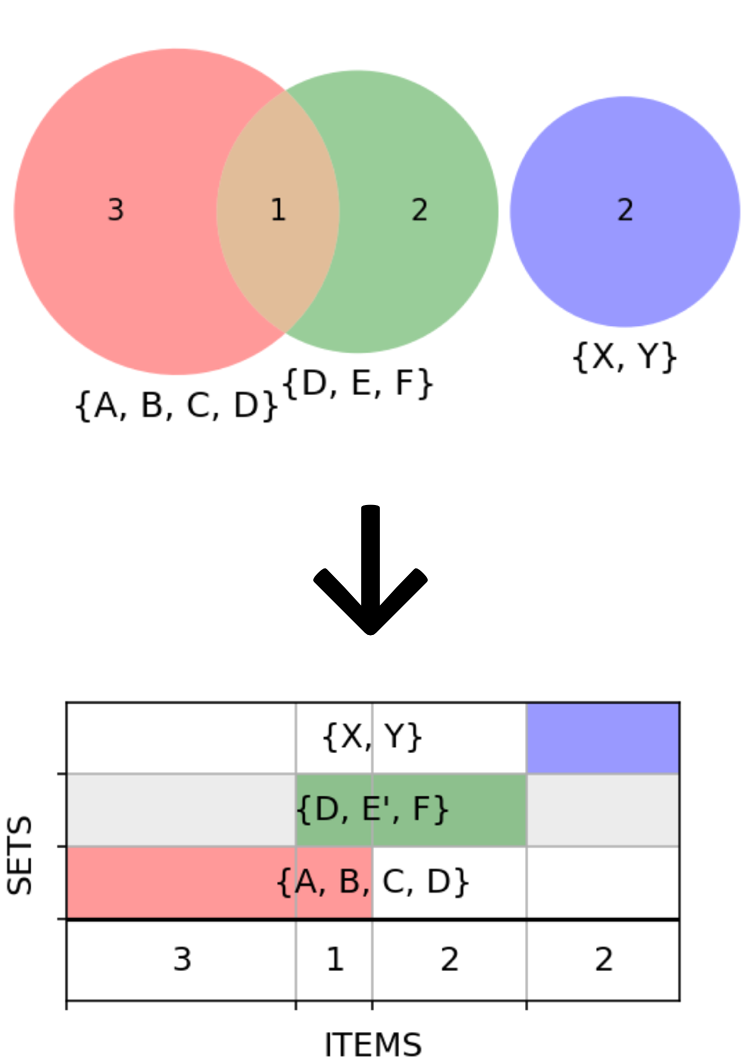
Линейные размеры воспринимаются глазом лучше, чем площади, для построения не нужна сложная тригонометрия, а разнесение множеств по оси Y делает график менее перегруженным. К тому же наш первый неудачный пример (два множества и их пересечение в качестве третьего) улучшается сам собой:

Проблема с симметрической разностью пока ещё никуда не делась. Но мы поступим с ней, как Александр Македонский с гордиевым узлом: разрешим, если надо, разрубать одно из множеств на две части:
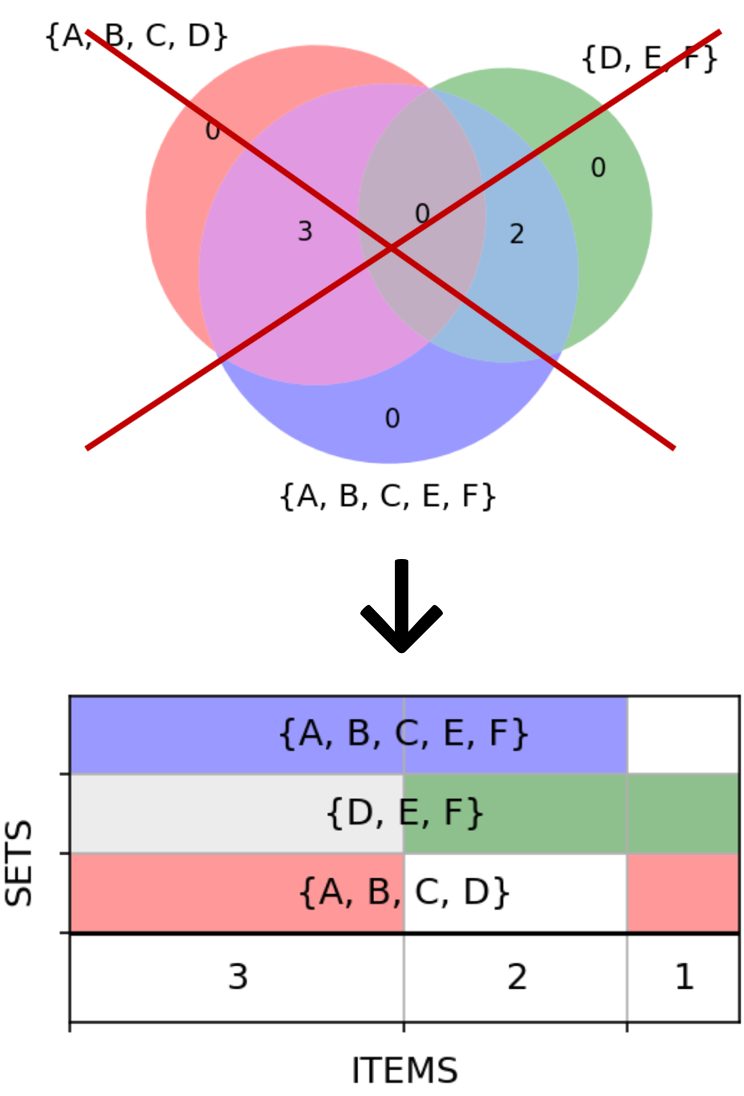
Красное множество изображено двумя полосами вместо одной, но ничего страшного в этом нет. Обе находятся на одной и той же высоте и имеют один цвет, так что их единство визуально хорошо считывается.
Нетрудно убедиться, что таким способом можно с точным соблюдением пропорций изобразить любые три множества. Тем самым задачу для
Ещё один плюс такого подхода в том, что его легко применить к любому числу множеств, что мы и сделаем совсем скоро. Всё, что для этого нужно, — разрешить не один, а произвольное число разрывов в строках. Но сперва — немного простой комбинаторики.
Немного арифметики
Посмотрим на диаграмму Венна с тремя кругами и посчитаем, на сколько областей круги разбивают друг друга:
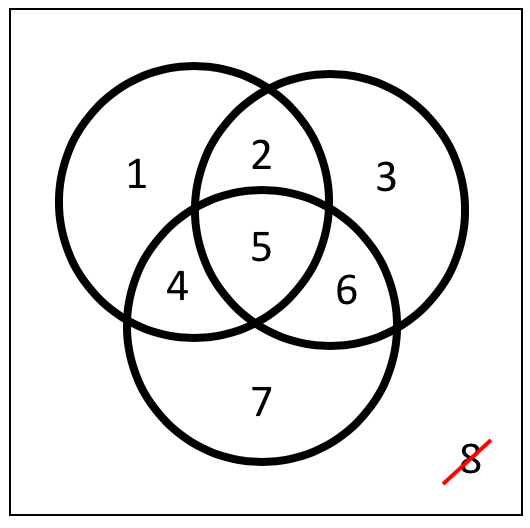
Каждая область определяется тем, лежит она внутри или снаружи каждого из трёх кругов, ну а внешняя область — лишняя. Итого получаем
Перенося это рассуждение с кругов на множества, получим, что любые
Больше множеств!
Итак, мы хотим обобщить вот такие схемы на случай
Для
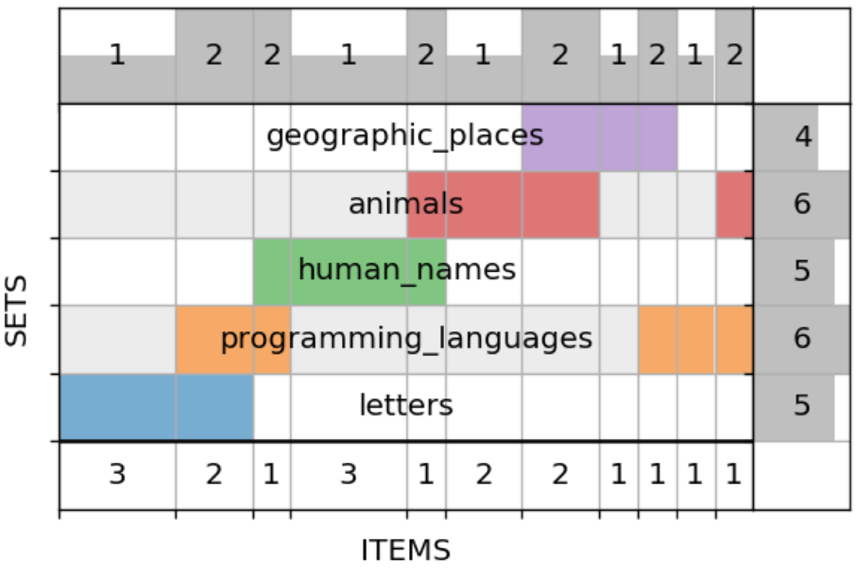
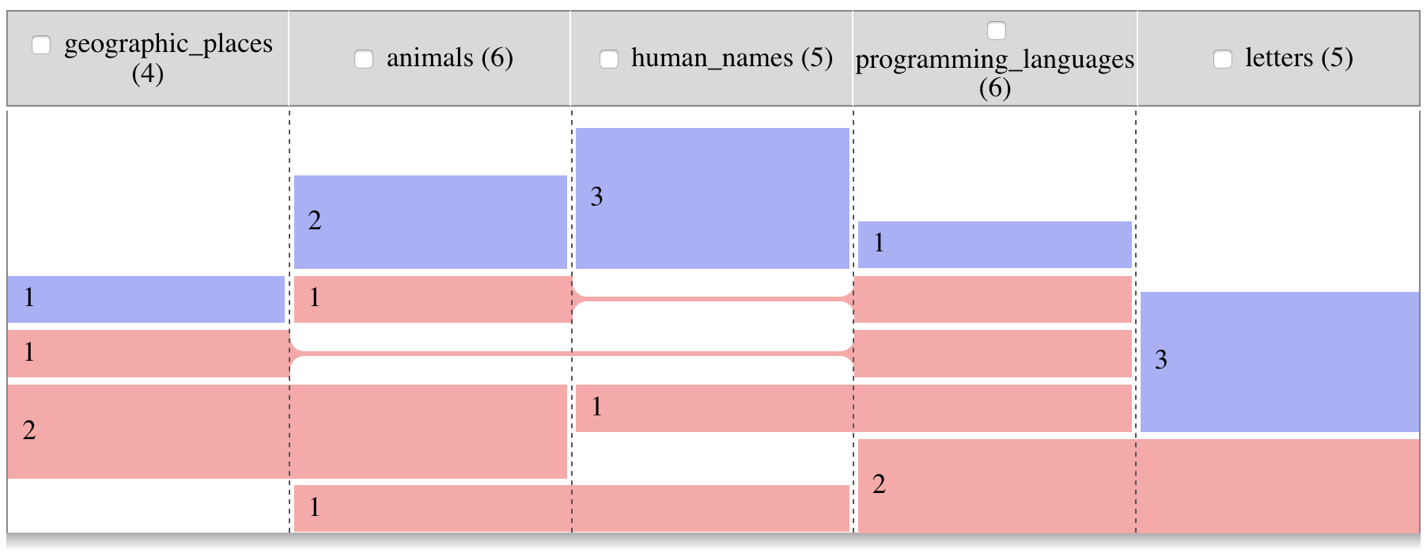
Для иллюстрации возьмём модельный пример с пятью множествами:
programming_languages = {'python', 'r', 'c', 'c++', 'java', 'julia'}
geographic_places = {'java', 'buffalo', 'turkey', 'moscow'}
letters = {'a', 'r', 'c', 'i', 'z'}
human_names = {'robin', 'julia', 'alice', 'bob', 'conrad'}
animals = {'python', 'buffalo', 'turkey', 'cat', 'dog', 'robin'}Действуя, как описано выше, получаем вот такой рисунок:
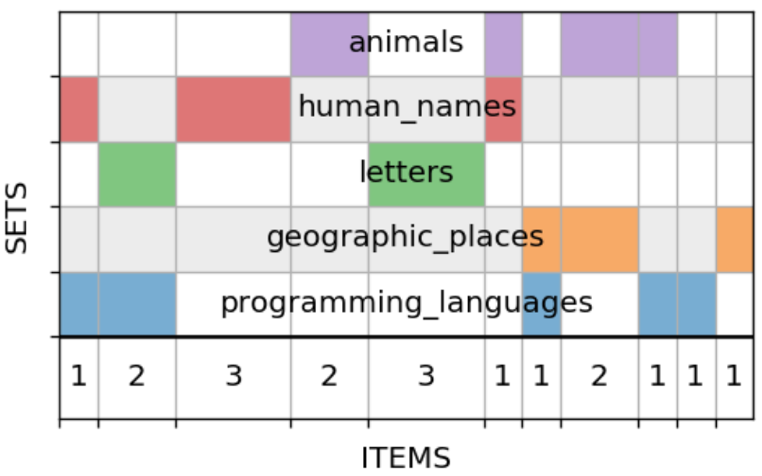
Читается он плохо: в строках слишком много разрывов, все множества порублены в капусту. Но раз нам не нравятся разрывы, то почему бы прямо не поставить задачу — минимизировать их? Ведь порядок столбцов несущественен, ничто не мешает нам переставлять их, как захочется. Приходим к такой задаче: найти перестановку столбцов данной матрицы из нулей и единиц с минимальным числом разрывов между единицами в строках.
Как мне подсказали уже позже, это практически задача коммивояжера в метрике Хэмминга, она NP-полная. Если столбцов получилось немного (скажем, не более 12), то найти нужную перестановку можно полным перебором, а иначе надо прибегать к тем или иным эвристикам.
Применим несложный жадный алгоритм. Назовём похожестью двух столбцов число позиций, на которых значения в этих столбцах совпадают. Возьмём два самых похожих столбца, поставим их вместе. Далее будем жадно наращивать последовательность в обе стороны от этой пары. Среди оставшихся столбцов найдём тот, который наиболее похож на один из этих двух, приставим — и так далее с остальными столбцами.
Вот рисунки до и после применения алгоритма:

Стало гораздо лучше. Именно на этой стадии я почувствовал, что выходит что-то полезное. Поэкспериментировав, я заметил, что алгоритм склонен залипать в локальных минимумах. Это удалось неплохо полечить с помощью простой рандомизации: немного зашумляем значения похожести столбцов, прогоняем алгоритм, повторяем 1000 раз, выбираем лучшее из 1000 решений.
Получился уже вполне рабочий инструмент, но в него можно добавить ещё немного полезной информации. Я сделал два дополнительных графика: на правом выведены размеры исходных множеств, а верхний для каждого пересечения показывает, во сколько из наших множеств оно входит. По сути, это ни что иное, как суммы нашей бинарной матрицы по строкам (справа) и по столбцам (вверху):
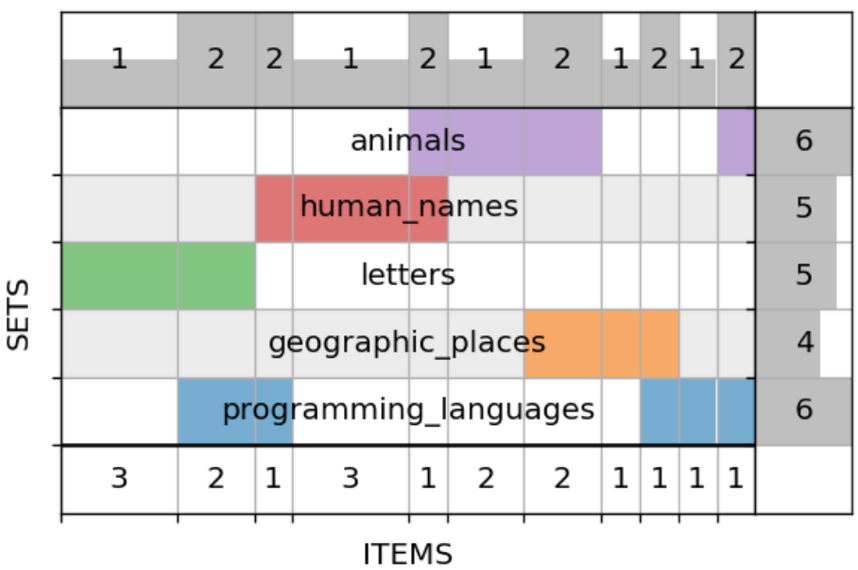
Ещё я добавил опцию упорядочивания самих множеств (т. е. строк) по тому же принципу, что и столбцов: с минимизацией числа разрывов. В итоге похожие множества группируются:
Применение в работе
Естественно, первым делом я стал применять новый инструмент для той задачи, для которой его и создавал: исследовать запросы клиентов к нашему API. Результаты меня порадовали. Вот так, например, выглядел рабочий день одного из клиентов. Каждая строка — запрос к API (множество ID входящих в него заказов), а подписи в середине — время отправки запросов:
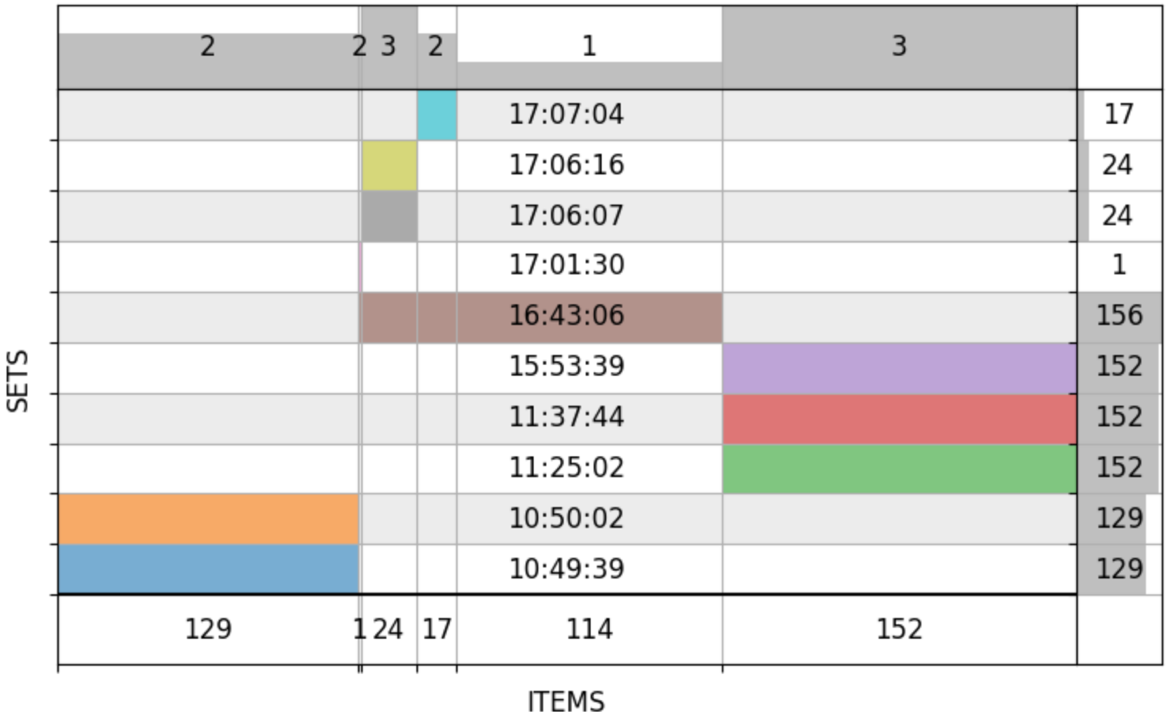
Весь день как на ладони. В 10:49 логист клиента с интервалом 23 секунды послал два одинаковых запроса со 129 заказами. С 11:25 до 15:53 было три запроса с другим набором из 152 заказов. В 16:43 пришёл третий уникальный запрос со 114 заказами. К решению этого запроса логист затем применил четыре ручные правки (это можно делать через наш UI).
А так выглядит идеальный день: все независимые задачи решены по одному разу, никаких правок или подбора параметров не потребовалось:
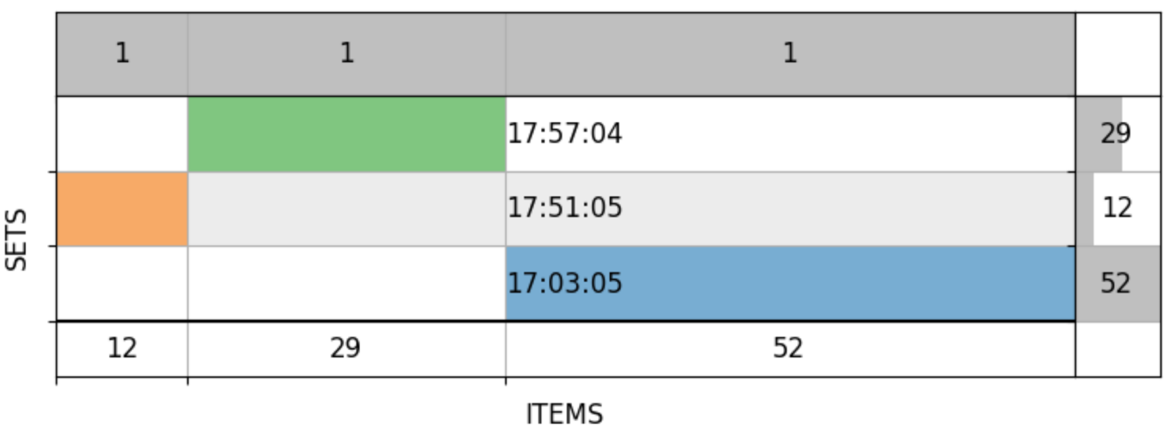
А вот пример от клиента, отправляющего запросы каждые 15–30 минут, чтобы учесть заказы, поступающие в реальном времени:
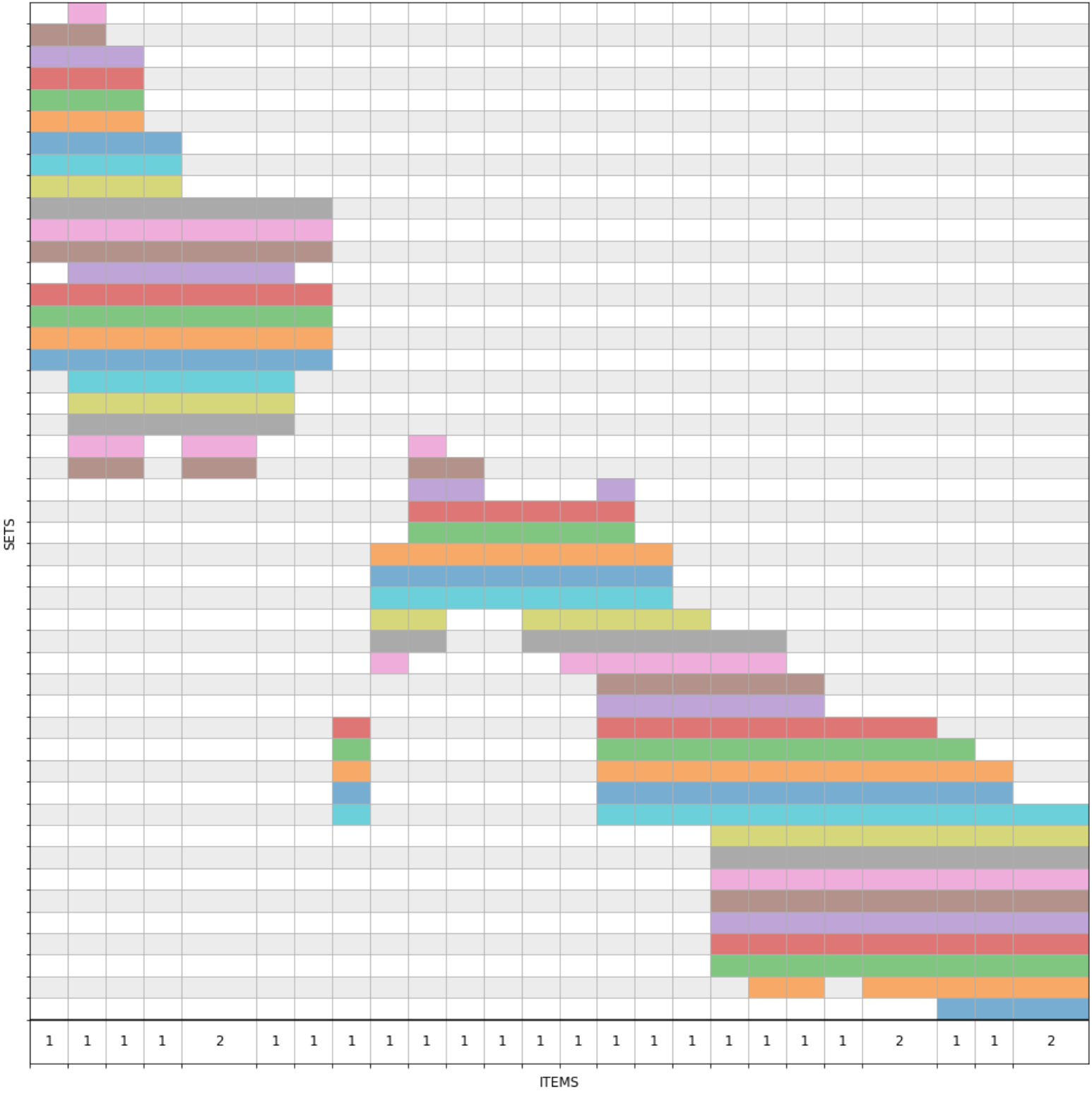
Даже на 50 множествах алгоритм хорошо выявил структуру, скрытую в данных. Видно, как старые заказы по мере исполнения убирались из запросов и замещались новыми.
Словом, закрыть созданным инструментом свою рабочую потребность мне вполне удалось.
Banana for scale (not really)
Пока я изучал существующие подходы, мне несколько раз попадался на глаза рисунок из журнала Nature, где сравниваются геномы банана и пяти других растений:
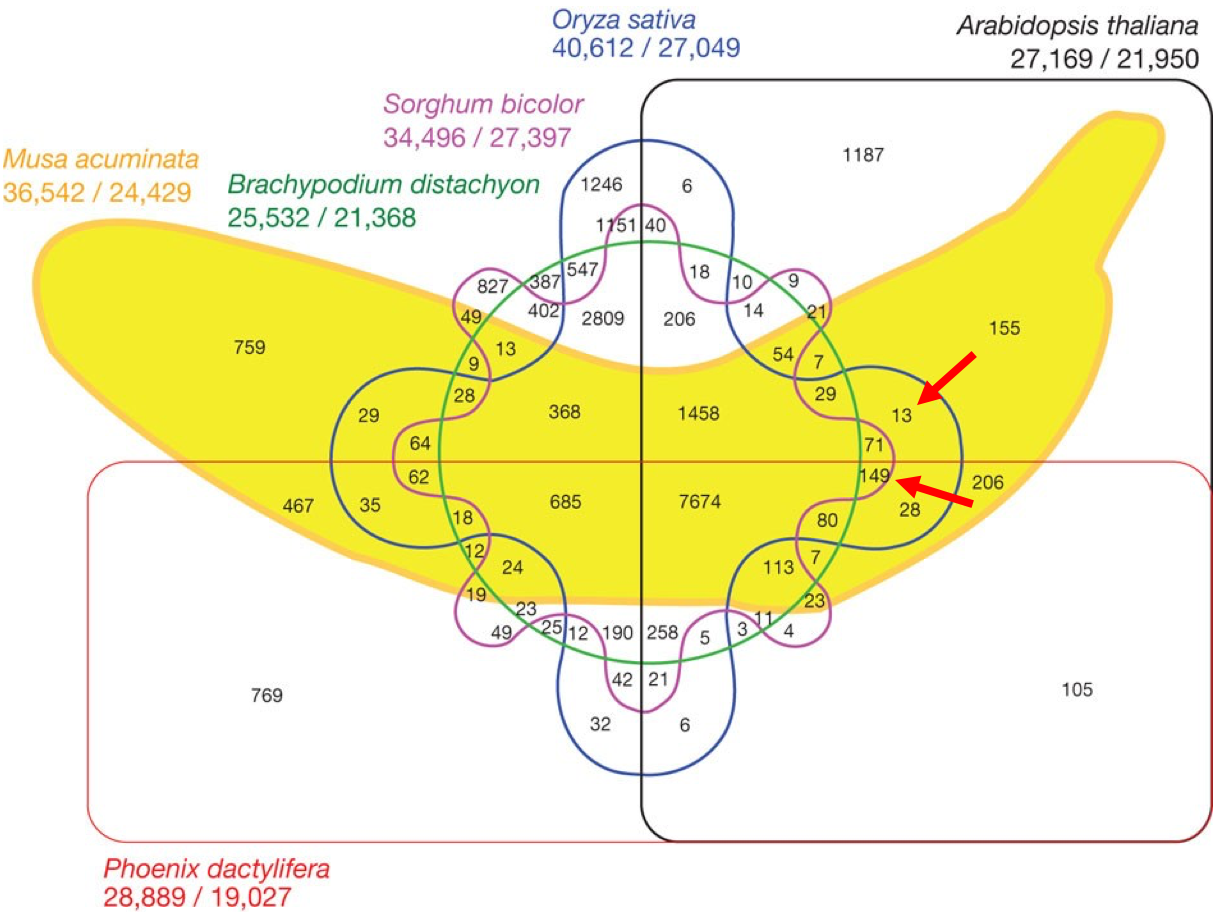
Обратите внимание, как соотносятся размеры областей с 13 и 149 элементами (указаны стрелками): вторая в несколько раз меньше. Так что ни о какой пропорциональности тут нет и речи.
Мне, конечно, захотелось попробовать силы и на таких данных, но результат меня не порадовал:

График выглядит неряшливо. Причина в том, что, во-первых, почти все пересечения (62 из 63 возможных) непусты, а во-вторых, их размеры различаются на три порядка. В результате числовым аннотациям становится очень тесно.
Чтобы мой инструмент был удобен и для таких данных, я добавил несколько параметров. Один позволяет частично выровнять ширины столбцов, другой прячет аннотации, если ширина столбца меньше заданной величины.
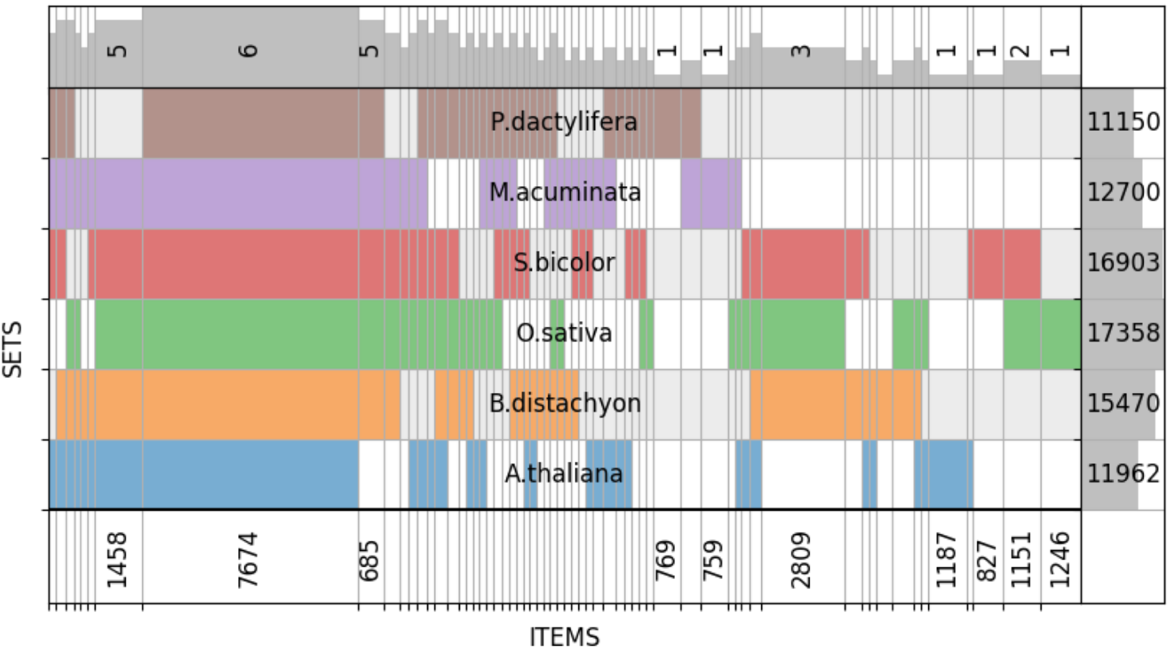
Такой вариант читается уже вполне неплохо, но ради этого пришлось пожертвовать точной пропорциональностью размеров.
Как оказалось, обратив внимание на сферу биоинформатики, я не прогадал. Я отправил пост о своём инструменте на Reddit в r/visualization, r/datascience и r/bioinformatics, именно в последнем его приняли лучше всего, отзывы были прямо-таки восторженные.
Превращение в продукт
В итоге я понял, что получился неплохой инструмент, который может быть полезен многим. Поэтому родилась идея превратить его в полноценный пакет с открытым исходным кодом. Конечно, нужно было согласие руководителей, но ребята не только не возражали, но и поддержали меня, за что им большое спасибо.
Работая в основном по выходным, я начал понемногу приводить код в товарный вид, писать тесты и разбираться с системой пакетов в Python. Это мой первый проект такого рода, поэтому всё заняло несколько месяцев.
Придумать хорошее название тоже оказалось непростой задачей, и справился я с ней плоховато. Выбранное имя (supervenn) нельзя назвать удачным, ведь вся соль диаграмм Венна в их статичности, я же, напротив, стремился точно показывать реальные размеры. Но когда я это осознал, проект уже вышел в свет и менять название было поздно.
Аналоги
Конечно, я не первый использовал этот подход к визуализации множеств: идея, в общем-то, лежит на поверхности. В открытом доступе есть два похожих веб-приложения: RainBio и Linear Diagram Generator, второе использует в точности тот же принцип, что и у меня. (Авторы вдобавок написали статью на 40 страниц, где экспериментально сравнили, что лучше воспринимается — горизонтальные или вертикальные линии, тонкие или толстые и т. п. Мне даже показалось, что для них первичной была именно статья, а сам инструмент — лишь дополнение к ней.)
Чтобы сравнить эти два приложения с моим пакетом, снова используем пример со словами. Можете сами решить, какой вариант более удобочитаем и информативен.
RainBio
Linear Diagram Generator

supervenn

Другие подходы
Нельзя не упомянуть проект UpSet, существующий в виде веб-приложения и пакетов для R и Python. Базовый принцип можно понять, посмотрев на отображение данных о геноме банана. График обрезан справа, показаны только 30 пересечений из 62:
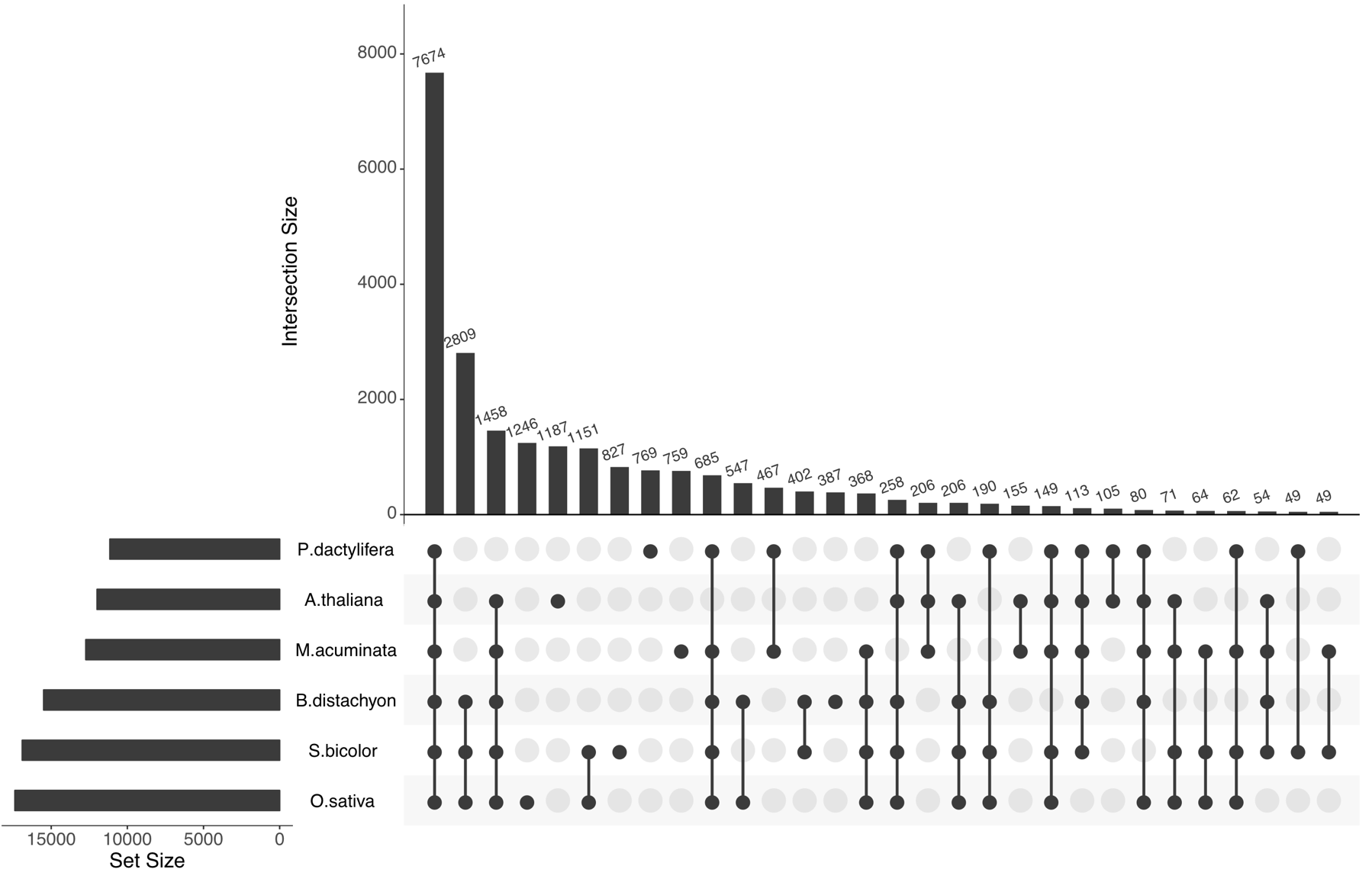
Интересно, что если использовать supervenn с сортировкой столбцов по ширине и сделать столбцы одинаковыми с помощью параметра выравнивания ширин, то получится почти то же самое, хотя это и не сразу заметно. Не хватает лишь вертикальных линий с размерами пересечений, вместо них только цифры внизу графика:
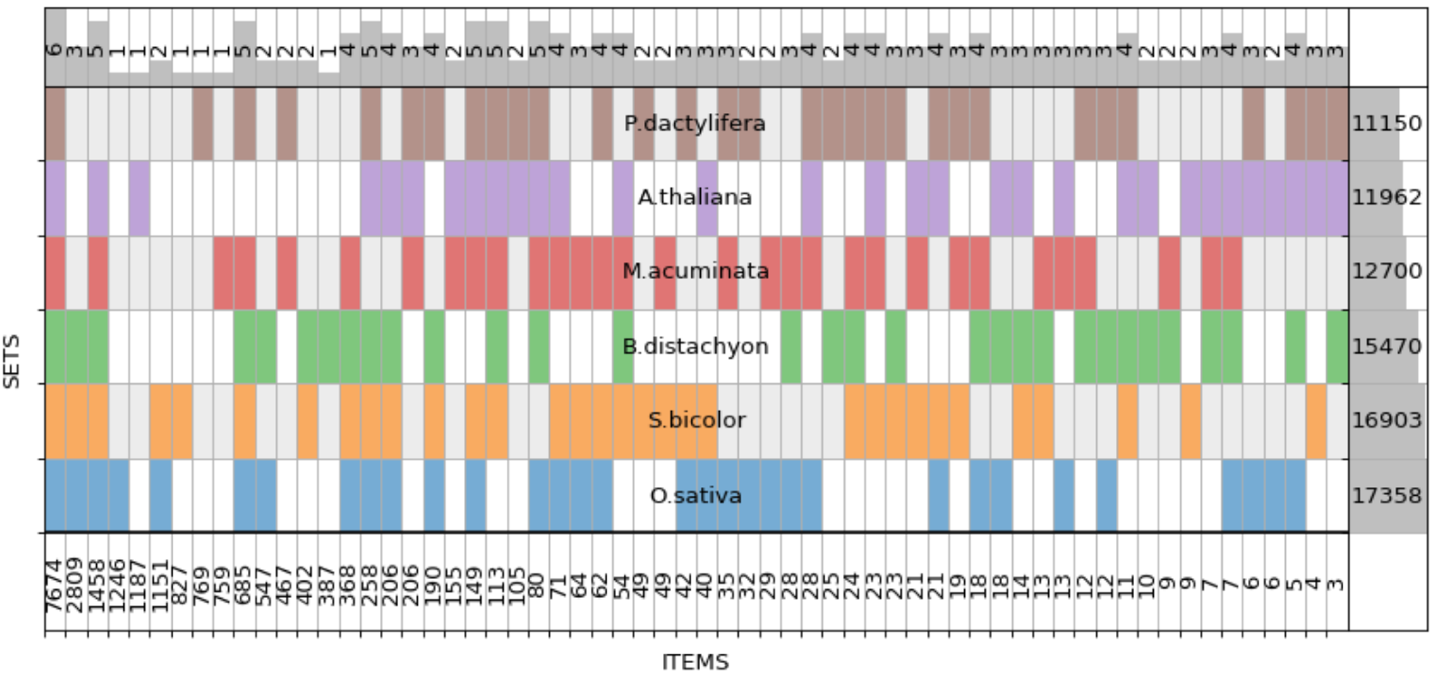
Уже при написании этого текста я попробовал воспользоваться Python-версией UpSet, но обнаружил, что пакет не обновлялся с 2016 года, в документации никак не описан формат входных данных, а тестовый пример падает с ошибкой. Веб-версия исправна, в ней много полезных вспомогательных функций, но работать с ней довольно тяжело из-за сложного способа ввода данных.
Наконец, в сети доступен интересный обзор методов визуализации множеств. Далеко не все из них реализованы в виде программных инструментов. Вот несколько картинок для привлечения внимания:
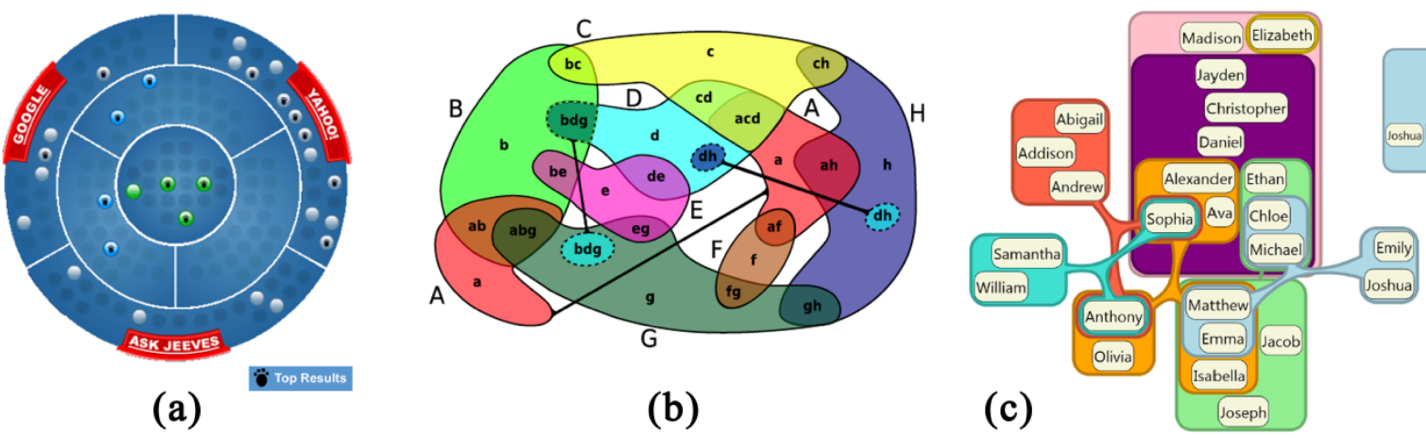
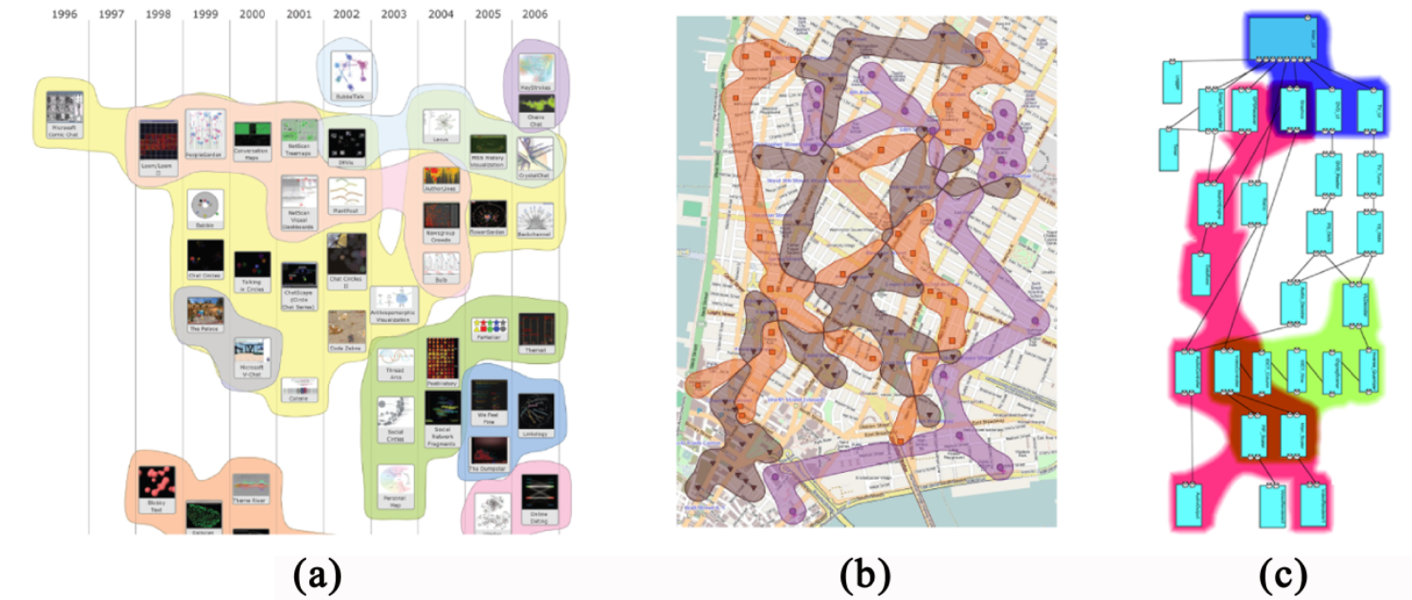
Особенно меня заинтересовал метод Bubble Sets (нижний ряд), позволяющий изображать небольшие множества поверх заданного расположения элементов на плоскости. Это может быть удобно, например, когда элементы привязаны к оси времени (а) или к карте (b). Пока что этот метод реализован только на Java и JavaScript (ссылки есть на странице авторов), и было бы здорово, если бы кто-нибудь взялся портировать его на Python.
Я отправил письма с кратким описанием проекта авторам UpSet и обзора и получил хорошие отзывы. Двое из них даже обещали включить supervenn в свои лекции по визуализации множеств.
Заключение
Если вы захотите воспользоваться пакетом, он доступен на GitHub и в PyPI: pip install supervenn. Я буду благодарен за любые замечания о коде и использовании пакета, за идеи и критику. Особенно буду рад прочитать рекомендации, как улучшить алгоритм перестановки столбцов для больших
Спасибо за внимание!
Ссылки
1. John Venn. On the diagrammatic and mechanical representation of propositions and reasonings. The London, Edinburgh and Dublin Philosophical Magazine, July 1880.
2. J.-B. Lamy and R. Tsopra. RainBio: Proportional visualization of large sets in biology. IEEE Transactions on Visualization and Computer Graphics, doi: 10.1109/TVCG.2019.2921544.
3. Peter Rodgers, Gem Stapleton and Peter Chapman. Visualizing Sets with Linear Diagrams. ACM Transactions on Computer Human Interaction 22(6) pp. 27:1-27:39 September 2015. doi:10.1145/2810012.
4. Alexander Lex, Nils Gehlenborg, Hendrik Strobelt, Romain Vuillemot, Hanspeter Pfister
UpSet: Visualization of Intersecting Sets. IEEE Transactions on Visualization and Computer Graphics (InfoVis’14), 2014.
5. Bilal Alsallakh, Luana Micallef, Wolfgang Aigner, Helwig Hauser, Silvia Miksch and Peter Rodgers. The State-of-the-Art of Set Visualization. Computer Graphics Forum. Volume 00 (2015), number 0 pp. 1–27 10.1111/cgf.12722.
6. Christopher Collins, Gerald Penn and Sheelagh Carpendale. Bubble Sets: Revealing Set Relations with Isocontours over Existing Visualizations. IEEE Trans. on Visualization and Computer Graphics (Proc. of the IEEE Conf. on Information Visualization), vol. 15, iss. 6, pp. 1009−1016, 2009.
