Введение
В данном топике я хочу рассказать о модели необычной нейронной сети, в разработке которой мне посчастливилось участвовать. Данная модель была разработана около года назад (про авторство написано в последнем разделе), однако исследование ее после этого прекратились из-за совершенной нехватки времени (занятости в своих собственных проектах). Тем не менее я опишу ее здесь в надежде на то, что некоторые мысли покажутся читателям интересными и дадут ростки возможных дальнейших исследований в данном направлении.
Сразу оговорюсь, что эта модель не претендует никоим образом на прототип ИИ. Мы скорее хотели исследовать возможность самоорганизации и перспективы возникновения целостного целенаправленного поведения в динамической системе «эгоистичных» (гомеостатических) нейронов.
Как мне кажется, для более полного понимания логики работы модели будет полезно прочитать мой топик про Теорию функциональных систем, однако опять же это на ваше усмотрение.
Поехали!
Биологическое основание
Данная модель строилось на основании теории функциональных систем П.К. Анохина и теории гомеостаза.
Гомеостаз — саморегуляция, способность открытой системы сохранять постоянство своего внутреннего состояния посредством скоординированных реакций, направленных на поддержание динамического равновесия. Уолтер Кэнон, который изначально ввел этот термин, называл гомеостаз «мудростью тела» [1].
Простейшие биологические мотивации возникают при нарушении гомеостатического равновесия в нейронах соответствующих физиологических зон (нарушение запасов энергии, кислорода или осмотический дисбаланс). Тем не менее, существует некая универсальная единица для оценки биологической мотивации [2]. Существование этой единицы связано с тем, что удовлетворение любой мотивации вызывает удовольствие и, соответственно, удаление дисбаланса в гомеостатической системе, который и порождает данную мотивацию. Поэтому моделирование гомеостаза – это прямой путь к созданию искусственной системы, обладающей некоторым подобием мотивации, т.е. системы, имеющую собственную цель и пути к ее достижению. Есть множество факторов, ведущих к рассогласованию в системе гомеостаза, причем наблюдается иерархия таких факторов, по степени их важности для выживания клетки. Для сохранения факторов высшего уровня в стабильном диапазоне гомеостаз изменяет оптимальные уровни регулирования факторов нижнего уровня. Т.е. восстановление функции может происходить не через возвращение искаженных параметров к норме, а обходным путем, через изменения соотношения между этими параметрами. В частности, избыточное возбуждение повреждает нейроны, но есть некоторые факторы, восстанавливающие гомеостаз (как цАМФ, Интерлейкин-1, тиротропин-выделяющий гормон). Следовательно, компенсационный гомеостаз может на промежуточном этапе возбуждать нейроны на пути к поиску новой точки равновесия. На рис. 1. изображена схема двухуровневого гомеостаза в нейроне. Красным цветом на рисунке условно показано повреждение нейрона, а зеленым – восстановление. Повреждение – это внешний фактор, порождающий рассогласование.
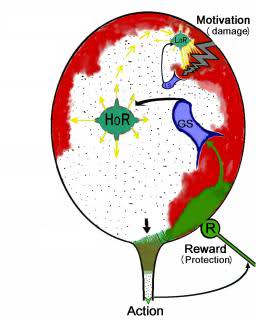
Рис. 1. Гомеостаз нейрона
(LoR – гомеостаз низкого уровня, HoR – гомеостаз высокого уровня, LS – локальный сенсор рассогласования, R – награда снижающая уровень рассогласования)
В литературе известен набор моделей гомеостаза [3,4], но они не ориентированы на самоорганизацию нейронных сетей и целенаправленное поведение. Моделирование целенаправленного поведения, в том числе на основе нейронных сетей и обучения с подкреплением, также имеет богатую историю и широко освещена в литературе. Однако в рамках этих моделей не рассматривался гомеостаз нейронов и сетей в целом.
Собственно, исходя из всего вышесказанного, была сформулировано иерархия моделей, которые составят полную систему:
— модель гомеостатического нейрона, объединяющая ключевые характеристики известных моделей и основные принципы рассматриваемой парадигмы;
— модели гомеостатической нейронной сети, основанной на гомеостатических нейронах;
— модель простейшего организма, управляемого гомеостатической нейронной сетью, и его взаимодействия со средой;
— моделирование эволюционного развития простейших организмов в условиях изменяющейся внешней среды.
Модель гомеостатического нейрона и нейронной сети
Так как основной задачей является анализ парадигмы гомеостатического нейрона как возможной основы механизма самоорганизации нейронной сети и ее способности к автономному поведению, то особенное внимание необходимо уделить именно этой ключевой первичной модели. Модель гомеостатического нейрона подразумевает, что каждый нейрон стремится к поддержанию своего оптимального внутреннего состояния – гомеостаза, причем при рассогласовании текущего состояния с оптимальным, нейрон формирует ответ, направленный на возвращение к оптимальному состоянию. Как уже упоминалось ранее изменение множества факторов может привести к нарушению равновесия нейрона, однако в модельной ситуации введем некоторую единую эндогенную оценку состояния нейрона q(t), имеющую предопределённое оптимальное значение qopt. Также введем показатель величины внутренней энергии e(t), отражающий возможности нейрона по генерации сигналов x(t) и поддержанию гомеостаза собственной активности.
Стремление нейрона к гомеостазу выражается в активности, направленной на устранение рассогласования qopt-q(t), тем более выраженной, чем больше величина рассогласования. Активность нейрона требует энергетических затрат, поэтому может принимать разные формы в зависимости от количества имеющейся энергии e(t).
Таким образом, мы сформулировали некоторые требования к модели «эгоистического» нейрона, т.е. такого нейрона который имеет одну цель – поддерживать свое состояние близкое к оптимальному. Однако, каждый нейрон не может существовать изолировано, а обязан функционировать в целостной нейронной сети. Таким образом, мы можем ввести понятие вектора воздействия на конкретный нейрон со стороны остальной сети:

Это воздействие меняет эндогенную оценку нейрона на следующий такт времени:
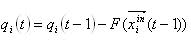
Данная функция может выглядеть по разному, однако самый просто ее случай – это

Получается, что выше мы ввели все характеристики нейрона, а также методику определения воздейтсвия на нейрон со стороны остальных нейронов. Теперь мы введем понятие рассогласования нейрона g(t), смысл которого мы уже касались выше, а также собственно понятие действия нейрона и выходного сигнала. Рассогласование нейрона:

Теперь определим действие нейрона, которое он выбирает на основе текущего рассогласования:

На этом этапе необходимо остановится подробнее, так как с одной стороны он является одним из ключевых во всей модели, а с другой стороны само понятие действия аккумулирует в себе несколько биологических принципов и наших размышлений, о которых было сказано выше.
Первое, что необходимо заметить – это то, что любое воздействие на нейрон со стороны других нейронов влечет к отклонению от его гомеостатического равновесию. Соответственно все действия нашего «эгоистичного» нейрона должны быть направлены на возвращение к этому равновесию. В этом заключается принцип гомеостаза низкого уровня. Тут возможны несколько случаев, которые собственно и были рассмотрены при составлении функции действия.
Действие нейрона в первую очередь зависит от степени его рассогласованности. Если нейрон находится далеко от точки гомеостатического равновесия, то он осуществляет действие, которое немедленно возвращает его к равновесию – генерацию спайка. Если же он близок к равновесию, то включается другой механизм гомеостаза – медленное восстановление. На каждое действие нейрон тратит энергию: на спайк – большую, а на восстановление – не очень большую. Про пополнение энергии нейрона будет рассказано далее.
Кроме этого энергии нейрона может не хватить на генерацию спайка, даже когда он необходим, что означает выбор восстановление до того момента, пока энергия не пополнится.
Таким образом, действие нейрона является функцией от входного сигнала, эндогенной оценки состояния и запаса энергии. Собственно на этом заканчивается формальная модель нейрона (в том числе гомеостаза нижнего уровня) и сети в целом. На рис. 2 приведено схематическое изображение «эгоистического» нейрона.

Рис. 2. «Эгоистичный» нейрон
Модель организма
Нейронная сеть является частью целого организма, однако для его полного определения необходимо ввести еще несколько дополнительных понятий. Первое из них – это общий пул энергии Е(t), из которого восстанавливаются энергии всех нейронов сети. Если e(t)<emin (оптимальный запас энергии нейрона), то
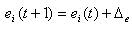
Теперь нам необходимо определить понятие гомеостаза высшего уровня.
Введем понятие эндогенной оценки состояния всей сети:
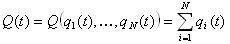
При это будем считать, что есть некоторое оптимальное состояние Qopt:
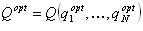
Тогда определимся, что гомеостаз высшего уровня вступает в действие в двух различных случаях:
— после установления стабильности (в случае если в сети наблюдается циклический процесс, но состояние не достигает оптимального значения)
— при «возникновении потребности» (в случае большого рассогласования эндогенной оценки состояния сети)
В этом случае происходит изменение параметров qiopt случайным образом, при этом величина изменения каждого значения пропорциональна, как рассогласованию эндогенной оценки состояния сети, так и рассогласованию эндогенной оценки конкретного нейрона. Таким образом, при невозможности системы достичь оптимального состояния и при угрозе жизни всей сети, включается механизм гомеостаза высшего уровня. Cхематично такая модель организма показана на рис. 3.
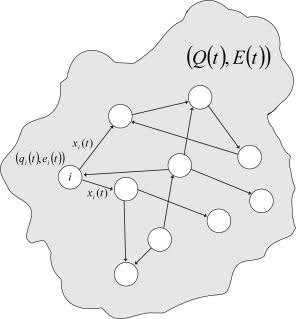
Рис. 3. Модель организма
Здесь, наверное необходимо привести некоторые экспериментальные данные, по которым можно будет судить о качественной динамики такой модели (без гомеостаза высшего уровня). Мы составили сеть из 10 нейронов со случайно распределенными весами по распределению Wij~N(0,1) и с различными оптимальными значениями эндогенной оценки состояния и запаса энергии. При этом на момент инициализации 9 нейронов находились в состоянии равновесия, а один из нейронов был рассогласован. На рис. 4-5 приведены зависимости от времени эндогенной оценки состояния и энергии каждого нейрона в такой системе.

Рис. 4. График динамики эндогенной оценки состояния нейронов
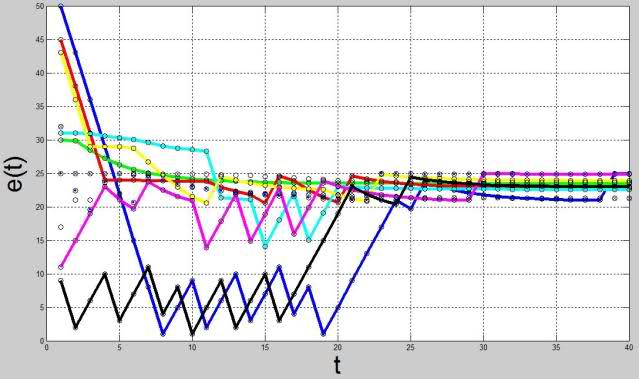
Рис. 5. График динамики запаса энергии нейронов
По рисункам видно, что в итоге вся система приходит в положение гомеостатического равновесия, однако наши опыты показывают, что существует область параметров, при которых достижение гомеостатического равновесия невозможно и в системе начинается автоколебательный процесс, что свидетельствует о необходимости включения гомеостаза высшего уровня.
Взаимодействие со средой
Представим себе, что мы помещаем такой организм в среду. Предположим, что у нашего организма всего одна потребность – потребность в поддержании достаточного уровня общей энергии, которая расходуется на гомеостаз и на метаболические процессы. В таком случае необходимо, чтобы организм мог принимать решение в нужный момент о восполнении уровня энергии. То есть, например нажимать на кнопку, чтобы ему подавалась еда.
Мы думали о введение макропараметров организма, изменение которых определяет его потребности (их может быть несколько), а также о рассмотрение набора эффекторов, позволяющих организму изменять значения своих макропараметров за счет взаимодействия с внешней средой. В основе предлагаемого подхода к проблеме лежит передача информации о значениях макропараметров непосредственно гомеостатическим нейронам, что связывает внутренний гомеостаз нейрона с удовлетворением соответствующей потребности. Таким образом, гомеостаз второго уровня отвечает за работоспособность системы в целом, а первого уровня – за эффективную линию поведения организма при взаимодействии с окружающей средой.
Поясню на примере. Для этого предположим, что в структуре нейронной сети присутствует два специализированных нейрона.
Первый нейрон специализирован относительно потребности в восполнении энергии, то есть он вступает в рассогласование в случае, если уровень общей энергии недостаточен. То есть у него есть дополнительный вход, на который поступает уровень недостатка общей энергии ( E-Emin). Второй нейрон специализирован относительно выполнения действия восполнения энергии, то есть в тот момент, когда он генерирует спайк происходит восполнение общей энергии из внешней среды. Данная система изображена на рис. 6.
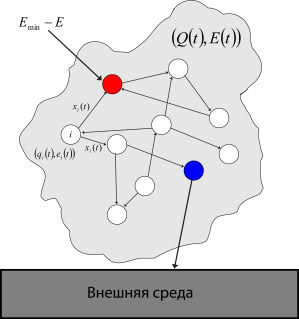
Рис. 6. Взаимодействие организма со средой
красный нейрон специализирован относительно потребности в восполнении энергии, синий — относительно выполнения действия восполнения энергии)
Таким образом, рассогласование в организм вносится в тот момент, когда он испытывает потребность в еде. В свою очередь нейроны пытаются устранить это рассогласование. Пока не будет наблюдаться спайк на нейроне специализированном относительно выполнения действия, восполнение энергии не произойдет, и сигнал о недостатке энергии будет продолжать поступать в систему. Таким образом, в какой-то момент спайк генерируется на втором специализированном нейроне и запас общей энергии пополняется, из-за чего нейрон, который специализирован относительно потребности в восполнении энергии перестает быть рассогласованным.
Безусловно это очень модельная ситуация, однако она показывает по какой логике может функционировать такой организм в среде, где требуется принимать некоторые решения.
Непрерывная модель
Исключительно для тех, кто задумается о том, как можно эту дискретную во времени модель сделать непрерывной, привожу наш вариант, основанный на модели нейронов ФитцХью-Нагумо.
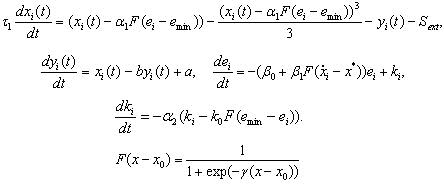
Заключение
Безусловно данная модель не может претендовать на хоть какую-то законченность. Однако, мне кажется, что некоторые мысли в нее заложенные, достаточно интересны и могут стать объектом исследования читателей. В частности идея рассогласования нейрона, как мотивации для совершения действия, определение рассогласования – как соотношения внутренних параметров нейрона с микросредой, а также гомеостаз – как основа для устранения рассогласования и для самоорганизуещего эффекта.
Также этим топиком я хотел обратить внимание читателей на то, что даже в достаточно простых моделях могут возникать интересные эффекты самоорганизации, которые в перспективе могут приводит к целостному поведению.
Отмечу, что в данном обзоре я не касался нетривиального вопроса введения процесса обучения в эту модель, а также собственно эволюции. Все это остается предметом дальнейших возможных исследований.
Авторство
В разработке данной модели принимали участие Максим Комаров (Нижегородский университет), Даниил Каневский (ВМиК МГУ), Сергей Куливец (ИПУ РАН), а также ваш покорный слуга. Также огромной благодарности заслуживают Лев Ефимович Цитоловский (Бар-Иланский Университет, Израиль) и Владимир Георгиевич Редько (НИИСИ РАН) за их поддержку и слежение за направлением наших мыслей, когда нас заносило. Каждый из нас привнес в эту модель свои мысли и соображения из областей, которыми мы занимаемся.
Список литературы
[1]. Cannon W. B. Physical Review, 1928, 9:399-431.
[2]. Cabanac M. Journal of Theoretical Biology, 1992, 155:173-200.
[3]. Davis G.W. Annual Review of Neuroscience, 29:307-323, 2006.
[4]. Marder A., Prinz A. A. BioEssays, 24: 1145-1154, 2002






