На данный момент происходит лавинообразное увеличение числа мультимедиа-ресурсов, в частности изображений. Как следствие, возрастают требования к средствам систематизации и поиска подобных ресурсов. Большинство существующих на данный момент систем,
осуществляющих поиск информации по описанию (англ. Description-Based Image Retrieval, DBIR), уже не могут в полной мере удовлетворить потребности человека. Поэтому все больше растет интерес к поиску объектов по содержанию (англ. Content-Based Image Retrieval, CBIR).
Следует отметить, что во многих сферах деятельности пользователю приходится сталкиваться с изображениями человеческих лиц: начиная от стремительно развивающихся социальных сетей и заканчивая областью криминалистики. И хотя к данной задачи применимы общие методы поиска и классификации, она требует более высокой точности решения. Подобное требование объясняется, по большему счету, сложностью строения самого лица и множеством деталей, затрудняющих выделить общие типы лиц (родинки, прически, растительность на лице и т.д.). Вполне естественно, что требование к точности результата ведет к повышению вычислительных затрат алгоритмов поиска и распознавания лиц.
Существует довольно большое число методов, позволяющих обрабатывать изображения лиц: метод собственных лиц, нейросети и т.д. Среди них можно выделить алгоритмы, основанные на скрытых марковских моделях. Данный метод показывает одни из самых высоких результатов в задачах распознавания лиц.
Прежде чем перейти к рассмотрению моделей, рассмотрим, что представляет собой марковская цепь (марковский процесс). Последовательность случайных переменных Xn называется марковской цепью, если:
P(Xn= a | Xn-1 = b, Xn-2 = c, …, X0 = x) = P (Xn | X = b).
Доказано, что марковские цепи позволяют создавать довольно простые и информативные картины. Можно, например, изобразить взвешенный направленный граф с узлом для каждого состояния и весовым коэффициентом на каждом ребре, указывающем вероятность перехода между состояниями:
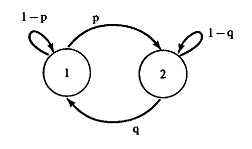
При наблюдении случайной переменной Xn известно, в каком состоянии находится цепь. Эта модель, к сожалению, слишком ограничена и ей не под силу решение многих актуальных проблем. Более совершенную модель можно получить, положив, что для каждого элемента последовательности наблюдается иная случайная переменная, распределение вероятностей которой зависит от состояния цепи – наблюдается некоторая переменная Yn, причем распределение вероятностей в некоторой точке P(Yn| Xn= si) = qi (Yn). Данные элементы можно собрать в матрицу Q. Модели подобного рода называются скрытыми марковскими моделями (СММ). Для задания СММ требуется обеспечить процесс перехода между состояниями, связи между состоянием и распределением вероятности
Yn, а также знать исходное распределение состояний.
Рассмотрим формальное описание скрытой марковской модели. Каждая модель определяется следующими параметрами:
Каждый элемент вложенной СММ называется суперсостояниеми представляет собой отдельную одномерную марковскую модель с параметрами, описанными выше.
Цифровое изображение – суть случайный двумерный дискретный сигнал, наблюдаемый системой. Последовательность наблюдений (вектор наблюдений) может извлекаться из изображения различными способами. В силу этого описательные способности полученных моделей могут различаться. Наиболее предпочтительным является вариант сканирования изображения прямоугольным окном. Для уменьшения вероятности потери данных на границах блоков, рекомендуется сканировать изображение таким образом, что соседние блоки пикселей могут перекрываться друг другом. Значение перекрытия подбирается экспериментально.
Для снижения вычислительной сложности и уменьшения пространства признаков, каждый извлеченный блок пикселей подвергается некоторому преобразованию, в результате которого получается некоторый набор числовых данных, который и является вектором наблюдений.
Наиболее подходящими для поставленной задачи являются два преобразования:
Далее, полученные вектора распределяются по состояниям модели. Здесь необходимо отметить, что каждая отдельная СММ представляет некоторый класс объектов. Тогда состояния модели определяют некоторые ключевые признаки класса. К примеру, СММ для поиска лиц состоит из 5 суперсостояний, соответствующих областям лица (лобовая часть, глаза, нос, рот, подбородок), каждое из которых делится на отдельные состояния.
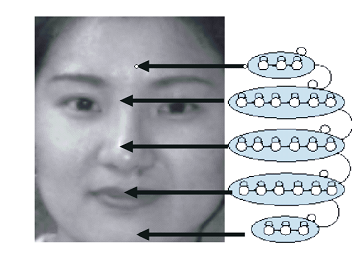
Переход в следующее состояние возможно только после предыдущего, а переход в следующее суперсостояние возможно только после всех состояний текущего суперсостояния. Вероятность принадлежности некоторого объекта заданному классу, оценивается как вероятность генерации сигнала, соответствующего его вектору признаков.
Предполагаем, что информация об изображениях коллекции хранится в какой-либо реляционной базе данных. Содержание изображений может быть определено на различных уровнях абстракции. На низшем уровне изображение представляет собой набор пикселей. Уровень пикселей редко используется в задаче поиска, так как это предполагает больших вычислительных и временных затрат.
Необработанные данные могут быть отправлены для генерации числовых дескрипторов, описывающих особенные визуальные характеристики, называемые сигнатурами. Как правило, уровень сигнатур изображения требует гораздо меньшего пространства, чем изображение.
Поиск изображений основан на поиске схожести в многомерном пространстве. При этом изображение определяется набором своих сигнатур. Мера схожести – это функция, которая вычисляет и возвращает значение, соответствующее схожести между двумя объектами согласно некоторым предопределенным критериям. Понятие меры сходства основывается на понятии метрики. Метрика – это функция расстояния d, определенная на метрическом множестве, для любых точек x, y, z которого
выполняются условия:
1. ,
,
2.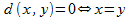 ,
,
3. .
.
Индексирование и поиск изображений в коллекциях производится на основе треугольного дерева (triangle tree, trie дерево), также называемое Really Fixed Query Tree. Треугольное дерево – это структура данных, разработанная для поиска приблизительных совпадений в зависимости от усилий поиска. Оно ассоциируется с мерой расстояния, набором ключевых изображений и набором элементов базы данных. Форма trie – это форма дерева, в котором ребра следуют от корня до листьев, определяя индекс листа. Листья дерева содержат элементы базы. Каждое внутреннее ребро в дереве ассоциируется с неотрицательным числом. Каждый уровень дерева ассоциируется с одиночным ключом. Путь от корня до листьев представляет собой расстояние от элемента базы данных до каждого из ключей.
На рисунке представлено треугольное дерево с 4 элементами (W, X, Y, Z) и 2 ключа (J, K). Расстояние от листа W до ключа J равно 3, расстояние от W до K равно 1. Таким образом, каждое изображение будет характеризоваться некоторым набором числовых значений, определенных как расстояния от этого изображения до существующих ключей.
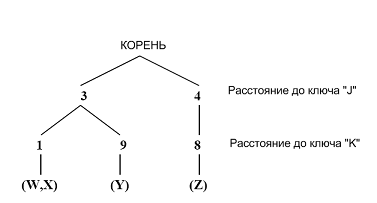
Процесс индексирования изображений коллекции заключается в поиске расстояний от каждого изображения до каждого ключа. Исходя из вышесказанного, можно определить принцип поиска следующим образом. Пусть I представляет объект базы, Q представляет объект запроса, K представляет ключевые изображения и d определяет некоторые меры сходства – метрики. Используя свойство метрики (3), заключаем, что следующие неравенства будут верными:

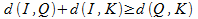
Комбинируя неравенства, получаем выражение, определяющее расстояние от объекта запроса до объекта коллекции:
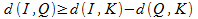
Таким образом, сравнивая объекты из базы данных и объекты запроса с третьим ключевым объектом, может быть получена нижняя граница дистанции между двумя объектами. На основе этой границы можно отсечь большую часть коллекции, как не удовлетворяющую запросу.
Также необходимо отметить, что процесс поиска происходит в два этапа. На первом этапе определяется нижняя граница расстояния от изображения запроса до изображений коллекции. На этой стадии происходит отсечение части коллекции. На втором этапе происходит уточняющий поиск: определяется расстояния от изображения-запроса до каждого изображения, из найденных на первой стадии. Изображения, соответствующие максимальным расстояниям, составляют итоговый результат поиска.
На основе вышесказанного можно сделать вывод, что для того, чтобы воспользоваться поиском и индексацией, для каждого изображения необходимо уметь производить следующие действия.
Вторая проблема заключается в том, что на данном этапе не представляется возможным использовать СММ для поиска расстояния между двумя отдельными изображениями. Это объясняется тем, что алгоритмы поиска требуют обученной модели: обучение модели на одном изображении является проблематичным.
При подготовке статьи использовались следующие материалы:
осуществляющих поиск информации по описанию (англ. Description-Based Image Retrieval, DBIR), уже не могут в полной мере удовлетворить потребности человека. Поэтому все больше растет интерес к поиску объектов по содержанию (англ. Content-Based Image Retrieval, CBIR).
Следует отметить, что во многих сферах деятельности пользователю приходится сталкиваться с изображениями человеческих лиц: начиная от стремительно развивающихся социальных сетей и заканчивая областью криминалистики. И хотя к данной задачи применимы общие методы поиска и классификации, она требует более высокой точности решения. Подобное требование объясняется, по большему счету, сложностью строения самого лица и множеством деталей, затрудняющих выделить общие типы лиц (родинки, прически, растительность на лице и т.д.). Вполне естественно, что требование к точности результата ведет к повышению вычислительных затрат алгоритмов поиска и распознавания лиц.
Существует довольно большое число методов, позволяющих обрабатывать изображения лиц: метод собственных лиц, нейросети и т.д. Среди них можно выделить алгоритмы, основанные на скрытых марковских моделях. Данный метод показывает одни из самых высоких результатов в задачах распознавания лиц.
Скрытые марковские модели
Прежде чем перейти к рассмотрению моделей, рассмотрим, что представляет собой марковская цепь (марковский процесс). Последовательность случайных переменных Xn называется марковской цепью, если:
P(Xn= a | Xn-1 = b, Xn-2 = c, …, X0 = x) = P (Xn | X = b).
Доказано, что марковские цепи позволяют создавать довольно простые и информативные картины. Можно, например, изобразить взвешенный направленный граф с узлом для каждого состояния и весовым коэффициентом на каждом ребре, указывающем вероятность перехода между состояниями:
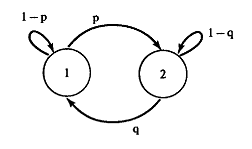
При наблюдении случайной переменной Xn известно, в каком состоянии находится цепь. Эта модель, к сожалению, слишком ограничена и ей не под силу решение многих актуальных проблем. Более совершенную модель можно получить, положив, что для каждого элемента последовательности наблюдается иная случайная переменная, распределение вероятностей которой зависит от состояния цепи – наблюдается некоторая переменная Yn, причем распределение вероятностей в некоторой точке P(Yn| Xn= si) = qi (Yn). Данные элементы можно собрать в матрицу Q. Модели подобного рода называются скрытыми марковскими моделями (СММ). Для задания СММ требуется обеспечить процесс перехода между состояниями, связи между состоянием и распределением вероятности
Yn, а также знать исходное распределение состояний.
Рассмотрим формальное описание скрытой марковской модели. Каждая модель определяется следующими параметрами:
- Множество S = {s1, s2, …, sN} из N состояний.
- Начальное распределение вероятностей P = {pi}.
- Матрица вероятностей переходов между состояниями A = {ai}.
- Матрица вероятности генерации наблюдений B = {bj(Ot)}, где bj(Ot) – вероятность генерации наблюдения Ot в момент времени t в состоянии qt= sj, bj(Ot) = P(Ot | qt = sj).
Каждый элемент вложенной СММ называется суперсостояниеми представляет собой отдельную одномерную марковскую модель с параметрами, описанными выше.
Изображение с точки зрения распознавания
Цифровое изображение – суть случайный двумерный дискретный сигнал, наблюдаемый системой. Последовательность наблюдений (вектор наблюдений) может извлекаться из изображения различными способами. В силу этого описательные способности полученных моделей могут различаться. Наиболее предпочтительным является вариант сканирования изображения прямоугольным окном. Для уменьшения вероятности потери данных на границах блоков, рекомендуется сканировать изображение таким образом, что соседние блоки пикселей могут перекрываться друг другом. Значение перекрытия подбирается экспериментально.
Для снижения вычислительной сложности и уменьшения пространства признаков, каждый извлеченный блок пикселей подвергается некоторому преобразованию, в результате которого получается некоторый набор числовых данных, который и является вектором наблюдений.
Наиболее подходящими для поставленной задачи являются два преобразования:
- преобразование Карунена-Лоэва (англ. Karhunen-Loeve transform – сокр. KLT);
- дискретно-косинусное преобразование (англ. Discrete Cosine
Transform – сокр. DCT).
Далее, полученные вектора распределяются по состояниям модели. Здесь необходимо отметить, что каждая отдельная СММ представляет некоторый класс объектов. Тогда состояния модели определяют некоторые ключевые признаки класса. К примеру, СММ для поиска лиц состоит из 5 суперсостояний, соответствующих областям лица (лобовая часть, глаза, нос, рот, подбородок), каждое из которых делится на отдельные состояния.
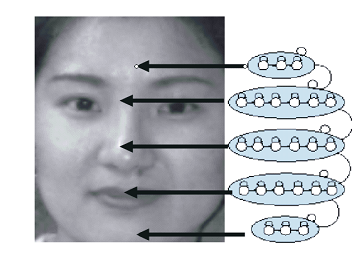
Переход в следующее состояние возможно только после предыдущего, а переход в следующее суперсостояние возможно только после всех состояний текущего суперсостояния. Вероятность принадлежности некоторого объекта заданному классу, оценивается как вероятность генерации сигнала, соответствующего его вектору признаков.
Поиск лиц
Предполагаем, что информация об изображениях коллекции хранится в какой-либо реляционной базе данных. Содержание изображений может быть определено на различных уровнях абстракции. На низшем уровне изображение представляет собой набор пикселей. Уровень пикселей редко используется в задаче поиска, так как это предполагает больших вычислительных и временных затрат.
Необработанные данные могут быть отправлены для генерации числовых дескрипторов, описывающих особенные визуальные характеристики, называемые сигнатурами. Как правило, уровень сигнатур изображения требует гораздо меньшего пространства, чем изображение.
Поиск изображений основан на поиске схожести в многомерном пространстве. При этом изображение определяется набором своих сигнатур. Мера схожести – это функция, которая вычисляет и возвращает значение, соответствующее схожести между двумя объектами согласно некоторым предопределенным критериям. Понятие меры сходства основывается на понятии метрики. Метрика – это функция расстояния d, определенная на метрическом множестве, для любых точек x, y, z которого
выполняются условия:
1.
 ,
,2.
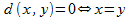 ,
,3.
 .
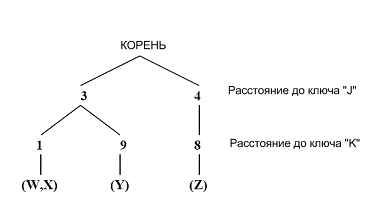
.Индексирование и поиск изображений в коллекциях производится на основе треугольного дерева (triangle tree, trie дерево), также называемое Really Fixed Query Tree. Треугольное дерево – это структура данных, разработанная для поиска приблизительных совпадений в зависимости от усилий поиска. Оно ассоциируется с мерой расстояния, набором ключевых изображений и набором элементов базы данных. Форма trie – это форма дерева, в котором ребра следуют от корня до листьев, определяя индекс листа. Листья дерева содержат элементы базы. Каждое внутреннее ребро в дереве ассоциируется с неотрицательным числом. Каждый уровень дерева ассоциируется с одиночным ключом. Путь от корня до листьев представляет собой расстояние от элемента базы данных до каждого из ключей.
На рисунке представлено треугольное дерево с 4 элементами (W, X, Y, Z) и 2 ключа (J, K). Расстояние от листа W до ключа J равно 3, расстояние от W до K равно 1. Таким образом, каждое изображение будет характеризоваться некоторым набором числовых значений, определенных как расстояния от этого изображения до существующих ключей.
Процесс индексирования изображений коллекции заключается в поиске расстояний от каждого изображения до каждого ключа. Исходя из вышесказанного, можно определить принцип поиска следующим образом. Пусть I представляет объект базы, Q представляет объект запроса, K представляет ключевые изображения и d определяет некоторые меры сходства – метрики. Используя свойство метрики (3), заключаем, что следующие неравенства будут верными:

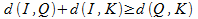
Комбинируя неравенства, получаем выражение, определяющее расстояние от объекта запроса до объекта коллекции:
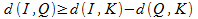
Таким образом, сравнивая объекты из базы данных и объекты запроса с третьим ключевым объектом, может быть получена нижняя граница дистанции между двумя объектами. На основе этой границы можно отсечь большую часть коллекции, как не удовлетворяющую запросу.
Также необходимо отметить, что процесс поиска происходит в два этапа. На первом этапе определяется нижняя граница расстояния от изображения запроса до изображений коллекции. На этой стадии происходит отсечение части коллекции. На втором этапе происходит уточняющий поиск: определяется расстояния от изображения-запроса до каждого изображения, из найденных на первой стадии. Изображения, соответствующие максимальным расстояниям, составляют итоговый результат поиска.
На основе вышесказанного можно сделать вывод, что для того, чтобы воспользоваться поиском и индексацией, для каждого изображения необходимо уметь производить следующие действия.
- Выделять сигнатуры изображений. Для одиночных изображений сигнатурой будут являться вектора наблюдений каждого лица, содержащихся на нем
- Выделять сигнатуры ключей. При этом для системы поиска на основе СММ, ключами будут являться наборы изображений одного лица, а сигнатурой параметры обученной на этих изображениях модели.
- Сравнивать сигнатуры ключа и изображения, а также два изображения. При этом результатом сравнения должно быть расстояние, выраженное целым числом, лежащим в отрезке [0; 99].
Вторая проблема заключается в том, что на данном этапе не представляется возможным использовать СММ для поиска расстояния между двумя отдельными изображениями. Это объясняется тем, что алгоритмы поиска требуют обученной модели: обучение модели на одном изображении является проблематичным.
При подготовке статьи использовались следующие материалы:
- Nefian, A.V. Hidden Markov Madel-Based Approach for Face Detection and Recognition / Ara Nefian. 1999.
- Джосан, О.В. Использование Скрытых Марковских Моделей для детектирования радужки на изображении лиц: 2006 / А.В. Джосан, МГУ им. Ломоносова. — 2006.
- Гультяева, Т.А. Скрытые марковские модели с одномерной топологией в задаче распознавания лиц / Т.А. Гультяева, А.А. Попов; НГТУ. — 2006.
- Berman, A.P. A Flexible Image Database System for Content-Based Retrieval: Computer Vision and Image Understanding / A.P. Berman, L.G. Shapiro. 1999.









