Тема бинарных деревьев уже обсуждалась на хабре (здесь и здесь).
Про AA-дерево было сказано, что «из-за дополнительного ограничения операции реализуются проще чем у красно-черного дерева (за счет уменьшения количества разбираемых случаев)».
Мне, однако, кажется, что AA-дерево заслуживает отдельной статьи.
Почему?
Потому, что фактически это самое быстрое (или одно из самых быстрых) бинарное дерево с простой реализацией.
Я оставлю за рамками данной статьи рассмотрение алгоритмов вставки и удаления в AVL и красно-черное дерево, но их реализация, как правило, не тривиальна. Почему?
Как известно, основная проблема бинарного дерева — его балансировка, то есть противодействие вырождению в обычный связный список. Обычно при балансировке дерева возникает много вариантов взаимного расположения вершин, каждый из которых нужно учесть в алгоритме отдельно.
AA-дерево было придумано Arne Andersson, который решил, что для упрощения балансировки дерева нужно ввести понятие уровень (level) вершины. Если представить себе дерево растущим сверху вниз от корня (то есть «стоящим на листьях»), то уровень любой листовой вершины будет равен 1. В своей работе Arne Andersson приводит простое правило, которому должно удовлетворять AA-дерево:
К одной вершине можно присоединить другую вершину того же уровня но только одну и только справа.
(В своей статье автор AA-дерева использует немного другую терминологию, связанную с 2-3 деревьями, но суть не меняется).
Таким образом, введенное понятие уровня вершины не всегда совпадает с реальной высотой вершины (расстояния от земли), но дерево сохраняет балансировку при следовании правилу «одна правая связь на одном уровне».
Для балансировки АА-дерева нужно всего 2 (две) операции.
Нетрудно их понять из правила «одна правая одноуровневая связь»: это устранение левой связи на одном уровне и устранение двух правых связей на одном уровне.
Это операции названы в оригинальной работе skew и split, соответственно. На приведенных рисунках горизонтальная стрелка обозначает связь между вершинами одного уровня, а наклонная (вертикальная) — между вершинами разного уровня.
skew, устранение левой связи на одном уровне
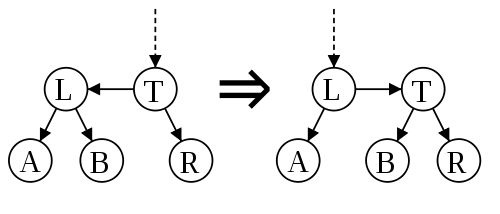
split, устранение двух правых связей на одном уровне
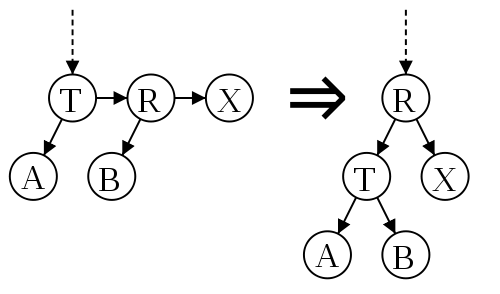
Давайте посмотрим как выглядит вставка и удаление в АА-дерево. Для упрощения реализации введем понятие вершины bottom ("земля"). Ее уровень всегда 0 и ее левая и правая связь указывают на нее же. Все листовые вершины ссылаются на bottom вместо того, чтобы хранить 0 в ссылке.
В рамках недель Delphi на Хабре, исходный код будет в виде псевдокода, похожего на Delphi (для влюбленных вкофе C++: операция P^.x в Delphi эквивалентна P->x, var означает что переменная передается по ссылке, а не по значению, т.е. при изменении меняется внешняя переменная).
Определим вершину AA-дерева.
Вставка элемента newkey проще всего выглядит в рекурсивной реализации.
Для вставки в дерево ключа newkey вызываем NodeInsert(root, newkey). Спускаемся от корня вниз по дереву, сравнивая ключи; вставляем; идем вверх и выполняем балансировку: skew и split для каждой вершины.
Удаление немного хитрее.
Используются две вспомогательные переменные — deleted и last. При спуске вниз по дереву (как и при вставке) сравниваются ключи вершин с удаляемым ключом. Если ключ вершины меньше удаляемого, то переходим к левой ссылке, иначе — к правой (т.е. к правой переходим даже при совпадении ключей). В last заносится каждая проходимая вершина, а в deleted — только та, где «свернули направо».
Когда достигнуто «дно» дерева, deleted указывает на вершину, в которой находится удаляемый ключ (если она есть в дереве), а last — на вершину, которую следует удалить (это может быть одна и та же вершина). Ключ переносится из last в deleted и вершина last удаляется.
Далее выполняется балансировка — нужно выполнить 3 skew и 2 split.
Реализация skew и split банальна.
Фактически, приведенный псевдокод достаточен для создания реализации АА-дерева (добавить лишь «мелочи» вроде модификации корня дерева (root) и пр.).
Некоторые полезные ссылки.
Реализация AA-дерева на C.
Замечательный апплет, в котором можно поиграться с различными видами деревьев (в том числе и с АА-деревьями).
Delphi проект с визуализацией АА-дерева и исходным кодом.
Статья в википедии.
Про AA-дерево было сказано, что «из-за дополнительного ограничения операции реализуются проще чем у красно-черного дерева (за счет уменьшения количества разбираемых случаев)».
Мне, однако, кажется, что AA-дерево заслуживает отдельной статьи.
Почему?
Потому, что фактически это самое быстрое (или одно из самых быстрых) бинарное дерево с простой реализацией.
Я оставлю за рамками данной статьи рассмотрение алгоритмов вставки и удаления в AVL и красно-черное дерево, но их реализация, как правило, не тривиальна. Почему?
Как известно, основная проблема бинарного дерева — его балансировка, то есть противодействие вырождению в обычный связный список. Обычно при балансировке дерева возникает много вариантов взаимного расположения вершин, каждый из которых нужно учесть в алгоритме отдельно.
AA-дерево было придумано Arne Andersson, который решил, что для упрощения балансировки дерева нужно ввести понятие уровень (level) вершины. Если представить себе дерево растущим сверху вниз от корня (то есть «стоящим на листьях»), то уровень любой листовой вершины будет равен 1. В своей работе Arne Andersson приводит простое правило, которому должно удовлетворять AA-дерево:
К одной вершине можно присоединить другую вершину того же уровня но только одну и только справа.
(В своей статье автор AA-дерева использует немного другую терминологию, связанную с 2-3 деревьями, но суть не меняется).
Таким образом, введенное понятие уровня вершины не всегда совпадает с реальной высотой вершины (расстояния от земли), но дерево сохраняет балансировку при следовании правилу «одна правая связь на одном уровне».
Для балансировки АА-дерева нужно всего 2 (две) операции.
Нетрудно их понять из правила «одна правая одноуровневая связь»: это устранение левой связи на одном уровне и устранение двух правых связей на одном уровне.
Это операции названы в оригинальной работе skew и split, соответственно. На приведенных рисунках горизонтальная стрелка обозначает связь между вершинами одного уровня, а наклонная (вертикальная) — между вершинами разного уровня.
skew, устранение левой связи на одном уровне
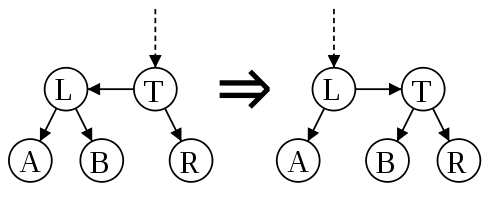
split, устранение двух правых связей на одном уровне
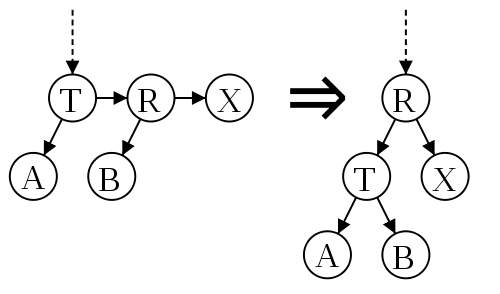
Давайте посмотрим как выглядит вставка и удаление в АА-дерево. Для упрощения реализации введем понятие вершины bottom ("земля"). Ее уровень всегда 0 и ее левая и правая связь указывают на нее же. Все листовые вершины ссылаются на bottom вместо того, чтобы хранить 0 в ссылке.
В рамках недель Delphi на Хабре, исходный код будет в виде псевдокода, похожего на Delphi (для влюбленных в
Определим вершину AA-дерева.
PNode = ^TNode;
TNode = packed record
left, right: PNode;
level: integer; // уровень; 1 у листьев
key: pointer; // ключ, данные связанные с вершиной
end;
Вставка элемента newkey проще всего выглядит в рекурсивной реализации.
procedure NodeInsert(var P: PNode; newkey: pointer);
begin
if P = bottom then begin // достигли "дна" - создаем новую вершину
new(P);
P^.left := bottom;
P^.right := bottom;
P^.level := 1;
P^.key := newkey;
end else begin
if newkey < P^.key then
NodeInsert(P^.left, newkey)
else if newkey > P^.key then
NodeInsert(P^.right, newkey)
else begin
P^.key := newkey;
exit;
end;
Skew(P);
Split(P);
end;
end;
Для вставки в дерево ключа newkey вызываем NodeInsert(root, newkey). Спускаемся от корня вниз по дереву, сравнивая ключи; вставляем; идем вверх и выполняем балансировку: skew и split для каждой вершины.
Удаление немного хитрее.
procedure NodeDelete(var P:PNode; newkey: pointer);
begin
if P <> bottom then begin
// 1. спускаемся вниз и запоминаем last и deleted
last := P;
if Compare(newkey, P) < 0 then // newkey < key
NodeDelete(P^.left, newkey)
else begin
deleted := P;
NodeDelete(P^.right, newkey);
end;
// 2. удаляем элемент, если найден
if (P = last) and (deleted <> bottom) and (newkey == deleted^.key) then begin
deleted^.key := P^.key;
deleted := bottom;
P := P^.right;
delete last;
end else if (P^.left.level < P^.level - 1) or (P^.right.level < P^.level - 1) then begin
// 3. выполняем балансировку при движении вверх
Dec(P^.level);
if P^.right.level > P^.level then P^.right.level := P^.level;
Skew(P);
Skew(P^.right);
Skew(P^.right^.right);
Split(P);
Split(P^.right);
end;
end;
end;
Используются две вспомогательные переменные — deleted и last. При спуске вниз по дереву (как и при вставке) сравниваются ключи вершин с удаляемым ключом. Если ключ вершины меньше удаляемого, то переходим к левой ссылке, иначе — к правой (т.е. к правой переходим даже при совпадении ключей). В last заносится каждая проходимая вершина, а в deleted — только та, где «свернули направо».
Когда достигнуто «дно» дерева, deleted указывает на вершину, в которой находится удаляемый ключ (если она есть в дереве), а last — на вершину, которую следует удалить (это может быть одна и та же вершина). Ключ переносится из last в deleted и вершина last удаляется.
Далее выполняется балансировка — нужно выполнить 3 skew и 2 split.
Реализация skew и split банальна.
// поменять местами _содержимое_ записей с вершинами (не указатели)
procedure Swap(P1, P2: PNode);
var
tmp: TNode;
begin
tmp := P1^;
P1^ := P2^;
P2^ := tmp;
end;
procedure Skew(T: PNode);
var
L: PNode;
begin
L := T^.left;
if T^.level = L^.level then begin
Swap(T, L); // теперь T ==> L, L ==> T
L^.left := T^.right; // т.е. T.left = L.right
T^.right := L; // т.е. L.right = T
end;
end;
procedure Split(T: PNode);
var
R: PNode;
begin
R := T^.right;
if T^.level = R^.right^.level then begin
Swap(T, R); // теперь T ==> R, R ==> T
R^.right := T^.left;
T^.left := R;
Inc(T^.level);
end;
end;
Фактически, приведенный псевдокод достаточен для создания реализации АА-дерева (добавить лишь «мелочи» вроде модификации корня дерева (root) и пр.).
Некоторые полезные ссылки.
Реализация AA-дерева на C.
Замечательный апплет, в котором можно поиграться с различными видами деревьев (в том числе и с АА-деревьями).
Delphi проект с визуализацией АА-дерева и исходным кодом.
Статья в википедии.






