Комментарии 52
выложи где-нибудь входящие данные
+2
файл данных, с которыми работаете.
0
Сигнал генерирую в 19 строчке. В принципе, если хотите, могу записать синусоиду в WAV, но зачем?
+1
то же самое в 1 команду


0
А еще pwelch, pmusic и т.д. Только топик был про нормировку вручную. MATLAB выбрал исключительно потому что без проблем визуализировать можно в одну команду.
+1
Одно но: визуализировать лучше в логарифмическом масштабе (в децибелах). Куда как нагляднее получится. Как у коллеги двумя комментами выше.
0
Выводил в линейном масштабе, чтобы явно было на входе 0.7 попугая и на спектре 0.7 попугая. А к какому основанию приводить попугаев в логарифмическом масштабе я не знаю.
+1
Ну как вы верно заметили, измеряется все равно в попугаях, так что принципиальной разницы нет, важны соотношения между гармониками и уровень шума. Вообще в подобных случаях чаще всего используется единица dBfs — приведение к полной шкале. То есть уровень синусоидального сигнала амплитудой 1 (к примеру) берется за 0 dBfs, а все остальное — ниже.
0
Вы слабо разбираетесь в теме. Не пудрите голову людям.
+1
Резко сказано… Но некоторые некорректности имеются.
Во-первых, на графике показаны как раз модули этих комплексных чисел, во-вторых нет такого понятия «амплитуда полосы частот», в-третьих комплексное число не имеет аргументов — он сам есть число и может являться аргументов. Если имеются в виду действительная и мнимая части, то их две, а начальная фаза у синусоиды одна. Что имелось в виду?
«следует учитывать, что счет алгоритма устроен таким образом, что перебираются не только положительные, но и отрицательные частоты»
Отрицательных частот не существует, а симметрия графика — есть результат нормализации (возведения в квадрат).
В качестве результата мы получим вектор комплексных чисел. Это и есть представление нашего сигнала в частотном домене в показательной форме. Т.е. модули этих комплексных чисел представляют амплитуды соответствующих частот (точнее полосы частот см. дальше), а аргументы – их начальные фазы.
Во-первых, на графике показаны как раз модули этих комплексных чисел, во-вторых нет такого понятия «амплитуда полосы частот», в-третьих комплексное число не имеет аргументов — он сам есть число и может являться аргументов. Если имеются в виду действительная и мнимая части, то их две, а начальная фаза у синусоиды одна. Что имелось в виду?
«следует учитывать, что счет алгоритма устроен таким образом, что перебираются не только положительные, но и отрицательные частоты»
Отрицательных частот не существует, а симметрия графика — есть результат нормализации (возведения в квадрат).
+3
Про график каюсь, надо бы указать, что строю именно амплитуды, собственно в самом скрипте видно, что я беру модуль.
На счет амплитуды — не смог сформулировать по-другому, но имеется ввиду суммарный уровень частот попавших в полосу (при этом не могу сказать что там прямо таки сумма).
Показательная форма представления комплексного числа — это не sin(x)-i*cos(x), а a*exp(i*phi), где а — модуль, а phi — аргумент, он же и будет начальной фазой (может стоит внести это пояснение в текст?).
На счет «отрицательных» частот, тоже вопрос для дискуссии. Я БПФ представляю как последовательный перебор корреляции сигнала с синусоидами различных частот начиная с отрицательных индексов. Физического смысла оно действительно не имеет, но в рамках алгоритма вполне себе живет.
На счет амплитуды — не смог сформулировать по-другому, но имеется ввиду суммарный уровень частот попавших в полосу (при этом не могу сказать что там прямо таки сумма).
Показательная форма представления комплексного числа — это не sin(x)-i*cos(x), а a*exp(i*phi), где а — модуль, а phi — аргумент, он же и будет начальной фазой (может стоит внести это пояснение в текст?).
На счет «отрицательных» частот, тоже вопрос для дискуссии. Я БПФ представляю как последовательный перебор корреляции сигнала с синусоидами различных частот начиная с отрицательных индексов. Физического смысла оно действительно не имеет, но в рамках алгоритма вполне себе живет.
+4
Я о том и говорю. Приветственная фраза обязывает излагать так, чтобы не вводить в заблуждение «юного читателя».
0
«Куда ставить-то?», в смысле, что поправить-то на ваш взгляд надо?
0
Если кроме меня к формулировкам так дотошно никто не относится, то особо нечего менять. Тут больше вопрос стиля, наверное.
Фраза «весьма сильно скрыт шумом» не очень хороша для технической публикации. Поэтично что ли… «Видны дискретные составляющие» — это тоже нехорошо. У вас же сам сигнал в дискретном времени, в нем каждый отсчет — дискретная составляющая. Легко ввести читателя в заблуждение, а знающим труднее понять. Можно же было так написать:
«Несмотря на то, что полезного сигнала не видно на фоне шума, спектральная характеристика позволяет определить его частоту и амплитуду.» Хотя и эта формулировка не безгрешна.
Как видно, несмотря на то, что сигнал весьма сильно скрыт шумом, в спектральном представлении все еще отчетливо видны дискретные составляющие (хоть и немного искаженные по амплитуде шумом).
Фраза «весьма сильно скрыт шумом» не очень хороша для технической публикации. Поэтично что ли… «Видны дискретные составляющие» — это тоже нехорошо. У вас же сам сигнал в дискретном времени, в нем каждый отсчет — дискретная составляющая. Легко ввести читателя в заблуждение, а знающим труднее понять. Можно же было так написать:
«Несмотря на то, что полезного сигнала не видно на фоне шума, спектральная характеристика позволяет определить его частоту и амплитуду.» Хотя и эта формулировка не безгрешна.
0
имеется ввиду суммарный уровень частот попавших в полосу (при этом не могу сказать что там прямо таки сумма
Это обобщенно и проще можно назвать энергией в данной элементарной полосе частот.
http://ru.wikipedia.org/wiki/%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%D1%82%D0%BE%D1%80_%D1%81%D0%BF%D0%B5%D0%BA%D1%82%D1%80%D0%B0
0
Да что такое… неудобно ссылки вставлять. Простите.
Анализатор спектра
Анализатор спектра
0
Только тут спектр амплитудный, а не энергический (для наглядности картинок делал), поэтому про энергию в полосе частот тоже говорить не корректно на мой взгляд.
0
А собственно почему не энергетический. Как раз на мой взгляд нечто похожее на гистограмму (по сути, не по внешнему виду). Нужно еще заметить, что по этим графикам нельзя определить был ли полезный сигнал на протяжении всего анализированного интервала времени одинаков по амплитуде. Его амплитуда могла быть как постоянной, так и меняться во времени. Это же графики квадратичных величин. Как раз энергии и есть. Но этим графикам исходный сигнал не восстановишь в первозданном виде. Каждый пик по сути это энергия соответствующего интервала частот (гармоник), приведенная к общей энергии спектрограммы (сигнала). У меня в свое время поэтому руки не доходили ответа на вопрос «в каких попугаях» построены эти графики. Потом вопрос утратил актуальность.
0
Это именно амплитудный спектр, если вы обратите внимание амплитуды пиков в спектре совпадают с заданными в качестве параметров. А если обратить внимание еще и на фазовый спектр (его не приводил в связи с непрезентабельностью), то можно в точности восстановить весь сигнал на протяжении всех 5 секунд. Собственно это и хотел показать, что пики находятся именно на своих местах и принимают реальные значения сигнала во временном домене безотносительно к типу сигнала (паскали, вольты, метры). А на счет изменения амплитуды со временем, так это уже модуляция, а спектр модулированного сигнала будет отличаться наличием гармоник модулирующего и это уже будет предметом анализа о чем речи в топике не идет.
0
А можно линк на тему того, как огибающая (кривая амплит. модуляции) появляется на спектрограмме?
+1
В случае синусоиды — пики вокруг модулируемого:
Амплитудная модуляция
Если огибающая сложнее — может быть совсем интересным.
Амплитудная модуляция
Если огибающая сложнее — может быть совсем интересным.
+1
Отрицательные частоты имеют вполне такой себе физический смысл. И в рамках очень простого эксперимента можно реально увидеть их на спектро-анализаторе. Возьмите и подайте на спектроанализатор последовательность прямоугольных видеоимпульсов, на картинке вы увидите спектр этой последовательности который будет представлять из себе 8ю картинку из этой статьи с максимальной частотой равной 0, и соответственно видеть мы будем только половину этого графика. Если мы начнем заполнять наш видеоимпульс несущей частотой то картинка, с ростом частоты начнет смещаться вправо по оси х. При несущих частотах близких к нулю левая от максимума(несущей частоты) часть графика будет отличаться от правой. Это потому, что в этой области частот происходит наложения двух частей спектра сигнала — спектра с положительной центральной частотой и спектра с отрицательной центральной частотой, правый хвост последнего (боковые лепестки) вылазит в область спектра положительных частот и в результате наложения левой части спектра с положительной центральной частотой и правой части спектра с отрицательной несущей частотой мы увидим не симметричный относительна несущей частоты спектр, а искаженный.
+1
Вот как я и говорил — ввели в заблуждение…
Задача для Буратино:
Малыш, представь, что у тебя в кармане три яблока и тут некто взял у тебя одно яблоко. Сколько у тебя в кармане яблок? Не торопись с ответом и учти, что в нашей школе принято отнимать от ответа «СТОПИЦЦОТ» штук.
Задача для Буратино:
Малыш, представь, что у тебя в кармане три яблока и тут некто взял у тебя одно яблоко. Сколько у тебя в кармане яблок? Не торопись с ответом и учти, что в нашей школе принято отнимать от ответа «СТОПИЦЦОТ» штук.
0
На всякий случай оговорюсь… Буратино — это я фильм детский вспомнил. Никого обзывать не собирался.
0
С Буратиной все ясно, но вот кого ввели в заблуждение я честно говоря не понял. Если меня то хотелось бы понять где я заблуждаюсь, да и в любом случае любые заблуждения нужно искоренять :)
0
Я про то, что линии на графике, строго говоря, не есть частоты, а лишь их изображение, интерпретация, визуализация. Какой же это физический смысл? То, что смещена ось частот на индикаторе не говорит об отрицательности частот. И если брать несущую частоту — ее близость к нулю (абсолютному, если не оговорено опять же смещение оси частот) означает близость несущего сигнала к постоянному. «Постояннее», чем постоянный сигнал, никакой сигнал быть не может. — Какой каламбур получился… Ужас.
На мой взгляд нельзя подменять парадигмы искусственно выведенными (производными) формулировками.
На мой взгляд нельзя подменять парадигмы искусственно выведенными (производными) формулировками.
+1
А я не говорил про графики. Я говорил про реальный спектроанализатор, и рассказал про эксперимент который позволяет ощутить реальность несуществующих отрицательных частот. Во как «реальность несуществующих»:)
0
«Наш преподаватель по физике, рассказывавший про эл/маг. волны, был настолько пьян, что мы реально увидели эти волны.
Какая разница какой индикатор? Растр/Вектор на экране монитора, подсвеченный люминесцентный экранчик осциллографа или любой другой?
Какая разница какой индикатор? Растр/Вектор на экране монитора, подсвеченный люминесцентный экранчик осциллографа или любой другой?
+1
Наверное тут имелась ввиду амплитудная модуляция, а не аддитивная смесь. Там реально возможна картинка с пиками, пляшущими вокруг несущей (и слева и справа). Только все же отрицательные частоты действительно не несут особого смысла, это тот же самый синус, но повернутый на 180 градусов.
-1
Можете в википедии почитать про Отрицательные частоты . Если вращается в одну сторону, то имеет положительную частоту, а если в другую, то отрицательную.
Получается, что частота вдруг превратилась в векторную величину и была частота сама по себе, а стала некоей относительной или зависимой.
Как профессиональный жаргон сойдет.
Получается, что частота вдруг превратилась в векторную величину и была частота сама по себе, а стала некоей относительной или зависимой.
Как профессиональный жаргон сойдет.
+1
«максимальной частотой равной 0» следует читать как «с максимумом в частоте равной нулю»
0
> Отрицательные частоты имеют вполне такой себе физический смысл. И в рамках очень простого эксперимента можно реально увидеть их на спектро-анализаторе.
Круто! На спектро-анализаторе!
А в природе нельзя?
Круто! На спектро-анализаторе!
А в природе нельзя?
-1
Не стал бы называть это некорректностями. Человек не знает что такое окно и зачем оно нужно в спектральном анализе. Код я смотрел нет там никакого окна. Кроме того, автор не понимает что спектр расплылся (при увеличении длины БПФ) не от «гармоник окна» а от некореектной (не кратной) передискретизации.
О таких мелочах как отсутствия связи с физическим временем, а как следствие некоррекнтое использование размерности (секунды, герцы) в изначально цифровом синале я молчу.
Всем минусующим карму пламенный привет.
О таких мелочах как отсутствия связи с физическим временем, а как следствие некоррекнтое использование размерности (секунды, герцы) в изначально цифровом синале я молчу.
Всем минусующим карму пламенный привет.
0
Вы точно читали статью и смотрели код? Целью топика было не объяснение особенностей методов уменьшения влияния краевых эффектов, а попытка показать, как можно убедиться, что результатом выполнения кода является именно то, что вы ожидаете увидеть. Сигнал генерировался относительно смоделированного времени. С заданными частотой дискретизации и длиной окна (фактически 5 секундное прямоугольное окно, или быть может вы предполагали, что я сгенерировал бесконечный сигнал?). И частоты приводились именно через частоту дискретизации сигнала.
А про карму, рискну предположить что кому-то не очень понравился «конструктивный» подход к написанию комментариев. Со своей стороны я бы тоже попросил больше конкретики, если я где-то заблуждаюсь укажите конкретно где, думаю не мне одному будет интересно выяснить какие-то детали которые я не понимаю или упускаю.
А про карму, рискну предположить что кому-то не очень понравился «конструктивный» подход к написанию комментариев. Со своей стороны я бы тоже попросил больше конкретики, если я где-то заблуждаюсь укажите конкретно где, думаю не мне одному будет интересно выяснить какие-то детали которые я не понимаю или упускаю.
0
Уххх как знакомо, у меня тема диплома была «Speech processing using DSP» — ну как то так, дословно уже не помню. Помучался я с этим ( pastebin.com/f12259e0d ) кодом…
x -> fft -> ifft -> profit
x -> fft -> ifft -> profit
+1
Добавьте пожалуйста в теги Фурье или преобразование Фурье, а то непонятно как люди искать потом этот топик будут, ведь главное тут не Матлаб, а алгоритм, о чём и говорит нам название блога =)
+1
Где вы были 4 дня назад… Когда я лабу писал
0
Хорошая статья, спасибо. Давно собирался поковырять MATLAB, вот будет повод.
Было время, FFT на C++ делал для дипломной. Тоже, помню, вылезли эти зеркальные отображения, физический смысл их так и не понял.
Было время, FFT на C++ делал для дипломной. Тоже, помню, вылезли эти зеркальные отображения, физический смысл их так и не понял.
0
Попробовал распознать ноту Ми (82.406 Гц). Получилось.
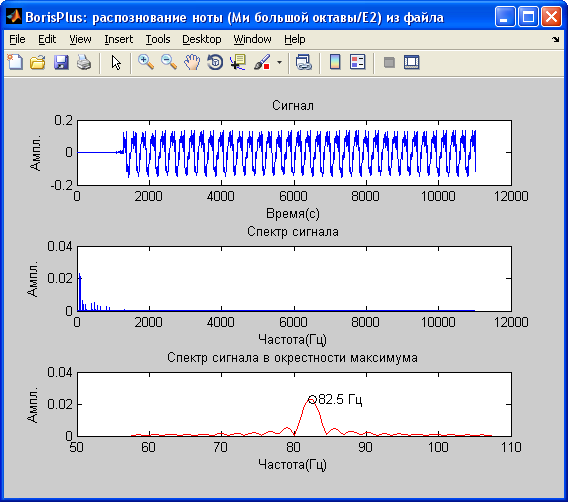
Есть мысль развить сие. Спасибо за толчок.

clear all% Очистка памяти
[Signal,hc,bits] = wavread('E2.wav');%Файл с длинным звучанием ноты
%% Параметры
Tm=0.5;% Длина сигнала (с)
Fd=hc;% Частота дискретизации (Гц), у меня была 22050 из wav характеритстика
FftL=Fd*2;% Количество линий Фурье спектра
Epsilon=50;% Окрестность максимальной частоты для наглядного графика n.3
Signal = transpose(Signal(1:(Fd*Tm)));% все же берем отрезок сигнала
%% Спектральное представление сигнала
FftS=abs(fft(Signal,FftL));% Амплитуды преобразования Фурье сигнала
FftS=2*FftS./FftL;% Нормировка спектра по амплитуде
FftS(1)=FftS(1)/2;% Нормировка постоянной составляющей в спектре
F=0:Fd/FftL:Fd/2-1/FftL;% Массив частот вычисляемого спектра Фурье
[C,i] = max(FftS);%Максимум и его аргумент вмассиве частот спектра
%% Построение графиков
figure( 'NumberTitle','off',...
'Name','BorisPlus: распознование ноты (Ми большой октавы/E2) из файла')
subplot(3,1,1);% Выбор области окна для построения
plot(Signal);% Построение сигнала
title('Сигнал');% Подпись графика
xlabel('Время(с)');% Подпись оси х графика
ylabel('Ампл.');% Подпись оси у графика
subplot(3,1,2);% Выбор области окна для построения
plot(F,FftS(1:length(F)));% Построение спектра Фурье сигнала
title('Спектр сигнала');% Подпись графика
xlabel('Частота(Гц)');% Подпись оси х графика
ylabel('Ампл.');% Подпись оси у графика
subplot(3,1,3);% Выбор области окна для построения
plot( F(max(1,i-Epsilon):min(length(F),i+Epsilon)),...
FftS(max(1,i-Epsilon):min(length(F),i+Epsilon)),'-r',...
F(i),FftS(i),'ko');% Посмотрим наглянее у максимума
title('Спектр сигнала в окрестности максимума');
xlabel('Частота(Гц)');% Подпись оси х графика
ylabel('Ампл.');% Подпись оси у графика
text(F(i)+1,FftS(i),[num2str(F(i)) ' ' 'Гц']);% Подпись точки максимума
Есть мысль развить сие. Спасибо за толчок.
0
Ну а теперь, чтоб было все просто красиво, как с подбором длинны иглы в опыте Бюффона, чтоб получить точное зачение Пи за одно-два бросания. Распознаем ноту Ля большой октавы (110 Гц). О-па! Чётко.
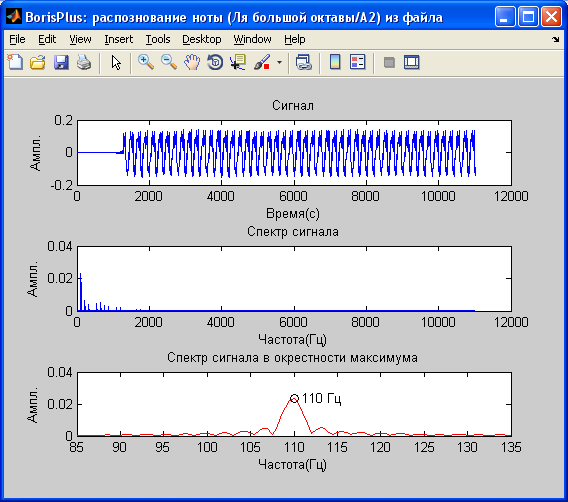

0
Лайк почему-то прожать не могу, но спасибо тебе, друг!
0
Зарегистрируйтесь на Хабре , чтобы оставить комментарий
MATLAB и быстрое преобразование Фурье