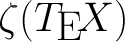 Демонстрируем некоторые особенности написания TeX-макросов, встраивая в TeX калькулятор теоретико-числовых функций.
Демонстрируем некоторые особенности написания TeX-макросов, встраивая в TeX калькулятор теоретико-числовых функций. Постановка задачи
Время от времени мне приходится набирать очередной текст, сопровождаемый примерами вычисления теоретико-числовых функций: функция Эйлера φ, функция делителей τ, функция Кармайкла λ. Раньше это делалось так: запускаем любимый калькулятор (мой выбор — PARI/GP), в нем все считаем и копируем выкладки в ТеХ. Изменились исходные данные — снова в калькулятор и обратно. Много возни, много шансов забыть заменить какой-то промежуточный результат. Да и просто мышкой махать надоедает. Хочется автоматизировать этот процесс хотя бы для самых распространенных функций, чтобы можно было написать
$\phi(1001)=\Phi(1001)$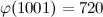
Самое общее решение — это использовать внешний препроцессор, который бы выкусывал нужные фрагменты формул, передавал их внешнему же калькулятору, забирал результат и вставлял его в документ. Главный минус — это, конечно, потеря совместимости. Раньше мы могли просто переслать tex-файл по электропочте. Теперь же, чтобы на том конце провода его можно было откомпилировать в pdf, нужна еще и подробная инструкция с указанием необходимых препроцессора и калькулятора. На этом этапе мы почти наверняка узнаем, что у получателя другая ОС и наши пляски с бубном ему даром не нужны. Переходим к плану Б.
План Б
Попробуем обойтись собственными средствами ТеХа, макросы которого, как известно, составляют Тьюринг-полный язык. Он не такой эзотерический, как Brainfuck, однако очень далек от Си-подобных синтаксиса и, хуже того, семантики.
Первое, что следует заметить, — это то, что макрос может принимать аргументы, но не может прозрачно возвращать значения. Паскалист сказал бы, что макрос ведет себя не как функция, а как процедура. Вот, например, как можно написать макрос, суммирующий два числа:
\newcount\s\def\addition#1#2{\s=#1\advance\s by#2 \number\s}Запутанно? Давайте попробуем еще раз, только с комментариями и пробелами:
\newcount\s % объявляем числовую переменную
\def\addition#1#2{ % объявляем макрос с двумя аргументами
\s=#1 % помещаем в s первый аргумент
\advance\s by#2 % прибавляем второй аргумент
\number\s % печатаем как число
}Теперь
2+3=\addition{2}{3}(Еще несколько примеров математических функций)
Деление нацело
Давайте напишем что-нибудь более сложное. Первая наша цель — функция, проверяющая, делится ли одно число на другое без остатка.
\newif\ifdivisible % объявляем булеву переменную
\newcount\testMod@n % объявляем числовую переменную
\def\testMod#1#2{ % объявляем макрос с двумя аргументами
\testMod@n=#1 % помещаем в testMod@n первый аргумент
\divide\testMod@n by#2 % делим нацело на второй аргумент
\multiply\testMod@n by#2 % и умножаем на него же
\ifnum#1=\testMod@n % если в результате получился снова первый аргумент,
\divisibletrue % значит остатка не было,
\else % а иначе
\divisiblefalse % был
\fi%
}Этот макрос помещает в divisible истину, если деление прошло без остатка, и ложь в противном случае. Проверяем:
\testMod{6}{3}
\ifdivisible 1 \else 0 \fi
\testMod{6}{4}
\ifdivisible 1 \else 0 \fi должно дать на выходе «1 0»: 6 делится на 3, но не делится на 4.
Если вы сохранили этот код в файл и собрали при помощи tex, то, наверное, уже увидели ошибку «TeX capacity exceeded». Дело в том, что мы забыли попросить рассматривать @ как обычный символ, допустимый в названиях макросов и переменных. Сделать это можно при помощи команды
\catcode `\@11Вообще, ТеХ умеет работать с областями видимости переменных и макросов, но делает это сильно не так, как принято в обычных языках программирования. Например, попытка
\def\addition{\newcount\s}\catcode `\@12Код, тестирующий \testMod
Унитарный делитель и возведение в степень
Следующий шаг: построим макрос, вычисляющий максимальную степень одного числа, которая все еще делит другое нацело (если d — простое, то это унитарный делитель):
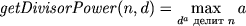
\newcount\divisorpower % здесь будем хранить текущее значение а,
\newcount\getDivisorPower@m % а здесь - n/d^a
\def\getDivisorPower#1#2{
\getDivisorPower@m=#1 % инициализируем переменные
\divisorpower=0 %
\testMod{\getDivisorPower@m}{#2} % проверяем, делится ли на d
\loop\ifdivisible % while-цикл, проверяющий условие divisible
\advance\divisorpower by1 % увеличиваем a на 1
\divide\getDivisorPower@m by#2 % делим на d
\testMod{\getDivisorPower@m}{#2} % снова проверяем, делится ли на d
\repeat % возвращаемся к началу цикла
}На Си этот код выглядел бы так (запишем его намеренно коряво):
int divisible;
int a;
int m;
void getDivisorPower(int n, int d){
m = n;
a = 0;
divisible = (m % d == 0);
while(divisible){
a++;
m /= d;
divisible = (m % d == 0);
}
}Теперь совсем легкий макрос:
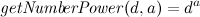
\newcount\numberpower % здесь будем хранить результат возведения в степень
\newcount\getNumberPower@pow % а здесь - сколько раз еще осталось умножить
\def\getNumberPower#1#2{
\numberpower=1 % инициализируем переменные
\getNumberPower@pow=#2
\loop\ifnum\getNumberPower@pow>0 % запускаем цикл
\multiply\numberpower by#1
\advance\getNumberPower@pow by-1
\repeat
}Снова на Си:
int numberpower;
int pow;
void getNumberPower(int d, int a){
numberpower = 1;
pow = a;
while(pow > 0){
numberpower *= d;
pow--;
}
}Можно было бы реализовать и более эффективный алгоритм возведения в степень, но нам хватит и такого.
Пора сделать проверку:
\getDivisorPower{600}{2}
\number\divisorpower
\getDivisorPower{600}{3}
\number\divisorpower
\getDivisorPower{600}{5}
\number\divisorpower
\getDivisorPower{600}{7}
\number\divisorpowerдолжно вывести «3 1 2 0», а
\getNumberPower{5}{0}
\number\numberpower
\getNumberPower{6}{1}
\number\numberpower
\getNumberPower{7}{2}
\number\numberpowerдаст «1 6 49».
Код, тестирующий \getDivisorPower и \getNumberPower
Что дальше?
Часть 2, в которой мы таки построим макрос, считающий функцию Эйлера. Для самых нетерпеливых — рабочая версия макроса. ТеХ легко справляется с расчетами при n~109.
Часть 3, в которой будут еще более навороченные примеры математических вычислений в ТеХе и, конечно же, бенчмарки.







