Здравствуй хабр.
Сегодня я хочу тебе рассказать про теорию когнитивного баланса Ф. Хайдера.
Сама теория относится к классу теорий когнитивного соответствия. При помощи этого класса теорий можно попытаться математически описать социальные взаимодействия, в том числе в социальных сетях.
Теория когнитивного баланса говорит, что человек по отношению к окружающему миру всегда находится либо в состоянии баланса, либо стремится к нему всеми возможными способами.
Изначальная модель имена название POX-модели и состояла из следующих компонентов:
Согласно этой теории отношение PO определяется также через отношения PX и OX следующим образом:

Например (из википедии), если P любит O; P не любит X; P знает, что X создал O; может привести P согласно этой теории к следующим возможным выводам:
Основываясь на этой модели, мы можем построить что-то свое, постепенно усложняя получившееся.
Итак, предположим, что:
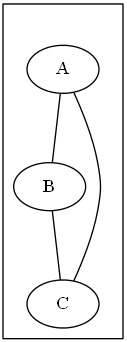
Если обозначить субъекты через вершины графа, а отношения между ними через дуги, то можно рассмотреть триаду следующего вида.
Теперь предположим, что отношения могут быть только позитивными (+) и негативными (-).
Тогда мы можем 8 возможных состояний нашей модели.
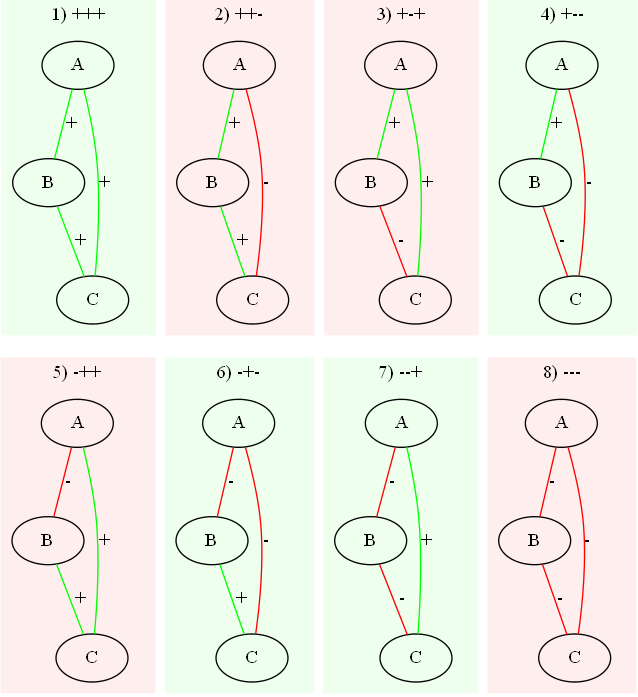
Существует утверждение о том, что триада является гармоничной, или устойчивой, если произведение знаков ее связей является положительным числом. То есть это возможно в случае, когда у нас 3 положительных связи, либо две отрицательных и одна положительная. То есть случаи 1,4,6,7 являются гармоничными и устойчивыми, а случаи 2, 3, 5, 8 неустойчивы.
В виде таблицы это будет выглядеть следующим образом.

Несбалансированные триады будут стремиться стать сбалансированными. У каждой из них есть три возможных варианта развития событий. Получаем так называемый куб переходов.
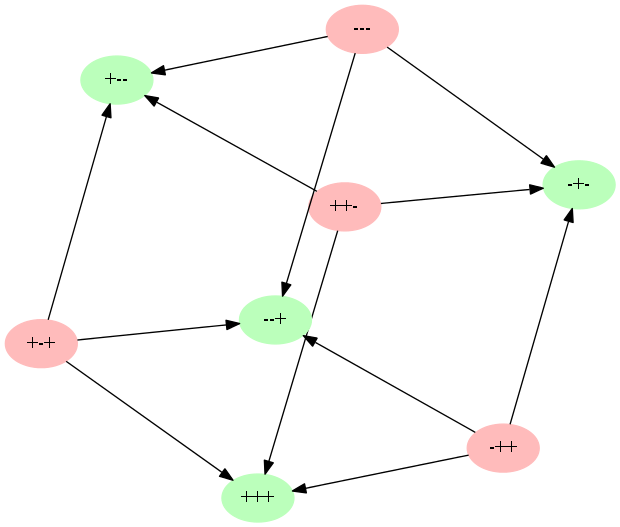
Причем варианты развития той или иной триады равновероятны.
Если внутри триады добавить нейтральные связи, то количество возможных состояний возрастет до 27. При этом 19 из них будут представлять собой вырожденные случаи, когда не все отношения установлены. В этом случае отсутствующие связи либо вообще не будут задействованы либо будут стремиться к описанным выше сбалансированным. С учетом этой информации куб переходов будет выглядеть следующим образом.

То есть, как и в первом случае получаем бинарное дерево триад и переходов между ними.
Если же веса отношений будут не равны друг другу, то вероятности перехода из одного состояния в другое будут разными, и мы сможем предсказать, как изменятся отношения внутри триады.
Но изолированные триады, как и сферические кони в вакууме могут быть только на бумаге. В реальном мире мы имеем более или менее крупный коллектив, внутри которого взаимодействия строятся по такому же принципу, что и внутри триад. В этом случае сбалансированность группы определяется сбалансированностью всех ее триад.
Из двух состояний групп то является более сбалансированным, в котором большее количество сбалансированных триад.
Для оценки сбалансированности группы можно ввести специальный индекс:
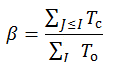
Где Tс – количество сбалансированных триад, Tо – общее количество триад.
Большие связанные подгруппы с высоким индексом сбалансированности внутри групп можно представлять в виде отдельного укрупненного субъекта, имеющего отношения со всеми остальными субъектами.
Существует структурная теорема, которая гласит, что большой граф (группа людей, объектов, отношений между ними) находится в сбалансированном состоянии тогда и только тогда, когда большая группа разделена на две малые подгруппы, внутри которых все связи положительны, а связи между группами отрицательны.
Действительно, если одну подгруппу мысленно разделить на две связные с большим положительным индексом, а вторую подгруппу оставить как есть, то получится классическая сбалансированная триада с одним плюсом и двумя минусами. Можно порассуждать на тему, что все субъекты могут иметь положительные отношения друг с другом, но вероятность такого исхода в 3 раза ниже, чем при разбиении на две конкурирующие подгруппы (триада №1 и триады №4, 6, 7 соответственно).
Если предположить, что в группе находится N человек, то число возможных отношений между ними будет составлять
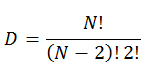
При условии, что у нас отношения могут быть положительными (+), отрицательными (-) и нейтральными (0), количество всех возможных состояний будет
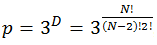
где общее количество триад будет

Следует так же учитывать, что самопроизвольные переходы при прочих равных, подчиняются следующим правилам.
С учетом этих условий для триады работает следующий куб переходов.
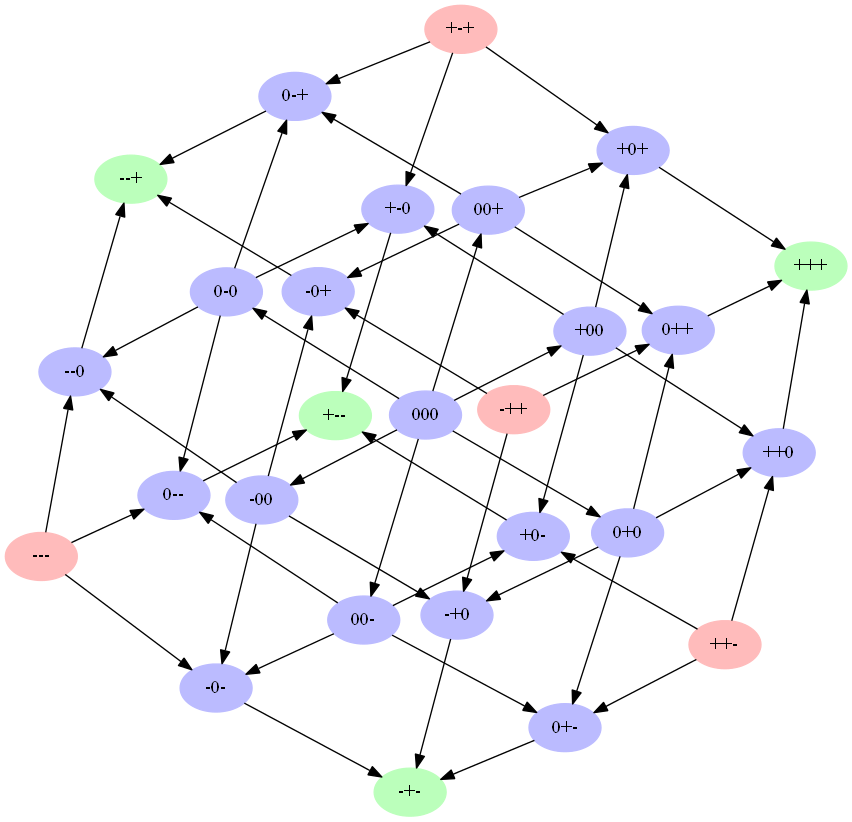
Так же на самопроизвольные переходы влияет количество сбалансированных триад, в которых человек принимает участие. Он стремится перейти в то состояние, в котором количество его сбалансированных триад увеличивается. В этом случае для определения вероятности такого перехода используется локальный индекс сбалансированности связи. Очевидно, что одно отношение не может принимать участие во всех возможных триадах группы. Поэтому для оценки используются только те триады, в которых эта связь принимает участие.
Тогда мы получаем
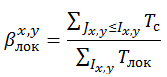
где Tс – сбалансированные триады для данной связи, Tлок – общее число триад для данной связи. Принцип оценки такой же, как и для целой группы.
Для полноты картины можно добавить более плавное изменение отношений – не просто положительное, отрицательное или нулевое, но и с каким либо весом r, заключенным в некотором промежутке. Например, в промежутке от -R до R, где R=0.5;1;5;10… В этом случае следует задать закон, по которому происходит изменение этих отношений. В ряде работ для этих целей используется гистерезис. В других работах учитывается понятие социальной дистанции.
В этом случае можно написать закон, по которому происходит изменение отношений с течением времени.

где G(r,R)=(1-(r/R))^2, а r(i,j) – отношение между i-м и j-м субъектами.
В качестве бонуса несколько анимированных гифок.
Внизу каждого изображения выводится общий индекс сбалансированности.
Для простой триады.
Даже не смотря на небольшие изначальные противоречия все трое дружны.

Двое дружат против третьего.

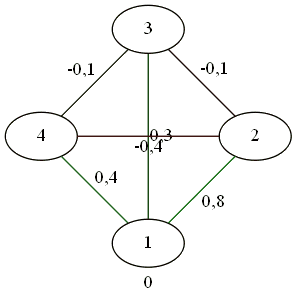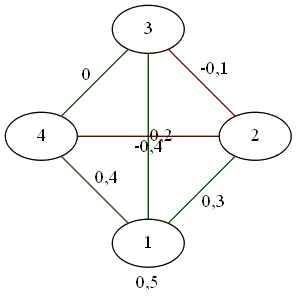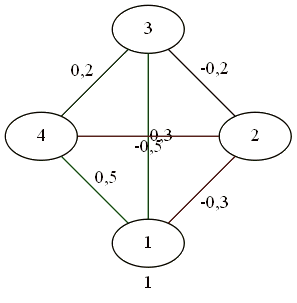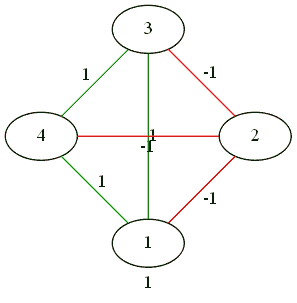
Для четверки.
Все дружат со всеми.

Противоборство 2 на 2.
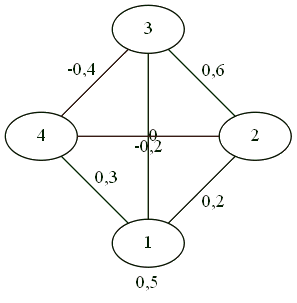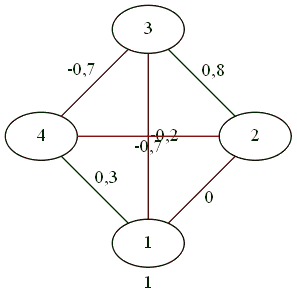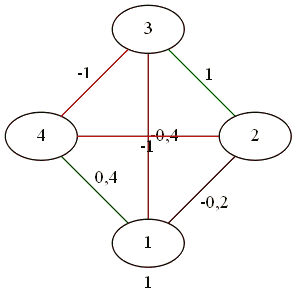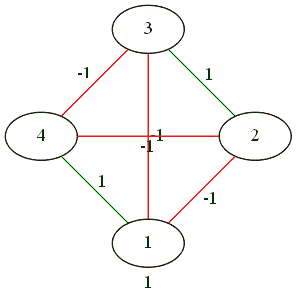
В результате сложных телодвижений трое против одного.
Чтобы не захламлять статью, остальные примеры можно посмотреть у меня в альбоме (для 5, 6, 10, и 25).
Хочу предупредить, что для большого количества персон получились увесистые гифки под 10 Мб.
И еще одно замечание. Программа прототип писалась на C#, для визуализации использовался Graphviz.
Так же при расчете триад можно учитывать состояние соседей второго, третьего и более высоких порядков. Разбивать на кластеры, объединять кластеры в одну большую персону. Можно учитывать то, что мы не всегда знаем всю информацию об отношениях между теми или иными субъектами. Или те или иные субъекты сами не обладают полнотой информации. Мы можем также использовать какое-то внешнее воздействие, или предположить что дуги могут иметь разный вес, или у одной из персон есть ресурсы для поддержания стабильно хороших отношений с какой-то другой персоной. Или их отсутствие. Можно рассмотреть пример выживания из изначально сбалансированной группы, и так далее.
В конце концов, мы можем вернуться к исходной модели и использовать орграф, то есть отношения между субъектами становятся несимметричными. В этом случае количество дуг удваивается, но принципы расчетов остаются теми же.
Впрочем, все это уже является темой гораздо более серьезного исследования.
Если кому-то интересно почитать на тему, то вот набор ссылок на работы, отталкиваясь от которых, я сделал эту статью.
На этом у меня все. Спасибо за внимание.
Ссылка 1
Ссылка 2
Ссылка 3
Ссылка 4
Ссылка 5
Сегодня я хочу тебе рассказать про теорию когнитивного баланса Ф. Хайдера.
Сама теория относится к классу теорий когнитивного соответствия. При помощи этого класса теорий можно попытаться математически описать социальные взаимодействия, в том числе в социальных сетях.
Теория когнитивного баланса говорит, что человек по отношению к окружающему миру всегда находится либо в состоянии баланса, либо стремится к нему всеми возможными способами.
Вводная часть
Изначальная модель имена название POX-модели и состояла из следующих компонентов:
- P – это некоторая личность;
- O – некий объект (в том числе и личность), по отношению к которому эта личность P – испытывает какие-то отношения в формате нравится/не нравится;
- X – некая другая личность, по отношению к которой P испытывает некие отношения, и которая сама по отношению к объекту O испытывает тоже некоторые отношения и P об этом знает.
Согласно этой теории отношение PO определяется также через отношения PX и OX следующим образом:
- Друг моего друга мой друг.
- Друг моего врага мой враг.
- Враг моего друга мой враг.
- Враг моего врага мой друг.

Например (из википедии), если P любит O; P не любит X; P знает, что X создал O; может привести P согласно этой теории к следующим возможным выводам:
- X – не такой уж и плохой
- O – не такой уж и хороший
- X – не автор O.
Основываясь на этой модели, мы можем построить что-то свое, постепенно усложняя получившееся.
Итак, предположим, что:
- У нас есть 3 неких субъекта: A, B и C.
- У всех субъектов есть отношения друг к другу, причем эти отношения обоюдные (это позволяет перейти от орграфа к просто графу и упростить начальную модель).
Если обозначить субъекты через вершины графа, а отношения между ними через дуги, то можно рассмотреть триаду следующего вида.

Теперь предположим, что отношения могут быть только позитивными (+) и негативными (-).
Тогда мы можем 8 возможных состояний нашей модели.
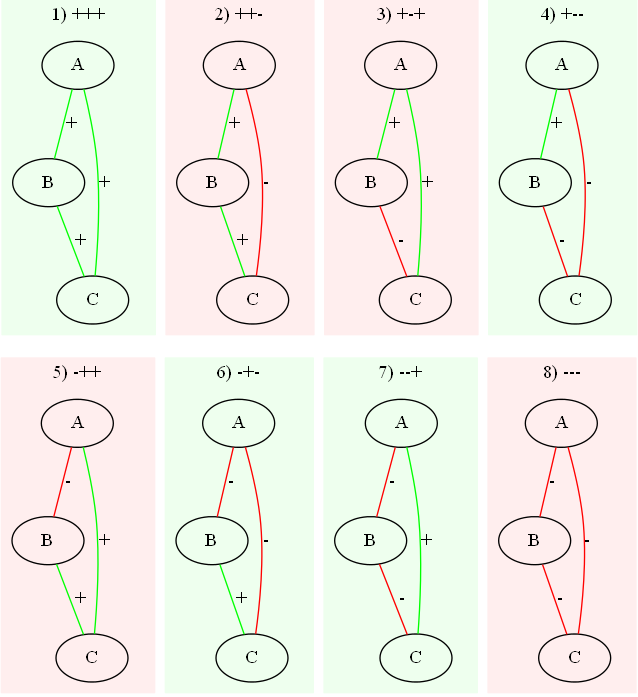
Существует утверждение о том, что триада является гармоничной, или устойчивой, если произведение знаков ее связей является положительным числом. То есть это возможно в случае, когда у нас 3 положительных связи, либо две отрицательных и одна положительная. То есть случаи 1,4,6,7 являются гармоничными и устойчивыми, а случаи 2, 3, 5, 8 неустойчивы.
В виде таблицы это будет выглядеть следующим образом.

Несбалансированные триады будут стремиться стать сбалансированными. У каждой из них есть три возможных варианта развития событий. Получаем так называемый куб переходов.
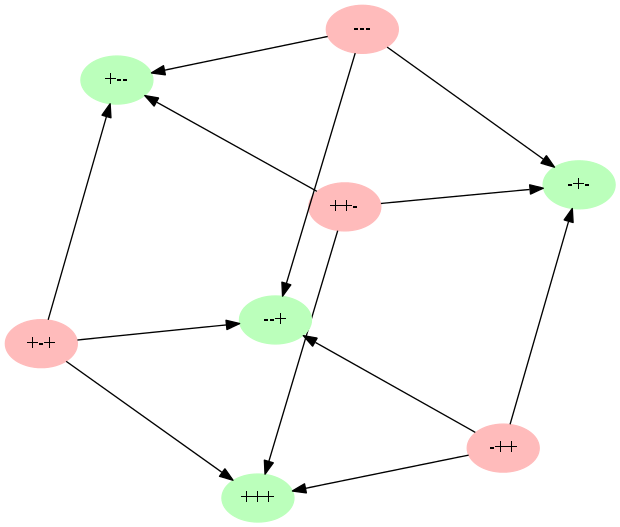
Причем варианты развития той или иной триады равновероятны.
Если внутри триады добавить нейтральные связи, то количество возможных состояний возрастет до 27. При этом 19 из них будут представлять собой вырожденные случаи, когда не все отношения установлены. В этом случае отсутствующие связи либо вообще не будут задействованы либо будут стремиться к описанным выше сбалансированным. С учетом этой информации куб переходов будет выглядеть следующим образом.

То есть, как и в первом случае получаем бинарное дерево триад и переходов между ними.
Если же веса отношений будут не равны друг другу, то вероятности перехода из одного состояния в другое будут разными, и мы сможем предсказать, как изменятся отношения внутри триады.
Но изолированные триады, как и сферические кони в вакууме могут быть только на бумаге. В реальном мире мы имеем более или менее крупный коллектив, внутри которого взаимодействия строятся по такому же принципу, что и внутри триад. В этом случае сбалансированность группы определяется сбалансированностью всех ее триад.
Из двух состояний групп то является более сбалансированным, в котором большее количество сбалансированных триад.
Немного формул
Для оценки сбалансированности группы можно ввести специальный индекс:
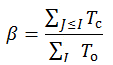
Где Tс – количество сбалансированных триад, Tо – общее количество триад.
Большие связанные подгруппы с высоким индексом сбалансированности внутри групп можно представлять в виде отдельного укрупненного субъекта, имеющего отношения со всеми остальными субъектами.
Существует структурная теорема, которая гласит, что большой граф (группа людей, объектов, отношений между ними) находится в сбалансированном состоянии тогда и только тогда, когда большая группа разделена на две малые подгруппы, внутри которых все связи положительны, а связи между группами отрицательны.
Действительно, если одну подгруппу мысленно разделить на две связные с большим положительным индексом, а вторую подгруппу оставить как есть, то получится классическая сбалансированная триада с одним плюсом и двумя минусами. Можно порассуждать на тему, что все субъекты могут иметь положительные отношения друг с другом, но вероятность такого исхода в 3 раза ниже, чем при разбиении на две конкурирующие подгруппы (триада №1 и триады №4, 6, 7 соответственно).
Если предположить, что в группе находится N человек, то число возможных отношений между ними будет составлять
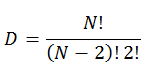
При условии, что у нас отношения могут быть положительными (+), отрицательными (-) и нейтральными (0), количество всех возможных состояний будет
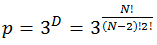
где общее количество триад будет

Следует так же учитывать, что самопроизвольные переходы при прочих равных, подчиняются следующим правилам.
- Вероятность самопроизвольного перехода отношений (0)→(+) и (0)→(-) близка к единице.
- Вероятность самопроизвольного перехода отношений (+)→(0), (-)→(0), (+)→(-), (-)→(+) близка к нулю.
С учетом этих условий для триады работает следующий куб переходов.
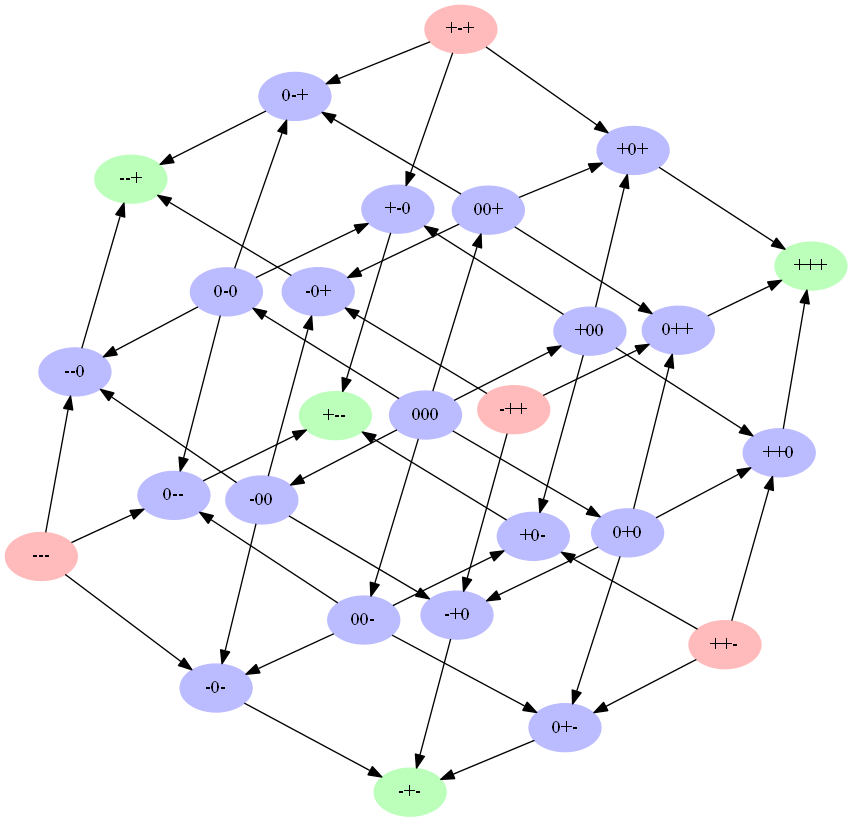
Так же на самопроизвольные переходы влияет количество сбалансированных триад, в которых человек принимает участие. Он стремится перейти в то состояние, в котором количество его сбалансированных триад увеличивается. В этом случае для определения вероятности такого перехода используется локальный индекс сбалансированности связи. Очевидно, что одно отношение не может принимать участие во всех возможных триадах группы. Поэтому для оценки используются только те триады, в которых эта связь принимает участие.
Тогда мы получаем

где Tс – сбалансированные триады для данной связи, Tлок – общее число триад для данной связи. Принцип оценки такой же, как и для целой группы.
Для полноты картины можно добавить более плавное изменение отношений – не просто положительное, отрицательное или нулевое, но и с каким либо весом r, заключенным в некотором промежутке. Например, в промежутке от -R до R, где R=0.5;1;5;10… В этом случае следует задать закон, по которому происходит изменение этих отношений. В ряде работ для этих целей используется гистерезис. В других работах учитывается понятие социальной дистанции.
В этом случае можно написать закон, по которому происходит изменение отношений с течением времени.

где G(r,R)=(1-(r/R))^2, а r(i,j) – отношение между i-м и j-м субъектами.
Примеры
В качестве бонуса несколько анимированных гифок.
Внизу каждого изображения выводится общий индекс сбалансированности.
Для простой триады.
Даже не смотря на небольшие изначальные противоречия все трое дружны.

Двое дружат против третьего.

Для четверки.
Все дружат со всеми.

Противоборство 2 на 2.

В результате сложных телодвижений трое против одного.

Чтобы не захламлять статью, остальные примеры можно посмотреть у меня в альбоме (для 5, 6, 10, и 25).
Хочу предупредить, что для большого количества персон получились увесистые гифки под 10 Мб.
И еще одно замечание. Программа прототип писалась на C#, для визуализации использовался Graphviz.
Так же при расчете триад можно учитывать состояние соседей второго, третьего и более высоких порядков. Разбивать на кластеры, объединять кластеры в одну большую персону. Можно учитывать то, что мы не всегда знаем всю информацию об отношениях между теми или иными субъектами. Или те или иные субъекты сами не обладают полнотой информации. Мы можем также использовать какое-то внешнее воздействие, или предположить что дуги могут иметь разный вес, или у одной из персон есть ресурсы для поддержания стабильно хороших отношений с какой-то другой персоной. Или их отсутствие. Можно рассмотреть пример выживания из изначально сбалансированной группы, и так далее.
В конце концов, мы можем вернуться к исходной модели и использовать орграф, то есть отношения между субъектами становятся несимметричными. В этом случае количество дуг удваивается, но принципы расчетов остаются теми же.
Впрочем, все это уже является темой гораздо более серьезного исследования.
Если кому-то интересно почитать на тему, то вот набор ссылок на работы, отталкиваясь от которых, я сделал эту статью.
На этом у меня все. Спасибо за внимание.
Ссылка 1
Ссылка 2
Ссылка 3
Ссылка 4
Ссылка 5






