Я расскажу о структуре под названием дерево отрезков и приведу его простую реализацию на языке С++. Эта структура весьма полезна в случаях, когда необходимо часто искать значение какой-то функции на отрезках линейного массива и иметь возможность быстро изменять значения группы подряд идущих элементов.
Типичный пример задачи на дерево отрезков:
Есть линейный массив, изначально заполненный некоторыми данными. Далее приходят 2 типа запросов:
1й тип — найти значение максимального элемента на отрезке массива [a..b].
2й тип — заменить iй элемент массива на x.
Возможен запрос «добавить х ко всем элементам на отрезке [a..b]», но в данной статье я его не рассматриваю.
С помощью дерева отрезков можно искать не только максимум чисел, но и любую функцию, удовлетворяющую свойству ассоциативности.
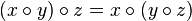
Это ограничение связано с тем, что используется предпросчет значений для некоторых отрезков.
Так же можно искать, например, не значения, а порядковые номера элементов.
Желательно, что бы функция имела «нейтральный» аргумент, который не оказывает влияния на результат. Например, для суммы это число 0: (a + 0 = a), а для максимума это бесконечность: max(a, -inf) = a.
Итак, поехали.
Самый простой (и медленный) способ решать представленную выше задачу, это завести линейный массив, и покорно делать то, что от нас хотят.
при такой реализации время нахождения ответа на запрос имеет порядок О(n). в среднем, придется пройтись по половине массива что бы найти максимум. Хотя есть и положительные моменты — изменение значения какого-либо элемента требует O(1) времени. Этот алгоритм можно ускорить в 2 раза, если выполнить небольшой предпросчет: для каждой пары элементов найдем значение максимального из них, и запишем в другой массив. Тогда при поиске максимума на отрезке, для каждой пары элементов уже известно значение большего, и сравнивать придется только с ним. остается только аккуратно проверить граничные элементы, так как граница запрашиваемого отрезка не обязательно четная.
На рисунке выделены элементы, которые необходимо проверять.

Понятно, что над этими массивами можно ввести еще один, что бы поиск был еще в 2 раза быстрее, а над ним еще один… и так до тех пор, пока самый верхний массив не будет состоять из одного элемента. Как не трудно догадаться, значение единственного элемента в самом верхнем массиве – это значение максимального элемента.

Некоторые пояснения: число рядом с вершиной дерева — это положение этой вершины в реальном массиве. При такой реализации хранения дерева очень удобно искать предка и потомков вершины: предок вершины i имеет номер i/2, а потомки номера i*2 и i*2+1. Из рисунка видно, что необходимо, что бы длинна массива была степенью двойки. Если это не так, то массив можно в конце дополнить нейтральными элементами. Расход памяти на хранение структуры от 2n до 4n, (n — количество элементов).
Алгоритм поиска «сверху» (есть еще и «снизу») весьма прост и в понимании и в реализации (хотя тех, кто не знаком с рекурсией, это всё может озадачить).
Алгоритм таков:
Начинаем опрос с вершины 1 (самая верхняя).
1.пусть текущая вершина знает максимум на промежутке l..r.
«пересекаются области [a..b] и [l..r] ?»
возможные варианты:
a. вообще не пересекаются.
что бы не влиять на результат вычисления, вернем нейтральный элемент (-бесконечность).
b. область [l..r] полностью лежит внутри [a..b].
вернуть предпросчитанное значение в текущей вершине.
с. другой вариант перекрытия областей.
спросить то же самое у детей текущей вершины и вычислить максимум среди них (смотрите код, если непонятно).
Как видно, алгоритм короткий, но рекурсивный. Временная сложность O(logN), что намного луче, чем О(N). например, при массиве длинной 10^9 элементов, необходимо примерно 32 сравнения.
Изменить число в этой структуре еще проще — надо пройти по всем вершинам от заданной до 1й, и если значение в текущей меньше чем новое, то заменить его. Это так же занимает O(log N) времени.
Реализация алгоритма.
Предполагается, что количество элементов массива не более 1024 (номера 0..1023).
Вот, в общем, и все, что необходимо в первую очередь знать о дереве отрезков.
Для разнообразия можно еще разобраться с алгоритмом вычисления «снизу» (он, кстати, нерекурсивный), хотя я нахожу его менее симпатичным. Ну и, конечно же, стоит разобраться с быстрым добавлением суммы ко всем элементам на отрезке (тоже за O(log N)), но это будет слишком утомительно для человека, который впервые разбирается с деревом отрезков.
Типичный пример задачи на дерево отрезков:
Есть линейный массив, изначально заполненный некоторыми данными. Далее приходят 2 типа запросов:
1й тип — найти значение максимального элемента на отрезке массива [a..b].
2й тип — заменить iй элемент массива на x.
Возможен запрос «добавить х ко всем элементам на отрезке [a..b]», но в данной статье я его не рассматриваю.
С помощью дерева отрезков можно искать не только максимум чисел, но и любую функцию, удовлетворяющую свойству ассоциативности.
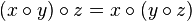
Это ограничение связано с тем, что используется предпросчет значений для некоторых отрезков.
Так же можно искать, например, не значения, а порядковые номера элементов.
Желательно, что бы функция имела «нейтральный» аргумент, который не оказывает влияния на результат. Например, для суммы это число 0: (a + 0 = a), а для максимума это бесконечность: max(a, -inf) = a.
Итак, поехали.
Самый простой (и медленный) способ решать представленную выше задачу, это завести линейный массив, и покорно делать то, что от нас хотят.
при такой реализации время нахождения ответа на запрос имеет порядок О(n). в среднем, придется пройтись по половине массива что бы найти максимум. Хотя есть и положительные моменты — изменение значения какого-либо элемента требует O(1) времени. Этот алгоритм можно ускорить в 2 раза, если выполнить небольшой предпросчет: для каждой пары элементов найдем значение максимального из них, и запишем в другой массив. Тогда при поиске максимума на отрезке, для каждой пары элементов уже известно значение большего, и сравнивать придется только с ним. остается только аккуратно проверить граничные элементы, так как граница запрашиваемого отрезка не обязательно четная.
На рисунке выделены элементы, которые необходимо проверять.

Понятно, что над этими массивами можно ввести еще один, что бы поиск был еще в 2 раза быстрее, а над ним еще один… и так до тех пор, пока самый верхний массив не будет состоять из одного элемента. Как не трудно догадаться, значение единственного элемента в самом верхнем массиве – это значение максимального элемента.

Некоторые пояснения: число рядом с вершиной дерева — это положение этой вершины в реальном массиве. При такой реализации хранения дерева очень удобно искать предка и потомков вершины: предок вершины i имеет номер i/2, а потомки номера i*2 и i*2+1. Из рисунка видно, что необходимо, что бы длинна массива была степенью двойки. Если это не так, то массив можно в конце дополнить нейтральными элементами. Расход памяти на хранение структуры от 2n до 4n, (n — количество элементов).
Алгоритм поиска «сверху» (есть еще и «снизу») весьма прост и в понимании и в реализации (хотя тех, кто не знаком с рекурсией, это всё может озадачить).
Алгоритм таков:
Начинаем опрос с вершины 1 (самая верхняя).
1.пусть текущая вершина знает максимум на промежутке l..r.
«пересекаются области [a..b] и [l..r] ?»
возможные варианты:
a. вообще не пересекаются.
что бы не влиять на результат вычисления, вернем нейтральный элемент (-бесконечность).
b. область [l..r] полностью лежит внутри [a..b].
вернуть предпросчитанное значение в текущей вершине.
с. другой вариант перекрытия областей.
спросить то же самое у детей текущей вершины и вычислить максимум среди них (смотрите код, если непонятно).
Как видно, алгоритм короткий, но рекурсивный. Временная сложность O(logN), что намного луче, чем О(N). например, при массиве длинной 10^9 элементов, необходимо примерно 32 сравнения.
Изменить число в этой структуре еще проще — надо пройти по всем вершинам от заданной до 1й, и если значение в текущей меньше чем новое, то заменить его. Это так же занимает O(log N) времени.
Реализация алгоритма.
Предполагается, что количество элементов массива не более 1024 (номера 0..1023).
- #include <cstdio>
- #include <algorithm>
-
- using namespace std;
- #define INF 1000000000 // предпологаем, что чисел больше такого не будет.
-
- #define TREE_REAL_DATA 1024 // максимальное допустимое количество элементов
- int tree_data[TREE_REAL_DATA * 2];
-
- // основная функция поиска.
- // аргументы: p - текушая вершина(пронумерованы согласно рисунку).
- // l, p - левая и правая границы отрезка, для которого tree_data[p] является максимумом.
- // вообще можно было обойтись без этих параметров, и определять их исходя из p, но так проще и понятней.
- // a, b - левая и правая границы отрезка, для которого необходимо найти минимум.
- int __tree_find_max(int p, int l, int r, int a, int b)
- {
- if (b < l || r < a) return -INF;
- if (a <= l && r <= b) return tree_data[p];
- int r1 = __tree_find_max(p*2 , l, (l+r) / 2, a, b); // опрос левого предка
- int r2 = __tree_find_max(p*2+1, (l+r)/2 + 1, r, a, b); // опрос правого предка
- return max(r1, r2); // нахождение большего из левого и правого поддеревьев
- }
-
- // более юзабильная оболочка для функции выше.
- int tree_find_max(int a, int b)
- {
- return __tree_find_max(1, 0, TREE_REAL_DATA - 1, a, b);
- }
-
- // обновление элемента № р.
- void tree_update(int p, int x)
- {
- p += TREE_REAL_DATA; // преобразование позиции p к позиции в самом нижнем массве,
- // в котором реально находится массив со значениями.
- tree_data[p] = x;
- for(p/=2; p ; p/=2) {
- if (tree_data[p * 2] > tree_data[p * 2 + 1])
- tree_data[p] = tree_data[p * 2];
- else tree_data[p] = tree_data[p * 2 + 1];
- }
- }
-
- // простейшая инициализация - установка всех значений в -INF
- void tree_init()
- {
- for (int i = 0; i < TREE_REAL_DATA * 2; i++)
- tree_data[i] = -INF;
- }
-
- int main()
- {
- tree_init();
- while ( 1 ){
- char c;
- scanf("%c", &c);
- if (c == 'Q') return 0; // выход
- if (c == 'F') { // найти максимум на интервале a..b
- int a, b;
- scanf("%d%d", &a, &b);
- printf("%d\n", tree_find_max(a, b));
- }
- if (c == 'U') { // установить значение элемента p равым x.
- int p, x;
- scanf("%d%d", &p, &x);
- tree_update(p, x);
- }
- }
- }
-
-
Вот, в общем, и все, что необходимо в первую очередь знать о дереве отрезков.
Для разнообразия можно еще разобраться с алгоритмом вычисления «снизу» (он, кстати, нерекурсивный), хотя я нахожу его менее симпатичным. Ну и, конечно же, стоит разобраться с быстрым добавлением суммы ко всем элементам на отрезке (тоже за O(log N)), но это будет слишком утомительно для человека, который впервые разбирается с деревом отрезков.






