Новости из мира науки: матрицы размера 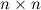 теперь умеют умножать за
теперь умеют умножать за 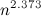 . Другими словами, доказано, что
. Другими словами, доказано, что 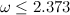 , где
, где 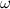 — экспонента умножения матриц. Доказала это совсем недавно Вирджиния Василевска-Вильямс, улучшив тем самым оценку
— экспонента умножения матриц. Доказала это совсем недавно Вирджиния Василевска-Вильямс, улучшив тем самым оценку 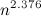 , полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты Скотта Ааронсона, Ричарда Липтона и Билла Гасарша.
, полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты Скотта Ааронсона, Ричарда Липтона и Билла Гасарша.
Итак, многие теоретические верхние оценки на время работы алгоритмов используют экспоненту умножения матриц. В частности, много алгоритмов на графах эксплуатируют данную идею: если A — матрица смежности графа, то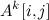 — количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время
— количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время 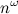 проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
Ещё несколько примеров:
 теперь умеют умножать за
теперь умеют умножать за 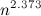 . Другими словами, доказано, что
. Другими словами, доказано, что 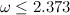 , где
, где 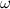 — экспонента умножения матриц. Доказала это совсем недавно Вирджиния Василевска-Вильямс, улучшив тем самым оценку
— экспонента умножения матриц. Доказала это совсем недавно Вирджиния Василевска-Вильямс, улучшив тем самым оценку 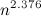 , полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты Скотта Ааронсона, Ричарда Липтона и Билла Гасарша.
, полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты Скотта Ааронсона, Ричарда Липтона и Билла Гасарша.Итак, многие теоретические верхние оценки на время работы алгоритмов используют экспоненту умножения матриц. В частности, много алгоритмов на графах эксплуатируют данную идею: если A — матрица смежности графа, то
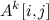 — количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время
— количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время 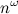 проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.Ещё несколько примеров:
- Расстояния между всеми парами вершин (all-pairs shortest path).
Кратчайшие пути между всеми парами вершин в невзвешенном графе можно найти за время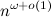 . Для этого возводим матрицу смежности в степень n (отсюда и вылезает o(1) в степени), попутно подсчитывая кратчайшие пути. Узнать подробности, а также много других подобных элегантных алгоритмов можно из
. Для этого возводим матрицу смежности в степень n (отсюда и вылезает o(1) в степени), попутно подсчитывая кратчайшие пути. Узнать подробности, а также много других подобных элегантных алгоритмов можно из
отличнейшей презентации Ури Цвика. - Задача максимальной 2-выполнимости (MAX-2-SAT).
Единственный известный алгоритм для этой задачи, который работает быстрее, чем полный перебор (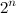 ), тоже основан на умножении матриц. Его время работы равно
), тоже основан на умножении матриц. Его время работы равно  и он использует экспоненциальную память. В двух словах идея такая: по входной формуле строим огромный граф (на
и он использует экспоненциальную память. В двух словах идея такая: по входной формуле строим огромный граф (на  вершинах) и с помощью быстрого умножения матриц проверяем, есть ли в нём треугольник. Примечательно, что придумал его муж Вирджинии — Раян Вильямс.
вершинах) и с помощью быстрого умножения матриц проверяем, есть ли в нём треугольник. Примечательно, что придумал его муж Вирджинии — Раян Вильямс. - Гамильтонов путь (Hamiltonian cycle).
Ещё есть такой забавный пример, в котором не так важно, за сколько мы умеем умножать матрицы, но всё же. Алгоритм для поиска гамильтонова пути за время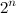 и полиномиальную память (отметим, что известный алгоритм Хелда-Карпа для этой задачи основан на динамическом программировании и требует экспоненциальной памяти): он вычисляет число путей длины n-1 на всех подмножествах вершин графа с помощью обозначенного выше трюка; после этого формула включений-исключений позволяет просуммировать найденные числа так, чтобы осталось лишь число простых путей длины n-1 (а это и есть гамильтоновы пути).
и полиномиальную память (отметим, что известный алгоритм Хелда-Карпа для этой задачи основан на динамическом программировании и требует экспоненциальной памяти): он вычисляет число путей длины n-1 на всех подмножествах вершин графа с помощью обозначенного выше трюка; после этого формула включений-исключений позволяет просуммировать найденные числа так, чтобы осталось лишь число простых путей длины n-1 (а это и есть гамильтоновы пути).
 . Для этого возводим матрицу смежности в степень n (отсюда и вылезает o(1) в степени), попутно подсчитывая кратчайшие пути. Узнать подробности, а также много других подобных элегантных алгоритмов можно из
. Для этого возводим матрицу смежности в степень n (отсюда и вылезает o(1) в степени), попутно подсчитывая кратчайшие пути. Узнать подробности, а также много других подобных элегантных алгоритмов можно из 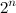 ), тоже основан на умножении матриц. Его время работы равно
), тоже основан на умножении матриц. Его время работы равно  и он использует экспоненциальную память. В двух словах идея такая: по входной формуле строим огромный граф (на
и он использует экспоненциальную память. В двух словах идея такая: по входной формуле строим огромный граф (на  вершинах) и с помощью быстрого умножения матриц проверяем, есть ли в нём треугольник. Примечательно, что придумал его муж Вирджинии — Раян Вильямс.
вершинах) и с помощью быстрого умножения матриц проверяем, есть ли в нём треугольник. Примечательно, что придумал его муж Вирджинии — Раян Вильямс.








