Комментарии 61
Не хватает ссылки на википедию или краткого описания применения, потому что до этого я даже не знал что это и где применяется.
Да уж, понятно, что хабр и все такое, но можно было в первом абзаце хотя бы пару предложений об этом Делоне, а потом уж с места в карьер.
Это первый мой пост. И я просто думал, что мой пост будут читать люди подкрепленные знаниями в теории двухмерной графики. И что изначально им знакомы все эти термины. Исправлюсь в следующем посте. Спасибо.
А можно воспользоваться тем фактом что триангуляция Делоне взаимно-однозначно соответсвует диаграмме Вороного и одним проходом решить задачу по заметанию плоскости например при помощи sweep line алгоритма
www.diku.dk/hjemmesider/studerende/duff/Fortune/
Или может я что-то упускаю?
www.diku.dk/hjemmesider/studerende/duff/Fortune/
Или может я что-то упускаю?
Все правильно. Задачу можно решить при помощи диаграммы Вороного, конечно. Но «sweep line» алгоритм достаточно беспощаден к времени. В частности найти пересечение трех парабол — очень ресурсоемко.
Ммм… там вроде не параболы, там гиперболы. Не могу сказать что мне до конца понятен этот алгоритм, но насколько можно судить из описания сложность математических операций там небольшая.
Триангуляция Делоне для отрезков строится проще, чем диаграмма Вороного для отрезков. Вычислительная сложность алгоритмов, конечно, одинакова (я не имею в виду предложенный автором статьи алгоритм).
Операций сложения в последней формуле не 8, а 14 (6 тратится на перенос системы координат). И непонятно еще, сколько чего придется потратить на проверку выпуклости четырехугольника. Может быть, через углы все-таки проще?
А так, да, все красиво. И есть над чем подумать.
А так, да, все красиво. И есть над чем подумать.
Углы не проще: точно сравнить сумму углов со 180 градусами будет очень сложно, а неточные сравнения могут привести к трэшу в результирующем ответе. Посмотрите, например, статью Шевчука: Adaptive precision arithmetic. Мы с вами здесь же на Хабре, вроде, обсуждали мою статью как раз на эту тему :)
Почему сложно? Проверяется знак мнимой части произведения четырех комплексных чисел. Если он будет вычисляться с ошибкой, то и другие численные методы (включая знак объема тетраэдра с вершинами на параболоиде) дадут не меньшую ошибку (а то и бОльшую — за счет бОльшего числа операций). А там — применять интервальную арифметику, двоично-рациональные числа большой точности, или писать алгоритм так, чтобы ошибка не приводила к проблемам. Ну, будет одна из точек чуть внутри окружности, ну и что: Лишь бы глобальные инварианты, используемые в алгоритме, от этого не нарушались.
Да, каюсь, пролетел мимо комментария, где вы пользуетесь комплексными числами для сумм углов, и мысль пошла в сторону тригонометрии.
Забавно: если раскрыть скобки в вашем выражении для сумм углов через комплексные числа, получится ровно та же формула, что и у автора статьи и в определителе системы координат аффинного пространства. Этого, конечно, следовало ожидать. В любом случае, число операций везде будет одинаковым (с точностью до расстановки скобок).
Забавно: если раскрыть скобки в вашем выражении для сумм углов через комплексные числа, получится ровно та же формула, что и у автора статьи и в определителе системы координат аффинного пространства. Этого, конечно, следовало ожидать. В любом случае, число операций везде будет одинаковым (с точностью до расстановки скобок).
Да с количеством операций погорячился. Спасибо, что заметили. Их действительно 14. Но они мало влияют на результат.
Проверку выпуклости отдельно проверять не нужно(как правило). При решении с помощью уравнения окружности эта задача отпадает. Чтобы 4-ехугольник был выпуклым, достаточно чтобы точка лежала вне исследуемого треугольника, и внутри описанной окружности. 1-ое условие — на входе. А если 2-ое не выполняется, то и перестраивать, получается, не надо. Идем к следующему треугольнику.
Проверку выпуклости отдельно проверять не нужно(как правило). При решении с помощью уравнения окружности эта задача отпадает. Чтобы 4-ехугольник был выпуклым, достаточно чтобы точка лежала вне исследуемого треугольника, и внутри описанной окружности. 1-ое условие — на входе. А если 2-ое не выполняется, то и перестраивать, получается, не надо. Идем к следующему треугольнику.
Что-то подозрительно. Вот вы проверяете принадлежность точки M кругу (ABC). Какие конкретно треугольники при этом анализируются?
Понял. ABC и CBM. Поскольку M и A лежат по разные стороны от прямой BC, то внутрь сегмента AB точка M попасть не может.
Но тогда и с углами проверки не нужны. Перестройка потребуется, если сумма углов BAC и CMB больше 180, а в этом случае углы MBA и ACM заведомо меньше 180.
Но тогда и с углами проверки не нужны. Перестройка потребуется, если сумма углов BAC и CMB больше 180, а в этом случае углы MBA и ACM заведомо меньше 180.
Все правильно. Но все равно у меня реализация с углами не работала.
Как-то так?
Для треугольников 123 и 134:
Интересно, в каких случаях она не работает.
Для треугольников 123 и 134:
u12=x1-x2; v12=y1-y2;
u32=x3-x2; v32=y3-y2;
u14=x1-x4; v12=y1-y4;
u34=x3-x4; v32=y3-y4;
re2=u12*u32+v12*v32;
im2=u12*v32-v12*u32;
re4=u14*u34+v14*v34;
im4=v14*u34-u14*v34;
return re2*im4+im2*re4<0; // если true, то перестраиваем.
Интересно, в каких случаях она не работает.
Кстати, я этого способа раньше не замечал. Спасибо.
Да этот способ! Вам спасибо!
С помощью быстрого умножения комплексных чисел можно сэкономить еще два умножения (обменяв их на 6 сложений):
Вместо
написать:
и аналогично для re4, im4.
Вместо
re2=u12*u32+v12*v32;
im2=u12*v32-v12*u32;
написать:
w1=u12*v32; w2=v12*u32;
re2=(u12+v12)*(u32+v32)-w1-w2;
im2=w1-w2;
и аналогично для re4, im4.
И по позже обязательно разберусь почему. Истина познается в обсуждении.
Нет не анализируются.
Если взять любые две пары треугольников образующих четырехугольник, то окажется что они априори выпуклые.
Иначе на этом месте было бы не два а уже три треугольника.
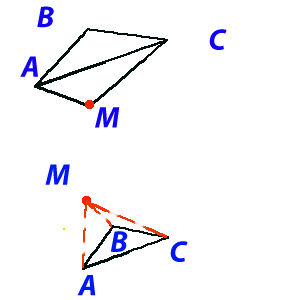
Если взять любые две пары треугольников образующих четырехугольник, то окажется что они априори выпуклые.
Иначе на этом месте было бы не два а уже три треугольника.
Андрей, если позволите, сделаю пару замечаний:
1. Вы описали что-то очень похожее на ушную триангуляцию. Насколько я понимаю, в худшем случае у вас время работы алгоритма кубическое (ушную триангуляцию, правда, можно довести до квадратичного времени). Если я прав, то все очень печально: триангуляция Делоне с ограничениями (constrained Delaunay triangulation) работает за O(N log N), а избавиться от лишних диагоналей можно за линейное время. Или я невнимательно прочитал вашу статью?
2. Критерий Делоне проверяется в библиотеках вычислительной геометрии исходя из следующих соображений: представьте себе треугольник T на плоскости P. Погрузим эту плоскость в трехмерное пространство и возьмем ортонормированную систему координат, в которой два орта лежат на плоскости P. Допустим, это будут орты x и y. Орт z, соответственно, будет перпендикулярен плоскости P. Рассмотрим параболоид z = r^2, где r — радиус-вектор точки на плоскости (линейная комбинация x и y). Оказывается, что любая окружность на плоскости, спроецированная на такой параболоид будет содержаться в некоторой плоскости, секущей параболоид на две части. Соответственно, точка, лежащая внутри окружности, будет ниже плоскости, а точка вне окружности — выше. Учитывая, что точки треугольника лежат на описанной около этого треугольника окружности, легко составить предикат, проверяющий критерий Делоне для четырех точек: это будет знак определителя системы координат, составленной из этих точек, спроецированных на параболоид в трехмерном пространстве. В общем, расписав определитель такой матрицы (это просто выписанные построчно однородные координаты точек), вы получите свой же результат с той лишь разницей, что он обобщается на Евклидовское пространство любой конечной размерности :)
Вообще, рекомендую воспользоваться библиотекой вычислительной геометрии, чтобы не искать множество любопытных ошибок (например, связанных с устойчивостью вычислений). Попробуйте посмотреть на CGAL или LEDA.
1. Вы описали что-то очень похожее на ушную триангуляцию. Насколько я понимаю, в худшем случае у вас время работы алгоритма кубическое (ушную триангуляцию, правда, можно довести до квадратичного времени). Если я прав, то все очень печально: триангуляция Делоне с ограничениями (constrained Delaunay triangulation) работает за O(N log N), а избавиться от лишних диагоналей можно за линейное время. Или я невнимательно прочитал вашу статью?
2. Критерий Делоне проверяется в библиотеках вычислительной геометрии исходя из следующих соображений: представьте себе треугольник T на плоскости P. Погрузим эту плоскость в трехмерное пространство и возьмем ортонормированную систему координат, в которой два орта лежат на плоскости P. Допустим, это будут орты x и y. Орт z, соответственно, будет перпендикулярен плоскости P. Рассмотрим параболоид z = r^2, где r — радиус-вектор точки на плоскости (линейная комбинация x и y). Оказывается, что любая окружность на плоскости, спроецированная на такой параболоид будет содержаться в некоторой плоскости, секущей параболоид на две части. Соответственно, точка, лежащая внутри окружности, будет ниже плоскости, а точка вне окружности — выше. Учитывая, что точки треугольника лежат на описанной около этого треугольника окружности, легко составить предикат, проверяющий критерий Делоне для четырех точек: это будет знак определителя системы координат, составленной из этих точек, спроецированных на параболоид в трехмерном пространстве. В общем, расписав определитель такой матрицы (это просто выписанные построчно однородные координаты точек), вы получите свой же результат с той лишь разницей, что он обобщается на Евклидовское пространство любой конечной размерности :)
Вообще, рекомендую воспользоваться библиотекой вычислительной геометрии, чтобы не искать множество любопытных ошибок (например, связанных с устойчивостью вычислений). Попробуйте посмотреть на CGAL или LEDA.
Спасибо, огромное! Расширили кругозор.
Пожалуйста. Вообще, эти рассуждения показывают связь между триангуляцией Делоне и выпуклой оболочкой: триангуляция Делоне — это проекция выпуклой оболочки спроецированных на параболоид исходных точек.
А что насчет вычислительной сложности предложенного вами алгоритма?
А что насчет вычислительной сложности предложенного вами алгоритма?
Интересует смысл фразы"… а избавиться от лишних диагоналей можно за линейное время". Можете разжевать? Что имеется ввиду. Чтобы до конца Вас понять.
Спорить об обобщении вычислительной сложности не буду, потому что сам не до конца понимаю его смысл. Разве что — прикинуть.Все равно все зависит от конкретной реализации. И уже ее стоит сравнивать с другими по сложности. Конкретную сложность в худшем случае, посчитать это одно. На практике как правило, все работает совсем иначе. Как видно из условия моей задачи, нужно построить триангуляцию с ограничениями. И даже не просто с ограничениями, а каждая точка уже в самом начале имеет две связи. При вставке новой прямой, проверять на пересечение с другими(оставшимися) прямыми все равно придется. От этой нагрузки по моему не избавиться. Но она первая и последняя из критичных.
Спорить об обобщении вычислительной сложности не буду, потому что сам не до конца понимаю его смысл. Разве что — прикинуть.Все равно все зависит от конкретной реализации. И уже ее стоит сравнивать с другими по сложности. Конкретную сложность в худшем случае, посчитать это одно. На практике как правило, все работает совсем иначе. Как видно из условия моей задачи, нужно построить триангуляцию с ограничениями. И даже не просто с ограничениями, а каждая точка уже в самом начале имеет две связи. При вставке новой прямой, проверять на пересечение с другими(оставшимися) прямыми все равно придется. От этой нагрузки по моему не избавиться. Но она первая и последняя из критичных.
Имеется в виду, что если запустить алгоритм построения триангуляции Делоне на множестве отрезков, то результатом будет фактически триангуляция выпуклой оболочки множества отрезков. Значит, у вас, скорее всего, появятся лишние диагонали, их нужно будет убрать. Это делается за линейное время (O(N)).
С вычислительной сложностью имеет смысл разобраться (почитайте, например, статью в википедии). Просто предлагать оптимизации к кубическому алгоритму для решения задачи при условии, что она решается за O(N log N) так же странно, как, например, пытаться где-то экономить копейки при регулярных бессмысленных милионных тратах :) Это не имхо. Вы можете попытаться прикинуть ожидаемую вычислительную сложность (как бы для «среднего случая»), но сделать это будет достаточно сложно, а в вашем случае, по-видимому, и бесполезно.
С вычислительной сложностью имеет смысл разобраться (почитайте, например, статью в википедии). Просто предлагать оптимизации к кубическому алгоритму для решения задачи при условии, что она решается за O(N log N) так же странно, как, например, пытаться где-то экономить копейки при регулярных бессмысленных милионных тратах :) Это не имхо. Вы можете попытаться прикинуть ожидаемую вычислительную сложность (как бы для «среднего случая»), но сделать это будет достаточно сложно, а в вашем случае, по-видимому, и бесполезно.
Статья в вики с вычислительной сложностью мало помогает — на предлагает поверить на слово, что среднее число флипов равно O(1). А без этого понять, действительно ли там O(n*log(n)), не получится. И как, например, изменится сложность, если точки добавлять не случайно, а отсортированными по x (чтобы убрать проблему поиска области)? Для выпуклой 2D оболочки она сразу дает гарантированное n*log(n). А для триангуляции?
1. Насколько я понял, автор не знает, что такое вычислительная сложность вообще. Тут я предложил википедию: как мне кажется, для начала ее вполне хватит.
2. Расчет вычислительной сложности триангуляции Делоне описывается у того же Скворцова (хотя на мой взгляд лучше читать книгу по вычислительной геометрии де Берга, Овермарса и др.). И таки да, среднее число флипов действительно равно O(1). Это выглядит достоверным даже на первый взгляд: степень вершин триангуляции в среднем равна шести (следствие теоремы Эйлера), хотя, конечно, строгое доказательство несколько сложнее.
Что касается сортировки точек в лексикографическом порядке — фактически в алгоритмах триангуляции Делоне заметающей прямой базовый шаг производит сортировку точек. Суммарные затраты на выталкивание точки из очереди с приоритетом и будут давать этот O(N*log N). Модификация алгоритма, использующая начальную сортировку тривиальна и никакого значения не имеет.
3. Позанудствую, конечно, но, строго говоря, для выпуклой оболочки точек плоскости верхняя граница вычислительной сложности O(N log H), где H — число вершин выпуклой оболочки. См. алгоритм Чена.
2. Расчет вычислительной сложности триангуляции Делоне описывается у того же Скворцова (хотя на мой взгляд лучше читать книгу по вычислительной геометрии де Берга, Овермарса и др.). И таки да, среднее число флипов действительно равно O(1). Это выглядит достоверным даже на первый взгляд: степень вершин триангуляции в среднем равна шести (следствие теоремы Эйлера), хотя, конечно, строгое доказательство несколько сложнее.
Что касается сортировки точек в лексикографическом порядке — фактически в алгоритмах триангуляции Делоне заметающей прямой базовый шаг производит сортировку точек. Суммарные затраты на выталкивание точки из очереди с приоритетом и будут давать этот O(N*log N). Модификация алгоритма, использующая начальную сортировку тривиальна и никакого значения не имеет.
3. Позанудствую, конечно, но, строго говоря, для выпуклой оболочки точек плоскости верхняя граница вычислительной сложности O(N log H), где H — число вершин выпуклой оболочки. См. алгоритм Чена.
O(N log H) — обязательно посмотрю. Если бы H было максимальным числом вершин промежуточных выпуклых оболочек, можно было бы поверить. Но организовать построение так, чтобы в промежуточных оболочках никогда не было вершин больше, чем const*«число вершин в итоговой оболочке» — интересно, как.
1. Комментарий про N log H относился к выпуклым оболочкам вообще. Понятно, что точки, спроецированные на параболоид (да и вообще на любую выпуклую поверхность), будут вершинами выпуклой оболочки.
2. Стоп. Каких промежуточных оболочек? У меня ощущение, что вы пытаетесь построить инкрементальный алгоритм триангуляции Делоне через выпуклые оболочки. Зачем? Инкрементальный алгоритм построения выпуклой оболочки работает так: на каждом шаге у нас есть корректная триангуляция Делоне и структура для локализации очередной точки в триангуляции, позволяющая найти треугольник, содержащий точку за O(log N). Дальше серия флипов, равная, в конечном счете, степени свежедобавленной вершины. Ниже вы приводите интересный пример облома инкременальной триангуляции. И действительно, таких примеров море. Фокус в том, что первый шаг любого инкрементального алгоритма — рандомная перестановка начальных данных. Таким образом, вероятность получения именно такого порядка на конкретно ваших данных равна 1/N!.. В среднем для всех перестановок число флипов будет O(1).
2. Стоп. Каких промежуточных оболочек? У меня ощущение, что вы пытаетесь построить инкрементальный алгоритм триангуляции Делоне через выпуклые оболочки. Зачем? Инкрементальный алгоритм построения выпуклой оболочки работает так: на каждом шаге у нас есть корректная триангуляция Делоне и структура для локализации очередной точки в триангуляции, позволяющая найти треугольник, содержащий точку за O(log N). Дальше серия флипов, равная, в конечном счете, степени свежедобавленной вершины. Ниже вы приводите интересный пример облома инкременальной триангуляции. И действительно, таких примеров море. Фокус в том, что первый шаг любого инкрементального алгоритма — рандомная перестановка начальных данных. Таким образом, вероятность получения именно такого порядка на конкретно ваших данных равна 1/N!.. В среднем для всех перестановок число флипов будет O(1).
2. Вы же сами пишете, что N*log(H) — про выпуклые оболочки. Вот и я про них. Да, пока я пытаюсь понять, можно ли добиться такой сложности в рамках инкрементальных алгоритмов. Хотя знаю, что могут быть и другие подходы.
2а. Так O(N*log(N)) это не гарантированная, а средняя сложность? Тогда другое дело. Я так понимал, что они знают алгоритм с гарантированным O(n*log(n)) (как для выпуклой оболочки).
2а. Так O(N*log(N)) это не гарантированная, а средняя сложность? Тогда другое дело. Я так понимал, что они знают алгоритм с гарантированным O(n*log(n)) (как для выпуклой оболочки).
2. Алгоритм Чена (O(N log H)) — статический алгоритм на плоскости, то есть все вершины обрабатываются скопом.
Но еще раз: это все неважно для построения триангуляции Делоне с помощью выпуклых оболочек, так как все точки в любой момент времени всегда будут вершинами выпуклой оболочки.
2a. Часто в динамических и инкрементальных алгоритмах берут именно среднюю сложность, так как сложность в худшем случае сильно хуже :) Для триангуляции Делоне есть статические алгоритмы, работающие гарантированно за O(N log N). Например, построение триангуляции с использованием заметающей прямой.
Но еще раз: это все неважно для построения триангуляции Делоне с помощью выпуклых оболочек, так как все точки в любой момент времени всегда будут вершинами выпуклой оболочки.
2a. Часто в динамических и инкрементальных алгоритмах берут именно среднюю сложность, так как сложность в худшем случае сильно хуже :) Для триангуляции Делоне есть статические алгоритмы, работающие гарантированно за O(N log N). Например, построение триангуляции с использованием заметающей прямой.
Средняя степень, может быть, и 6 (правда, плоскость можно заполнить треугольниками так, что степень каждой вершины будет какой угодно — хоть неограниченно возрастающей — и это будет триангуляция Делоне — но для конечного множества допустим, что в среднем 6). Но кто мешает каждой добаляемой точке временно (в момент ее добавления) иметь большую степень? Например: возьмем K лучей из одного центра, на каждом K точек (расстояния до центра — 1-1/(n+2), где n — номер точки в множестве: x=(n+1)/(n+2)*cos(2*pi*n/K), y=(n+1)/(n+2)*sin(2*pi*n/K). Будем (совершенно случайно, естественно) добавлять точки по спирали, начиная с самых внешних. По-моему, каждую новую точку придется соединить со всеми последними точками на лучах, т.е. она потребует порядка K флипов. Хотя надо будет проверить.
Извините, я знаю что такое вычислительная сложность. Иначе какой я программист. Просто, говорю еще раз, на практике очень сложно представить «худший случай» в реальности. Т.е. на практике обычно алгоритмы покывают другие результаты. Все во многом еще зависит от входящих данных. Например, иногда нет смысла переходить к 3D, если все прозрачно и в 2D. Мы можем больше времени потратить на перевод из 2D в 3D и обратно, плюс я не говорю еще о большей вычислительной нагрузке при манипуляциях в 3D.
Я не хотел вас обидеть: есть статья, есть критика, в чем проблема?
Нынешняя объективная реальность такова, что если вы начинаете говорить об алгоритме, то вы должны представлять, что такое вычислительная сложность, именно на это я вам и указал, со всем уважением.
Опять переход в 3D. Большинство эффективных алгоритмов триангуляции Делоне на плоскости работают в плоскости. См. комментарий выше.
Нынешняя объективная реальность такова, что если вы начинаете говорить об алгоритме, то вы должны представлять, что такое вычислительная сложность, именно на это я вам и указал, со всем уважением.
Опять переход в 3D. Большинство эффективных алгоритмов триангуляции Делоне на плоскости работают в плоскости. См. комментарий выше.
<<Просто предлагать оптимизации к кубическому алгоритму для решения задачи при условии, что она решается за O(N log N) так же странно, как, например, пытаться где-то экономить копейки при регулярных бессмысленных милионных тратах>>
Согласен, конечно. Возможно приведенный пример и показывает то как не надо делать. И выводы каждый делает для себя свои. Но зато есть от чего оттолкнуться «новичкам». Я и сам «новичок» очень много полезного узнал из комментариев. Не написал бы, быть может и остался бы таким же «не образованным» как раньше.
А вообще из названия статьи следует, что рассказать я все таки хотел не сколько об сопутствующем алгоритме, а об оптимизации одного из его этапов, очень часто встречающихся не только в трассировке.
Согласен, конечно. Возможно приведенный пример и показывает то как не надо делать. И выводы каждый делает для себя свои. Но зато есть от чего оттолкнуться «новичкам». Я и сам «новичок» очень много полезного узнал из комментариев. Не написал бы, быть может и остался бы таким же «не образованным» как раньше.
А вообще из названия статьи следует, что рассказать я все таки хотел не сколько об сопутствующем алгоритме, а об оптимизации одного из его этапов, очень часто встречающихся не только в трассировке.
А рекламируемая книга настолько ли прекрасна, чтобы в ней можно было найти алгоритмы для более чем двумерных пространств?
Конечно не на столько. Она только повод чтобы перейти к 3D.
у меня вот какраз на переход к 3d тяму нехватает.
ориентация тетрэдров, векторные площади и объёмы, вот это всё.
ориентация тетрэдров, векторные площади и объёмы, вот это всё.
А в чем проблема с 3D? Считаем выпуклую оболочку точек на 4-мерном парабалоиде, и тетрангуляция в кармане.
Проблема какраз в выпуклой оболочке :)
Единственное «описание» такого алгоритма я нашёл в упомянутом комментом ниже cgal.
Но оно там на c++.
Единственное «описание» такого алгоритма я нашёл в упомянутом комментом ниже cgal.
Но оно там на c++.
Первая мысль — храним оболочку как двунаправленный граф тетраэдров (каждая вершина графа содержит номера соседних тетраэдров и индексы соответствующих граней в этих тетраэдрах — для удобства редактирования). Хотим добавить точку. Как-то находим любой видимый тетраэдр (видимость — знак некоторого определителя 4х4, ее даже понимать не надо). Выбрасываем тетраэдр, заменяем его на 4 (с 4-й вершиной в нашей точке), запоминаем все грани нового тетраэдра (как пары тетраэдр/индекс), в очереди. Потом в цикле «пока очередь не пуста» — берем грань, смотрим, с каким тетраэдром она граничит, проверяем видимость этого тетраэдра. Если видимый — заменяем 2 тетраэдра на 3, а внешние грани кладем в очередь.
Исходные точки лежали на строго выпуклой поверхности — значит, вершины из выпуклой оболочки пропадать не будут. И ситуации, когда мы обнаружили новый видимый тетраэдр, а отрезок соединяющий нашу точку с его дальней вершиной не пересекается с ближней гранью, тоже возникнуть не может (это аналог ситуации «невыпуклого 4-угольника» в двумерной триангуляции). Поэтому алгоритм получается проще, чем выпуклая оболочка в общем случае. Проблемы будут либо в старте, либо в в поиске «любого видимого тетраэдра». Можно отсортировать точки по x (тогда один из тетраэдров, содержащих две последние точки, будет видимым), но надо начитнать с невырожденного тетраэдра — а он не обязательно порождается первыми 4 точками.
Где-то я для своего 4D вьюера такую задачу решал. Интересно будет посмотреть, что там за алгоритм, а потом сравнить все три — старый, тот, который я сейчас описал, и описанный в cgal.
Исходные точки лежали на строго выпуклой поверхности — значит, вершины из выпуклой оболочки пропадать не будут. И ситуации, когда мы обнаружили новый видимый тетраэдр, а отрезок соединяющий нашу точку с его дальней вершиной не пересекается с ближней гранью, тоже возникнуть не может (это аналог ситуации «невыпуклого 4-угольника» в двумерной триангуляции). Поэтому алгоритм получается проще, чем выпуклая оболочка в общем случае. Проблемы будут либо в старте, либо в в поиске «любого видимого тетраэдра». Можно отсортировать точки по x (тогда один из тетраэдров, содержащих две последние точки, будет видимым), но надо начитнать с невырожденного тетраэдра — а он не обязательно порождается первыми 4 точками.
Где-то я для своего 4D вьюера такую задачу решал. Интересно будет посмотреть, что там за алгоритм, а потом сравнить все три — старый, тот, который я сейчас описал, и описанный в cgal.
Не стоит делать то, что уже хорошо сделано другими, как мне кажется. Посмотрите сюда. Там же, при желании, вы найдете и ссылки на соответствующие статьи.
Некорректно выразился. Делать-то, конечно, стоит, но для начала лучше попользоваться тем, что есть :)
Думаю, что наоборот. Стоит сначала попробовать сделать, а потом разобраться, как делали другие. Иначе это напоминает заглядывание в ответ задачника вместо решения задачи. Хотя, конечно, зависит от цели. Если надо, чтобы работало — а остальное (включая поддержку чужого алгоритма в своем коде) неважно, то можно и брать как есть.
cgal, разумеется, видел.
Cсылок на использованную литературу там полно, хотя где искать такую литературу не совсем понятно.
Чтение исходников для dD convex hull не осилил.
Cсылок на использованную литературу там полно, хотя где искать такую литературу не совсем понятно.
Чтение исходников для dD convex hull не осилил.
У гугла есть сервис для поиска статей: scholar.google.com. Большинство статей, опубликованных в руководстве пользователя CGAL, ищутся сразу.
А зачем вы читали исходники для convex hull, если в CGAL сразу дана реализация инкрементальной триангуляции? Если вы хотите реализовать самостоятельно статический алгоритм, то проще всего построить выпуклую оболочку точек в четырехмерном пространстве QuickHull'ом. Простой для понимания и для реализации алгоритм, используется повсеместно в статических случаях.
А зачем вы читали исходники для convex hull, если в CGAL сразу дана реализация инкрементальной триангуляции? Если вы хотите реализовать самостоятельно статический алгоритм, то проще всего построить выпуклую оболочку точек в четырехмерном пространстве QuickHull'ом. Простой для понимания и для реализации алгоритм, используется повсеместно в статических случаях.
quickhull хорошо и везде описан для 2d случая.
применение его для 4d вызывает затруднения в понимании
ориентации тетрэдров, векторных площадей и объёмов, вот это всё.
применение его для 4d вызывает затруднения в понимании
ориентации тетрэдров, векторных площадей и объёмов, вот это всё.
Вот статья вам в помощь. Кстати, ищется через scholar.google.com по ключевому слову quickhull.
В QuickHull прелагают для каждой новой грани выпуклой оболочки хранить уравнение гиперплоскости, ее содержащей. В случае 2D триангуляции это означает, что мы считаем плоскость, проходящую через (x1,y1,x1^2+y1^2), (x2,y2,x2^2+y2^2), (x3,y3,x3^2+y3^2), и потом за три умножения проверяем, нужно ли для вновь созданного соседнего треугольника делать флип. Интересно, даст ли это выигрыш в сложности (в константе, естественно).
Вычисление плоскости — 15 умножений на треугольник. Или 9 умножений на треугольник плюс предварительно 2 на каждую точку множества.
Вычисление плоскости — 15 умножений на треугольник. Или 9 умножений на треугольник плюс предварительно 2 на каждую точку множества.
Извините, а зачем 2 «порта»? Почему одного не достаточно?
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Оптимизация алгоритма проверки условия Делоне через уравнение описанной окружности и его применение