Недавно была статья о крутой картографической головоломке от Google. После того, как я потратил около 20 минут на разгадывание, захотелось понять можно ли сделать это автоматически?
Первое, что нужно сделать — это получить все полигоны. Почитав исходный код страницы и открыв консоль разработчика, родился такой код:
В массиве
Здесь была использована замечательная библиотека shapely, которая позволяет работать работать с гео-объектами прямо в питоне. Дальше мне подумалось о том, что вообщем зачем тогда цепляться к базе, если все так круто. Но вывод был плох — кроме как сериализовать объекты эта библиотека мне не подошла. Первая разница, которая бросилась в глаза — различные центроиды с постгисом в случаях, когда полигонов более одного. А поскольку я собирался сравнивать площади стран, то алгоритм был бы таков:
И алгоритм именно такой лишь потому, что shapely не умеет считать площадь географических объектов( по крайней мере я не нашел как). Поэтому все таки решил оставить привязку к postgis, потому что там можно преобразовывать геометрии в географию.
Ну а дальше все проще: нужно найти в интернете shape файл с полигонами стран, залить его в postgis и провести сравнения.
Шейпы я брал отсюда. Как загрузить их в базу написано много, проблемы могут быть только в кодировке, которая не UTF-8.
Осталась самая простая часть: сравнить площади
Я поставил
Вот что получилось:
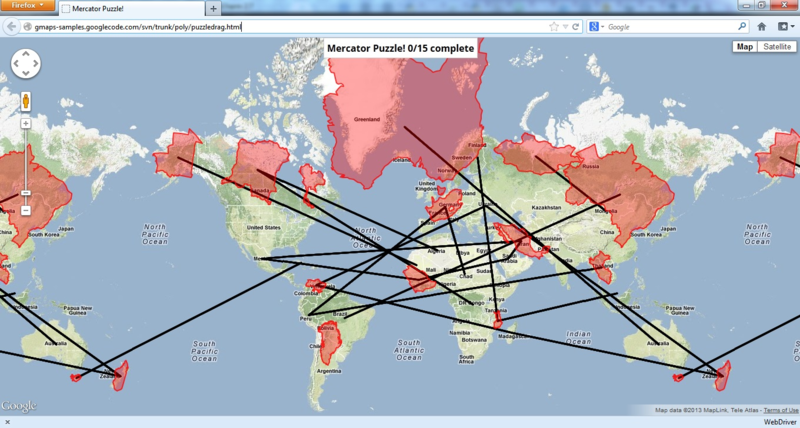
Чего не получилось: Гренландия, ЮАР, Исландия, Таиланд. Используя другой шейп, найденный у себя на диске, удалось добиться при тех же 2%, что не определились только ЮАР и Таиланд.
Из всего вышеизложенного следует вывод, что у меня не получилось, в следствии того, что я не знаю по каким данным гугл строит границы государств, а так же не известно как сильно они эти границы упростили.
Как я думаю, можно было бы добиться результата: добавить проверку подобия формы полигона. Но базовыми методами того же Postgis нельзя такое сделать. Алгоритм думаю таков: сильное упрощение геометрии, а затем сравнение углов в допустимом диапазоне.
Первое, что нужно сделать — это получить все полигоны. Почитав исходный код страницы и открыв консоль разработчика, родился такой код:
for (polyIdx=0;i<polys.length;polyIdx++){
var paths = polys[polyIdx].getPaths().getArray();
var arMultiPolygons=[];
for (j=0;j<paths.length;j++){
var arPolygons=[];
for (i=0;i<paths[j].length;i++) {
arPolygons.push([paths[j].getArray()[i].lng(),paths[j].getArray()[i].lat()]);
}
arMultiPolygons.push(p)
}
}
В массиве
polys — хранятся все полигоны. Дальше просто — получить координаты всех вершин полигонов, но при этом нужно не забыть, что все таки это МультиПолигоны. Дальше нужно эти полигоны положить в базу. Решение: selenium, который позволяет выполнять js-код. База — PostgreSQL + Postgis. from selenium import webdriver
from shapely.geometry import polygon,multipolygon
from shapely.wkt import loads
import psycopg2
con = psycopg2.connect(database="WB",user='postgres',password='pass', host='127.0.0.1', port='5432')
cur = con.cursor()
#Создание таблицы
сur.execute("create table googlePolygons ( idx integer, googlegeom geometry );")
browser = webdriver.Firefox()
browser.get("http://gmaps-samples.googlecode.com/svn/trunk/poly/puzzledrag.html")
polysCount = browser.execute_script('return polys.length;')
for iPoly in xrange(polysCount):
element = browser.execute_script('var paths = polys[%s].getPaths().getArray();var arMultiPolygons=[];'
'for (j=0;j<paths.length;j++){ var arPolygons=[];'
'for (i=0;i<paths[j].length;i++) '
'{arPolygons.push([paths[j].getArray()[i].lng(),paths[j].getArray()[i].lat()]);} arMultiPolygons.push(p)}'
'return arMultiPolygons;'% str(iPoly))
polygons = []
#Делаем массив из полигонов
for i in element: polygons.append(polygon.Polygon(i))
#Записываем уже мультиполигон
cur.execute("insert into googlePolygons (googlegeom,idx) values (geomfromewkt('"+multipolygon.MultiPolygon(polygons).wkt+"')," + str(iPoly)+");")
con.commit()
Здесь была использована замечательная библиотека shapely, которая позволяет работать работать с гео-объектами прямо в питоне. Дальше мне подумалось о том, что вообщем зачем тогда цепляться к базе, если все так круто. Но вывод был плох — кроме как сериализовать объекты эта библиотека мне не подошла. Первая разница, которая бросилась в глаза — различные центроиды с постгисом в случаях, когда полигонов более одного. А поскольку я собирался сравнивать площади стран, то алгоритм был бы таков:
- Брался полигон, из него вычитался центроид, дальше добавлялся бы центроид страны, с которой проводилась сверка (иначе говоря — двигал полигон)
- Дальше считалось бы отношение, на которое нужно приблизить\отдалить каждую точку на границе полигона от центроида (увеличение\уменьшение масштаба из-за проекции)
- Считалась площадь
И алгоритм именно такой лишь потому, что shapely не умеет считать площадь географических объектов( по крайней мере я не нашел как). Поэтому все таки решил оставить привязку к postgis, потому что там можно преобразовывать геометрии в географию.
Ну а дальше все проще: нужно найти в интернете shape файл с полигонами стран, залить его в postgis и провести сравнения.
Шейпы я брал отсюда. Как загрузить их в базу написано много, проблемы могут быть только в кодировке, которая не UTF-8.
Осталась самая простая часть: сравнить площади
cur.execute("select idx,st_area(geography(st_setsrid(googlegeom,4326)))/1000000, "
"st_astext(st_centroid(st_setsrid(googlegeom,4326))) "
"from googlePolygons order by idx;")
unRealC = cur.fetchall()
cur.execute("select name, st_area(geography(st_setsrid(geom,4326)))/1000000, "
"st_astext(st_centroid(st_setsrid(geom,4326))) from tm_world_borders;")
realC = cur.fetchall()
for urc in unRealC:
for rc in realC:
if float(abs(rc[1]-urc[1])) /rc[1]<0.02:
browser.execute_script('pl = new google.maps.Polyline('
'{path: [new google.maps.LatLng('+str(loads(rc[2]).y)+','+ str(loads(rc[2]).x)+'),'
' new google.maps.LatLng('+str(loads(urc[2]).y)+','+ str(loads(urc[2]).x)+')],'
'map: map});')
Я поставил
float(abs(rc[1]-urc[1])) /rc[1]<0.02 — 2% ошибки. Добавил линию, которая соединяла цент исходного полигона с центром вероятного действительного его расположения. loads() — преобразование WKT в объект.Вот что получилось:

Чего не получилось: Гренландия, ЮАР, Исландия, Таиланд. Используя другой шейп, найденный у себя на диске, удалось добиться при тех же 2%, что не определились только ЮАР и Таиланд.
Из всего вышеизложенного следует вывод, что у меня не получилось, в следствии того, что я не знаю по каким данным гугл строит границы государств, а так же не известно как сильно они эти границы упростили.
Как я думаю, можно было бы добиться результата: добавить проверку подобия формы полигона. Но базовыми методами того же Postgis нельзя такое сделать. Алгоритм думаю таков: сильное упрощение геометрии, а затем сравнение углов в допустимом диапазоне.






