Комментарии 18
«Вроде как, английский язык придумали у вас, а говорите все так, что ничего понять невозможно» (LOCK, STOCK AND TWO SMOKING BARRELS)
Вот и я вижу Python, знаю Python и ничего не понятно. Но интересно.
Вот и я вижу Python, знаю Python и ничего не понятно. Но интересно.
+4
Хм… Честно говоря, я надеялся написать пост, который был бы понятен даже людям, не знающим Python. А что именно не понятно?
0
… который был бы понятен даже людям, не знающим Python...
А как насчет людей не знающих математики? ))
«Я сожалею, но в вашей системе спиртообращения все еще есть немного крови» (с)
Просто специфика, мат анализа в коде больше чем кода. Это не плохо и не хорошо, это факт. Как и то, что в посте python используется для специфической (с моей точки зрения) задачи в области от которой я очень далек. Это похоже на татарский язык, 99% букв «русские» — но слова из них собираются не правильные! И для меня это выглядит так:
from mbook import magic
result = magic.do()
print result
0
Так, собственно, для этого я написал первый пост, в котором нет ничего, кроме математики. Вот ссылка.
На самом деле я взялся за, наверное, довольно сложную задачу — рассказать про методы наиболее понятным языком для наиболее широкой аудитории. Что-то вроде популяризации. Поэтому, если у вас есть какие-то конкретные комментарии, я был бы им очень рад. Тогда я мог бы или подкорректировать эти два поста, или написать еще один.
На самом деле я взялся за, наверное, довольно сложную задачу — рассказать про методы наиболее понятным языком для наиболее широкой аудитории. Что-то вроде популяризации. Поэтому, если у вас есть какие-то конкретные комментарии, я был бы им очень рад. Тогда я мог бы или подкорректировать эти два поста, или написать еще один.
+1
Я смотрю код и не понимаю, где там Байес. Можно поподробней это момент?
0
Честно говоря, я не очень понимаю вопрос «где там Байес».
Если говорить только о логике программы, то на последнем рисунке вы видите архитектуру модели.
В файле model.py имплементируется эта архитектура, то есть описываются все узлы и связи между ними, задаются все распределения.
В файле run_model.py самыми выжными являются две строчки:
Первая определяет, что надо использовать алгоритм MCMC для нашей модели, а вторая делает выборку в соостветствии с этим алгоритмом.
Обрабатывая выборку, мы получается наиболее вероятные значения, погрешности, среднии и пр.
Математика сидит в архитектуре модели. То есть у вас есть формула Байеса, в которой есть функция правдоподобия, зависящая от параметров, и априорные распределения параметров. Эта структура формулы Байеса и есть архитектура модели.
В общем случае формула Байеса может быть усложнена, то есть у вас может быть функция правдоподобия, зависящая от параметров, априорные распределения параметров, зависящие от других параметров, а потом априорные распределения этих самых других параметров. Все это описывается архитектурой модели.
Если говорить только о логике программы, то на последнем рисунке вы видите архитектуру модели.
В файле model.py имплементируется эта архитектура, то есть описываются все узлы и связи между ними, задаются все распределения.
В файле run_model.py самыми выжными являются две строчки:
D = pymc.MCMC(model, db = 'pickle')
D.sample(iter = 10000, burn = 1000)
Первая определяет, что надо использовать алгоритм MCMC для нашей модели, а вторая делает выборку в соостветствии с этим алгоритмом.
Обрабатывая выборку, мы получается наиболее вероятные значения, погрешности, среднии и пр.
Математика сидит в архитектуре модели. То есть у вас есть формула Байеса, в которой есть функция правдоподобия, зависящая от параметров, и априорные распределения параметров. Эта структура формулы Байеса и есть архитектура модели.
В общем случае формула Байеса может быть усложнена, то есть у вас может быть функция правдоподобия, зависящая от параметров, априорные распределения параметров, зависящие от других параметров, а потом априорные распределения этих самых других параметров. Все это описывается архитектурой модели.
0
Я еще не совсем понимаю базовые вещи, поэтому задаю вопросы в стиле Кэпа.
Вот как я понимаю задачу: есть некий процесс, который можно выразить через формулу y=ax+b, мы проводим серию измерений, но в результатах видим шум. Наша задача — выяснить эти a и b.
Теорема Байеса позволяет оценить вероятность значения параметра, зная конечные данные. И вот тут начинаются вопросы. Предыдущую статью читал 3 раза, все равно не ясно.
Конечная формула:
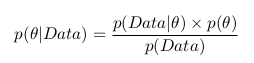
Я так понимаю, решение состоит в том, чтобы перебрать все возможные значения параметра, и выбрать значение с максимальной вероятностью.
Но каким образом считаются части формулы?
p(Data|θ)=1, т.к. всегда при заданных a, b и шуме, получим одно и то же значение?
Как посчитать p(θ)=p(a,b, шум)? Интуиция говорит, если мы перебираем все возможные значения, то это константа и она равна 1/(общее количество перебраных значений) — это так?
Почему делается вывод, что p(Data) — это константа? Если добавляется шум, разве не может быть так, что некие значения встречаются чаще, чем другие? Смотрел в Вики определение «гауссова шума», судя по определению, в центре «пика» значения встречаются чаще, чем по бокам. Это если я правильно понимаю, что Data — это какое-либо значение, ну например если Data=3, то p(Data=3) это вероятность того, что встретится тройка = количество троек в результате / общее количество данных.
Я все никак не могу ухватить суть, понять на интуитивном уровне, поэтому такие вопросы. Высшая математика была сдана на отлично и успешно забыта 10 лет назад.
Вот как я понимаю задачу: есть некий процесс, который можно выразить через формулу y=ax+b, мы проводим серию измерений, но в результатах видим шум. Наша задача — выяснить эти a и b.
Теорема Байеса позволяет оценить вероятность значения параметра, зная конечные данные. И вот тут начинаются вопросы. Предыдущую статью читал 3 раза, все равно не ясно.
Конечная формула:

Я так понимаю, решение состоит в том, чтобы перебрать все возможные значения параметра, и выбрать значение с максимальной вероятностью.
Но каким образом считаются части формулы?
p(Data|θ)=1, т.к. всегда при заданных a, b и шуме, получим одно и то же значение?
Как посчитать p(θ)=p(a,b, шум)? Интуиция говорит, если мы перебираем все возможные значения, то это константа и она равна 1/(общее количество перебраных значений) — это так?
Почему делается вывод, что p(Data) — это константа? Если добавляется шум, разве не может быть так, что некие значения встречаются чаще, чем другие? Смотрел в Вики определение «гауссова шума», судя по определению, в центре «пика» значения встречаются чаще, чем по бокам. Это если я правильно понимаю, что Data — это какое-либо значение, ну например если Data=3, то p(Data=3) это вероятность того, что встретится тройка = количество троек в результате / общее количество данных.
Я все никак не могу ухватить суть, понять на интуитивном уровне, поэтому такие вопросы. Высшая математика была сдана на отлично и успешно забыта 10 лет назад.
0
Вы правильно понимаете задачу и правильно написали конечную формулу, далее начинается небольшая путаница.
θ — это параметр. В нашем случае, у нас есть два параметры, которые не зависят друг от друга: a и b (шум — это не параметр, это просто отклонение a и b от своих средних значений), поэтому для нашего случая мы можем переписать формулу в следующем виде:
p(a,b|Data) = p(Data|a,b)*p(a)*p(b) / p(Data)
p(θ) = p(a)*p(b) — это наше априорное распределение, которое мы задаем. То есть мы задает p(a) и p(b).
Data — это наши экспериментальные данные (набор точек {x_i,y_i}). Они нам даны изначально и не зависят от параметров, и не изменяются с изменением параметров. То есть для нашей задачи они являются константой, поэтому p(Data) тоже является константой (это более интуитивное объяснение постоянности p(Data)).
Если объяснять «на пальцах», то наша задача заключается в следующем:
У нас есть прямая y = a*x + b. Если мы возьмем отдельную точку этой прямой (x=0.2, например), то из-за присутствия шума y может принимать для этой точки любые значения вокруг нашей прямой, то есть они распределены нормально со средним a*0.2 + b и дисперсией \sigma (которую мы предполагаем известной — дисперсия шума). И так случилось, что наш эксперимент дал нам в этой точке значение y, например, равное 0.5. Это значит, что при данных a и b (которые определяют среднее распределения) мы можем посчитать вероятность получить то значение y, которое мы получили экспериментально. Как вы видите, из формы нормального распределения следует, что наибольшая вероятность будет у значений, равных среднему, то есть равных a*0.2 + b (т.е. лежащих на прямой y=a*x+b). Чем дальше значение y от среднего (от прямой), тем меньше у него вероятность. Так происходит во всех точках. Наша задача в том, чтобы найти такие коэффициенты a и b, чтобы все экспериментальные точки лежали наиболее близко к прямой (то есть, чтобы их совокупная вероятность была наибольшей).
θ — это параметр. В нашем случае, у нас есть два параметры, которые не зависят друг от друга: a и b (шум — это не параметр, это просто отклонение a и b от своих средних значений), поэтому для нашего случая мы можем переписать формулу в следующем виде:
p(a,b|Data) = p(Data|a,b)*p(a)*p(b) / p(Data)
p(θ) = p(a)*p(b) — это наше априорное распределение, которое мы задаем. То есть мы задает p(a) и p(b).
Data — это наши экспериментальные данные (набор точек {x_i,y_i}). Они нам даны изначально и не зависят от параметров, и не изменяются с изменением параметров. То есть для нашей задачи они являются константой, поэтому p(Data) тоже является константой (это более интуитивное объяснение постоянности p(Data)).
Если объяснять «на пальцах», то наша задача заключается в следующем:
У нас есть прямая y = a*x + b. Если мы возьмем отдельную точку этой прямой (x=0.2, например), то из-за присутствия шума y может принимать для этой точки любые значения вокруг нашей прямой, то есть они распределены нормально со средним a*0.2 + b и дисперсией \sigma (которую мы предполагаем известной — дисперсия шума). И так случилось, что наш эксперимент дал нам в этой точке значение y, например, равное 0.5. Это значит, что при данных a и b (которые определяют среднее распределения) мы можем посчитать вероятность получить то значение y, которое мы получили экспериментально. Как вы видите, из формы нормального распределения следует, что наибольшая вероятность будет у значений, равных среднему, то есть равных a*0.2 + b (т.е. лежащих на прямой y=a*x+b). Чем дальше значение y от среднего (от прямой), тем меньше у него вероятность. Так происходит во всех точках. Наша задача в том, чтобы найти такие коэффициенты a и b, чтобы все экспериментальные точки лежали наиболее близко к прямой (то есть, чтобы их совокупная вероятность была наибольшей).
+1
мы задаем p(a) и p(b)
как именно? a и b — это числа, так? В коде у вас есть кусок a = pymc.Uniform('a', 0., 20.), это значит, что a может принимать значения от 0 до 20? Значит, вероятность получить, например, 5 равна 1/(общее количество «a»)?
Data — это наши экспериментальные данные (набор точек {x_i,y_i})
Ааа, так это массив из пар чисел, а не из одного числа. Я подумал про одномерный массив, т.к. у вас в коде data = true_coefficients[0]*x + true_coefficients[1] + noise
Тогда p(Data) — это вероятность появления пары xi,yi в конечных данных? Тогда оно равно 1/(общее количество пар данных), так?
0
Вероятность получить какое-либо значение зависит от распределения.
Если у нас равномерное распределение (как в случае с a), то у нас одинаковая вероятность получить любое значение из отрезка, на котором определено это распределение. То есть в случае a = pymc.Uniform('a', 0., 20.) вероятность получить любое значение a (в том числе 5) одинакова и равна 1/(20-0), то есть 1/(верхняя_граница — нижняя_граница).
В случае с Data, мы говорим, что данные распределены нормально вокруг прямой y=a*x+b, поэтому вероятность получить любое значение рассчитывается по формуле для нормального распределение со средним, равным a*x+b, и дисперсией, равной \sigma. Эта вероятность пропорциональна величине ( (y_i — a*x_i — b) / (\sigma) )^2
Если у нас равномерное распределение (как в случае с a), то у нас одинаковая вероятность получить любое значение из отрезка, на котором определено это распределение. То есть в случае a = pymc.Uniform('a', 0., 20.) вероятность получить любое значение a (в том числе 5) одинакова и равна 1/(20-0), то есть 1/(верхняя_граница — нижняя_граница).
В случае с Data, мы говорим, что данные распределены нормально вокруг прямой y=a*x+b, поэтому вероятность получить любое значение рассчитывается по формуле для нормального распределение со средним, равным a*x+b, и дисперсией, равной \sigma. Эта вероятность пропорциональна величине ( (y_i — a*x_i — b) / (\sigma) )^2
0
А есть ли идеи, почему результаты МНК не совпали с байесовскими? Ведь в прошлый раз уже доказали, что при нормальном шуме с постоянной дисперсией это одно и то же?
0
Мой ответ: в вероятностном характере байесовских методов. Здесь есть два аспекта. Во-первых, невозможно сгенерировать две одинаковые выборки, и, соответственно, их среднее будет каждый раз отличаться. Во-вторых, есть погрешность в вычислении наиболее вероятного значения. Потому что его расчет зависит от того, какая сетка для гистограммы выбрана (если сетка слишком мелкая, то за наиболее вероятное можно по ошибке принять случайный выброс, а если слишком грубая, то тогда усреднение будет проводиться по слишком большому количеству значений.
0
Так ведь и МНК, и байес вычисляют результат не точно. У МНК есть вполне просто вычисляемая статистическая погрешность — можно использовать стандартное отклонение. У байеса, наверное, тоже можно в каком-то виде погрешность определить. Кстати, интересно, в каком?
В целом спасибо большое за статьи, очень понятное введение для такой неинтуитивной темы!
0
А у вас нет желания оформить этот, туториал, явно расчитанный на аудиторию занимающуюся исследованиями, в виде IPython notebook? Уже есть впечатляющая коллекция подобных ноутбуков c «академическими» примерами рассчётов в Python:
github.com/ipython/ipython/wiki/A-gallery-of-interesting-IPython-Notebooks
github.com/ipython/ipython/wiki/A-gallery-of-interesting-IPython-Notebooks
+1
Честно говоря, я не очень уверен, что подобная статья будет интересна англоязычной аудитории, потому что там довольно много подобных материалов. Вот, например, на указанном вами сайте я сразу же нашел туториал по байесовким методам. С одной стороны, он менее подробно описан, но с другой стороны, конкретно этот пример я видел в нескольких англоязычных книжках, где описание достаточно полное. Я пишу англоязычные научные статьи, и этого мне вполне достаточно. А писать подобные посты о байесовских методах на русском — это просто хобби. Да и к тому же это хорошее развитие собственных педагогических способностей.
0
Ноутбук прекрасно работает с русским, например nbviewer.ipython.org/4964582. Русскоязычной аудитории было бы тоже интересно ваш код прямо из статьи запускать, а не копипастить )
0
Промахнулся
0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Байесовский анализ в Python