Ну, мы продолжаем. Перейдём уже ближе к тому, чем внешне вполне завлекательна гидродинамика, и постараемся добавить как можно больше красивых и условно красивых картинок.
В тексте будет написано ещё немножечко теории на примере задачи об устойчивости течения в плоском канале. Таких задач в реальности великое множество — в слоях и в ограниченных полостях разной формы, в слоях вертикальных, горизонтальных и наклонных, в обычной жидкости и пористой среде, в проводящей жидкости под влиянием магнитного поля и в растворе какой-нибудь соли под действием температуры, в полости под влиянием как угодно направленной вибрации, на границе раздела двух жидкостей… В общем, одно только перечисление всех подуровней гидродинамики может отнять пару часов, и то всё вспомнить вряд ли удастся. А также будет показано несколько примеров чисто гидродинамической неустойчивости течений, без влияния дополнительных факторов (изображения около 700 кбайт).
Предыдущие же посты были написаны, чтобы обеспечить математический и смысловой фундамент формул в дальнейших постах.
Кратко о гидродинамике: ты помнишь, как всё начиналось?
Кратко о гидродинамике: уравнения движения
Кратко о гидродинамике: сохранение энергии
Теория устойчивости вообще — весьма широкая область, которую можно встретить и в теоретической механике, и в теориях линейных и нелинейных колебаний (где она наиболее развита). Особнячком в ней держится теория гидродинамической устойчивости, в силу специфики изучаемого объекта и соответствующих ему систем уравнений. Рассмотрим пару простейших (и наиболее, пожалуй, фундаментальных) примеров.
Пусть у нас некоторое произвольное течение несжимаемой вязкой жидкости. Вполне естественно, что оно описывается уравнениями Навье-Стокса:
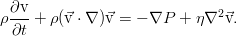
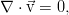
Уравнения приведены пока ещё в размерной форме. Но их удобно обезразмерить для дальнейшей работы, т.к. эта операция сокращает число параметров и сразу позволяет установить, какие же механизмы наиболее существенны в поведении системы. Процедура обезразмеривания сводится к перемасштабированию всех переменных таким образом, чтобы минимизировать число параметров. Чаще всего определяющим оказывается масштаб времени — мы можем выбрать в качестве его единицы характерное время, за которое поток со своей характерной скоростью пройдёт какую-то характерную длину канала (для краткости назовём его кинематическим, т.к. оно определяется школьным соотношением время = расстояние / скорость, но такого термина нигде не встречается), время переноса импульса (вязкое время), тепла (тепловое время), внешнего воздействия и т.п. Для уравнений движения в канале наиболее удобно взять кинематические времена, указать некоторый условный масштаб скорости, длины, а масштаб для давления выберем, исходя из наибольшего упрощения уравнения:
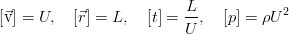
При подстановке масштабов в уравнение и сокращении на плотность и множитель перед нелинейным слагаемым мы увидим, что все коэффициенты становятся равны единичкам, за исключением вязкого слагаемого. Там возникает комбинация параметров, выражающая обратное число Рейнольдса:
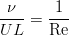
Второе уравнение своего вида при обезразмеривании не изменит. Таким образом, число Рейнольдса оказывается единственным параметром, определяющим поведение системы.
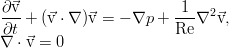
Шик в том, что только этот один параметр отвечает за ламинарность или турбулентность течения, уравнения же при этом не меняются ни капельки.
Допустим далее, что у нас есть некоторый стационарный, неизменный во времени поток со скоростью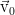 , и есть некоторые бесконечно малые возмущения этого потока:
, и есть некоторые бесконечно малые возмущения этого потока:

Можно благополучно подставить в систему скорость и давление в такой форме, отбросить всё, что содержит только стационарные поля скорости и давления, т.к. они удовлетворяют уравнениям сами по себе, и пренебречь нелинейным слагаемым — это самый важный ход во всей теории. Т.к. мы полагаем возмущения бесконечно малыми, то слагаемое вида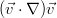 становится бесконечно малой второго порядка. Потому, говоря, что мы работаем в области, где возмущения ещё можно считать малыми (т.е. в самом-самом начале развития будущих неустойчивостей), можем смело отбросить нелинейность. В итоге остаются два линейных уравнения, хотя и с переменными коэффициентами:
становится бесконечно малой второго порядка. Потому, говоря, что мы работаем в области, где возмущения ещё можно считать малыми (т.е. в самом-самом начале развития будущих неустойчивостей), можем смело отбросить нелинейность. В итоге остаются два линейных уравнения, хотя и с переменными коэффициентами:
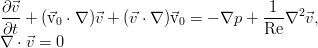
Эта система является основной системой уравнений линейной теории гидродинамической устойчивости, и описывает самые общие ситуации. Посмотрим теперь на одну более специфичную ситуацию — устойчивость плоскопараллельного течения в некотором канале. Всё происходит в плоскости (x, z), а вдоль оси y канал — бесконечно протяжённый — то есть, чисто двумерное течение. Пусть стационарное решение имеет только одну компоненту, зависящую от поперечной координаты канала, а возмущения — две компоненты:
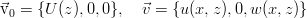
Также примем (поскольку уравнения линейные и типичным решением для них является экспонента) экспоненциальную зависимость от времени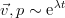 . Такие возмущения принято называть «нормальными», хотя история этого термина довольно туманна. Подставляя указанную зависимость и записывая уравнения в проекциях на оси, получим систему для плоских возмущений. При этом, коэффициенты в ней не зависят от координаты x, потому можно дополнотиельно принять, что возмущения периодичны вдоль этой оси — по сути, это близко к разложению в ряд Фурье и рассмотрению только одной компоненты:
. Такие возмущения принято называть «нормальными», хотя история этого термина довольно туманна. Подставляя указанную зависимость и записывая уравнения в проекциях на оси, получим систему для плоских возмущений. При этом, коэффициенты в ней не зависят от координаты x, потому можно дополнотиельно принять, что возмущения периодичны вдоль этой оси — по сути, это близко к разложению в ряд Фурье и рассмотрению только одной компоненты: 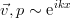 . Получается такая вот система, уже из обычных дифференциальных уравнений (штрихом обозначена производная по z):
. Получается такая вот система, уже из обычных дифференциальных уравнений (штрихом обозначена производная по z):
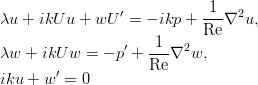
Опустив промежуточные преобразования, несложные, но занимающие пару страниц, укажем, что эту систему можно свести к одному уравнению для компоненты скорости w:
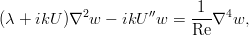
Если в нём записать комплексный инкремент и ввести фазовую скорость возмущений
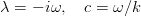
получится уравнение, известное под названием уравнения Орра-Зоммерфельда:
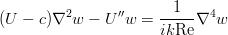
Вся линейная теория гидродинамической устойчивости течений базируется на этом уравнении. Правда, точных решений для него нет, независимо от вида стационарного течения и граничных условий, хотя внешне выглядит всё крайне просто и задача является замкнутой.
В решении этой задачи были разные подходы. Например, Рэлей в приближении больших чисей Рейнольдса просто пренебрёг правой частью. Конечно, это не всегда корректно, поскольку четвертые производные могут запросто компенсировать знаменатель. Правда, решить уравнение всё равно не получилось, зато получилось доказать теорему о необходимом условии устойчивости потока. Правда, для течения Пуазейля это условие не выполнено, но оно всё равно может быть неустойчивым.
Можно, в том же приближении, протянуть разложение по обратному числу Рейнольдса как малому параметру. В нулевом порядке данного разложения получится упомянутая задача Рэлея, а если пойти чуть дальше — можно поймать две кривые на плоскости параметров (k, Re), между которыми будет заключена область неустойчивости течения, в которой возмущения нарастают и приводят к разрушению стационарного профиля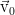 . Сперва эту проблему, для течения Пуазейля, пытался решить Гейзенберг (тот самый Вернер Гейзенберг, создатель матричной квантовой механики), но полностью довести разложение у него не получилось. В итоге, в 1944 году, за дело взялся терпеливый китаец Линь Цзя-Цзяо, протянул разложения чуть дальше и экстраполировал обе кривых, которые замкнулись в одну. Получилось у него примерно следующее (сплошная линия):
. Сперва эту проблему, для течения Пуазейля, пытался решить Гейзенберг (тот самый Вернер Гейзенберг, создатель матричной квантовой механики), но полностью довести разложение у него не получилось. В итоге, в 1944 году, за дело взялся терпеливый китаец Линь Цзя-Цзяо, протянул разложения чуть дальше и экстраполировал обе кривых, которые замкнулись в одну. Получилось у него примерно следующее (сплошная линия):
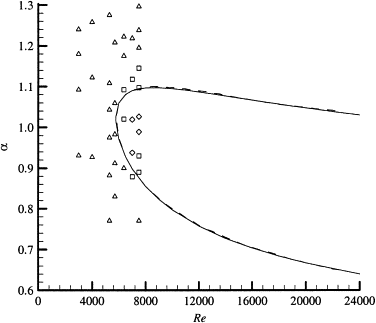
На самом деле, этот график уже немного для другой системы — вместо обычной жидкости у авторов рассматривалась суспензия некоторых волокон в канале, но смысл его тот же самый и существенных качественных отличий от теории Линя нет (иллюстрация из работы You Zhenjianga, Lin Jianzhonga, Yu Zhaoshengb. Hydrodynamic instability of fiber suspensions in channel flows. Fluid Dynamics Research, Volume 34 (4), 2004, pp. 251–271). В целом, течение Пуазейля практически для любой жидкости имеет такие свойства устойчивости, что только подчёркивает фундаментальность результатов Линя.
Ниже будут картинки, преимущественно надёрганные из «Альбома течений жидкости и газа» (М. Ван-Дайк) и просто из сети, с небольшими комментариями по конкретным постановкам задач.
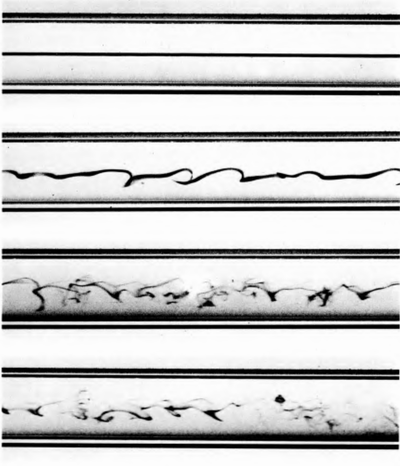
Этот эксперимент был проведён Рейнольдсом в 1883 г. Фотографии сделаны на той же установке, которая благополучно сохранилась, примерно сто лет спустя. Сверху вниз на фотографиях возрастает скорость течения. В поток вводится тонкая подкрашенная струйка, которая позволяет отлично визуализировать течение.
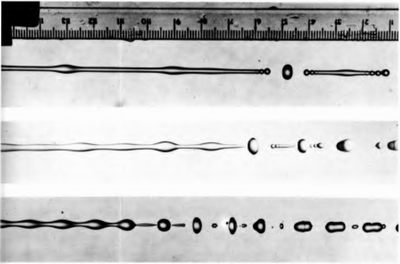
Весьма изящная неустойчивость, которую мы можем наблюдать каждый день. Достаточно открыть кран так, чтобы струйка была ровной и тонкой, но при этом достаточно длинной. За счёт взаимодействия случайных возмущений и капиллярных сил непрерывная струйка стремится разбиться на мелкие капли, т.к. это энергетически выгоднее. Здесь жидкость возмущается за счёт громкоговорителя, к которому присоединена выводящая трубка. Длина волны возмущения на нижней картинке близка к теоретическому критическому значению.
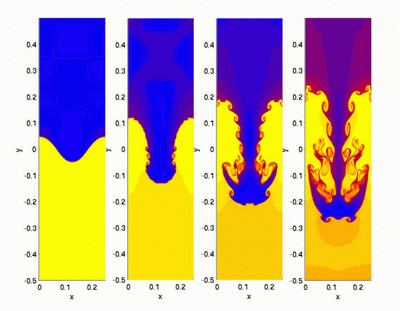


Довольно незамысловатая ситуация — на поверхность лёгкой жидкости мы наливаем тяжёлую. Вполне очевидно, что тяжёлая будет стремиться «провалиться» вниз, хотя до поры до времени процессу может противостоять поверхностное натяжение. Зато когда движение начинается, происходит это очень красиво, как в лабораториях и расчётах, так и в природе (вторая картинка перевёрнута, по задумке её автора-фотохудожника).

Аналогичное явление наблюдается, если в среде существуют две области с сильно различающимися давлениями — через границу раздела между ними вещество «продавливается» и порождает аналогичные простому «проваливанию» структуры.

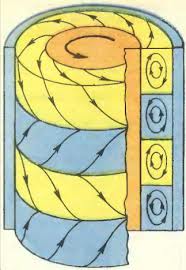
Ещё одна версия неустойчивости, чем-то по происхождению подобной рэлей-тейлоровской. Жидкость находится между двумя соосными цилиндрами и приводится в быстрое вращение. За счёт центростремительных ускорений в изначально неподвижной относительно стенок цилиндров среде формируются кольцевые ячейки с противоположными направлениями течения.
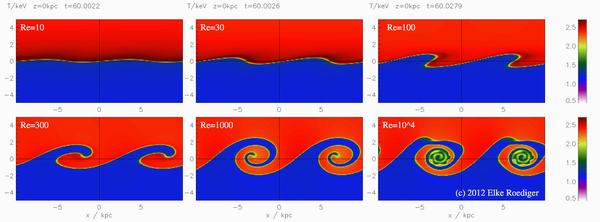


И ещё одна версия неустойчивости. Тоже, физически, весьма простая. У нас есть два потока несмешивающихся жидкостей, движущихся противоположно друг другу. Либо просто с разными скоростями — т.е. на границе раздела между ними существует скачок скорости, благодаря которому возмущения поверхности деформируются, закручиваются и порождают замысловатые вихорёчки, а потом и вовсе перемешивают жидкости. Так же интересно смотрится и в расчётах, и в экспериментальной установке, и в природе.
Здесь, конечно, показан далеко не весь спектр возможных неустойчивостей — область неисчерпаема, и содержит огромный спектр до сих пор неизученных явлений и их особенностей. Следующий пост будет о конвекции и соответствующих неустойчивостях, вызванных неоднородностью температуры в системе.
В тексте будет написано ещё немножечко теории на примере задачи об устойчивости течения в плоском канале. Таких задач в реальности великое множество — в слоях и в ограниченных полостях разной формы, в слоях вертикальных, горизонтальных и наклонных, в обычной жидкости и пористой среде, в проводящей жидкости под влиянием магнитного поля и в растворе какой-нибудь соли под действием температуры, в полости под влиянием как угодно направленной вибрации, на границе раздела двух жидкостей… В общем, одно только перечисление всех подуровней гидродинамики может отнять пару часов, и то всё вспомнить вряд ли удастся. А также будет показано несколько примеров чисто гидродинамической неустойчивости течений, без влияния дополнительных факторов (изображения около 700 кбайт).
Предыдущие же посты были написаны, чтобы обеспечить математический и смысловой фундамент формул в дальнейших постах.
Кратко о гидродинамике: ты помнишь, как всё начиналось?
Кратко о гидродинамике: уравнения движения
Кратко о гидродинамике: сохранение энергии
Теория устойчивости вообще — весьма широкая область, которую можно встретить и в теоретической механике, и в теориях линейных и нелинейных колебаний (где она наиболее развита). Особнячком в ней держится теория гидродинамической устойчивости, в силу специфики изучаемого объекта и соответствующих ему систем уравнений. Рассмотрим пару простейших (и наиболее, пожалуй, фундаментальных) примеров.
Устойчивость двумерного течения
Пусть у нас некоторое произвольное течение несжимаемой вязкой жидкости. Вполне естественно, что оно описывается уравнениями Навье-Стокса:
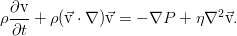
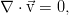
Уравнения приведены пока ещё в размерной форме. Но их удобно обезразмерить для дальнейшей работы, т.к. эта операция сокращает число параметров и сразу позволяет установить, какие же механизмы наиболее существенны в поведении системы. Процедура обезразмеривания сводится к перемасштабированию всех переменных таким образом, чтобы минимизировать число параметров. Чаще всего определяющим оказывается масштаб времени — мы можем выбрать в качестве его единицы характерное время, за которое поток со своей характерной скоростью пройдёт какую-то характерную длину канала (для краткости назовём его кинематическим, т.к. оно определяется школьным соотношением время = расстояние / скорость, но такого термина нигде не встречается), время переноса импульса (вязкое время), тепла (тепловое время), внешнего воздействия и т.п. Для уравнений движения в канале наиболее удобно взять кинематические времена, указать некоторый условный масштаб скорости, длины, а масштаб для давления выберем, исходя из наибольшего упрощения уравнения:

При подстановке масштабов в уравнение и сокращении на плотность и множитель перед нелинейным слагаемым мы увидим, что все коэффициенты становятся равны единичкам, за исключением вязкого слагаемого. Там возникает комбинация параметров, выражающая обратное число Рейнольдса:
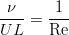
Второе уравнение своего вида при обезразмеривании не изменит. Таким образом, число Рейнольдса оказывается единственным параметром, определяющим поведение системы.

Шик в том, что только этот один параметр отвечает за ламинарность или турбулентность течения, уравнения же при этом не меняются ни капельки.
Допустим далее, что у нас есть некоторый стационарный, неизменный во времени поток со скоростью
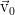 , и есть некоторые бесконечно малые возмущения этого потока:
, и есть некоторые бесконечно малые возмущения этого потока:
Можно благополучно подставить в систему скорость и давление в такой форме, отбросить всё, что содержит только стационарные поля скорости и давления, т.к. они удовлетворяют уравнениям сами по себе, и пренебречь нелинейным слагаемым — это самый важный ход во всей теории. Т.к. мы полагаем возмущения бесконечно малыми, то слагаемое вида
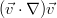 становится бесконечно малой второго порядка. Потому, говоря, что мы работаем в области, где возмущения ещё можно считать малыми (т.е. в самом-самом начале развития будущих неустойчивостей), можем смело отбросить нелинейность. В итоге остаются два линейных уравнения, хотя и с переменными коэффициентами:
становится бесконечно малой второго порядка. Потому, говоря, что мы работаем в области, где возмущения ещё можно считать малыми (т.е. в самом-самом начале развития будущих неустойчивостей), можем смело отбросить нелинейность. В итоге остаются два линейных уравнения, хотя и с переменными коэффициентами:
Эта система является основной системой уравнений линейной теории гидродинамической устойчивости, и описывает самые общие ситуации. Посмотрим теперь на одну более специфичную ситуацию — устойчивость плоскопараллельного течения в некотором канале. Всё происходит в плоскости (x, z), а вдоль оси y канал — бесконечно протяжённый — то есть, чисто двумерное течение. Пусть стационарное решение имеет только одну компоненту, зависящую от поперечной координаты канала, а возмущения — две компоненты:
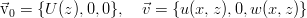
Также примем (поскольку уравнения линейные и типичным решением для них является экспонента) экспоненциальную зависимость от времени
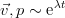 . Такие возмущения принято называть «нормальными», хотя история этого термина довольно туманна. Подставляя указанную зависимость и записывая уравнения в проекциях на оси, получим систему для плоских возмущений. При этом, коэффициенты в ней не зависят от координаты x, потому можно дополнотиельно принять, что возмущения периодичны вдоль этой оси — по сути, это близко к разложению в ряд Фурье и рассмотрению только одной компоненты:
. Такие возмущения принято называть «нормальными», хотя история этого термина довольно туманна. Подставляя указанную зависимость и записывая уравнения в проекциях на оси, получим систему для плоских возмущений. При этом, коэффициенты в ней не зависят от координаты x, потому можно дополнотиельно принять, что возмущения периодичны вдоль этой оси — по сути, это близко к разложению в ряд Фурье и рассмотрению только одной компоненты: 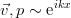 . Получается такая вот система, уже из обычных дифференциальных уравнений (штрихом обозначена производная по z):
. Получается такая вот система, уже из обычных дифференциальных уравнений (штрихом обозначена производная по z):
Опустив промежуточные преобразования, несложные, но занимающие пару страниц, укажем, что эту систему можно свести к одному уравнению для компоненты скорости w:
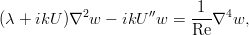
Если в нём записать комплексный инкремент и ввести фазовую скорость возмущений
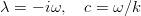
получится уравнение, известное под названием уравнения Орра-Зоммерфельда:

Вся линейная теория гидродинамической устойчивости течений базируется на этом уравнении. Правда, точных решений для него нет, независимо от вида стационарного течения и граничных условий, хотя внешне выглядит всё крайне просто и задача является замкнутой.
В решении этой задачи были разные подходы. Например, Рэлей в приближении больших чисей Рейнольдса просто пренебрёг правой частью. Конечно, это не всегда корректно, поскольку четвертые производные могут запросто компенсировать знаменатель. Правда, решить уравнение всё равно не получилось, зато получилось доказать теорему о необходимом условии устойчивости потока. Правда, для течения Пуазейля это условие не выполнено, но оно всё равно может быть неустойчивым.
Можно, в том же приближении, протянуть разложение по обратному числу Рейнольдса как малому параметру. В нулевом порядке данного разложения получится упомянутая задача Рэлея, а если пойти чуть дальше — можно поймать две кривые на плоскости параметров (k, Re), между которыми будет заключена область неустойчивости течения, в которой возмущения нарастают и приводят к разрушению стационарного профиля
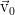 . Сперва эту проблему, для течения Пуазейля, пытался решить Гейзенберг (тот самый Вернер Гейзенберг, создатель матричной квантовой механики), но полностью довести разложение у него не получилось. В итоге, в 1944 году, за дело взялся терпеливый китаец Линь Цзя-Цзяо, протянул разложения чуть дальше и экстраполировал обе кривых, которые замкнулись в одну. Получилось у него примерно следующее (сплошная линия):
. Сперва эту проблему, для течения Пуазейля, пытался решить Гейзенберг (тот самый Вернер Гейзенберг, создатель матричной квантовой механики), но полностью довести разложение у него не получилось. В итоге, в 1944 году, за дело взялся терпеливый китаец Линь Цзя-Цзяо, протянул разложения чуть дальше и экстраполировал обе кривых, которые замкнулись в одну. Получилось у него примерно следующее (сплошная линия):
На самом деле, этот график уже немного для другой системы — вместо обычной жидкости у авторов рассматривалась суспензия некоторых волокон в канале, но смысл его тот же самый и существенных качественных отличий от теории Линя нет (иллюстрация из работы You Zhenjianga, Lin Jianzhonga, Yu Zhaoshengb. Hydrodynamic instability of fiber suspensions in channel flows. Fluid Dynamics Research, Volume 34 (4), 2004, pp. 251–271). В целом, течение Пуазейля практически для любой жидкости имеет такие свойства устойчивости, что только подчёркивает фундаментальность результатов Линя.
Примеры неустойчивостей
Ниже будут картинки, преимущественно надёрганные из «Альбома течений жидкости и газа» (М. Ван-Дайк) и просто из сети, с небольшими комментариями по конкретным постановкам задач.
Развитие неустойчивости течения Пуазейля
Этот эксперимент был проведён Рейнольдсом в 1883 г. Фотографии сделаны на той же установке, которая благополучно сохранилась, примерно сто лет спустя. Сверху вниз на фотографиях возрастает скорость течения. В поток вводится тонкая подкрашенная струйка, которая позволяет отлично визуализировать течение.
Неустойчивость жидкого столбика (задача Рэлея-Плато)
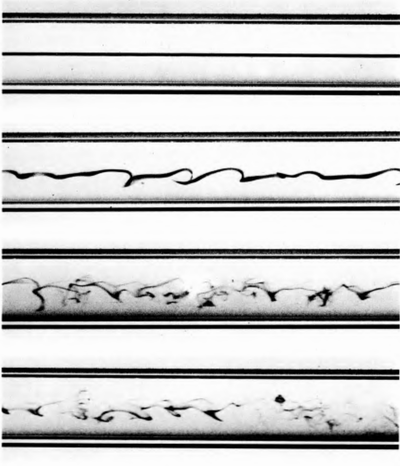
Весьма изящная неустойчивость, которую мы можем наблюдать каждый день. Достаточно открыть кран так, чтобы струйка была ровной и тонкой, но при этом достаточно длинной. За счёт взаимодействия случайных возмущений и капиллярных сил непрерывная струйка стремится разбиться на мелкие капли, т.к. это энергетически выгоднее. Здесь жидкость возмущается за счёт громкоговорителя, к которому присоединена выводящая трубка. Длина волны возмущения на нижней картинке близка к теоретическому критическому значению.
Неустойчивость Рэлея-Тейлора



Довольно незамысловатая ситуация — на поверхность лёгкой жидкости мы наливаем тяжёлую. Вполне очевидно, что тяжёлая будет стремиться «провалиться» вниз, хотя до поры до времени процессу может противостоять поверхностное натяжение. Зато когда движение начинается, происходит это очень красиво, как в лабораториях и расчётах, так и в природе (вторая картинка перевёрнута, по задумке её автора-фотохудожника).

Аналогичное явление наблюдается, если в среде существуют две области с сильно различающимися давлениями — через границу раздела между ними вещество «продавливается» и порождает аналогичные простому «проваливанию» структуры.
Вихри Тейлора


Ещё одна версия неустойчивости, чем-то по происхождению подобной рэлей-тейлоровской. Жидкость находится между двумя соосными цилиндрами и приводится в быстрое вращение. За счёт центростремительных ускорений в изначально неподвижной относительно стенок цилиндров среде формируются кольцевые ячейки с противоположными направлениями течения.
Неустойчивость Кельвина-Гельмгольца


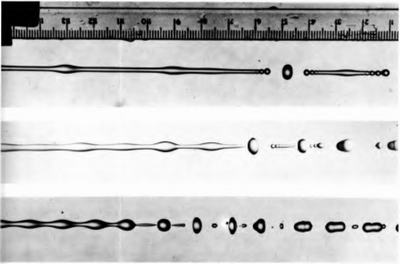
И ещё одна версия неустойчивости. Тоже, физически, весьма простая. У нас есть два потока несмешивающихся жидкостей, движущихся противоположно друг другу. Либо просто с разными скоростями — т.е. на границе раздела между ними существует скачок скорости, благодаря которому возмущения поверхности деформируются, закручиваются и порождают замысловатые вихорёчки, а потом и вовсе перемешивают жидкости. Так же интересно смотрится и в расчётах, и в экспериментальной установке, и в природе.
Здесь, конечно, показан далеко не весь спектр возможных неустойчивостей — область неисчерпаема, и содержит огромный спектр до сих пор неизученных явлений и их особенностей. Следующий пост будет о конвекции и соответствующих неустойчивостях, вызванных неоднородностью температуры в системе.








