Вместо вступления
В стандартной колоде для покера 54 карты. Без двух джокеров, которые не участвуют в игре, выходит 52 карты. Если вы хорошенько перемешаете колоду, то, возможно, создадите уникальную комбинацию из карт, которую никогда никто не создавал до вас. Потому что различных вариантов расположений 52 карт равно:
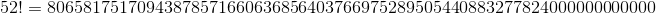

Что-то мне подсказывает, что комбинация на изображении не так уникальна.
Теперь к теме
Недавно я узнал про метод «барного развода» на игральных картах, благодаря которому «умные дяди» выигрывают приличные суммы. Суть такова:
«Разводчик» приходит в бар и некоторое время болтает с окружающими, чаще всего присоединяется к большим компаниям молодых людей. Он пытается влиться в компанию и стать «своим» среди окружающих. После того, как он заслужил некоторое доверие и к нему привыкли, разводчик выбирает самого вспыльчивого и разводит его на спор:
Я слышал, что у [блондинов/низких людей/тех, кто носит кепки/любой подходящий вариант] интуиция просто отстой! Вот спорим, что ты не сможешь угадать (в этот момент разводчик достает колоду карт) цвет каждой следующей карты? Можешь перетасовать колоду, как захочешь! За каждую угаданную карту плачу по тысяче рублей! А если не угадаешь, то ты даешь мне два рубля, потом докидываешь до четырех, до восьми рублей и дальше, ну ты понял? И чтобы было честно — остановить игру может лишь тот, кто проигрывает в общем счете, у кого выигрыш меньше. Идет?
Большинство читателей уже поняли схему и с улыбкой прикидывают сумму, которую может выиграть разводчик.
Мне стало интересно, до каких пор игрок выигрывает и как нужно действовать, чтобы увеличить шансы на выигрыш (лучший способ — отказаться от игры!). Естественно, правило про остановку игры я не учитываю, с ним выиграть невозможно.
Что к чему?
Для начала поясним ситуацию на цифрах и поймем, почему выиграть в этой игре почти невозможно. Как вы, конечно, поняли: суммы растут в разных прогрессиях. У игрока арифметическая прогрессия с шагом в тысячу (рублей). У «разводчика» же геометрическая прогрессия с знаменателем «2». Естественно, геометрическая прогрессия растет намного быстрее арифметической.
Через 10 неугаданных карт (здесь и далее неугаданная карта это неугаданный цвет карты), выигрыш разводчика будет равен 1024 рублям.
К 16 неугаданным картам, выигрыш будет равен 65536 (2^16). Это значит, что даже если игрок угадает 36 оставшиеся карты (36 000 рублей), он проиграет. Следовательно, чтобы выиграть, нужно угадать 37 карт (37 000 рублей). Тогда разводчик выиграет лишь 32 768 рублей (15 карт, 2^15) и игрок будет в плюсе. Картой меньше — и мы проиграли.
Казалось бы: угадать 37 карт на практике невозможно, так как шанс угадать 1 к 2^37

Простенький цикл на php
$cards = array(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1);
$len = count($cards);
shuffle($cards); //необязательно, но для большего соответствия
$times = 100000;
$ok = 0;
for($j = 0; $j < $times; $j++){
for($i = 0; $i < $len; $i++){
$t = mt_rand(0, 1);
if($t == $cards[$i]){
$ok += 1;
}
}
}
echo $ok / $times;
показывает, что мы и ожидаем: в среднем угадывается 26 карт (у меня при запуске вывело 25,989), а игроку нужно угадать целых 37 карт.
Но мы подбрасываем не монетку! Мы знаем, что всего в колоде 26 красных карт и 26 черных карт, следовательно, мы можем увеличить свои шансы, выбирая цвет карт, которых выпало меньше. Таким образом, если мы знаем, что в колоде осталось хотя бы на одну красную карту больше, мы выбираем красную, и наоборот.
Сделаем простенький алгоритм, который выбирает цвет карты, которых больше в колоде.
$cards = array(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1);
// 0 - красные
// 1 - черные
$len = count($cards);
shuffle($cards); //необязательно, но для большего соответствия
$times = 300000;
$ok = 0;
$red = 0; //показатель красных карт
for($j = 0; $j < $times; $j++){
for($i = 0; $i < $len; $i++){
$t = ($red > 0) ? 1 : 0; //если красных многовато, выбираем черную, иначе - красную
($cards[$i] == 0) ? $red++ : $red--; //если карта красная, то увеличиваем показатель, иначе - уменьшаем
if($t == $cards[$i]){
$ok += 1;
}
}
}
echo $ok / $times;
Если в коде есть ошибка в логике, пишите в личные сообщения, я оперативно исправлю. А также, если у вас есть алгоритм получше — пишите его в комментариях, я обязательно добавлю его.
Результат очень неоднозначен, в целом, количество угаданных карт увеличилось, у меня выводит 29-30 угаданных карт.
#coding: utf-8
@cards_booster = Array.new(52) {|idx| idx = (idx <= 25) ? 0 : 1} #создали массив колоды с мастями
10.times do
@okay_winner = 0 #обнуляем при каждом полном переборе
100000.times do #одна попытка перебрать сто тысяч раз
@cards_booster.shuffle! #каждый раз колоду тасуем
@reds = 0 #количество красных карт, допустим это единицы
@cards_booster.each do |card|
our_card = @reds > 0 ? 0 : 1 #делаем осознанный выбор карты
@okay_winner += 1 if card == our_card
@reds += (card == 1) ? 1 : -1 #красные увеличиваются если встретили красную
end
end
puts "Мы угадали масть #{@okay_winner / 100000} раз."
end
При проверке другим кодом, на Ruby вышел твердый результат: 30 (спасибо railsfun), чего тоже недостаточно для победы игрока. Что же делать в таком случае?
«Обходные» пути
Неужели нельзя выиграть у хитрого разводчика? Так как чаще всего разводчики не такие уж и умные, и дальше этой схемы они не отходят, они не знают результата при другом количестве карт. Разберем ситуации с изменением количества карт.
Естественно, игрок может высказать сомнение по поводу колоды (а вдруг там карты меняются как-нибудь?!) и предложить сыграть с новой колодой из магазина (36 карт), которую тщательно перетасуют. Разводчик, зная, что колода не суть важна, соглашается. В колоде из 36 карт же совсем другой расклад.
Чтобы разводчику выиграть, ему нужно, чтобы игрок не смог угадать 15 карт, вместо 37 из предыдущего варианта с колодой из 52 карт. Следовательно, если игрок сможет угадать 22 карты (22 000 рублей), он превысит выигрыш разводчика с его 2^14 = 16384 рублями.
Если мы запустим цикл с измененным массивом, в 36 карт, мы увидим, что среднее количество угаданных карт равно 20. Даже при изменении колоды, выиграть очень трудно, потому что игроку необходимо угадать слишком много карт. Впрочем, при единичном случае, может повезти, и игрок угадает 22+, но по статистике игрок проигрывает, в общем, всегда.
Вывод
В такой игре, выполняя все условия, выиграть в теории — маловероятно, на практике же нереально. Единственный способ — менять условия или жульничать, например, подглядеть несколько карт при тасовке.
P.S
- Шанс на выигрыш возможен лишь при отмене правила «проигрывающий останавливает игру». Тогда можно забрать выигрыш и при первом везении.
- Лучший способ не проиграть — отказаться от игры или использовать свою, меченную (крапленую) колоду (жаль не все носят крапленую колоду на этот случай)
- Предложите сыграть в такую игру друзьям. Как много из них согласятся, не заметив подвоха? Деньги у друзей можете не забирать, впрочем, по вашему желанию ;)
Спасибо vaxXxa, поменял начальные условия. Сначала разводчик получает 2 рубля, а не 1 рубль.
Спасибо lolmaus за график выигрышей, очень наглядный:
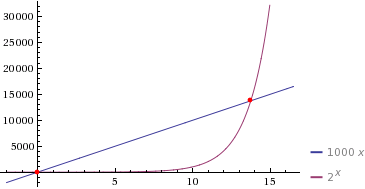
И еще у меня возник вопрос: на сколько увеличится шанс выигрыша, если во время тасовки подсмотреть одну нижнюю карту?






