В ранее опубликованном посте мы рассказывали об использовании библиотек с открытым кодом Freefem++ и NetGen в программе моделирования аэродинамических процессов. В данной статье более детально рассмотрим базовые возможности Freefem++ в качестве небольшого введения в его входной язык. Это даст начальные сведения, которые часто бывают необходимы разработчикам при выборе сторонних компонентов для включения в проектируемое приложение.
Freefem++ – это программа, предназначенная для решения математических задач на основе метода конечных элементов. Freefem++ может быть использован и в среде Windows, и в среде Linux. Официальный сайт www.freefem.org/ff++. В нашем случае использовался Freefem++ версии 3.18.-1. В комплекте архива, загружаемого с официального сайта, имеется три загрузочных модуля, назначение которых следующее:
Для выполнения FreeFem++ в фоне в составе другой программы из архива кроме загрузочного модуля требуются следующие файлы: libff.dll, libgcc_s_dw2-1.dll, libgfortran-3.dll, libgoto2.dll, libstdc++-6.dll.
При запуске загрузочного модуля Freefem++, в командной строке ему передается имя файла скрипта, написанного на специальном C-подобном языке программирования. Используя в скрипте операторы вывода или специальные функции сохранения, результаты можно записать в файл для их дальнейшего использования.
Ранее мы показали, что Freefem++ может использоваться для формирования STL описания трехмерной модели, состоящей их элементов с плоскими гранями. Для решения этой задачи надо выполнить триангуляцию граней. Рассмотрим как это делается при помощи Freefem++. Пусть требуется выполнить триангуляцию поверхности, заданной границами (см. рис. 1).

Рис. 1. Регионы поверхности
Границы областей, для которых надо выполнить триангуляцию, задаются во Freefem++ в параметрическом виде. Рассмотрим следующий код:
Во Freefem++ определены скалярные типы переменных: int, real, string, bool. Объявление переменной выполняется как в C++, при этом переменная может быть инициализирована, как это сделано для переменной n.
Границы задаются фрагментами при помощи параметризованных линий. Для этого предназначен тип border. Фрагменты границ могут пересекаться только на концах. Объявление фрагмента границы включает в себя идентификатор границы, границы изменения параметра (в данном случае это параметр t) и выражения для изменения координат x и y в зависимости от параметра. В примере все фрагменты – отрезки.
Последний оператор в рассмотренном коде – plot, он предназначен для графического отображения данных определенных типов. В данном случае он отображает границу, состоящую из фрагментов границ. Фрагменты границы объединяются в общую границу с помощью оператора +. Для каждого фрагмента указывается параметр, задающий количество частей, на которые фрагмент должен быть разделен. Этот параметр будет еще раз рассмотрен ниже в другом контексте. Результат выполнения указанного оператора plot показан на рис. 2.
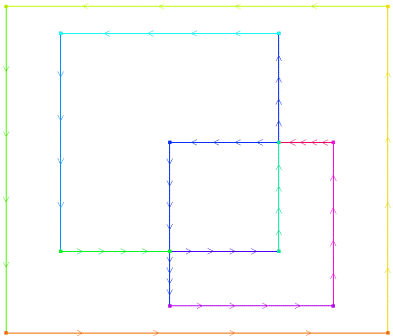
Рис. 2. Границы регионов поверхности, отображаемые оператором plot
Теперь добавим код, выполняющий триангуляцию. На рис. 3 показан результат его выполнения.
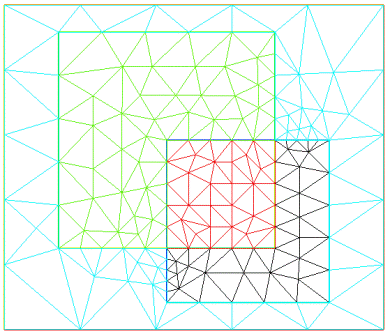
Рис. 3. Результат триангуляции
В этом коде вводится переменная Th типа mesh. Тип mesh является программной моделью триангуляционной сетки. Для получения объекта этого типа в данном случае используется функция buildmesh, которой на вход передается граница разбиваемых областей. Функции buildmesh можно передать необязательный параметр fixeborder, использование которого гарантирует, что точки на линии не будут изменены в процессе триангуляции. Второй оператор – plot — в данном случае принимает на входе объект типа mesh и показывает сетку элементов в графическом окне (рис. 3).
Как уже было показано, граница представляется как сумма фрагментов границ, имеющих тип border. Параметр, указанный для каждого фрагмента, здесь имеет двойное назначение. Во-первых, он указывает, на сколько частей разбивается фрагмент границы для построения сетки. Каждая часть фрагмента границы станет стороной треугольника формируемой сетки. Во-вторых, знак параметра указывает ту область, которая должна подвергнуться триангуляции. Если параметр положительный, то триангуляция выполняется слева от фрагмента границы. Если же он отрицательный, то триангуляция выполняется справа от границы. Поясним это на примере. Если бы в приведенном коде граница была задана так: b0(n) + b1(n) + b2(n) + b3(n) + b4(n) + b5(-2) + b6(n) + b7(n) + b8(n) + b9(-2) + b10(n) + b11(n) + b12(n) + b13(-2) + b14(-2) + b15(n), где для b5, b9, b13 и b14 задано разбиение на два отрезка с отрицательным значением, то триангуляция была бы выполнена так, как показано на рис. 4.
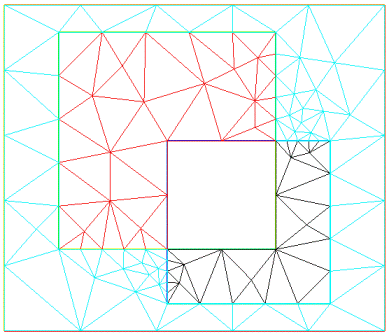
Рис. 4. Триангуляция с пустой подобластью
Добавим код, демонстрирующий операции с переменной типа mesh, оператор цикла и вывод в файл.
Для вывода данных в файл предусмотрен тип ofstream, аналог файлового выходного потока из библиотеки fstream для C++. При инициализации файловой переменной надо указать имя файла. Если требуется только добавлять данные в файл, то нужно указать второй параметр инициализации append. С файловой переменной можно выполнить ряд операций. В примере с помощью функции precision устанавливается количество выводимых цифр после десятичного разделятеля. Имеется еще несколько функций, управляющих форматом вывода, аналогичных манипуляторам из библиотеки iostream. Оператор << позволяет выводить в файл значения переменных скалярных типов. В символьной строке можно использовать символ конца строки '\n', либо с этой целью выводить глобальную переменную endl.
В приведенном коде имеется оператор цикла for, который полностью повторяет логику оператора for в C++. Операторы инкремента и декремента также повторяют аналогичные операторы C++.
Freefem++ предоставляет доступ к различным свойствам сетки элементов, представляемым типом mesh. Здесь же заметим, что Freefem++ предоставляет одинаковые интерфейсы для работы и с двумерной сеткой типа mesh, и с трехмерной сеткой типа mesh3. Поэтому здесь рассмотрим этот интерфейс для двух указанных типов, чтобы позже не повторять его описания для mesh3. Как видно из примера, свойство nt возвращает количество элементов сетки (треугольников для mesh или тетраэдров для mesh3). Также можно получить количество точек сетки — свойство nv, количество граничных элементов — nbe.
К объекту типа mesh или mesh3 могут применяться два вида индексирования: индексирование с квадратными скобками "[]" и индексирование с круглыми скобками "()". Первое из них дает элемент сетки (треугольник для mesh или тетраэдр для mesh3) с заданным индексом. Таким образом, Th[i] — элемент сетки (треугольник в данном примере), к которому, в свою очередь, применены определенные функции, предусмотренные для элемента. "()"-индексирование предоставляет вершину с заданным индексом. К вершине могут быть применены операции получения ее координат. К элементу сетки применяются следующие функции: индексирование для получения вершин элемента, получение метки.
Freefem++ определяет тип mesh3 для 3D-сетки. Такую сетку можно получить с помощью функций генерации. Например, функция buildlayers() позволяет сформировать 3D-сетку путем вытягивания 2D-триангуляции по оси Z. Однако во Freefem++ нет собственного генератора. Для этих целей используется сторонний генератор TetGen (официальный сайт wias-berlin.de/software/tetgen ), а соответствующие функции Freefem++ — программный интерфейс к этому генератору. TetGen не может использоваться в коммерческих проектах без разрешения автора. Но если такая лицензия создает проблему, то можно воспользоваться другим генератором сетки. Freefem++ имеет возможность импорта 3D-сетки из файла, соответствующего формату mesh. mesh-файл имеет следующий формат:
mesh-файл импортируется при помощи функции readmesh3, которой указывается имя файла:
Для импорта сетки из mesh-файла оказывается критичным порядок следования номеров вершин тетраэдров. В исходном коде Freefem++ в файле Mesh3dn.hpp можно найти структуру DataTet, в которой имеется метод вычисления объема тетраэдра mesure(). Если вершины тетраэдра в mesh-файле следуют в таком порядке, что вычисленный объем оказывается отрицательным, то Freefem++ завершается с ошибкой. Поэтому вершины в mesh-файле должны быть перечислены так, чтобы данная ситуация не возникала.
При необходимости, сетка может быть отображена в графическом окне функцией plot (см. рис. 5).
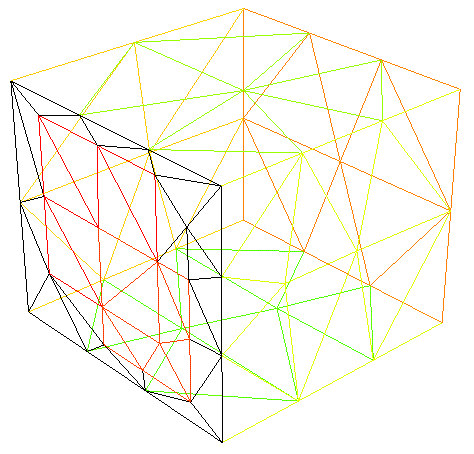
Рис. 5. Отображение 3D-сетки функцией plot
Основное назначение Freefem++ – решение систем дифференциальных уравнений в частных производных методом конечных элементов. Для этого функции, участвующие в системе уравнений, определяются на сетке конечных элементов. Freefem++ позволяет определить тип FE-пространства (конечно-элементное пространство). В соответствии с типом пространства вводятся объекты функций определенного пространства. Например,
где Vh — тип пространства на сетке Th, f — функция на этом пространстве.
При объявлении типа кончено-элементного пространства указывается базис для элементов. Он может принимать значения P03d — кусочно-постоянный, P13d — кусочно-линейный, P23d — кусочно квадратичный и т.п. На рис. 6 показана функция из примера с квадратичным базисом, а на рис. 7 — та же функция с линейным базисом и с заметными искажениями.
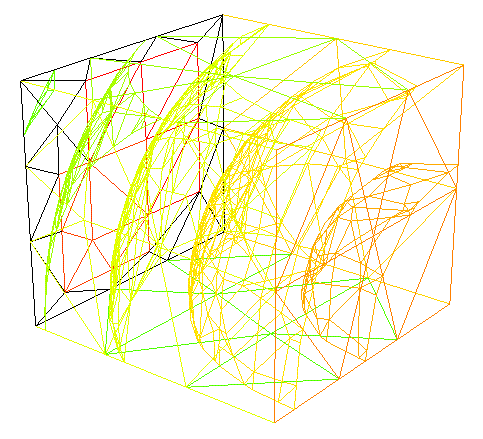
Рис. 6. Конечно-элементная функция с квадратичным базисом
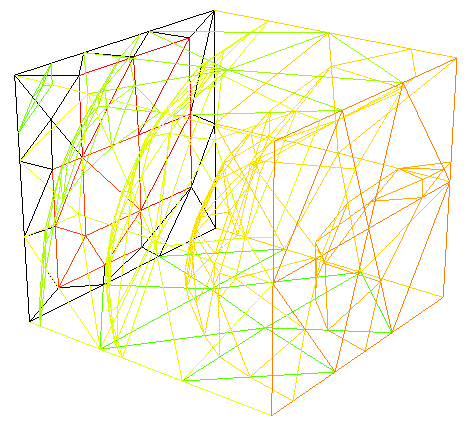
Рис. 7. Конечно-элементная функция с линейным базисом
Для решения системы уравнений в частных производных во Freefem++ задается вариационная постановка задачи, при решении задачи формируются искомые функции. На основе нижеследующего скрипта рассмотрим как записывается вариационная формулировка и другие элементы программирования.
В этом примере представлены следующие конструкции. Конечно-элементное пространство может быть задано для векторного поля. В примере пространство VVh задается для векторного поля с четырьмя компонентами, а Vh для скалярного поля.
Freefem++ предоставляет возможность объявления макросов, которые начинаются с ключевого слова macro. При макроподстановке имя макроса будет заменено на тело макроса с заменой формальных параметров на фактические. В примере имеется два макроса: Grad(u) и div(u1, u2, u3). В этих макросах используются специальные обозначения dx, du, dz, которые обозначают дифференциалы по соответствующим координатам.
Функция объявляется при помощи ключевого слова func. Причем, если аргументы функции обозначаются через x, y, z, которые являются зарезервированными словами, то указывать формальные параметры не нужно.
Конструкция solve служит для записи вариационной формулировки и решения задачи. После имени задачи перечисляются неизвестные и тестовые функции. В данном случае в задаче Prob имеется две векторные функции, определяемые на пространстве VVh: [u1, u2, u3, p] — искомая и [v1, v2, v3, q] — пробная. После знака равенства записывается выражение для вариационной формулировки. В примере в этом месте имеется две специфические конструкции Freefem++. Для записи трехмерного интеграла используется специальная конструкция int3d, в которой задается пространство интегрирования, в данном случае это сетка Th. Кроме этого, здесь используется оператор транспонирования матрицы, обозначаемый апострофом. В конце вариационной формулировки в конструкции solve записываются граничные условия. Граничное условие обозначается специальным словом on, после которого в скобках указывается метка соответствующий области из объекта класса mesh3. Запись этих меток в mesh-файл была рассмотрена выше. Для области перечисляются компоненты искомого поля и для каждого из них записывается ограничение. Ограничение может быть произвольным выражением. В примере в качестве ограничения задаются числа и функция fup.
При выводе компонента поля при помощи функции plot, в графическом окне показывается кончено-элементное пространство с изоповерхностями, как показано на рис. 8. Количество изоповерхностей можно задавать параметром nbiso в скрипте, а потом изменять вручную в графическом окне.

Рис. 8. Результат решения
Freefem++ является мощным средством решения математических задач, которое можно использовать при разработке приложений, в том числе и коммерческих. В последнем случае полезным свойством Freefem++ является возможность импорта 3D-сетки конечных элементов, что позволяет использовать сторонние генераторы сеток.
Получение и выполнение Freefem++
Freefem++ – это программа, предназначенная для решения математических задач на основе метода конечных элементов. Freefem++ может быть использован и в среде Windows, и в среде Linux. Официальный сайт www.freefem.org/ff++. В нашем случае использовался Freefem++ версии 3.18.-1. В комплекте архива, загружаемого с официального сайта, имеется три загрузочных модуля, назначение которых следующее:
- FreeFem++.exe – полноценный вариант программы, который при необходимости отображает графическое окно с результатами решения. При необходимости при вызове можно указать два ключа: -nowait для того, чтобы Freefem++ завершился без подтверждения завершения пользователем, и -nw — для отказа от отображения графического окна с результатами решения.
- FreeFem++-mpi.exe – для распараллеливания вычислений на базе MPI.
- FreeFem++-nw.exe – для вызова из приложений, игнорирует графический вывод результатов. Для того, чтобы он еще и не ожидал подтверждения завершения работы с программой, нужно указать в командной строке ключ -nowait.
Для выполнения FreeFem++ в фоне в составе другой программы из архива кроме загрузочного модуля требуются следующие файлы: libff.dll, libgcc_s_dw2-1.dll, libgfortran-3.dll, libgoto2.dll, libstdc++-6.dll.
При запуске загрузочного модуля Freefem++, в командной строке ему передается имя файла скрипта, написанного на специальном C-подобном языке программирования. Используя в скрипте операторы вывода или специальные функции сохранения, результаты можно записать в файл для их дальнейшего использования.
2D-триангуляция
Ранее мы показали, что Freefem++ может использоваться для формирования STL описания трехмерной модели, состоящей их элементов с плоскими гранями. Для решения этой задачи надо выполнить триангуляцию граней. Рассмотрим как это делается при помощи Freefem++. Пусть требуется выполнить триангуляцию поверхности, заданной границами (см. рис. 1).

Рис. 1. Регионы поверхности
Границы областей, для которых надо выполнить триангуляцию, задаются во Freefem++ в параметрическом виде. Рассмотрим следующий код:
int n = 5;
border b0(t=0,1){x = 7 * t; y = 0; }
border b1(t=0,1){x = 7; y = 0 + 6 * t; }
border b2(t=0,1){x = 7 - 7 * t; y = 6; }
border b3(t=0,1){x = 0; y = 6 - 6 * t; }
border b4(t=0,1){x = 1 + 2 * t; y = 1.5; }
border b5(t=0,1){x = 5; y = 1.5 + 2 * t; }
border b6(t=0,1){x = 5 - 4 * t; y = 5.5; }
border b7(t=0,1){x = 1; y = 5.5 - 4 * t; }
border b8(t=0,1){x = 5; y = 3.5 + 2 * t; }
border b9(t=0,1){x = 3 + 2 * t; y = 1.5; }
border b10(t=0,1){x = 3 + 3 * t; y = 0.5; }
border b11(t=0,1){x = 6; y = 0.5 + 3 * t; }
border b12(t=0,1){x = 6 - 1 * t; y = 3.5; }
border b13(t=0,1){x = 3; y = 3.5 - 2 * t; }
border b14(t=0,1){x = 5 - 2 * t; y = 3.5; }
border b15(t=0,1){x = 3; y = 1.5 - 1 * t; }
plot(b0(n) + b1(n) + b2(n) + b3(n) + b4(n) + b5(n) + b6(n) + b7(n) + b8(n) + b9(n) + b10(n)
+ b11(n) + b12(n) + b13(n) + b14(n) + b15(n));Во Freefem++ определены скалярные типы переменных: int, real, string, bool. Объявление переменной выполняется как в C++, при этом переменная может быть инициализирована, как это сделано для переменной n.
Границы задаются фрагментами при помощи параметризованных линий. Для этого предназначен тип border. Фрагменты границ могут пересекаться только на концах. Объявление фрагмента границы включает в себя идентификатор границы, границы изменения параметра (в данном случае это параметр t) и выражения для изменения координат x и y в зависимости от параметра. В примере все фрагменты – отрезки.
Последний оператор в рассмотренном коде – plot, он предназначен для графического отображения данных определенных типов. В данном случае он отображает границу, состоящую из фрагментов границ. Фрагменты границы объединяются в общую границу с помощью оператора +. Для каждого фрагмента указывается параметр, задающий количество частей, на которые фрагмент должен быть разделен. Этот параметр будет еще раз рассмотрен ниже в другом контексте. Результат выполнения указанного оператора plot показан на рис. 2.

Рис. 2. Границы регионов поверхности, отображаемые оператором plot
Теперь добавим код, выполняющий триангуляцию. На рис. 3 показан результат его выполнения.
mesh Th = buildmesh(b0(n) + b1(n) + b2(n) + b3(n) + b4(n) + b5(n) + b6(n) + b7(n) + b8(n) + b9(n) + b10(n) + b11(n) + b12(n) + b13(n) + b14(n) + b15(n), fixeborder=1); plot(Th);

Рис. 3. Результат триангуляции
В этом коде вводится переменная Th типа mesh. Тип mesh является программной моделью триангуляционной сетки. Для получения объекта этого типа в данном случае используется функция buildmesh, которой на вход передается граница разбиваемых областей. Функции buildmesh можно передать необязательный параметр fixeborder, использование которого гарантирует, что точки на линии не будут изменены в процессе триангуляции. Второй оператор – plot — в данном случае принимает на входе объект типа mesh и показывает сетку элементов в графическом окне (рис. 3).
Как уже было показано, граница представляется как сумма фрагментов границ, имеющих тип border. Параметр, указанный для каждого фрагмента, здесь имеет двойное назначение. Во-первых, он указывает, на сколько частей разбивается фрагмент границы для построения сетки. Каждая часть фрагмента границы станет стороной треугольника формируемой сетки. Во-вторых, знак параметра указывает ту область, которая должна подвергнуться триангуляции. Если параметр положительный, то триангуляция выполняется слева от фрагмента границы. Если же он отрицательный, то триангуляция выполняется справа от границы. Поясним это на примере. Если бы в приведенном коде граница была задана так: b0(n) + b1(n) + b2(n) + b3(n) + b4(n) + b5(-2) + b6(n) + b7(n) + b8(n) + b9(-2) + b10(n) + b11(n) + b12(n) + b13(-2) + b14(-2) + b15(n), где для b5, b9, b13 и b14 задано разбиение на два отрезка с отрицательным значением, то триангуляция была бы выполнена так, как показано на рис. 4.

Рис. 4. Триангуляция с пустой подобластью
Добавим код, демонстрирующий операции с переменной типа mesh, оператор цикла и вывод в файл.
ofstream fout("triangulation.out");
fout.precision(14);
fout << Th.nt << endl;
for(int i = 0; i < Th.nt; i++ )
{
fout
<< Th[i][0].x << " "
<< Th[i][0].y << " "
<< Th[i][1].x << " "
<< Th[i][1].y << " "
<< Th[i][2].x << " "
<< Th[i][2].y << " "
<< endl;
}
Для вывода данных в файл предусмотрен тип ofstream, аналог файлового выходного потока из библиотеки fstream для C++. При инициализации файловой переменной надо указать имя файла. Если требуется только добавлять данные в файл, то нужно указать второй параметр инициализации append. С файловой переменной можно выполнить ряд операций. В примере с помощью функции precision устанавливается количество выводимых цифр после десятичного разделятеля. Имеется еще несколько функций, управляющих форматом вывода, аналогичных манипуляторам из библиотеки iostream. Оператор << позволяет выводить в файл значения переменных скалярных типов. В символьной строке можно использовать символ конца строки '\n', либо с этой целью выводить глобальную переменную endl.
В приведенном коде имеется оператор цикла for, который полностью повторяет логику оператора for в C++. Операторы инкремента и декремента также повторяют аналогичные операторы C++.
Freefem++ предоставляет доступ к различным свойствам сетки элементов, представляемым типом mesh. Здесь же заметим, что Freefem++ предоставляет одинаковые интерфейсы для работы и с двумерной сеткой типа mesh, и с трехмерной сеткой типа mesh3. Поэтому здесь рассмотрим этот интерфейс для двух указанных типов, чтобы позже не повторять его описания для mesh3. Как видно из примера, свойство nt возвращает количество элементов сетки (треугольников для mesh или тетраэдров для mesh3). Также можно получить количество точек сетки — свойство nv, количество граничных элементов — nbe.
К объекту типа mesh или mesh3 могут применяться два вида индексирования: индексирование с квадратными скобками "[]" и индексирование с круглыми скобками "()". Первое из них дает элемент сетки (треугольник для mesh или тетраэдр для mesh3) с заданным индексом. Таким образом, Th[i] — элемент сетки (треугольник в данном примере), к которому, в свою очередь, применены определенные функции, предусмотренные для элемента. "()"-индексирование предоставляет вершину с заданным индексом. К вершине могут быть применены операции получения ее координат. К элементу сетки применяются следующие функции: индексирование для получения вершин элемента, получение метки.
3D-сетка
Freefem++ определяет тип mesh3 для 3D-сетки. Такую сетку можно получить с помощью функций генерации. Например, функция buildlayers() позволяет сформировать 3D-сетку путем вытягивания 2D-триангуляции по оси Z. Однако во Freefem++ нет собственного генератора. Для этих целей используется сторонний генератор TetGen (официальный сайт wias-berlin.de/software/tetgen ), а соответствующие функции Freefem++ — программный интерфейс к этому генератору. TetGen не может использоваться в коммерческих проектах без разрешения автора. Но если такая лицензия создает проблему, то можно воспользоваться другим генератором сетки. Freefem++ имеет возможность импорта 3D-сетки из файла, соответствующего формату mesh. mesh-файл имеет следующий формат:
- В начале файла записывается информация о версии формата (MeshVersionFormatted 1), размерность пространства (Dimension 3).
MeshVersionFormatted 1 Dimension 3
- После ключевого слова Vertices указывается количество вершин сетки и перечисляются вершины, для которых указываются координаты по X, Y, Z и метка вершины.
Vertices 65 7 5 1.5 0 7 3 1.5 0 7 3 0.5 0 7 5 3.5 0 ...
- После ключевого слова Tetrahedra указывается количество элементов сетки и перечисляются элементы, для которых записываются четыре номера вершин и метка.
Tetrahedra 185 52 56 49 50 0 3 18 14 61 0 47 64 57 54 0 ...
- После ключевого слова Triangles записывается количество граничных треугольников. Для каждого треугольника перечисляются номера вершин узлов сетки, являющихся вершинами этих треугольников, и указывается метка границы.
Triangles 96 2 3 8 2 2 8 1 2 4 1 7 2 ...
- Файл завершается ключевым словом End
mesh-файл импортируется при помощи функции readmesh3, которой указывается имя файла:
mesh3 Th;
Th = readmesh3("example3d.mesh");
plot(Th);
Для импорта сетки из mesh-файла оказывается критичным порядок следования номеров вершин тетраэдров. В исходном коде Freefem++ в файле Mesh3dn.hpp можно найти структуру DataTet, в которой имеется метод вычисления объема тетраэдра mesure(). Если вершины тетраэдра в mesh-файле следуют в таком порядке, что вычисленный объем оказывается отрицательным, то Freefem++ завершается с ошибкой. Поэтому вершины в mesh-файле должны быть перечислены так, чтобы данная ситуация не возникала.
При необходимости, сетка может быть отображена в графическом окне функцией plot (см. рис. 5).

Рис. 5. Отображение 3D-сетки функцией plot
Решение систем дифференциальных уравнений
Основное назначение Freefem++ – решение систем дифференциальных уравнений в частных производных методом конечных элементов. Для этого функции, участвующие в системе уравнений, определяются на сетке конечных элементов. Freefem++ позволяет определить тип FE-пространства (конечно-элементное пространство). В соответствии с типом пространства вводятся объекты функций определенного пространства. Например,
fespace Vh(Th, P23d);
Vh f = x^2 + y^2 + z^2; где Vh — тип пространства на сетке Th, f — функция на этом пространстве.
При объявлении типа кончено-элементного пространства указывается базис для элементов. Он может принимать значения P03d — кусочно-постоянный, P13d — кусочно-линейный, P23d — кусочно квадратичный и т.п. На рис. 6 показана функция из примера с квадратичным базисом, а на рис. 7 — та же функция с линейным базисом и с заметными искажениями.

Рис. 6. Конечно-элементная функция с квадратичным базисом

Рис. 7. Конечно-элементная функция с линейным базисом
Для решения системы уравнений в частных производных во Freefem++ задается вариационная постановка задачи, при решении задачи формируются искомые функции. На основе нижеследующего скрипта рассмотрим как записывается вариационная формулировка и другие элементы программирования.
mesh3 Th = readmesh3("example3d.mesh");
fespace VVh(Th, [P2,P2,P2,P1]);
fespace Vh(Th, P23d);
macro Grad(u) [dx(u),dy(u),dz(u)] //
macro div(u1,u2,u3) (dx(u1)+dy(u2)+dz(u3)) //
VVh [u1,u2,u3,p];
VVh [v1,v2,v3,q];
func fup = (1-x)*(x)*y*(1-y)*16;
solve Prob([u1,u2,u3,p],[v1,v2,v3,q]) =
int3d(Th,qforder=3)( Grad(u1)'*Grad(v1) + Grad(u2)'*Grad(v2) + Grad(u3)'*Grad(v3)
- div(u1,u2,u3)*q - div(v1,v2,v3)*p + 1e-10*q*p )
+ on(5,u1=0, u2=0, u3=0)
+ on(1,u1=fup, u2=0, u3=0) ;
plot(p, nbiso=10);
В этом примере представлены следующие конструкции. Конечно-элементное пространство может быть задано для векторного поля. В примере пространство VVh задается для векторного поля с четырьмя компонентами, а Vh для скалярного поля.
Freefem++ предоставляет возможность объявления макросов, которые начинаются с ключевого слова macro. При макроподстановке имя макроса будет заменено на тело макроса с заменой формальных параметров на фактические. В примере имеется два макроса: Grad(u) и div(u1, u2, u3). В этих макросах используются специальные обозначения dx, du, dz, которые обозначают дифференциалы по соответствующим координатам.
Функция объявляется при помощи ключевого слова func. Причем, если аргументы функции обозначаются через x, y, z, которые являются зарезервированными словами, то указывать формальные параметры не нужно.
Конструкция solve служит для записи вариационной формулировки и решения задачи. После имени задачи перечисляются неизвестные и тестовые функции. В данном случае в задаче Prob имеется две векторные функции, определяемые на пространстве VVh: [u1, u2, u3, p] — искомая и [v1, v2, v3, q] — пробная. После знака равенства записывается выражение для вариационной формулировки. В примере в этом месте имеется две специфические конструкции Freefem++. Для записи трехмерного интеграла используется специальная конструкция int3d, в которой задается пространство интегрирования, в данном случае это сетка Th. Кроме этого, здесь используется оператор транспонирования матрицы, обозначаемый апострофом. В конце вариационной формулировки в конструкции solve записываются граничные условия. Граничное условие обозначается специальным словом on, после которого в скобках указывается метка соответствующий области из объекта класса mesh3. Запись этих меток в mesh-файл была рассмотрена выше. Для области перечисляются компоненты искомого поля и для каждого из них записывается ограничение. Ограничение может быть произвольным выражением. В примере в качестве ограничения задаются числа и функция fup.
При выводе компонента поля при помощи функции plot, в графическом окне показывается кончено-элементное пространство с изоповерхностями, как показано на рис. 8. Количество изоповерхностей можно задавать параметром nbiso в скрипте, а потом изменять вручную в графическом окне.

Рис. 8. Результат решения
Выводы
Freefem++ является мощным средством решения математических задач, которое можно использовать при разработке приложений, в том числе и коммерческих. В последнем случае полезным свойством Freefem++ является возможность импорта 3D-сетки конечных элементов, что позволяет использовать сторонние генераторы сеток.






