Комментарии 8
Спасибо. Довольно содержательная статья на эту избитую тему.
Вы не могли бы выложить итоговый код с оптимизациями поиска максимального пути без самопересечений?
Вы не могли бы выложить итоговый код с оптимизациями поиска максимального пути без самопересечений?
+1
Заранее извиняюсь за стиль.
Код dfs'а на Delphi
function g(v: integer): integer;
var
i: integer;
begin
result := 1;
if (vis2 and (1 shl (v - 1)) = 0) then
vis2 := vis2 + (1 shl (v - 1));
for i := 1 to n do
if (vis2 and (1 shl (i - 1)) = 0) and (matrix[v][i] = 1) then
result := result + g(i);
end;
function dfs(v, deep: integer): integer;
var
i, cnt, top: integer;
begin
vis := vis + (1 shl (v - 1));
result := get_ans_by_key(vis, v);
if result <> -1 then
exit;
result := deep;
global_ans := max(global_ans, result);
for i := 1 to n do
vis2[i] := vis[i];
cnt := g(v);
if deep + cnt - 1 > global_ans then begin
top := 0;
for i := 1 to n do
if (matrix[v][i] = 1) and (vis and (1 shl (i - 1)) = 0) then begin
inc(top);
res[top] := dfs2(i);
id[top] := i;
end;
if top <> 0 then begin
qsort(1, top);
for i := 1 to min(k, top) do
if (matrix[v][id[i]] = 1) and (vis and (1 shl (id[i] - 1)) = 0) then
result := max(result, dfs(id[i], deep + 1));
end;
end;
put_key(vis, v, result);
vis := vis - (1 shl (v - 1));
end;
0
Для себя какое-то время назад открыл замечательную книгу — Skiena. The Algorithm Design Manual. Вот в ней об алгоритмах, в частности о графах и эвристиках оптимизации NP задач много, интересно и понятно. Рекомендую.
+2
Прикольно. Правда, не понятно, в какой момент пора искать в ширину для конкретной задачи? Или как понять, что алгоритм «не очень» подходит?
Есть еще прикольные эвристики, типа муравьиного алгоритма.
Есть еще прикольные эвристики, типа муравьиного алгоритма.
0
Начнём с того, что всё что написано в статье — эвристики. Это значит, что точного доказательства, а значит и отношения оптимального времени работы dfs'а и bfs'а вам вряд ли кто-то скажет. Тем более, оно точно варьируется от задачи к задачи и от качества функции g(s).
На практике нужно экспериментировать с разными константами. Возможно есть какой-то научный подход, но я его не знаю.
На практике нужно экспериментировать с разными константами. Возможно есть какой-то научный подход, но я его не знаю.
0
Когда-то в университете я писал программу сравнения разных методов поиска кратчайшего пути в графе.
Интерфейс, правда, на литовском языке, но, думаю, это не принципиально.
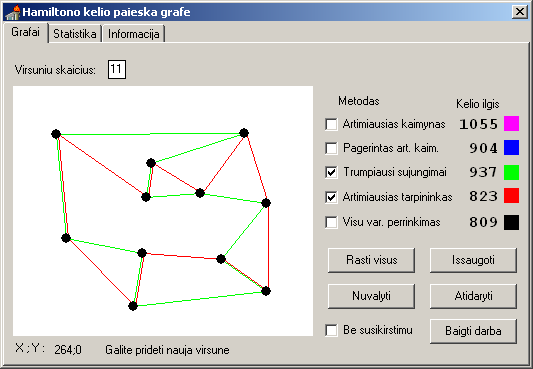
Переведу методы поиска:
1. Алгоритм ближайшего соседа.
2. Улучшенный алг. ближайшего соседа
3. Алгоритм ближайших соседей
4. Алгоритм ближайшего посредника
5. Перебор всех вариантов.
Галочка — улучшить поиск (искать без пересечений)
Программой просто и удобно пользоваться. Можно скачать и попробовать. Третья программа в списке.
Интерфейс, правда, на литовском языке, но, думаю, это не принципиально.

Переведу методы поиска:
1. Алгоритм ближайшего соседа.
2. Улучшенный алг. ближайшего соседа
3. Алгоритм ближайших соседей
4. Алгоритм ближайшего посредника
5. Перебор всех вариантов.
Галочка — улучшить поиск (искать без пересечений)
Программой просто и удобно пользоваться. Можно скачать и попробовать. Третья программа в списке.
0
Судя по названию файла «delphi_hamilton.exe» и по скриншоту это всё-таки не «сравнение разных методов поиска кратчайшего пути в графе», а сравнение разных эвристических методов поиска гамильтонового цикла, видимо кратчайшего, да ещё и, кажется, в полном графе. Из вашего описания это не вполне ясно. Хотя да, задача звучит занимательно.
+1
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Оптимизация перебора