Open FOAM
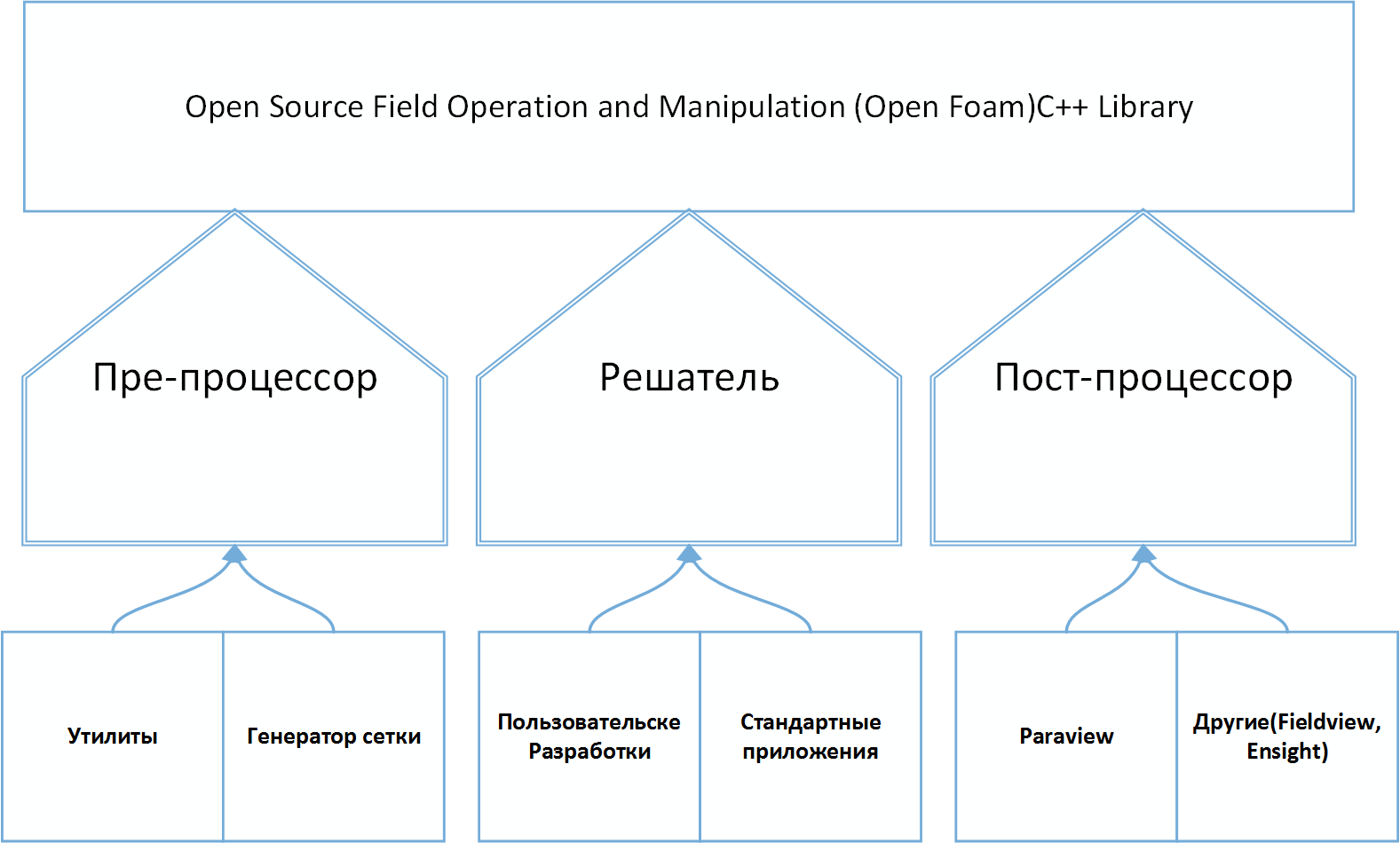
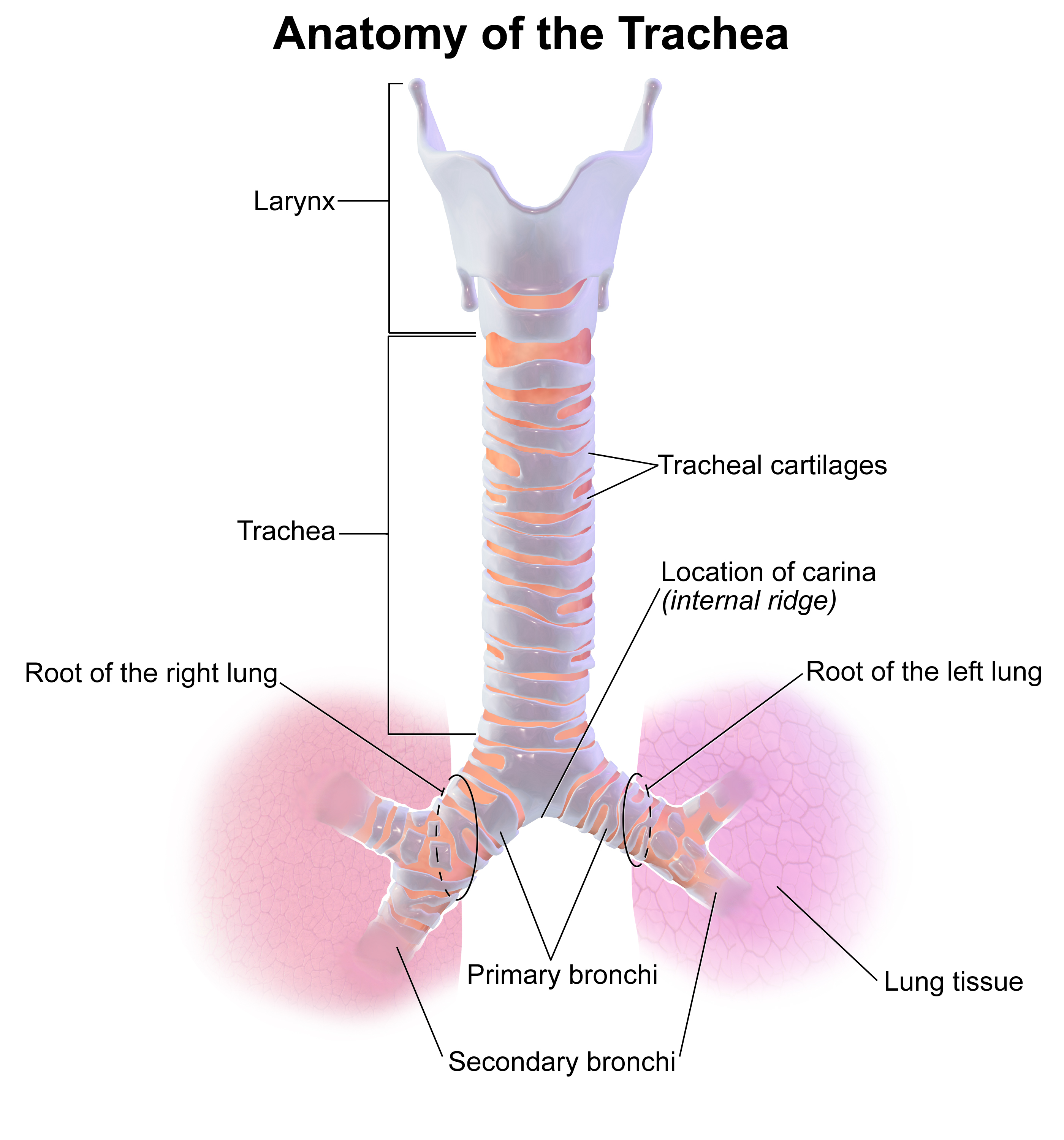
OpenFOAM — свободно распространяемый инструментарий вычислительной гидродинамики для операций с полями (скалярными, векторными и тензорными). На сегодня является одним из «законченных» и известных приложений, предназначенных для FVM-вычислений.В частности пакет позволяет решать задачи гидродинамики ньютоновских и неньютоновских вязких жидкостей как в несжимаемом, так и сжимаемом приближении с учётом конвективного теплообмена и действием сил гравитации. Для моделирования турбулентных течений возможно использование RANS-моделей, LES- и DNS-методов. Возможно решение дозвуковых, околозвуковых и сверхзвуковых задач.
В основе пакета лежит набор библиотек, предоставляющих инструменты для решения систем дифференциальных уравнений в частных производных как в пространстве, так и во времени. Рабочим языком кода является ООП C++. В терминах данного языка большинство математических дифференциальных и тензорных операторов в программном коде (до трансляции в исполняемый файл) уравнений может быть представлено в удобочитаемой форме, а метод дискретизации и решения для каждого оператора может быть выбран уже пользователем в процессе расчёта. Таким образом, в коде полностью инкапсулируются и разделяются понятия расчетной сетки (метод дискретизации), дискретизации основных уравнений и методов решения алгебраических уравнений.
Задача
Решим задачу обтекании бесконечного квадратного цилиндра.Жидкость несжимаемая и вязкая.
Для подобных задач множество экспериментальных данных. Поэтому в конце мы сможем сравнить результаты численного моделирования.
Где U=(u,v)-безразмерная скорость,p -безразмерное давление, Re — число Рейнольдса.
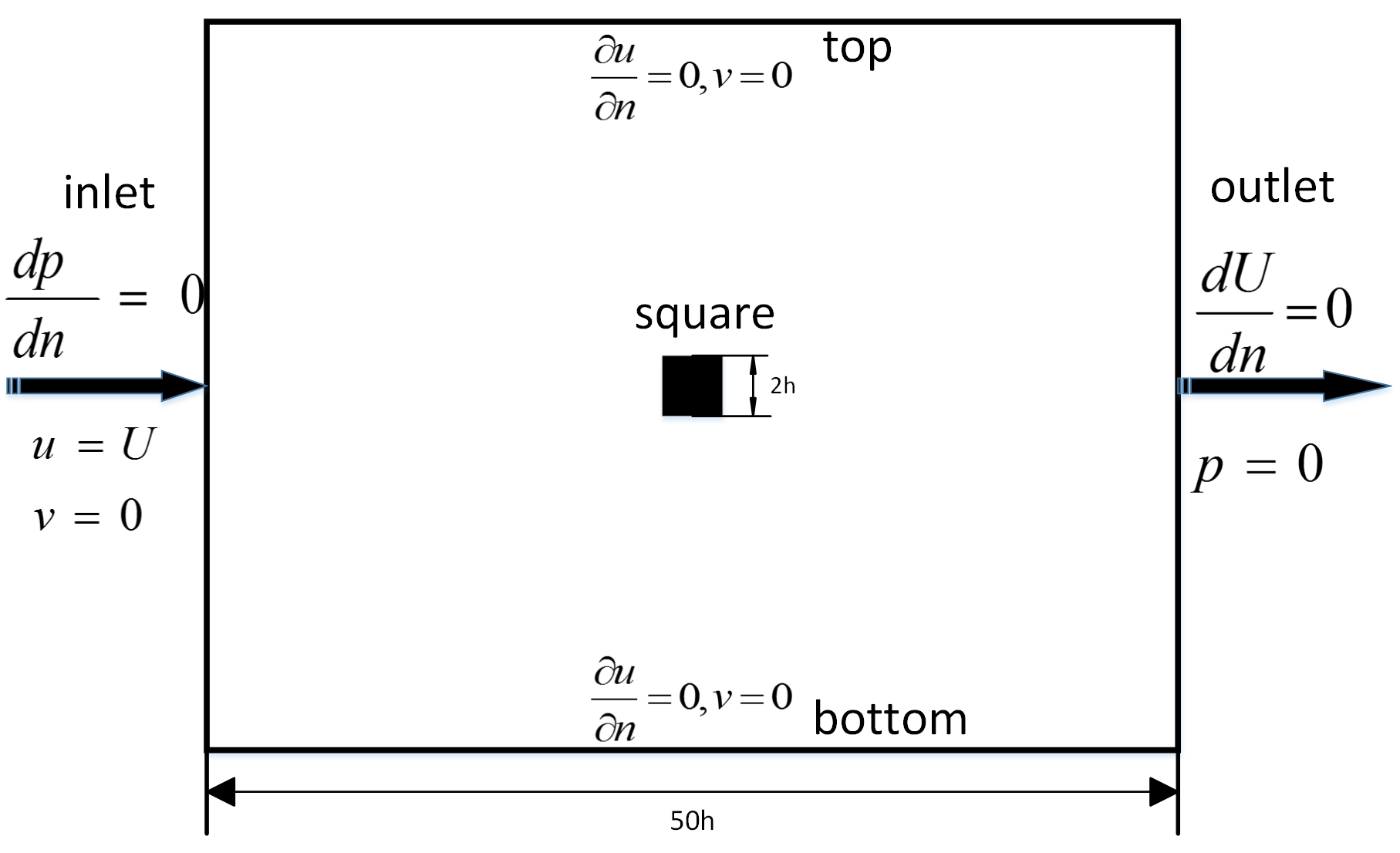
Для дискретизации расчетной области используются блочные сетки. Построение производиться средствами утилиты blockmesh, пакета OpenFOAM. Область разбивается на непересекающиеся ячейки, имеющие кубическую форму. Для учета двухмерности на передней «front» и на задней границе области «back», параллельных плоскости течения, используются специальные граничные условия.
| Граница | Переменная | Тип граничных условий |
| «Front», «back» | U, p | empty |
| «Inlet», «outlet» | U | FixedValue |
| «Inlet», «outlet» | p | FixedValue |
| «Bottom», «top» | U | ZeroGradient |
| «Bottom», «top» | p | ZeroGradient |
| «Square» | U | ZeroGradient |
| «Square» | p | FixedValue |
Схема разбиения
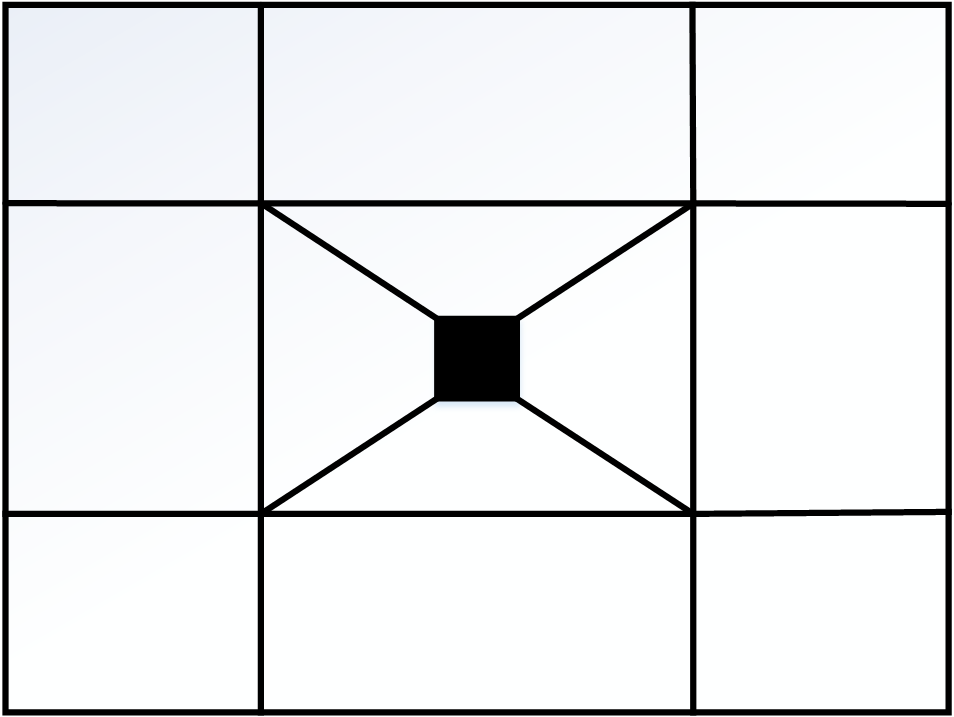
Бесконечная область заменяется ограниченной областью, которая представляет собой прямоугольный параллелепипед, в центре которой помещен квадратный цилиндр. Выбор трехмерной области решения проводиться в соответствии с особенностью программного обеспечения. В OpenFOAM не предусмотрено решение 2D задач.
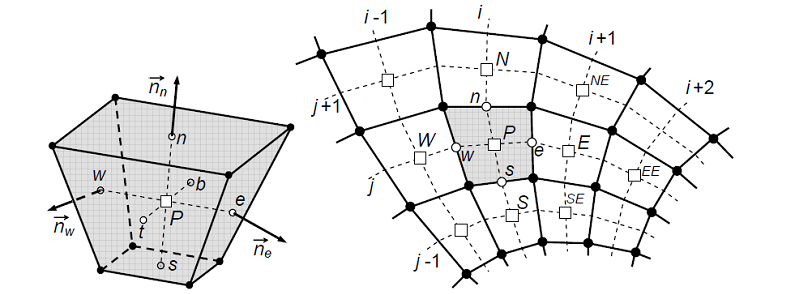
Дискретизация системы уравнения движения в данном вычислительном пакете OpenFOAM производиться по методу конечных объемов FVM (Finite-volume method). Локализация дискретных значений скорости и давления производится в центрах ячеек построенной расчетной сетки.
| Слагаемое | Схема аппроксимации в пакете OpenFOAM | Порядок аппроксимации |
| Производная по времени | Euler | Первый |
| Градиент давления | Gauss linear | Второй* |
| Конвективное слагаемое | Gauss limitedCubicV 0.2 | Первый/второй |
| Лапласиан | Gauss linear corrected | Второй* |
*- в некоторых областях, характеристики сетки могут снизить порядок точности.
Решение
Решение задачи производится при помощи утилиты icoFoam в основе которого лежит алгоритм PISO. Основные шаги представлены на схеме. Итерационная процедура основана на последовательном решении уравнений для скоростей и давления.

Для решения системы линейных уравнений для p был использован солвер PCG (предварительно сопряженных градиентов). Чтобы задать начальное приближение использовалась солвер GAMG (многосеточный метод с V циклом), со сглаживанием Гаусс-Зейделя. Для решения системы линейных уравнений для U было использовалась солвер PBiCG (предварительно бисопряженных градиентов), с солвером DILU (Diagonal incomplite-LU) для начальных приближений.
| Задача | Метод решения | Параметры |
| Для давления | PCG | preconditioner GAMG, tolerance 1e-6; relTol 0; |
| Предобуславливатель | GAMG | Smoother GaussSeidel; agglomerator faceAreaPair; mergeLevels 1; relTol 0; nCellsInCoarsestLevel 10;cacheAgglomeration true; |
| Для скоростей | PbiCG | solver PbiCG;preconditioner DILU; tolerance 1e-06; relTol 0; |
Preconditioner– предобуславливатель,
Tolerance – максимально допустимое значение модуля невязки,
Smoother – метод сглаживания,
Agglomerator –аггломератор,
nCellsInCoarsestLevel – число ячеек на самой грубой сетке.
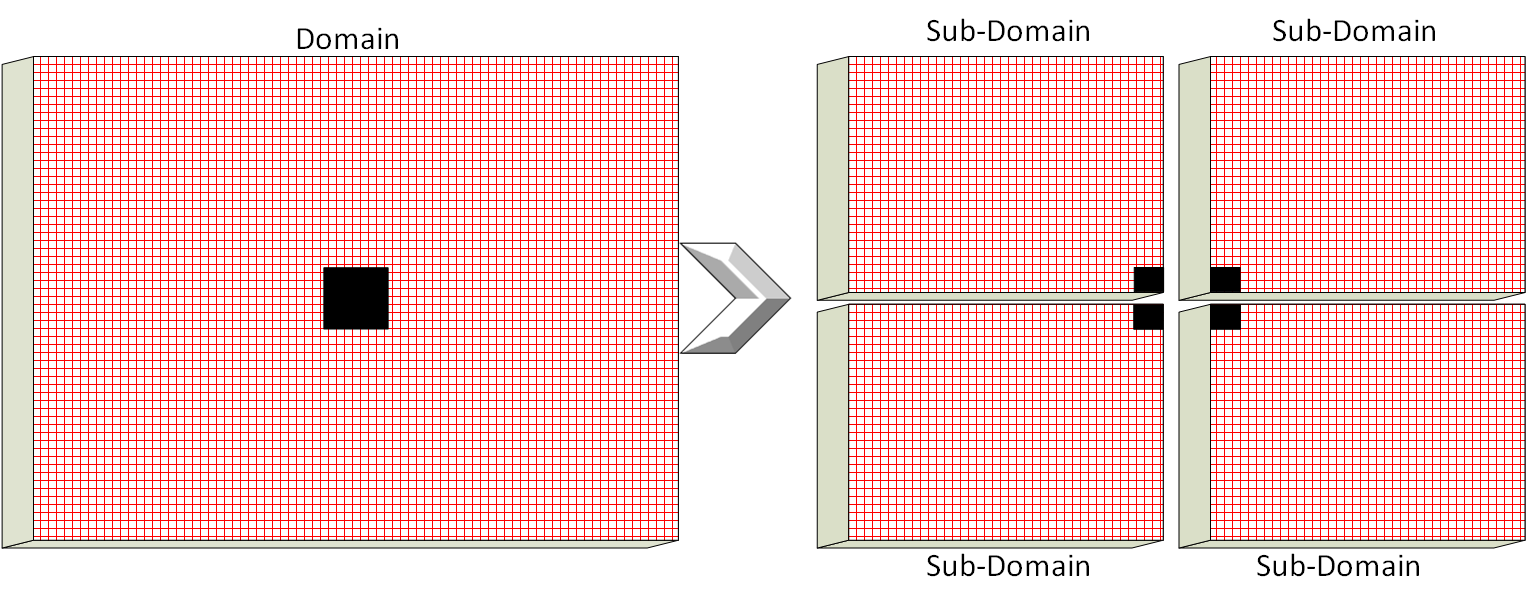
Применяется метод (domain decomposition) декомпозиции расчетной области. Область решения делится на 4 подобласти меньшего размера, которые рассчитываются на различных ядрах процессора.
Результаты
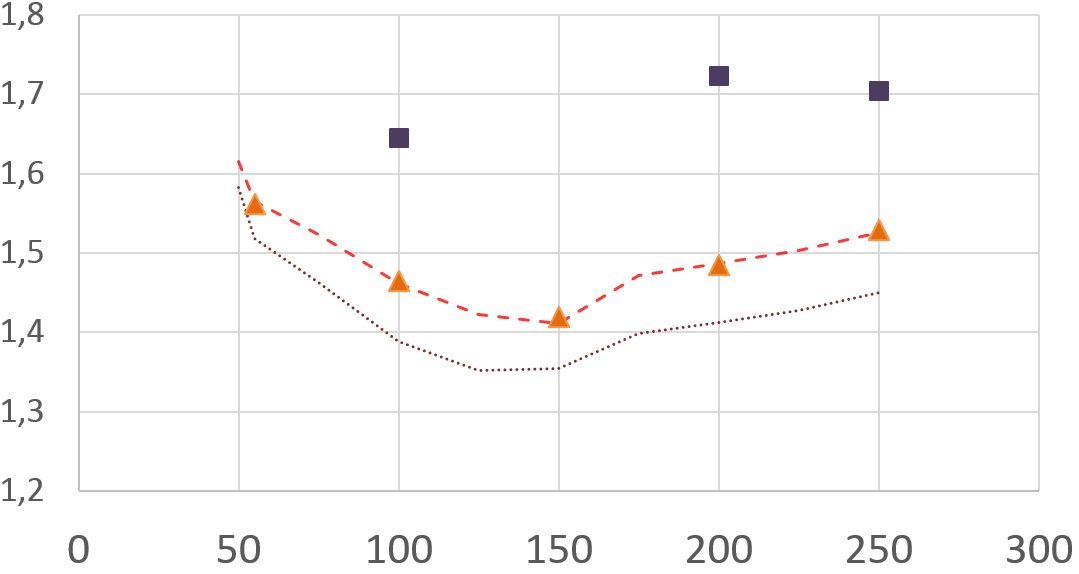
Зависимость Cd от числа Рейнольдса.
▲- OpenFOAM, ∎- Davis&Moore (1982) — - — - — Шушанта Дутта(2008) ∙∙∙∙∙ Гера (2010)
Наши результаты практически совпали с результатами других исследователей. Однако, для скошенных сеток результаты значительно отличны от экспериментальных.
Ну и красивая картинка обтекания.

Применение в других областях
Официальный сайт OpenFOAM
P.S. Первый мой пост на habrahabr