
Списки с пропусками — это структура данных, которая может применяться вместо сбалансированных деревьев. Благодаря тому, что алгоритм балансировки вероятностный, а не строгий, вставка и удаление элемента в списках с пропусками реализуется намного проще и значительно быстрее, чем в сбалансированных деревьях.
Списки с пропусками — это вероятностная альтернатива сбалансированным деревьям. Они балансируются с использованием генератора случайных чисел. Несмотря на то, что у списков с пропусками плохая производительность в худшем случае, не существует такой последовательности операций, при которой бы это происходило постоянно (примерно как в алгоритме быстрой сортировки со случайным выбором опорного элемента). Очень маловероятно, что эта структура данных значительно разбалансируется (например, для словаря размером более 250 элементов вероятность того, что поиск займёт в три раза больше ожидаемого времени, меньше одной миллионной).
Балансировать структуру данных вероятностно проще, чем явно обеспечивать баланс. Для многих задач списки пропуска это более естественное представление данных по сравнению с деревьями. Алгоритмы получаются более простыми для реализации и, на практике, более быстрыми по сравнению со сбалансированными деревьями. Кроме того, списки с пропусками очень эффективно используют память. Они могут быть реализованы так, чтобы на один элемент приходился в среднем примерно 1.33 указатель (или даже меньше) и не требуют хранения для каждого элемента дополнительной информации о балансе или приоритете.
Для поиска элемента в связном списке мы должны просмотреть каждый его узел:

Если список хранится отсортированным и каждый второй его узел дополнительно содержит указатель на два узла вперед, нам нужно просмотреть не более, чем ⌈n/2⌉ + 1 узлов(где n — длина списка):

Аналогично, если теперь каждый четвёртый узел содержит указатель на четыре узла вперёд, то потребуется просмотреть не более чем ⌈n/4⌉ + 2 узла:

Если каждый 2i-ый узел содержит указатель на 2i узлов вперёд, то количество узлов, которые необходимо просмотреть, сократится до ⌈log2 n⌉, а общее количество указателей в структуре лишь удвоится:

Такая структура данных может использоваться для быстрого поиска, но вставка и удаление узлов будут медленными.
Назовём узел, содержащий k указателей на впередистоящие элементы, узлом уровня k. Если каждый 2i-ый узел содержит указатель на 2i узлов вперёд, то уровни распределены так: 50% узлов — уровня 1, 25% — уровня 2, 12.5% — уровня 3 и т.д. Но что произойдёт, если уровни узлов будут выбираться случайно, в тех же самых пропорциях? Например, так:

Указатель номер i каждого узла будет ссылаться на следующий узел уровня i или больше, а не на ровно 2i-1 узлов вперёд, как было до этого. Вставки и удаления потребуют только локальных изменений; уровень узла, выбранный случайно при его вставке, никогда не будет меняться. При неудачном назначении уровней производительность может оказаться низкой, но мы покажем, что такие ситуации редки. Из-за того, что эти структуры данных представляют из себя связные списки с дополнительными указателями для пропуска промежуточных узлов, я называю их списками с пропусками.
Операции
Опишем алгоритмы для поиска, вставки и удаления элементов в словаре, реализованном на списках с пропусками. Операция поиска возвращает значение для заданного ключа или сигнализирует о том, что ключ не найден. Операция вставки связывает ключ с новым значением (и создаёт ключ, если его не было до этого). Операция удаления удаляет ключ. Также в эту структуру данных можно легко добавить дополнительные операции, такие как «поиск минимального ключа» или «нахождение следующего ключа».
Каждый элемент списка представляет из себя узел, уровень которого был выбран случайно при его создании, причём независимо от числа элементов, которые уже находились там. Узел уровня i содержит i указателей на различные элементы впереди, проиндексированные от 1 до i. Мы можем не хранить уровень узла в самом узле. Количество уровней ограничено заранее выбранной константой MaxLevel. Назовём уровнем списка максимальный уровень узла в этом списке (если список пуст, то уровень равен 1). Заголовок списка (на картинках он слева) содержит указатели на уровни с 1 по MaxLevel. Если элементов такого уровня ещё нет, то значение указателя — специальный элемент NIL.
Инициализация
Создадим элемент NIL, ключ которого больше любого ключа, который может когда-либо появиться в списке. Элемент NIL будет завершать все списки с пропусками. Уровень списка равен 1, а все указатели из заголовка ссылаются на NIL.
Поиск элемента
Начиная с указателя наивысшего уровня, двигаемся вперед по указателям до тех пор, пока они ссылаются на элемент, не превосходящий искомый. Затем спускаемся на один уровень ниже и снова двигаемся по тому же правилу. Если мы достигли уровня 1 и не можем идти дальше, то мы находимся как раз перед элементом, который ищем (если он там есть).
Search(list, searchKey)
x := list→header
# инвариант цикла: x→key < searchKey
for i := list→level downto 1 do
while x→forward[i]→key < searchKey do
x := x→forward[i]
# x→key < searchKey ≤ x→forward[1]→key
x := x→forward[1]
if x→key = searchKey then return x→value
else return failure
Вставка и удаление элемента
Для вставки или удаления узла применяем алгоритм поиска для нахождения всех элементов перед вставляемым (или удаляемым), затем обновляем соответствующие указатели:
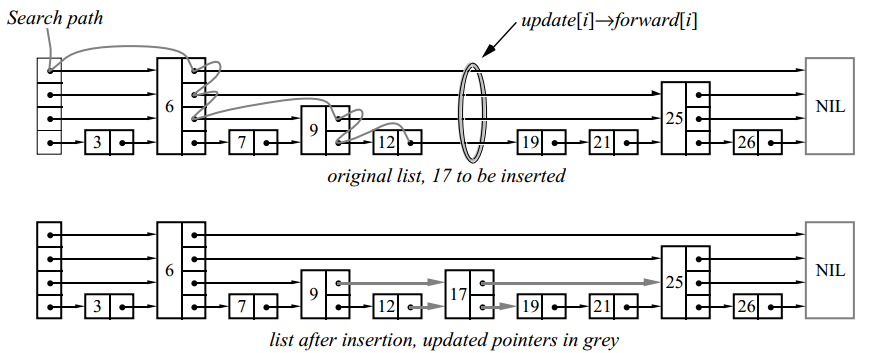
В данном примере мы вставили элемент уровня 2.
Insert(list, searchKey, newValue)
local update[1..MaxLevel]
x := list→header
for i := list→level downto 1 do
while x→forward[i]→key < searchKey do
x := x→forward[i]
# x→key < searchKey ≤ x→forward[i]→key
update[i] := x
x := x→forward[1]
if x→key = searchKey then x→value := newValue
else
lvl := randomLevel()
if lvl > list→level then
for i := list→level + 1 to lvl do
update[i] := list→header
list→level := lvl
x := makeNode(lvl, searchKey, value)
for i := 1 to level do
x→forward[i] := update[i]→forward[i]
update[i]→forward[i] := x
Delete(list, searchKey)
local update[1..MaxLevel]
x := list→header
for i := list→level downto 1 do
while x→forward[i]→key < searchKey do
x := x→forward[i]
update[i] := x
x := x→forward[1]
if x→key = searchKey then
for i := 1 to list→level do
if update[i]→forward[i] ≠ x then break
update[i]→forward[i] := x→forward[i]
free(x)
while list→level > 1 and list→header→forward[list→level] = NIL do
list→level := list→level – 1
Для запоминания элементов перед вставляемым(или удаляемым) используется массив update. Элемент update[i] — это указатель на самый правый узел, уровня i или выше, из числа находящихся слева от места обновления.
Если случайно выбранный уровень вставляемого узла оказался больше, чем уровень всего списка (т.е. если узлов с таким уровнем ещё не было), увеличиваем уровень списка и инициализируем соответствующие элементы массива update указателями на заголовок. После каждого удаления проверяем, удалили ли мы узел с максимальным уровнем и, если это так, уменьшаем уровень списка.
Генерация номера уровня
Ранее мы приводили распределение уровней узлов в случае, когда половина узлов, содержащих указатель уровня i, также содержали указатель на узел уровня i+1. Чтобы избавиться от магической константы 1/2, обозначим за p долю узлов уровня i, содержащих указатель на узлы уровня i+i. Номер уровня для новой вершины генерируется случайно по следующему алгоритму:
randomLevel()
lvl := 1
# random() возвращает случайное число в полуинтервале [0...1)
while random() < p and lvl < MaxLevel do
lvl := lvl + 1
return lvl
Как можно заметить, количество элементов в списке не участвует в генерации.
С какого уровня начинать искать? Определение L(n)
В списке с пропусками из 16 элементов, сгенерированном при p = 1/2, может получиться так, что в нем будет 9 элементов уровня 1, 3 элемента уровня 2, 3 элемента уровня 3 и 1 элемент уровня 14 (это маловероятно, но возможно). Как с этим быть? Если мы будем использовать стандартный алгоритм и искать, начиная с уровня 14, то проделаем много бесполезной работы.
Откуда лучше начинать поиск? Наши исследования показали, что лучше всего начинать поиск с уровня L, на котором мы ожидаем 1/p узлов. Это случится при L = log 1/p n. Для удобства дальнейших рассуждений обозначим функцию log 1/p n как L(n).
Есть несколько способов решения проблемы с узлами неожиданно большого уровня:
- Не париться (ориг. Don't worry, be happy). Просто начинать поиск с самого большого уровня, который есть в списке. Как мы увидим в дальнейшем, вероятность того, что уровень списка из n элементов окажется значительно выше чем L(n), очень мала. Такое решение добавляет лишь маленькую константу в ожидаемое время поиска. Этот подход использован в алгоритмах, приведённых выше.
- Использовать меньше места, чем нужно. Несмотря на то, что элемент может содержать 14 указателей, мы не обязательно должны использовать все 14. Мы можем использовать только L(n) из них. Есть несколько способов это реализовать, но все они усложняют алгоритм и не приводят к заметному увеличению производительности. Этот способ не рекомендуется к использованию.
- Починить кубик. Если сгенерировался уровень больший, чем максимальный уровень узла в списке, то просто считаем, что он больше ровно на 1. В теории и, похоже, на практике это работает хорошо. Но при таком подходе мы совершенно теряем возможность анализировать сложность алгоритмов, т.к. уровень узлов больше не полностью случаен. Программисты могут свободно использовать этот способ, но теоретикам лучше его избегать.
Выбор MaxLevel
Так как ожидаемое число уровней — L(n), лучше всего выбрать MaxLevel = L(N), где N — максимальное число элементов в списке с пропусками. Например, если p = 1/2, то MaxLevel = 16 подойдёт для списков, содержащих менее 216 элементов.
Анализ алгоритмов
В операциях поиска, вставки и удаления больше всего времени уходит на поиск подходящего элемента. Для вставки и удаления дополнительно нужно время, пропорциональное уровню вставляемого или удаляемого узла. Время поиска элемента пропорционально количеству пройденных в процессе поиска узлов, которое, в свою очередь, зависит от распределения их уровней.
Вероятностная философия
Структура списка с пропусками определяется только количеством элементов в этом списке и значениями генератора случайных чисел. Последовательность операций, с помощью которых получен список, не важна. Мы предполагаем, что у пользователя нет доступа к уровням узлов, иначе, он может сделать так, чтобы алгоритм работал за наихудшее время, удалив все узлы, уровень которых отличен от 1.
Для последовательных операций на одной структуре данных времена их выполнения не являются независимыми случайными величинами; две последовательных операции поиска одного и того же элемента займут в точности одно и то же время.
Анализ ожидаемого времени поиска
Рассмотрим пройденный при поиске путь с конца, т.е. будем двигаться вверх и влево. Хотя уровни узлов в списке известны и зафиксированы на момент поиска, мы предположим, что уровень узла определяется только когда мы встретили его при движении с конца.
В любой заданной точке пути мы находимся в такой ситуации:

Мы смотрим на i-ый указатель узла x и не знаем об уровнях узлов слева от x. Также мы не знаем точного уровня x, но он должен быть как минимум i. Предположим, что x — это не заголовок списка (это эквивалентно предположению, что список бесконечно расширяется влево). Если уровень x равен i, то мы находимся в ситуации b. Если уровень x больше i, то мы в ситуации c. Вероятность того, что мы находимся в ситуации c, равна p. Каждый раз, когда это происходит, мы поднимаемся вверх на один уровень. Пусть C(k) — это ожидаемая длина обратного пути поиска, при котором мы двигались вверх k раз:
C(0) = 0
C(k) = (1-p) (длина пути в ситуации b) + p (длина пути в ситуации c)
Упрощаем:
C(k) = (1-p)(1 + C(k)) + p⋅(1 + C(k-1))
C(k) = 1 + C(k) — p⋅C(k) + p ⋅ C(k-1)
C(k) = 1/p + C(k — 1)
C(k) = k/p
Наше предположение о том, что список бесконечный — пессимистично. Когда мы доходим до самого левого элемента, мы просто двигаемся все время вверх, не двигаясь влево. Это даёт нам верхнюю границу (L(n) — 1) /p ожидаемой длины пути от узла с уровнем 1 до узла с уровнем L(n) в списке из n элементов.
Мы используем эти рассуждения, чтобы добраться до узла уровня L(n), но для остальной части пути используются другие рассуждения. Количество оставшихся ходов влево ограничено числом узлов, имеющих уровень L(n), или выше во всем списке. Наиболее вероятное число таких узлов 1/p.
Мы также двигаемся вверх от уровня L(n) до максимального уровня в списке. Вероятность того, что максимальный уровень списка больше k, равна 1-(1-pk)n, что не больше, чем npk. Мы можем вычислить, что ожидаемый максимальный уровень не более L(n) + 1/(1-p). Собирая всё вместе, получим, что ожидаемая длина пути поиска для списка из n элементов
<=L(n)/p + 1/(1-p),
или O(log n).
Количество сравнений
Мы только что посчитали длину пути, проходимого при поиске. Требуемое число сравнений на единицу больше длины пути (сравнение происходит на каждом шаге пути).
Вероятностный анализ
Мы можем рассмотреть распределение вероятностей различных длин путей поиска. Вероятностный анализ в некоторой степени более сложный (он есть в самом конце оригинальной статьи). С его помощью мы можем оценить сверху вероятность того, что длина пути поиска превысит ожидаемую более чем в заданное число раз. Результаты анализа:
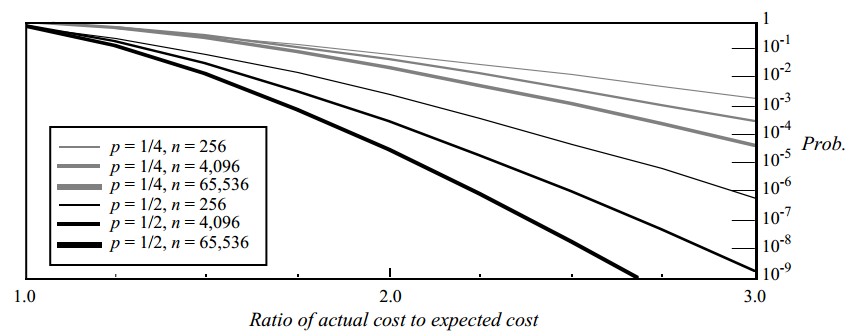
Здесь изображён график верхней границы вероятности того, что операция займет значительно больше времени, чем ожидалось. На вертикальной оси отложена вероятность того, что длина пути поиска окажется больше ожидаемой длины пути в количество раз, отложенное на горизонтальной оси. Например, при p = 1/2 и n = 4096, вероятность того, что получившийся путь окажется в три раза длиннее, чем ожидаемый, меньше 1 / 200 000 000.
Выбор p
В таблице приведены нормализованные времена поиска и объем требуемой памяти для различных значений p:
| p | Нормализованное время поиска (т.e. нормализованное L(n)/p ) |
Среднее количество указателей на узел (т.е. 1/(1 – p) ) |
|---|---|---|
| 1/2 | 1 | 2 |
| 1/e | 0.94... | 1.58... |
| 1/4 | 1 | 1.33... |
| 1/8 | 1.33... | 1.14... |
| 1/16 | 2 | 1.07... |
Уменьшение p увеличивает разброс времени операций. Если 1/p является степенью двойки, то удобно генерировать номер уровня из потока случайных бит (для генерации в среднем требуется (log2 1/p)/(1-p) случайных бит). Так как существуют накладные расходы, относящиеся к L(n) (но не к L(n)/p), то выбор p=1/4 (вместо 1/2) слегка уменьшает константу в сложности алгоритма. Рекомендуем выбирать p=1/4, но если разброс времени операций для вас важнее скорости, то выбирайте 1/2.
Несколько операций
Ожидаемое итоговое время последовательности операций равняется сумме ожидаемых времён для каждой операции в последовательности. Таким образом, ожидаемое время для любой последовательности m операций поиска в структуре данных из n элементов равняется O(m * log n). Однако, характер (pattern) операций поиска влияет на распределение фактического времени всей последовательности операций.
Если мы ищем один и тот же элемент в одной и той же структуре данных, то обе операции займут в точности одно и то же время. Таким образом, дисперсия (разброс) итогового времени будет в четыре раза больше дисперсии одной операции поиска. Если времена поиска двух элементов — независимые случайные величины, то дисперсия общего времени равна сумме дисперсий времён выполнения отдельных операций. Поиск одного и того же элемента снова и снова максимизирует дисперсию.
Тесты производительности
Сравним производительность списков с пропусками с другими структурами данных. Все реализации были оптимизированы для достижения максимальной производительности:
| Структура данных | Поиск | Вставка | Удаление |
|---|---|---|---|
| списки с пропусками | 0.051 мсек (1.0) | 0.065 мсек (1.0) | 0.059 мсек (1.0) |
| нерекурсивные AVL деревья | 0.046 мсек (0.91) | 0.10 мсек (1.55) | 0.085 мсек (1.46) |
| рекурсивные 2–3 деревья | 0.054 мсек (1.05) | 0.21 мсек (3.2) | 0.21 мсек (3.65) |
| Саморегулирующиеся деревья: | |||
| расширяющиеся сверху вниз (top-down splaying) | 0.15 мсек (3.0) | 0.16 мсек (2.5) | 0.18 мсек (3.1) |
| расширяющиеся снизу вверх (bottom-up splaying) | 0.49 мсек (9.6) | 0.51 мсек (7.8) | 0.53 мсек (9.0) |
Тесты выполнялись на машине Sun-3/60 и производились на структурах данных, содержащих 216 элементов. Значения в скобках — время, относительно списков с пропусками (в разах). Для тестов вставки и удаления элементов не учитывалось время, затрачиваемое на управление памятью (например, на C-шные вызовы malloc и free).
Заметим, что списки с пропусками требуют больше операций сравнения, чем другие структуры данных (алгоритмы, приведённые выше, требуют в среднем L(n)/p + 1/(1 + p) операций). При использовании вещественных чисел в качестве ключей, операции в списках с пропусками оказались немного медленнее, чем в нерекурсивной реализации AVL-дерева, а поиск в списках с пропусками оказался немного медленнее, чем поиск в 2-3 дереве (тем не менее, вставка и удаление в списках с пропусками были быстрее, чем в рекурсивной реализации 2-3 деревьев). Если операции сравнения очень дорогие, можно модифицировать алгоритм так, что искомый ключ не будет сравниваться с ключом других узлов более одного раза на узел. При p = 1/2 верхняя граница количества сравнений равна 7/2 + 3/2 * log2 n.
Неравномерное распределение запросов
Саморегулирующиеся деревья могут адаптироваться к неравномерному распределению запросов. Так как списки с пропусками быстрее саморегулирующихся деревьев в довольно большое число раз, саморегулирующиеся деревья оказываются быстрее только при некоторых очень неравномерных распределениях запросов. Мы могли бы попытаться разработать саморегулирующиеся списки с пропусками, однако, не видели в этом практического смысла и не хотели портить простоту и производительность оригинальной реализации. Если в приложении ожидаются неравномерные запросы, то использование саморегулирующихся деревьев или добавление кэширования будут более предпочтительными.
Заключение
С теоретической точки зрения, списки с пропусками не нужны. Сбалансированные деревья могут делать те же операции и имеют хорошую сложность в худшем случае (в отличие от списков с пропусками). Однако, реализация сбалансированных деревьев — сложная задача и, как следствие, они редко реализуются на практике, кроме как в качестве лабораторных работ в университетах.
Списки с пропусками — это простая структура данных, которая может использоваться вместо сбалансированных деревьев в большинстве случаев. Алгоритмы очень легко реализовывать, расширять и изменять. Обычные реализации операций на списках с пропусками примерно такие же быстрые, как высокооптимизированные реализации на сбалансированных деревьях и в значительной степени быстрее обычных, невысокооптимизированных реализаций.






