
Запятошка: Устраивайся поудобнее, Жучок, мы будем с тобой сегодня проводить мысленные эксперименты со свободно падающими телами.
Жучок: А это как? Тела будут падать в моём воображении? Прямо так и вижу: обнажённые тела, летящие на фоне звёздного неба…
Запятошка: Тела, конечно, воображаемые, но не настолько большие, чтобы быть обнажёнными. Вообще, речь пойдёт о свободном падении тел в однородном гравитационном поле.

Жучок: Что это ещё за проектор снов такой?
Запятошка: Это мой экспериментальный проект. Пока что это куча страшного кода на Python с использованием IPython для связки. Ну, да вернёмся к нашему разговору. Итак, тело, падающее свободно с начальной скоростью
 движется с ускорением…
движется с ускорением…Жучок: Опять ты бубнишь себе под нос всякие непонятные проклятия. Я много раз видел, как летят кусочки бабочек, которых с удовольствием пожираю каждый день. А твой проектор может показать, что получится, если разбросать кучу ошмётков места в разные стороны? Я тут подумываю о новом способе потрошения бабо… прости, поглощения обеда.
Запятошка: Вечно ты о еде думаешь, Жучок. А вообще, да, мы можем такую ситуацию смоделировать. Давай предположим, что все кусочки вылетают из одного с одинаковой скоростью, и проследим их полёт в течении первых нескольких секунд.

Жучок: Ого, салют!
Запятошка: Правда, похоже? А ещё что-нибудь замечаешь?
Жучок: Хм-м, похоже, что кусочки образуют круг… всегда… любопытная картинка. А почему так происходит?
Запятошка: Прежде, чем я объясню, заметь, что ты опознал, что это круг без всяких вычислений и формул. Даже в проекторе, если посмотришь, нигде нет указания, что кусочки должны всегда образовывать круг. Я просто указала проектору сэмулировать много летящих кусочков и всё, а уже твой мозг сам заметил закономерность безо всяких заумных объяснений и формул. Главное, задать интересный вопрос и иметь под рукой такой вот проектор!
А теперь попробую объяснить, почему получается такая картинка. Представь, что ты — один из маленьких кусочков, летящих вместе с остальными. Однако, тебя не швырнули вместе со всеми, тебе удалось ускользнуть и ты выпал из гнезда без начальной скорости. Немного придя в себя ты начинаешь смотреть вокруг и наблюдать за остальными кусочками. Как, по-твоему, на что будет похоже их поведение?
Жучок: Ну, они наверное будут от меня удаляться, так как их-то вышвырнули из гнезда.
Запятошка: Всё верно, в системе отсчёта, связанной с тобой падающим свободно, не будет действовать сила притяжения, а значит, что кусочки будут от тебя удаляться, двигаясь с одинаковой скорость равномерно и прямолинейно.
Жучок: Ух, как ты опять начала умничать. Но суть я уловил: кусочки будут от меня убегать как по спицам велосипеда, и в целом будут образовывать круг как велосипедное колесо. А это можно «увидеть» в твоём проекторе?
Запятошка: Можно, и это тебе будет упражнением на дом. А ещё попробуй доказать формально, что кусочки будут всегда образовывать круг, используя формулы для свободного падения.
Жучок: Ладно, ладно. А что ещё интересного можно посмотреть в твоём проекторе?
Запятошка: Я тебе расскажу про один приём нахождения любопытных свойств у обычных явлений. Ты ведь помнишь, что свободно падающие тела движутся, в общем случае, по параболе?
Жучок: Так вот что у тебя там рисуется как хвост у звёздочек в проекторе! Да, что-то у меня про параболы осталось в памяти.
Зпятошка: Очень хорошо! Давай посмотрим в энциклопедии какими интересными свойствами обладает парабола. Для начала, посмотрим какая получится картинка, если пометить вершины траекторий кусочков, полётом которых мы любовались выше.
Жучок: А как ты объяснишь проектору в каком месте ставить метку?
Запятошка: Ну, мы можем это сделать двумя способами. Если бы мы исследовали неизвестный феномен, то можно было бы просто объяснить проектору как найти локальный максимум траектории. Но мы-то знаем как движется тело в поле земли, поэтому попробуем подобрать формулу для координат вершины, и одновременно посмотрим как нам в этом может помочь пакет sympy, который умеет решать всевозможные задачки в символьном виде.
Инициализация
import numpy as np
from IPython.core.display import Image
from sympy import *
init_printing()
x,y,z = symbols('x y z')
v_0, alpha, g, t = symbols('v_0, alpha, g, t', real=True)
v_x = v_0 * cos(alpha)
v_y = v_0 * sin(alpha) - g * t
(Eq(Symbol('v_x'), v_x), Eq(Symbol('v_y'), v_y))

Запятошка: теперь вычислим координаты кусочка, учитывая, что запустили мы его из точки (0,0). Для этого необходимо проинтегрировать скорость по времени
x_t = integrate(v_x, t)
y_t = integrate(v_y, t)
(Eq(x, x_t),Eq(y, y_t))
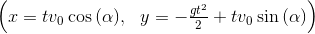
Жучок: постой, постой! Я запутался немного. Почему ты пишешь Symbol('v_x')? Почему нельзя просто указать переменную v_x, чтобы увидеть результирующее уравнение? Да и сами уравнения ты как-то странно выводишь…
Запятошка: ты очень наблюдательный, Жучок, молодец! Это потому, что переменная v_х и символ v_х — это разные сущности. Подробнее можешь почитать вот здесь.
Запятошка: На вершине траектории вертикальная скорость
 , откуда находим момент времени
, откуда находим момент времени 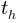 когда это происходит.
когда это происходит.solution=solve(v_y, t)
t_h = solution[0]; t_h

Запятошка: Наконец, координаты вершины параболы:
x_h = x_t.subs(t, t_h);x_h
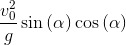
y_h = y_t.subs(t, t_h);y_h
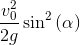
Запятошка: Обучаем наш проектор этому знанию и смотрим что получается.

Жучок: Обалдеть! Это же… это же… Эллипс! Ну очень похож!
Запятошка: Молодец, Жучок. Заметь, ты сначала увидел картинку, а мозг уже сам подсказал тебе закономерность, которую нельзя было заметить сколь бы мы ни пялились на формулы.
Жучок: Запятошка, я кажется начинаю понимать зачем ты возишься со своим проектором. А мы будем доказывать, что это реально эллипс, а не фикция нашего воображения?
Запятошка: Конечно, давай попробуем это сделать. Правда, нам придётся немного попотеть объясняя sympy чего мы хотим добиться. По сути, необходимо избавиться от угла в выражениях для вершин парабол, и получить формулу, связывающую
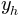 и
и  . Если попробовать решить в лоб:
. Если попробовать решить в лоб:solve([x-x_h, y-y_h], [y, alpha])
Запятошка: то получится абракадабра (проверь дома сам). А всё потому, что sympy ещё маленький, не умеет элегантно манипулировать тригонометрическими выражениями. Но мы ему поможем. Для начала:
x_h = trigsimp(x_h); x_h
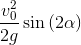
Запятошка: далее заметим, что в выражении для
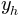 можно сделать замену
можно сделать замену 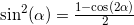 . Делаем подстановку и получаем:
. Делаем подстановку и получаем:y_h = y_h.subs(sin(alpha)**2, (1-cos(2*alpha))/2);y_h
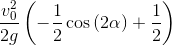
Жучок: Что-то мне подсказывает, что ты хочешь воспользоваться равенством
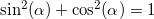
Запятошка: Сразу видно, что долгие ночи подготовки не прошли для тебя даром. Выражаем
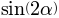 и
и  через
через  и
и  .
.s = solve([x-x_h, y-y_h], [sin(2*alpha), cos(2*alpha)]);s
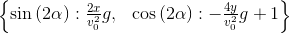
Запятошка: и подставляем в подмеченное тобой равенство:
Eq(s[sin(2*alpha)]**2 + s[cos(2*alpha)]**2, 1)
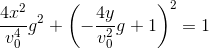
Запятошка: Получаем ни что иное, как уравнение эллипса!
Жучок: М-да…
Запятошка: Вот тебе ещё одно домашнее задание: выясни, как меняется форма эллипса в зависимости от начальной скорости, а также координаты его центра, можешь ещё и фокусы исследовать. Подсказка: найди эксцентриситет эллипса. Он, как ты помнишь, определяет форму эллипса
Жучок: Ладно-ладно, не ты одна такая умная, разберусь как-нибудь. Ты лучше ещё что-нибудь покажи, а то нашла какой-то эллипс и радуешься как ребёнок…
Запятошка: А вот и покажу! Читаем упомянутую выше энциклопедию дальше и обнаруживаем там описание фокуса параболы. Какой у нас сразу возникает вопрос? По твоей кислой мине сразу понятно, что мы хотим пометить фокусы всех наших парабол и посмотреть, что получится.
Жучок: Что, опять эллипс?
Запятошка: Почём мне знать? Давай посмотрим. В виду симметрии, абсцисса фокуса совпадает с абсциссой вершины параболы. А вот ординату надо будет найти по формуле
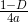 согласно энциклопедии. Для этого найдём сначала уравнение параболы через
согласно энциклопедии. Для этого найдём сначала уравнение параболы через  и
и  , избавишься для этого от
, избавишься для этого от 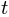 .
.ss = solve([x-x_t,y-y_t], [y,t], dict=True);ss

Запятошка: Следовательно, коэффициенты квадратичного трёхчлена:
a,b,c = ss[0][y].as_poly(x).all_coeffs(); a,b,c
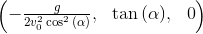
Запятошка: Дальше попробуй сам.
Жучок: Хорошо, значит дискриминант получится вот таким:
D = b**2 - 4*a*c; D
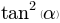
Жучок: и ордината фокуса:
y_f=(1-D)/(4*a);y_f
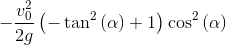
Жучок: Что получится, если это подставить в твой проектор, Запятошка?
Запятошка: А вот что!

Жучок: У меня нет слов! Чем-то смахивает на какой-то сакральный знак… Вспомнил! Око Ра!
Запятошка: Ну у тебя и воображение, Жучок. Попробуешь доказать, что фокусы ложатся на круг?
Жучок: Так, значит сначала пробуем упростить:
y_f = trigsimp(y_f); y_f
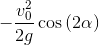
Жучок: Э, да тут всё просто получается! Даже потеть не надо, просто складываем квадраты абсциссы и ординаты:
Eq(x**2 + y**2, simplify(x_h**2 + y_f**2))
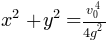
Запятошка: Ну, раз уж ты у нас такой молодец, то вот тебе ещё одна задачка на дом. Изучи, как ведут себя директрисы наших парабол.
Жучок: А что если у меня возникнут трудности?
Запятошка: Постарайся самостоятельно разобраться, помня, что наши инструменты всё ещё далеки от совершенства и им нужно эпизодически помогать и подсказывать. Если всё же вопросы останутся — встретимся ещё раз и пообщаемся.
Напоследок, последняя задачка: посмотри внимательно на самую первую картинку в начале нашей беседы — видишь, там ещё одна фигура на фоне вырисовывается? Попробуй выяснить, что это за фигура и как себя ведёт.
Вот тебе ещё парочка ресурсов для вдохновения.
- J. L. Fernandez-Chapou et al., An elliptic property of parabolic trajectories
- «Проектор снов»: исходный код
- Bret Victor, Up and Down the Ladder of Abstraction
- Bret Victor, Simulation as a Practical Tool






