В первой части статьи я писал о статистической обработке данных по ценам на товары за более чем 30 лет.
Здесь я попробую отследить взаимосвязи между отдельными товарами.
Если быть более точным, под катом немного matlab-кода и изображения графов.
Для начала подгружаем данные и вычисляем относительные цены (подробнее об этом в первой части статьи):
Далее вычисляем матрицу корреляционных коэффициентов:
Теперь можно строить граф:
При пороге корреляции равном 25% видим довольно сложную систему взаимосвязей:
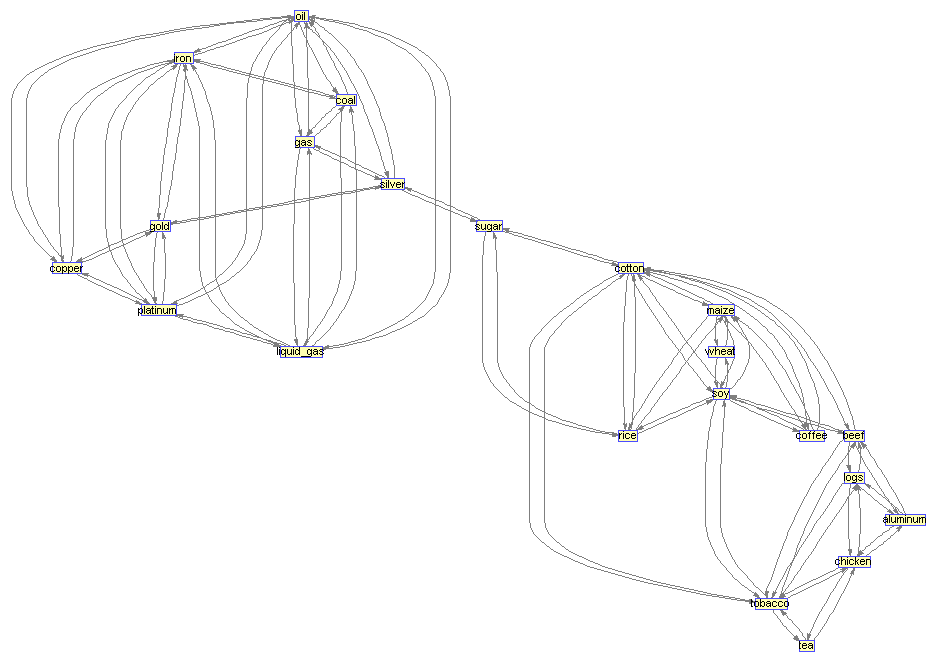
При пороге в 33% товары распадаются на 2 большие группы:
1. Нефть, уголь, газ, сжиженный газ, железная руда, платина, золото, серебро и медь.
2. Алюминий, бревна, куриное мясо, чай, табак, хлопок, кофе, рис, сахар, говядина, кукуруза, пшеница и соя.
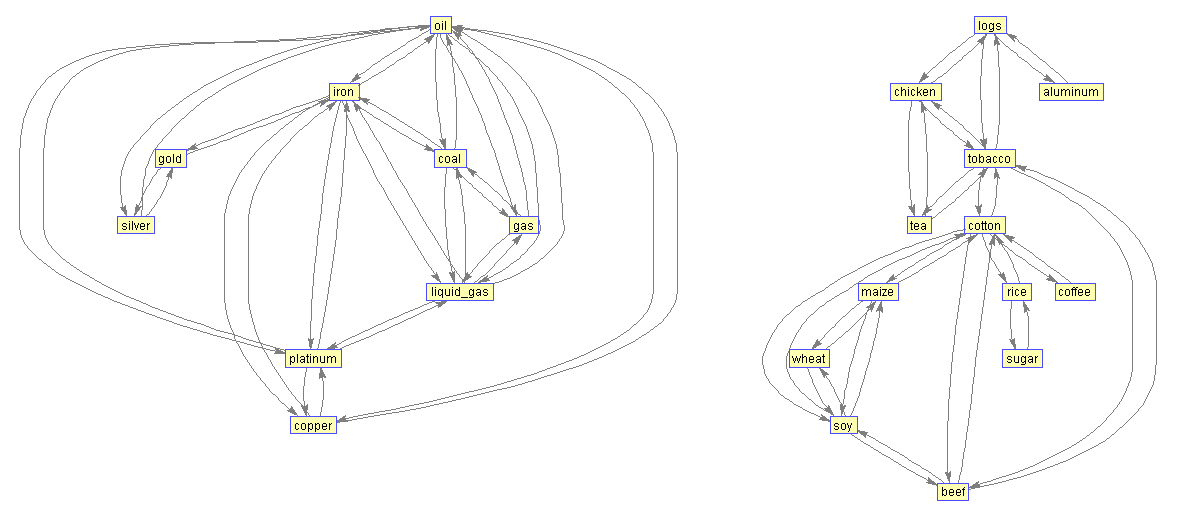
При корреляции более 40% групп становится больше:
1. Топливо (газ, сжиженный газ, уголь, нефть), а так же железная руда, платина и медь.
2. Бревна, куриное мясо, чай, табак, говядина, хлопок, кофе, кукуруза, пшеница и соя.
3. Золото и серебро.
4. Сахар и рис.
5. Алюминий — сам по себе.

При пороге в 45% выпадают из системы связей сахар, рис, кофе и уголь:

Порог 50%. Одна из групп распадается на две:
1. Бревна, курица, табак, говядина и чай.
2. Кукуруза, соя и пшеница.

Корреляция более 55% — по прежнему держится группа из газа, сжиженного газа, нефти, железа, меди и платина.
Распадается связь между золотом и серебром.
Связаны так же: бревна с курицей и табаком, кукуруза с соей.

Порог в 60%:
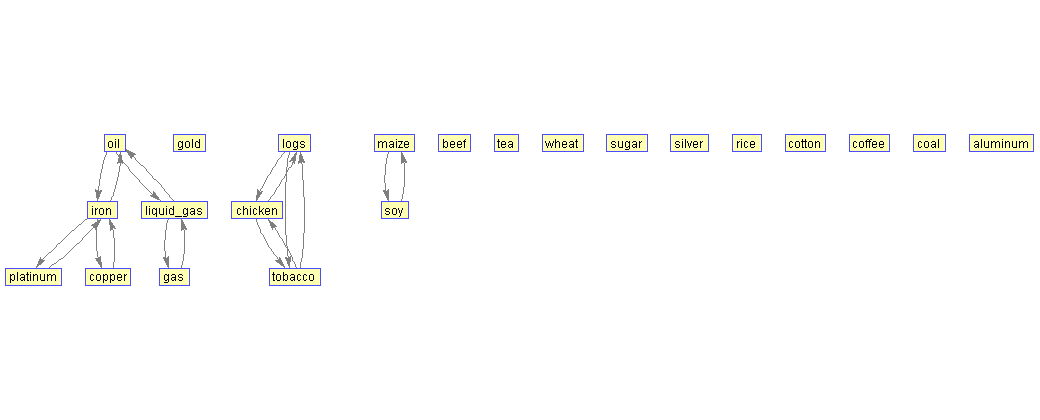
65%. Связанными остаются лишь 3 группы:
1. Газ, сжиженный газ и нефть.
2. Железная руда и медь.
3. Бревна и курица.

И, наконец, 70%.
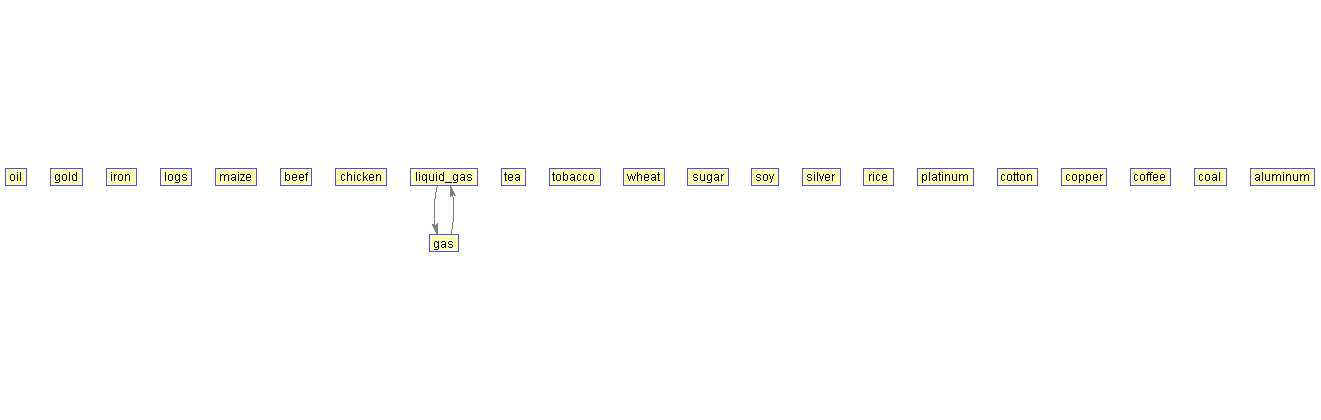
Связанными остаются лишь цены на газ и сжиженный газ:

Здесь я попробую отследить взаимосвязи между отдельными товарами.
Если быть более точным, под катом немного matlab-кода и изображения графов.
Для начала подгружаем данные и вычисляем относительные цены (подробнее об этом в первой части статьи):
xls = xlsread('data.xls');
time = 1:399;
data = xls(time,1:22);
oil = data(:,1);
gold = data(:,2);
iron = data(:,3);
logs = data(:,4);
% и остальные товары
all_goods = [oil gold iron logs maize beef chicken gas liquid_gas tea tobacco wheat sugar soy silver rice platinum cotton copper coffee coal aluminum];
% Наименования товаров, они понадобятся для построения графов:
ids = {'oil','gold','iron','logs','maize','beef','chicken','liquid_gas','gas','tea','tobacco','wheat','sugar','soy','silver','rice','platinum','cotton','copper','coffee','coal','aluminum'};
goods_count = size(all_goods, 2);
geom_average = ones(size(time))'; %'
for i = 1:goods_count
geom_average = geom_average .* all_goods(:,i);
end
geom_average = geom_average .^ (1/goods_count);
all_goods_rel = zeros(size(all_goods));
for i = 1:goods_count
all_goods_rel(:,i) = all_goods(:,i) ./ geom_average;
end
Далее вычисляем матрицу корреляционных коэффициентов:
R = corrcoef(all_goods_rel);
Теперь можно строить граф:
% порог корреляции:
threshold = 0.25; % 0.33 0.4 0.45 0.55 0.6 0.65 0.7
% матрица связей графа:
links = R>threshold;
% собственно, построение графа:
bg = biograph(links, ids);
view(bg);
Результаты
При пороге корреляции равном 25% видим довольно сложную систему взаимосвязей:
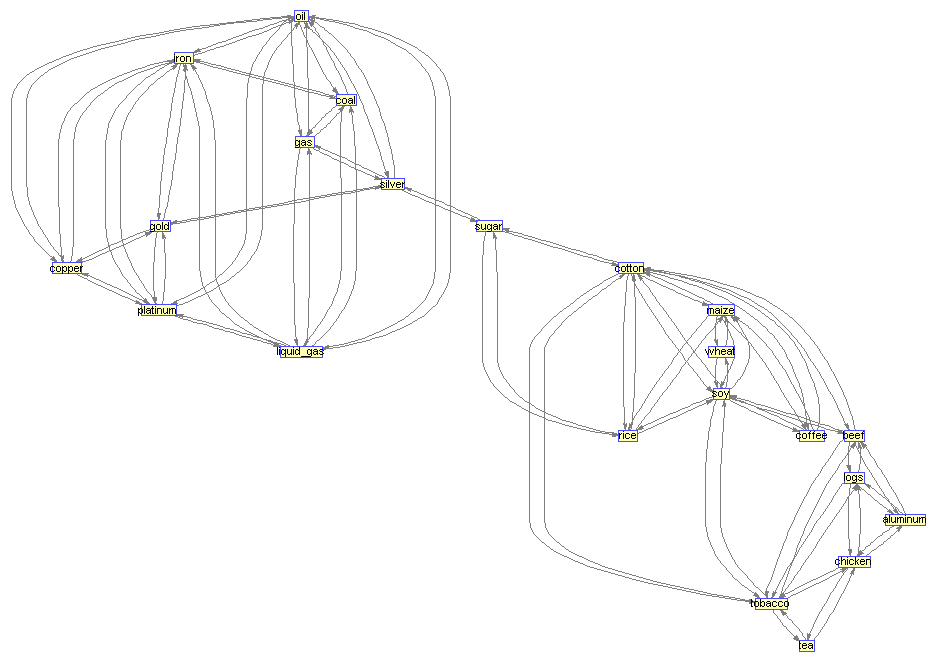
При пороге в 33% товары распадаются на 2 большие группы:
1. Нефть, уголь, газ, сжиженный газ, железная руда, платина, золото, серебро и медь.
2. Алюминий, бревна, куриное мясо, чай, табак, хлопок, кофе, рис, сахар, говядина, кукуруза, пшеница и соя.
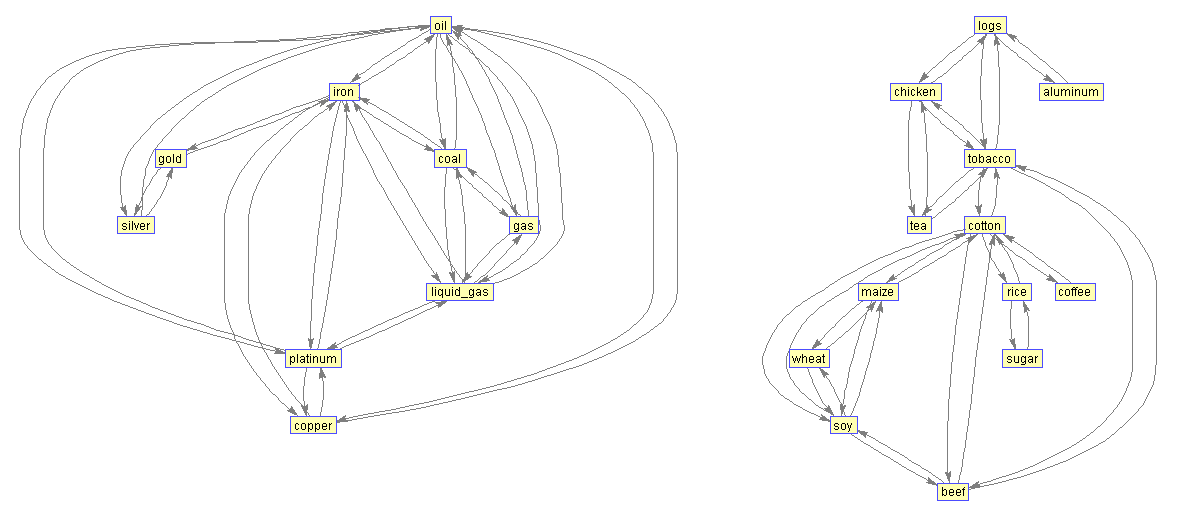
При корреляции более 40% групп становится больше:
1. Топливо (газ, сжиженный газ, уголь, нефть), а так же железная руда, платина и медь.
2. Бревна, куриное мясо, чай, табак, говядина, хлопок, кофе, кукуруза, пшеница и соя.
3. Золото и серебро.
4. Сахар и рис.
5. Алюминий — сам по себе.
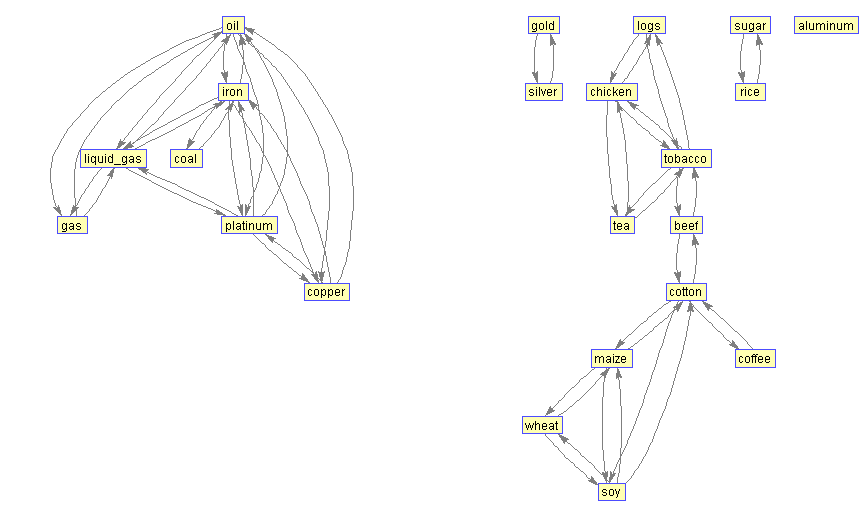
При пороге в 45% выпадают из системы связей сахар, рис, кофе и уголь:
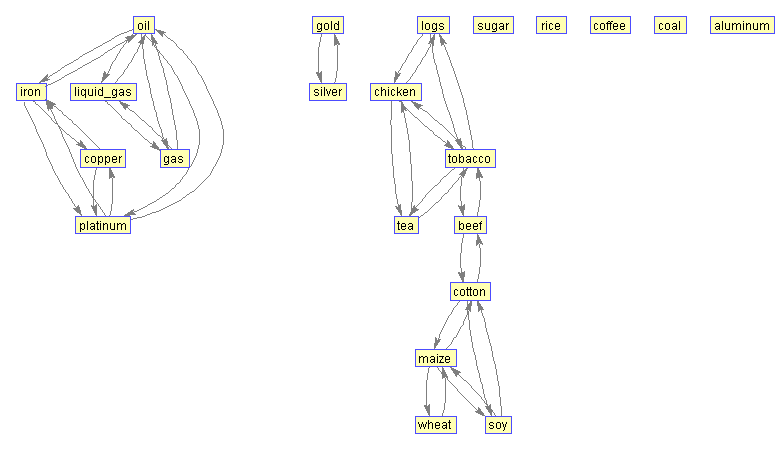
Порог 50%. Одна из групп распадается на две:
1. Бревна, курица, табак, говядина и чай.
2. Кукуруза, соя и пшеница.

Корреляция более 55% — по прежнему держится группа из газа, сжиженного газа, нефти, железа, меди и платина.
Распадается связь между золотом и серебром.
Связаны так же: бревна с курицей и табаком, кукуруза с соей.
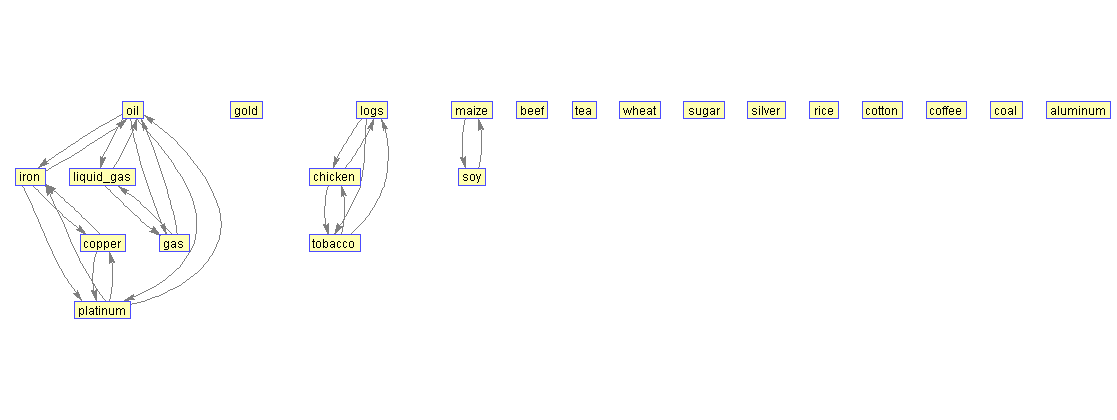
Порог в 60%:
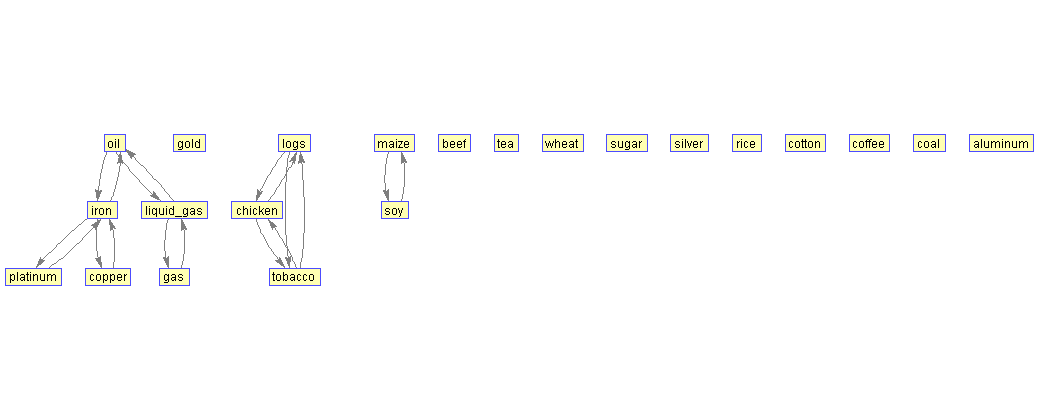
65%. Связанными остаются лишь 3 группы:
1. Газ, сжиженный газ и нефть.
2. Железная руда и медь.
3. Бревна и курица.

И, наконец, 70%.
Связанными остаются лишь цены на газ и сжиженный газ: