Quotient filter — это вероятностная структура данных, позволяющая проверить принадлежность элемента множеству. Она описана в 2011 г. как замена фильтру Блума. Ответ может быть:
— элемент точно не принадлежит множеству;
— элемент возможно принадлежит множеству.
В структуре хранятся хэши элементов, которые принадлежат множеству S:
F = h(S) = {h(x) | x in S}
Именно поэтому структура вероятностная.
Допустим, мы ищем элемент A. Вычисляем его хэш и ищем в структуре.
Ситуация 1: хэш элемента не был найден. Ответ — элемент точно не принадлежит множеству.
Ситуация 2: при поиске найден хэш, но нельзя сказать точно, принадлежит ли он элементу A. Иногда бывает, что хэши двух разных элементов совпадают(это совпадение называется полной коллизией — hard collision). Поэтому нельзя сказать точно, нашли ли мы хэш элемента A или это была коллизия. Ответ — элемент возможно принадлежит множеству.
Фильтр можно представить в виде хэш-таблицы T с m = 2 ^ q группами хэшей. Для распределения хэшей по группам используется метод «quotienting»(отсюда и название фильтра). Метод был предложен Кнутом(The Art of Computer Programming:Searching and Sorting, volume 3. Section 6.4, exercise 13).
Хэш разбивается на 2 части:
частное(quotient) fq = f / (2 ^ r)
остаток(remainder) fr = f mod (2 ^ r)
В итоге добавление хэша f в фильтр сводится к добавлению части fr в группу T[fq]. Полный хэш восстанавливается по формуле:
f = fq * (2 ^ r) + fr.
Формула(взята из [2])

Таблица T хранится в виде массива A[0..m — 1] элементов с длиной (r + 3) бита. Каждый слот массива хранит остаток от хэша и 3 бита информации, необходимой для восстановления хэша.
Если у 2 хэшей совпадают частные, то это называется мягкой коллизией(soft collision). Все хэши, у которых совпадают частные, хранятся в массиве последовательно в отрезке(run). При этом всегда выполняется условие: если fq1 < fq2, то fr1 находится в массиве всегда перед fr2.
Давайте разберемся, что делают дополнительные 3 бита, хранящиеся с каждым остатком.
1. бит занятости(is occupied). Если у слота i стоит этот бит, то в массиве есть хэш, у которого частное fq = i(но оно может быть не в этом слоте, а смещено дальше).
2. бит продолжения(is continuation). Если у слота i стоит этот бит, то хранящийся в нем остаток принадлежит тому же отрезку, что и остаток, хранящийся в предыдущем слоте i — 1.
3. бит смещения(is shifted). Если он выставлен, это значит, что хранящийся в слоте i остаток не принадлежит группе i, а просто был смещен.
Если бит смещения = 0, то в слоте i хранится остаток, принадлежащий этому слоту(fq = i). Бит продолжения позволяет понять, когда заканчивается отрезок. Бит занятости позволяет определить слот, которому принадлежит отрезок.
Хорошо описаны комбинации в Википедии([2])
is_occupied
__is_continuation
____is_shifted
0 0 0: Empty Slot
0 0 1: Slot is holding start of run that has been shifted from its canonical slot.
0 1 0: not used.
0 1 1: Slot is holding continuation of run that has been shifted from its canonical slot.
1 0 0: Slot is holding start of run that is in its canonical slot.
1 0 1: Slot is holding start of run that has been shifted from its canonical slot.
Also the run for which this is the canonical slot exists but is shifted right.
1 1 0: not used.
1 1 1: Slot is holding continuation of run that has been shifted from its canonical slot.
Also the run for which this is the canonical slot exists but is shifted right.
Группа отрезков, которые идут подряд без пустых слотов между ними называется кластером(cluster). Первый слот кластера всегда не смещен(бит смещения = 0).
Пример(взят из [1])
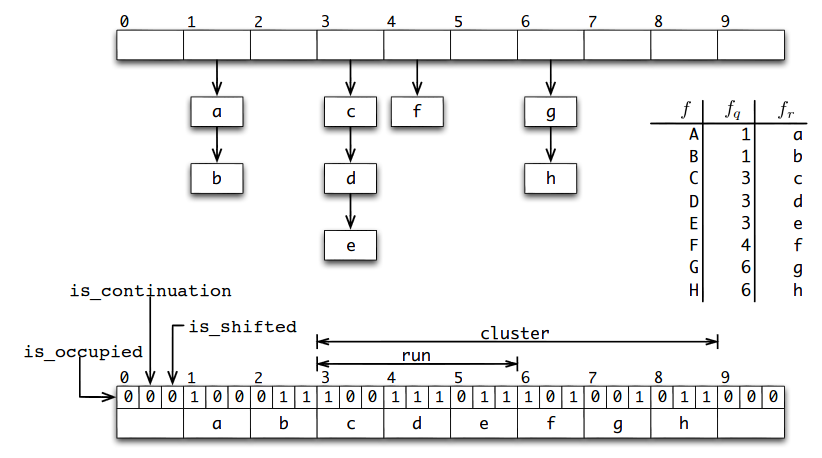
Сверху изображена хэш-таблица T. У многих элементов совпадают частные, например у a и b. Снизу изображен массив, в котором эти элементы хранятся.
Находим хэш элемента f, который потом разбиваем на частное fq и остаток fr. Проверяем слот fq в массиве. Если бит занятости не стоит — элемент не содержится в фильтре.
Если же слот занят, то необходимо найти начало отрезка. Начало отрезка может находится в положенном ему слоте, а может быть и смещено другим отрезком, поэтому ищем начало кластера.
Сначала мы идем влево от нашего слота fq, пока не найдем начало кластера(бит смещения = 0). Пока мы идем влево, запоминаем число отрезков, которое мы проскочили. Каждый слот с выставленным битом занятости — начало отрезка. С каждым таким слотом увеличиваем счетчик отрезков.
Найдя начало кластера, начинаем двигаться вправо. Каждый слот с невыставленным битом продолжения является началом нового отрезка, т. е. предыдущий отрезок закончился. С каждым таким слотом уменьшаем счетчик отрезков. Когда счетчик обнулится — мы нашли нужный нам отрезок. Бежим по нему и сравниваем с нашим остатком fr. Если отрезок закончился, а остаток не найден — элемента точно нет в фильтре. Если он был найден, то возможно элемент находится в фильтре.
Пример(взят из [2])

Ищем элемент e. Вычисляем его хэш, делим хэш на частное eq и остаток er. eq = 4. В слоте 4 стоят биты занятости и смещения (в нем находится остаток dr), следовательно элемент в этом слоте есть, но он был смещен. Ищем начало кластера.
Двигаясь влево запоминаем, что мы прошли 3 отрезка(бит занятости = 1 для слотов 4, 2, 1). Слот 1 — начало кластера(бит смещения = 0), двигаемся вправо. Начало каждого отрезка — слот с битом продолжения = 0. Для 1-ого отрезка — слот 1, для 2-ого отрезка — слот 4, для 3-его — слот 5. Проверяем каждый остаток в 3-ем отрезке, начиная со слота 5. В 3-ем отрезке всего один остаток, и он совпадает с вычисленным нами er. Ответ — элемент возможно принадлежит множеству.
По такому же алгоритму, что и поиск элемента, ищем слот для fr. Найдя слот, вставляем/удаляем fr и смещаем элементы, если необходимо. Потом выставляем (для вставки) или убираем(для удаления и если удаляемый элемент был единственным с частным = fq) бит занятости для слота A[fq].
При смещении элементов бит занятости не меняется. Если остаток был вставлен в начало отрезка, то остаток, занимавший этот слот, смещается и становится продолжением отрезка, поэтому выставляется бит продолжения. Для каждого остатка, который был смещен, ставим бит смещения.
Пример(взят из [2])
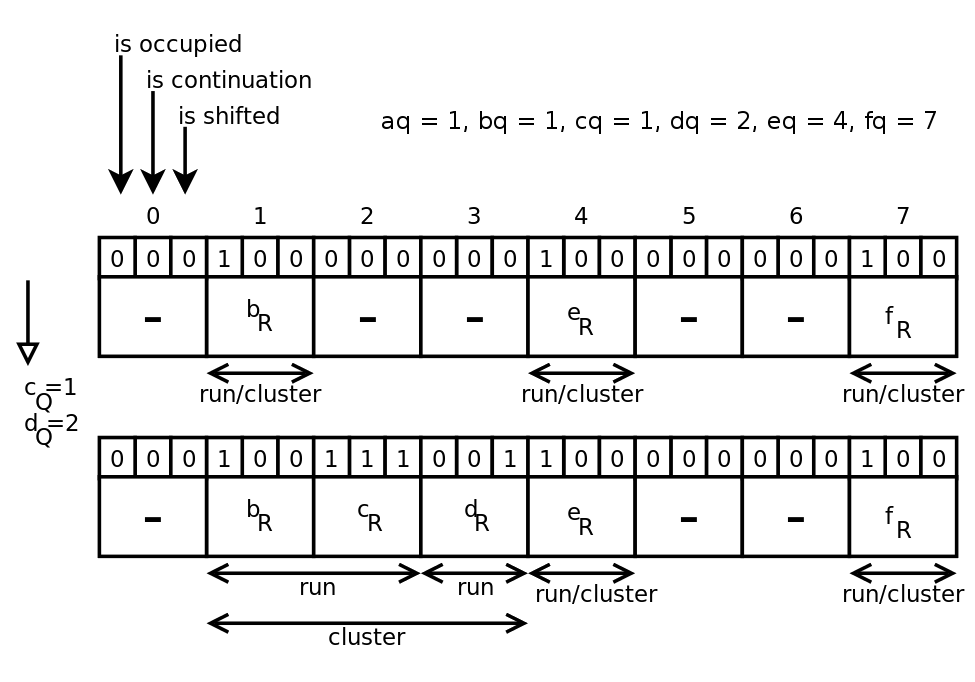
Происходит вставка элементов c и d.
bq = 1, cq = 1, br < cr, поэтому остаток cr вставляется в слот 2, проставляются биты продолжения и смещения у слота 2.
dq = 2, поэтому у слота 2 проставляется бит занятости. Но слот 2 уже занят, поэтому dr попадает в слот 3, проставляется бит смещения у слота 3.
Зачем вообще вся эта сложная система? Есть несколько преимуществ:
1. Все данные расположены последовательно в памяти. Необходимо загрузить только нужный кластер, который как правило небольшой, а не весь массив целиком. Это уменьшает количество промахов по чтению из кэша данных процессора.
2. Возможность уменьшать / увеличивать размер массива. Для этого не надо заново хэшировать данные, достаточно один бит перенести из остатка в частное или наоборот.
3. Слияние(merge) двух фильтров в один.
1. vldb.org/pvldb/vol5/p1627_michaelabender_vldb2012.pdf — описание фильтра от авторов
2. en.wikipedia.org/wiki/Quotient_filter — отличная статья на Википедии
Об ошибках и неточностях пишите — с радостью исправлю.
— элемент точно не принадлежит множеству;
— элемент возможно принадлежит множеству.
Структура
В структуре хранятся хэши элементов, которые принадлежат множеству S:
F = h(S) = {h(x) | x in S}
Именно поэтому структура вероятностная.
Допустим, мы ищем элемент A. Вычисляем его хэш и ищем в структуре.
Ситуация 1: хэш элемента не был найден. Ответ — элемент точно не принадлежит множеству.
Ситуация 2: при поиске найден хэш, но нельзя сказать точно, принадлежит ли он элементу A. Иногда бывает, что хэши двух разных элементов совпадают(это совпадение называется полной коллизией — hard collision). Поэтому нельзя сказать точно, нашли ли мы хэш элемента A или это была коллизия. Ответ — элемент возможно принадлежит множеству.
Фильтр можно представить в виде хэш-таблицы T с m = 2 ^ q группами хэшей. Для распределения хэшей по группам используется метод «quotienting»(отсюда и название фильтра). Метод был предложен Кнутом(The Art of Computer Programming:Searching and Sorting, volume 3. Section 6.4, exercise 13).
Хэш разбивается на 2 части:
частное(quotient) fq = f / (2 ^ r)
остаток(remainder) fr = f mod (2 ^ r)
В итоге добавление хэша f в фильтр сводится к добавлению части fr в группу T[fq]. Полный хэш восстанавливается по формуле:
f = fq * (2 ^ r) + fr.
Формула(взята из [2])
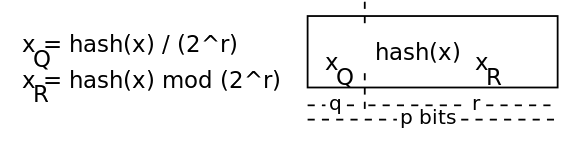
Таблица T хранится в виде массива A[0..m — 1] элементов с длиной (r + 3) бита. Каждый слот массива хранит остаток от хэша и 3 бита информации, необходимой для восстановления хэша.
Если у 2 хэшей совпадают частные, то это называется мягкой коллизией(soft collision). Все хэши, у которых совпадают частные, хранятся в массиве последовательно в отрезке(run). При этом всегда выполняется условие: если fq1 < fq2, то fr1 находится в массиве всегда перед fr2.
Информационные биты
Давайте разберемся, что делают дополнительные 3 бита, хранящиеся с каждым остатком.
1. бит занятости(is occupied). Если у слота i стоит этот бит, то в массиве есть хэш, у которого частное fq = i(но оно может быть не в этом слоте, а смещено дальше).
2. бит продолжения(is continuation). Если у слота i стоит этот бит, то хранящийся в нем остаток принадлежит тому же отрезку, что и остаток, хранящийся в предыдущем слоте i — 1.
3. бит смещения(is shifted). Если он выставлен, это значит, что хранящийся в слоте i остаток не принадлежит группе i, а просто был смещен.
Если бит смещения = 0, то в слоте i хранится остаток, принадлежащий этому слоту(fq = i). Бит продолжения позволяет понять, когда заканчивается отрезок. Бит занятости позволяет определить слот, которому принадлежит отрезок.
Хорошо описаны комбинации в Википедии([2])
is_occupied
__is_continuation
____is_shifted
0 0 0: Empty Slot
0 0 1: Slot is holding start of run that has been shifted from its canonical slot.
0 1 0: not used.
0 1 1: Slot is holding continuation of run that has been shifted from its canonical slot.
1 0 0: Slot is holding start of run that is in its canonical slot.
1 0 1: Slot is holding start of run that has been shifted from its canonical slot.
Also the run for which this is the canonical slot exists but is shifted right.
1 1 0: not used.
1 1 1: Slot is holding continuation of run that has been shifted from its canonical slot.
Also the run for which this is the canonical slot exists but is shifted right.
Группа отрезков, которые идут подряд без пустых слотов между ними называется кластером(cluster). Первый слот кластера всегда не смещен(бит смещения = 0).
Пример(взят из [1])

Сверху изображена хэш-таблица T. У многих элементов совпадают частные, например у a и b. Снизу изображен массив, в котором эти элементы хранятся.
Поиск элемента
Находим хэш элемента f, который потом разбиваем на частное fq и остаток fr. Проверяем слот fq в массиве. Если бит занятости не стоит — элемент не содержится в фильтре.
Если же слот занят, то необходимо найти начало отрезка. Начало отрезка может находится в положенном ему слоте, а может быть и смещено другим отрезком, поэтому ищем начало кластера.
Сначала мы идем влево от нашего слота fq, пока не найдем начало кластера(бит смещения = 0). Пока мы идем влево, запоминаем число отрезков, которое мы проскочили. Каждый слот с выставленным битом занятости — начало отрезка. С каждым таким слотом увеличиваем счетчик отрезков.
Найдя начало кластера, начинаем двигаться вправо. Каждый слот с невыставленным битом продолжения является началом нового отрезка, т. е. предыдущий отрезок закончился. С каждым таким слотом уменьшаем счетчик отрезков. Когда счетчик обнулится — мы нашли нужный нам отрезок. Бежим по нему и сравниваем с нашим остатком fr. Если отрезок закончился, а остаток не найден — элемента точно нет в фильтре. Если он был найден, то возможно элемент находится в фильтре.
Пример(взят из [2])

Ищем элемент e. Вычисляем его хэш, делим хэш на частное eq и остаток er. eq = 4. В слоте 4 стоят биты занятости и смещения (в нем находится остаток dr), следовательно элемент в этом слоте есть, но он был смещен. Ищем начало кластера.
Двигаясь влево запоминаем, что мы прошли 3 отрезка(бит занятости = 1 для слотов 4, 2, 1). Слот 1 — начало кластера(бит смещения = 0), двигаемся вправо. Начало каждого отрезка — слот с битом продолжения = 0. Для 1-ого отрезка — слот 1, для 2-ого отрезка — слот 4, для 3-его — слот 5. Проверяем каждый остаток в 3-ем отрезке, начиная со слота 5. В 3-ем отрезке всего один остаток, и он совпадает с вычисленным нами er. Ответ — элемент возможно принадлежит множеству.
Вставка / удаление элемента
По такому же алгоритму, что и поиск элемента, ищем слот для fr. Найдя слот, вставляем/удаляем fr и смещаем элементы, если необходимо. Потом выставляем (для вставки) или убираем(для удаления и если удаляемый элемент был единственным с частным = fq) бит занятости для слота A[fq].
При смещении элементов бит занятости не меняется. Если остаток был вставлен в начало отрезка, то остаток, занимавший этот слот, смещается и становится продолжением отрезка, поэтому выставляется бит продолжения. Для каждого остатка, который был смещен, ставим бит смещения.
Пример(взят из [2])

Происходит вставка элементов c и d.
bq = 1, cq = 1, br < cr, поэтому остаток cr вставляется в слот 2, проставляются биты продолжения и смещения у слота 2.
dq = 2, поэтому у слота 2 проставляется бит занятости. Но слот 2 уже занят, поэтому dr попадает в слот 3, проставляется бит смещения у слота 3.
Отличия от фильтра Блума
Зачем вообще вся эта сложная система? Есть несколько преимуществ:
1. Все данные расположены последовательно в памяти. Необходимо загрузить только нужный кластер, который как правило небольшой, а не весь массив целиком. Это уменьшает количество промахов по чтению из кэша данных процессора.
2. Возможность уменьшать / увеличивать размер массива. Для этого не надо заново хэшировать данные, достаточно один бит перенести из остатка в частное или наоборот.
3. Слияние(merge) двух фильтров в один.
Ссылки
1. vldb.org/pvldb/vol5/p1627_michaelabender_vldb2012.pdf — описание фильтра от авторов
2. en.wikipedia.org/wiki/Quotient_filter — отличная статья на Википедии
Об ошибках и неточностях пишите — с радостью исправлю.






