Недавно на Хабре промелькнула интересная задачка про двух мудрецов. Здесь я хочу предложить свой вариант решения и рассказать, как к этому решению можно прийти. Напомню условие:
У некоторого султана было два мудреца: Али-ибн-Вали и Вали-ибн-Али. Желая убедиться в их мудрости, султан призвал мудрецов к себе и сказал: «Я задумал два числа. Оба они целые, каждое больше единицы, но меньше ста. Я перемножил эти числа и результат сообщу Али и при этом Вали я скажу сумму этих чисел. Если вы и вправду так мудры, как о вас говорят, то сможете узнать исходные числа».
Султан сказал Али произведение, а Вали – сумму. Мудрецы задумались. Первым нарушил молчание Али.
— Я не знаю этих чисел, — сказал он, опуская голову.
— Я это знал, — подал голос Вали.
— Тогда я знаю эти числа, — обрадовался Али.
— Тогда и я знаю! — воскликнул Вали.
И мудрецы сообщили пораженному султану задуманные им числа.
Назовите эти числа.
Существует похожая задача, которая тоже была на Хабре. Она значительно проще.
Задача о Дне рождения:
Альберт и Бернард только что познакомились с Шерил. Они хотят знать, когда у неё день рождения. Шерил предложила им десять возможных дат: 15 мая, 16 мая, 19 мая, 17 июня, 18 июня, 14 июля, 16 июля, 14 августа, 15 августа и 17 августа. Затем Шерил сказала Альберту месяц своего рождения, а Бернарду — день. После этого состоялся диалог.
Альберт: Я не знаю, когда у Шерил день рождения, но я знаю, что Бернард тоже не знает.
Бернард: Поначалу я не знал, когда у Шерил день рождения, но знаю теперь.
Альберт: Теперь я тоже знаю, когда у Шерил день рождения.
Когда у Шерил день рождения?
При ближайшем рассмотрении можно увидеть, что эти две задачи совершенно идентичны.
Некоторым дням соответствуют несколько возможных месяцев, также, как некоторым произведениям соответствует несколько сумм (например, произведению 60 соответствуют суммы 15+4=19, 12+5=17 и т.д.). Некоторым месяцам соответствуют несколько дней, также, как некоторым суммам соответствуют несколько произведений (например, сумме 10 соответствуют произведения 6*4=24, 7*3=21 и т.д.). Смысл диалогов тоже совершенно одинаковый.
Это значит, что, если мы составим работающий алгоритм решения задачи о дне рождения, то сможем использовать его и для задачи о мудрецах. Разница лишь в количестве возможных комбинаций день-месяц и сумма-произведение, которые требуется перебрать. Если день рождения можно вычислить вручную на бумаге, то для поиска чисел от 1 до 100 нужно использовать программные средства. Поэтому мы сначала составим алгоритм для более простой задачи, чтобы убедиться в его правильности, а затем подставим туда исходные данные из более сложной.
Для решения я использовал MATLAB. Да, я стреляю из пушки по воробьям, но с Матлабом я часто сталкиваюсь в работе, так что пусть каждый использует инструмент, который ему привычнее.
Итак, решение.
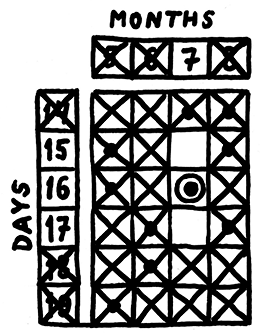
1. Запишем исходные условия: вектор с возможными значениями дней, вектор с возможными значениями месяцев и прямоугольную матрицу, в которой на местах возможных сочетаний стоят единицы.
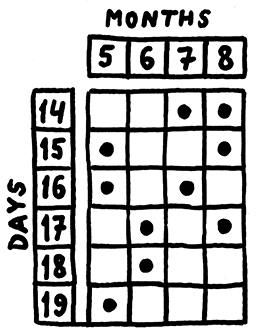
days = [14; 15; 16; 17; 18; 19];
months = [5; 6; 7; 8];
matrix = [ 0 0 1 1; 1 0 0 1; 1 0 1 0; 0 1 0 1; 0 1 0 0; 1 0 0 0 ];
2. Проанализируем первую фразу Альберта, который знает месяц:
Я не знаю, когда у Шерил день рождения, но я знаю, что Бернард тоже не знает.Из неё можно сделать вывод, что любым дням, допустимым для этого месяца, могут соответствовать больше одного месяца.
Такая ситуация невозможна для мая (ведь если день рождения 19 мая, то Бернард уже знает ответ) и для июня (если ответ – 18 июня, то Бернард тоже знает точную дату).
Чтобы исключить невозможные месяцы, нам нужно найти строки, в которых только одна единица (дни 18 и 19), найти столбцы где стоят эти единицы (месяцы 5 и 6) и вычеркнуть эти столбцы.
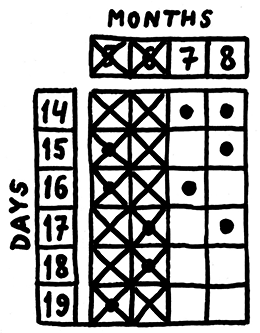
На Матлабе это действие будет выглядеть так:
unique_days = find(sum(matrix,2)==1);
[~, months_with_unique_days] = find (matrix(unique_days,:)==1);
months_with_unique_days = unique(months_with_unique_days);
matrix(:,months_with_unique_days) = [];
months(months_with_unique_days) = [];
3. После первой фразы Бернард, которому известен день, ответил:
Поначалу я не знал, когда у Шерил день рождения, но знаю теперь.
Значит, тому дню, который знает Бернард, соответствует только один месяц.
Такая ситуация возможна для чисел 15, 16 и 17.
Все строки матрицы, в которых больше одного решения или нет ни одного, нужно удалить.
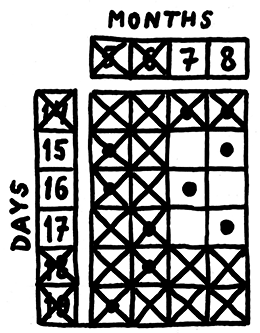
non_unique_days = find(sum(matrix,2)~=1);
matrix(non_unique_days,:) = [];
days(non_unique_days) = [];
4. Альберт, знающий месяц, ответил:
Теперь я тоже знаю, когда у Шерил день рождения.Значит, в оставшейся части матрицы остался столбец, в котором есть только один вариант. Этот столбец соответствует июлю. Выбросим все столбцы, где больше одного варианта.
non_unique_months = find(sum(matrix)~=1);
matrix(:,non_unique_months) = [];
months(non_unique_months) = [];
5. Осталось найти в оставшемся столбце единицу.
days = days(matrix == 1);
disp(days);
disp(months);
Ответ: 16 июля.
Вот полный исходный код решения.
% Birthday example
matrix = [ 0 0 1 1; 1 0 0 1; 1 0 1 0; 0 1 0 1; 0 1 0 0; 1 0 0 0 ];
days = [14; 15; 16; 17; 18; 19];
months = [5; 6; 7; 8];
% Remove months with unique days
unique_days = find(sum(matrix,2)==1);
[~, months_with_unique_days] = find (matrix(unique_days,:)==1);
months_with_unique_days = unique(months_with_unique_days);
matrix(:,months_with_unique_days) = [];
months(months_with_unique_days) = [];
% Remove non-unique days
non_unique_days = find(sum(matrix,2)~=1);
matrix(non_unique_days,:) = [];
days(non_unique_days) = [];
% Find 1 month with unique day
non_unique_months = find(sum(matrix)~=1);
matrix(:,non_unique_months) = [];
months(non_unique_months) = [];
% Find the last day
days = days(matrix == 1);
% Result output
disp(days);
disp(months);
Теперь попробуем применить этот алгоритм для задачи с мудрецами.
Месяцы заменим на все возможные суммы двух чисел от 2 до 99. Это будут целые числа от 4 до 198. Дни заменим на все возможные произведения двух чисел от 2 до 99. Таких произведений оказалось 2843. После этого сгенерируем матрицу, где будут стоять единицы на пересечениях возможных пар сумма-произведение.
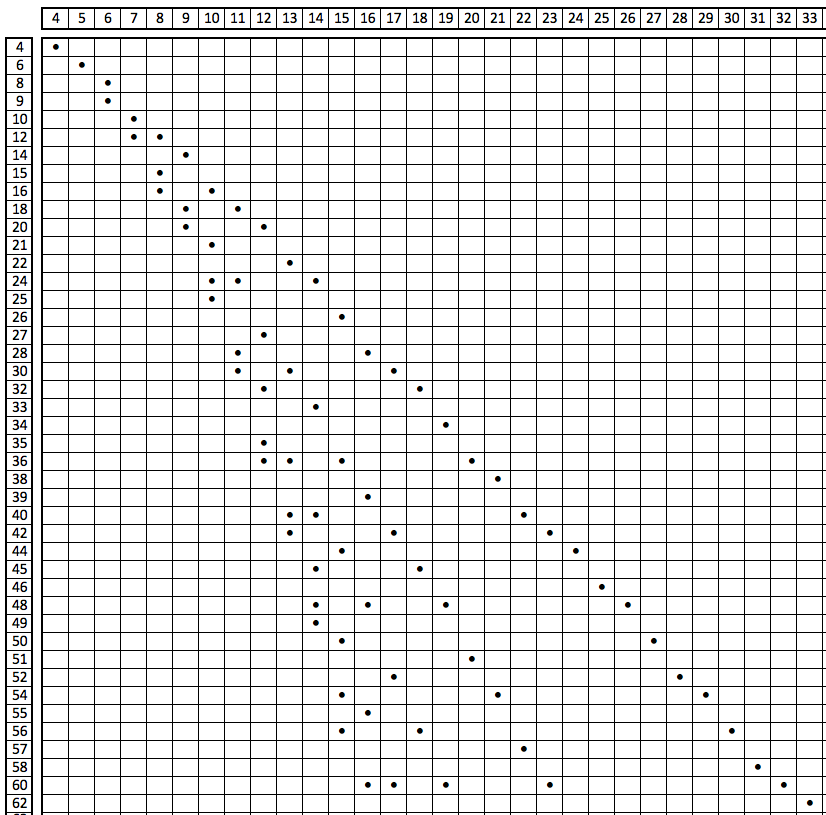
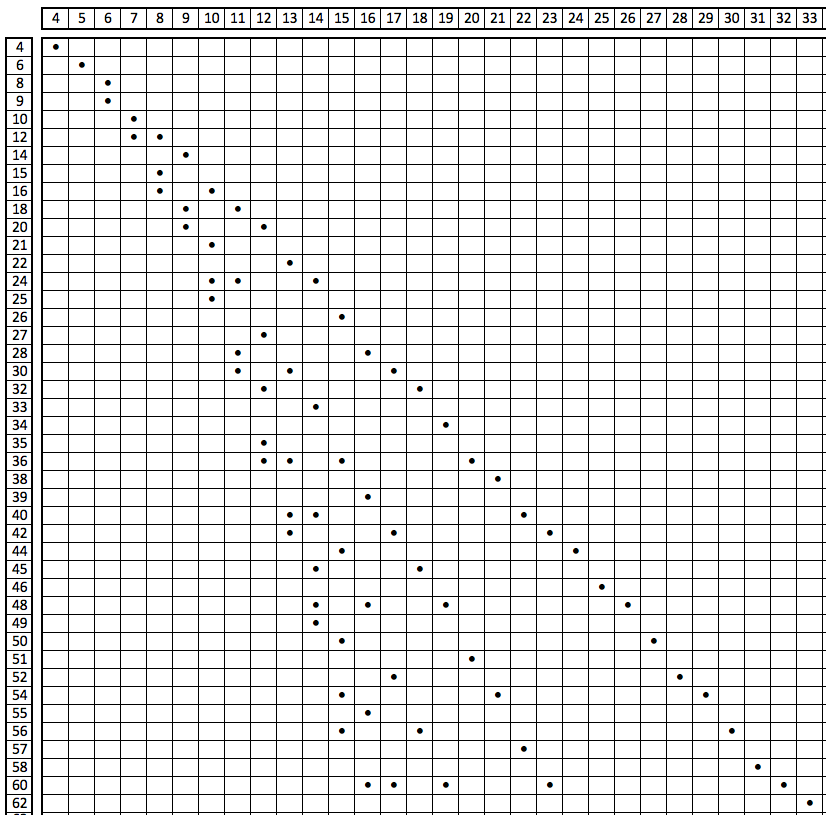
Небольшой фрагмент этой таблицы (примерно 1/400)
По горизонтальной оси – суммы, по вертикальной – произведения.
months = 4:198;
days = unique((2:99)'*(2:99));
matrix = false(length(days),length(months));
for i1 = 2:99
for i2 = 2:99
matrix(days==(i1*i2),months==(i1+i2)) = true;
end;
end;
Запустим программу и получим ответ: произведение – 52, сумма – 17.
Это соответствует паре чисел 4 и 13.






