В результате размышлений над особенностями стандарта IEEE754, я пришел к выводу, что многие положения, на которых основывается данный стандарт, зиждутся на ошибочном методологическом подходе. А именно, авторы стандарта за основу рассуждений взяли заданный формат машинного слова. Затем, исходя из заданного формата, были сформулированы требования к множеству чисел, которые могут быть представимы в этом формате. Было высказано ряд бездоказательных суждений. Например, о предпочтении использования в компьютерной арифметике дробной мантиссы. Или об обязательной потере точности, при представлении чисел в ненормализованном виде, а также недопустимости неоднозначного представления действительных чисел в экспоненциальном виде.
Отсюда родились требования к обязательной нормализации чисел после каждого арифметического действия, и как следствие, большие проблемы с представлением чисел, лежащих вблизи нуля, а также невозможность получения нуля в явном виде. Это все приводит к неоправданным затратам вычислительных ресурсов на нормализацию и борьбу с ее последствиями.
Предлагаемая здесь работа является логическим продолжением предыдущих двух моих топиков на Хабре. В своих рассуждениях я оттолкнулся от естественного представления чисел и ограничений, которые накладываются на числа, вследствие конечности носителя, на который они записываются. Такой подход позволил получить ряд очень важных выводов. Основной из них заключается в том, что процесс нормализации не является обязательным на всех этапах проведения арифметических операций. Более того, именно обязательная нормализация привела к необходимости введения специального класса денормализованных чисел, что существенно увеличило программно-аппаратные затраты.
Предложенный подход позволил прийти к выводу, что, добавлением всего одного разряда в машинном слове, можно в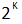 раз расширить диапазон представимых чисел в формате с плавающей точкой, где К — количество разрядов машинной мантиссы.
раз расширить диапазон представимых чисел в формате с плавающей точкой, где К — количество разрядов машинной мантиссы.
В статье вы найдете целый ряд нетривиальных выводов, которые позволяют по-новому взглянуть на представление чисел с плавающей запятой в машинном коде.















Отсюда родились требования к обязательной нормализации чисел после каждого арифметического действия, и как следствие, большие проблемы с представлением чисел, лежащих вблизи нуля, а также невозможность получения нуля в явном виде. Это все приводит к неоправданным затратам вычислительных ресурсов на нормализацию и борьбу с ее последствиями.
Предлагаемая здесь работа является логическим продолжением предыдущих двух моих топиков на Хабре. В своих рассуждениях я оттолкнулся от естественного представления чисел и ограничений, которые накладываются на числа, вследствие конечности носителя, на который они записываются. Такой подход позволил получить ряд очень важных выводов. Основной из них заключается в том, что процесс нормализации не является обязательным на всех этапах проведения арифметических операций. Более того, именно обязательная нормализация привела к необходимости введения специального класса денормализованных чисел, что существенно увеличило программно-аппаратные затраты.
Предложенный подход позволил прийти к выводу, что, добавлением всего одного разряда в машинном слове, можно в
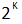 раз расширить диапазон представимых чисел в формате с плавающей точкой, где К — количество разрядов машинной мантиссы.
раз расширить диапазон представимых чисел в формате с плавающей точкой, где К — количество разрядов машинной мантиссы.В статье вы найдете целый ряд нетривиальных выводов, которые позволяют по-новому взглянуть на представление чисел с плавающей запятой в машинном коде.