Привет Хабр! Данная публикация возникла после просматривания этого поста, в котором автор пытается посчитать количество различных судоку. Желая более точно разобраться в вопросе, я за пару минут нагуглил точный ответ, приведенный в данной статье. Текст этой статьи мне показался интересным сам по себе, поэтому я решил сделать перевод (в довольно вольном стиле).

К сожалению, оригинал данной статьи написан длядебилов очень широкого круга читателей, в том плане, что тема рассматривается не очень глубоко, но довольно подробно. При этом поясняется только общий подход к решению задачи, без технических деталей, и, фактически, обрывается на самом интересном месте формулировкой «ну а дальше они посчитали на компьютере». В итоге я немного дополнил изложение своими комментариями: они либо отмечены курсивом, либо спрятаны под спойлеры. В них раскрываются некоторые технические моменты более подробно. Возможно, пост вместе с этими комментариями суммарно тянет на полноценную статью, нежели чем на просто перевод, но я решил оставить все как есть (на самом деле, я не нашел кнопки перевода перевода обратно в обычную статью, а создавать новую публикацию только ради этого было лень).
Судоку — это головоломка, которая завоевала мировую популярность с 2005 года. Для того, чтобы решить судоку, нужны только логика и метод проб и ошибок. Сложная математика появляются лишь при более пристальном рассмотрении: для подсчета количества различных сеток судоку нужна комбинаторика, чтобы определить количество этих сеток без учета всевозможных симметрий понадобится теория групп, а для решения судоку в промышленных масштабах — теория сложности алгоритмов.
Впервые головоломка судоку в известном нам виде была опубликована в 1979 году в американском журнале Dell Magazines под названием «Numbers in Place» за авторством Говарда Гэрнса (Howard Garns). В 1984 году судоку впервые было опубликовано в Японии в журнале Nikoli. Именно Маки Кадзи (Maki Kaji), президент компании Nikoli (которая, кстати, специализируется на всяких пазлах и логических играх), дал головоломке название «судоку», что в переводе с японского означает «одинокие числа». Когда игра стала популярной в Японии, на нее обратил внимание новозеландец Вэйн Гулд (Wayne Gould). Вэйн написал программу, которая могла генерировать сотни судоку. В 2004 году он опубликовал некоторые из этих пазлов в Лондонских газетах. Вскоре после этого лихорадка судоку охватила всю Англию. В 2005 году головоломка стала популярной в Соединенных Штатах. Судоку стали регулярно публиковаться во множестве газет и журналов, радуя людей по всему миру.
Классическая версия судоку имеет вид квадратной таблицы 9×9, итого — 81 ячейка. Эта таблица разделена на 9 блоков 3×3. В некоторых ячейках находятся числа из множества {1,2,3,4,5,6,7,8,9} (эти числа нельзя менять), остальные ячейки пусты. Цель игры — заполнить все пустые ячейки, используя только вышеупомянутые девять чисел, так, чтобы на каждой горизонтали, на каждой вертикали, а также в каждом блоке каждое из чисел присутствовало бы ровно один раз. Мы будем называть эти ограничения Главным Правилом игры.
Описанные выше правила относятся к судоку порядка 3. В общем же случае, судоку порядка n — это таблица n2×n2, разделенная на n2 блоков размера n×n каждый. И все это нужно заполнить числами от 1 до n2 так, чтобы выполнялось Главное Правило.
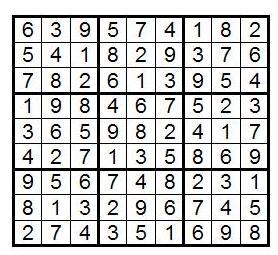
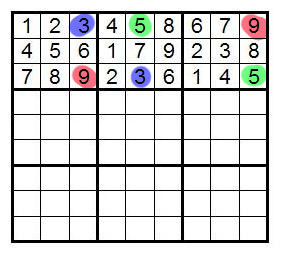
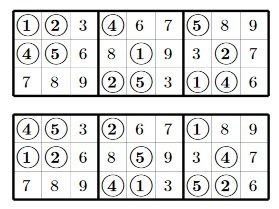
Например, на следующей картинке можно видеть пример судоку, а также его решение:
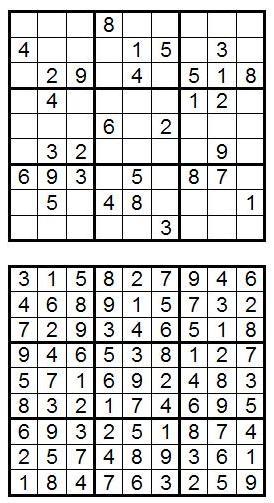
Говорят, для решения судоку не нужна математика — это не правда. Это на самом деле означает, что не нужна только арифметика. Головоломка не зависит от того факта, что мы используем цифры от 1 до 9. Мы можем с легкостью заменить эти 9 цифр на буквы, цвета или сорта суши. Фактически, для решения судоку нужно применять такой вид математического мышления, как логическая дедукция.
Самая простая эвристика для решения судоку — сначала для каждой пустой клетки выписать всевозможные числа, которые туда можно записать, не противореча Главному Правилу, ориентируясь по числам, данным изначально. Если для какой-то ячейки возможен только один вариант — именно его нужно записать в эту ячейку.
Другой подход для решения — выбрать число, а после этого — строку, столбец или блок. После этого следует рассмотреть все позиции в строке/столбце/блоке и проверить, можно ли туда поместить выбранное число, не нарушая Главного Правила. Если число подходит только для одной позиции — можно смело его туда вписать. Как только это будет сделано, выбранное число может быть исключено из возможных вариантов для всех остальных пустых ячеек в соответствующих строке, столбце и блоке.
Обычно этих двух правил не достаточно для полного заполнения сетки судоку. Часто требуется более сложные методы для достижения прогресса, а иногда требуется перебирать варианты и откатываться в случае неудачного выбора. Более изощренная стратегия состоит в том, чтобы рассмотреть пары или тройки ячеек в строке, столбце или блоке. Может оказаться, что для рассматриваемой пары ячеек подходят только два числа из группы, но непонятно какое из них в какую из этих двух ячеек поместить. Однако, из этого можно заключить, что числа из данной пары не могут появиться на каких либо других местах в рассматриваемой группе. Это уменьшает количество вариантов в других пустых ячейках и помогает подобраться ближе к решению. Аналогично, если тройку чисел можно поместить только в определенную тройку позиций (непонятно в каком порядке), то эти три числа можно исключить из рассмотрения для всех остальных ячеек по соседству.
Заметим, что кроме данных эвристик существует множество других. Вы даже можете придумать свои собственные стратегии решения.
Когда ни одна из простых эвристик не помогает — нужно попробовать выбрать пустую ячейку с наименьшим числом вариантов и попробовать один из вариантов. В случае получения противоречия (повторяющиеся числа в строке, столбце или блоке) следует отменить все свои действия до момента выбора и попробовать другой вариант.
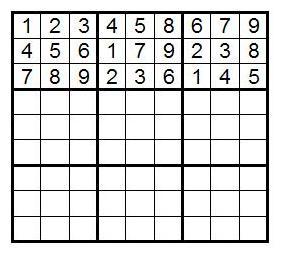
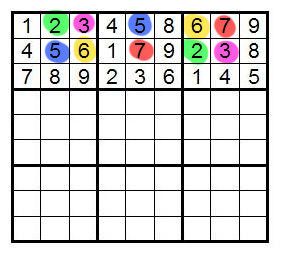
Упражнение: Попробуйте применить описанные выше методы на этом судоку:
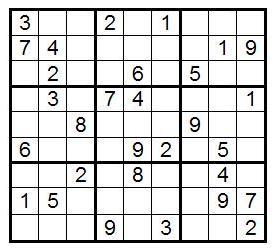
В интернете можно найти множество других судоку любой сложности и на любой вкус.
Это очень интересный вопрос. Так сколько же различных судоку 9×9? Сколькими способами можно заполнить таблицу 9×9 числами от 1 до 9 так, чтобы выполнялось Главное Правило? Мы опишем метод, с помощью которого Бертрам Фельгенхауэр (Bertram Felgenhauer) и Фразер Джарвис (Frazer Jarvis) посчитали это количество в начале 2006 года.
Сначала договоримся об обозначениях. Будем называть полосой тройку блоков, центры которых расположены на одной горизонтали. Итого мы имеем три полосы — верхнюю, нижнюю и среднюю. Стеком будем называть тройку блоков, центры которых расположены на одной вертикали. Стеков, как и полос, у нас тоже три — левый, правый и средний. Ячейку на пересечении i-й строки и j-го столбца будем обозначать как (i,j).
Приготовления окончены и мы готовы посчитать число N — количество различных судоку. Сперва обозначим все блоки судоку следующим образом:
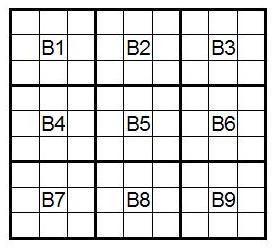
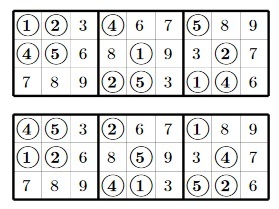
Сколькими способами можно заполнить блок B1? Поскольку для блока B1 у нас 9 чисел, одно для кажой ячейки, в первую из них мы можем записать одно из чисел одним из 9 способов. Для каждого из этих 9 способов у нас есть 8 способов разместить одно из оставшихся чисел ровно 8 способами. Для третьей ячейки для каждого из этих 9×8 способов количество вариантов идти дальше — ровно 7. Мы, по сути, пытаемся построить всевозможные перестановки длины 9 и нужное нам количество способов заполнить блок B1 равно количеству этих перестановок — 9! = 9×8×7×6×7×4×3×2×1 = 362880. Начиная с судоку, в котором блок B1 заполнен определенным образом, мы можем получить судоку с любым другим заполнением блока B1 с помощью простого переобозначния чисел (вспомним, что нам неважно какие числа где находятся — главное знать где одинаковые числа, а где различные). Поэтому, для простоты, заполним блок B1 числами от 1 до 9 в порядке, показанном на рисунке:
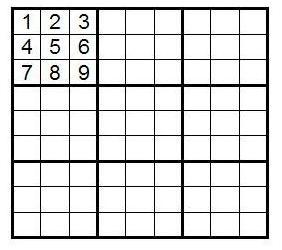
Пусть количество судоку, в которых блок B1 заполнен именно так, как на картинке, равно N1. Общее количество судоку будет N1×9!, отсюда N1=N/9!.
Рассмотрим все способы заполнить первую строку в блоках B2 и B3. Поскольку 1, 2 и 3 уже присутствуют в блоке B1, эти числа больше не могут быть использованы в данной строке. Только числа 4, 5, 6, 7, 8 и 9 из второй и третьей строк блока B1 могут быть использованы в первой строке блоков B2 и B3.
Упражнение: Перечислите все возможные способы заполнения первой строки в блоках B2 и B3 с точностью до перестановки цифр. Подсказка: всего имеется десять способов разбиения шести чисел на две части по три, а меняя B2 на B3, мы получаем еще десять способов. Итого — двадцать.
Назовем два из этих вариантов чистыми верхними строками: когда числа {4,5,6}, как во второй строке блока B1 располагаются вместе в B2, а числа {7,8,9}, как в третьей строке блока B1, располагаются вместе в B3 (ну и случай, когда B2 и B3 поменяны местами). Все остальные способы — это смешанные верхние строки, поскольку там в первой строке B2 и B3 множества {4,5,6} и {7,8,9} смешаны друг с другом.
Ну так вот, у нас есть эти двадцать способов, и мы хотим узнать, как заполнить остальные ячейки в первой полосе.
Упражнение: Подумайте немного о том, как можно заполнить первую полосу начиная с чистой верхней строки 1,2,3;{4,5,6};{7,8,9} (мы пишем a,b,c, если три числа идут в зафиксированном порядке и {a,b,c}, если эти числа могут идти в любом порядке). Сколько всего есть способов, считая различные способы порядка в B2 и B3? Верно, что этих способов столько же, сколько и для другой чистой строки 1,2,3;{7,8,9};{4,5,6}?
Помните, мы не меняем порядок в блоке B1, поскольку мы уже учитываем колчество сеток, которые получаются путем перемешивания девяки чисел в B1.
Оказывается, для чистой верхней строки 1,2,3;{4,5,6};{7,8,9} — ровно (3!)6 способов, поскольку нам обязательно нужно поместить {7,8,9};{1,2,3} на вторую строку в блоках B2 и B3, а {1,2,3};{4,5,6} — на третью строку. После этого мы можем произвольным образом менять местами числа в этих шести тройках в B2 и B3 для того, чтобы получить все конфигурации. Для второй чистой верхней строки ответ тот же, поскольку все, что мы меняется местами — это блоки B2 и B3.
Для случая смешанных верхних строк все неммого сложнее. Давайте рассмотрим верхнюю строку 1,2,3;{4,6,8};{5,7,9}. Далее первую полосу можно заполнить так, как показано на картинке ниже, где a, b и c — это числа 1, 2, 3 в любом порядке.
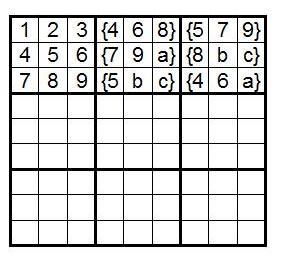
Как только число a выбрано, b и c — это оставшиеся два числа в любом порядке, поскольку они находятся в одних и тех же строках. Для a три способа выбора, а затем мы можем просто перемешать числа в шести тройках в B2 и B3 в любом порядке — и всегда будет получаться подходящая первая полоса. Итого, количество конфигураций — 3x(3!)6. Несложно показать, что в оставшихся семнадцати способах мы получим то же самое число.
Теперь мы можем посчитать общее количество различных верхних полос для фиксированного блока B1: 2х(3!)6+18x3x(3!)6=2612736. Первая часть суммы — это количество полос для чистых верхних полос, а вторая — для смешанных.
Вместо того, чтобы посчитать количество разничных полностью заполненных сеток для каждого из этих 2612736 вариантов, Фельгенхауэр и Джарвис сначала определили у каких из этих верхних полос одно и то же количество вариантов полного заполнения. Этот анализ сокращает количество полос, которые нам нужно будет рассмотреть для дальнейших рассчетов.
Есть несколько операций, которые оставляют количество полностью заполненных сеток неизменным: переназначение чисел, перестановка любых блоков в первой полосе, перемешивание столбцов в любом блоке, изменение порядка трех строк в полосе. Как только какие либо из операций меняют порядок чисел в B1 — мы просто переназначаем числа так, чтобы привести блок B1 к стандартному виду.
Когда мы меняем местами блоки B1, B2 и B3 — количество заполнений сеток сохраняется, поскольку мы начинаем с корректной сетки судоку, и единственный способ сохранить корректность в дальнейшем — это поменяить местами B4, B5, B6 и B7, B8, B9 так, как мы поменяли B1, B2, B3. В итоге все стеки останутся теми же самыми. Другими словами, каждое корректное заполнение всей сетки для одной верхней полосы дает ровно одно корректное заполнение сетки для другой верхней полосы, полученной перемешиванием блоков B1, B2, B3.
Упражнение: Убедитесь сами, что если поменять местами блоки B2 и B3 в следующей сетке, то единственный способ сохранить сетку корректной — это поменять местами B5 и B6, а также B8 и B9. Стеки остаются те же самые, но меняются их расположения.
Упражнение: Пусть у вас есть корректно заполненная сетка судоку и вы меняете местами некоторые столбцы в каком либо из блоков B1, B2 или B3. Что нужно дополнительно сделать с остальными столбцами, чтобы сетка судоку осталась корректной? Например, если вы поменяли местами первый и второй столбцы в блоке B2, как бы вы исправили оставшуюся часть сетки так, чтобы она все еще удовлетворяла Главному Правилу?
Последнее упражнение говорит нам о том, что каждое заполнение первой полосы дает нам уникальное заполнение для такой первой полосы, в которой столбцы упорядочены определенным образом внутри блоков.
Это наблюдение позволяет нам уменьшить количество первых полос, которые нам нужно рассмотреть. Согласно Фельгенхауэру и Джарвису, мы перемешиваем столбцы в блоках B2 и B3 таким образом, что значения в самой верхней строке идут в возрастающем порядке. После этого мы возможно меняем местами блоки B2 и B3 так, чтобы самое первое число в блоке B2 (левое верхнее) было меньше, чем самое первое число в блоке B3. Эта операция называется лексикографической редукцией. Поскольку для каждого из двух блоков у нас ровно 6 различных перестановок и всего 2 способа упорядочить блоки друг относительно друга, лексикографическая редукция говорит нам, что для любой первой полосы можно построить класс из 62×2=72 первых полос с одним и тем же количеством полных заполнений сеток (и для всех элементов из каждого класса это построение будет приводить к этому же классу). Таким образом, нам теперь нужно рассмотреть только 2612736/72=36288 первых полос.
Для каждого из этих вариантов рассмотрим всевозможные перестановки трех верхних блоков: их ровно 6. А для каждого из этих вариантов имеется 63 перестановок столбцов внутри всех блоков. После того, как мы все перемешали, вы переназначаем числа так, чтобы в блоке B1 они все шли в стандартном порядке. Мы также можем произвольно перемешать три верхние строки, после чего опять переназначить числа, чтобы блок B1 стал стандартным. После каждой из этих операций количество заполнение всей сетки для данной первой полосы останется неизменным. Фельгенхауэр и Джарвис при помощи компьютерной программы определили, что эти операции сокращают количество первых полос, которые имеет смысл рассматривать, с 36288 до всего лишь 416.
Упражнение: Рассмотрите определенную первую полосу. Проделайте над ней некоторые операции, которые сохраняют количество заполнений всей сетки судоку. Можете начать со следующего: поменяйте местами первую и вторую строки. После этого переназначьте числа в блоке B1, чтобы привести его к стандартной форме. Выполните лексикографическую редукцию.
Главное, на что следует обратить внимание: полоса, с которой мы начали, и полоса, которой закончили, имеют одинаковое количество заполнения всей сетки судоку. Поэтому вместо вычисления количества заполнений сеток для каждой полосы мы можем подсчитывать их количество только для одной из них.
Существует еще несколько операций, которые сокращают количество сеток для рассмотрения. Если у нас есть пара чисел {a,b} такая, что a и b находятся в одном столбце, причем a — на i-й строке, а b — на j-ой, и, ко всему прочему, есть такая же пара в другом столбце, причем для этого столбца a уже находится на j-ой строке, а b — на i-ой (т.е. эти четыре числа находятся в углах некоторого прямоугольника, и противоположные числа равны), то мы можем поменять местами числа в обеих парах и получить новую корректную полосу с тем же количеством конечных сеток. Например, в судоку, приведенном чуть выше, числа 8 и 9 в шестом и девятом столбцах формируют такую конфигурацию. Рассмотрев все возможные случаи, Фельгенхауэр и Джарвис сократили необходимое для рассмотрения число первых полос с 416 до 174.
Но и это еще не все. Они рассмотрели другие конфигурации одинаковых множеств (из трех и более чисел), лежащих друг напротив друга в двух различных столбцах или строках, которые можно поменять местами и ответ от этого не изменится. Это сокращает количество вариантов до 71, а если дополнительно рассмотреть эти варианты и применить там более сложные симметрии — количество полос для рассмотрения можно сократить до 44. И для каждой из этих 44 полос все остальные полосы в соответствующем классе имеют такое же количество полных заполнений всей сетки.
Пусть C — одна из 44 полос. Тогда количество способов, которым C можно дополнить до полной сетки судоку, обозначим на nC. Нам также понадобится число mC — общее количество полос, для которых количество конечных заполнений такое же, как и у C. Когда общее количество различных судоку будет равно N=ΣCmCnC, то есть сумма mCnC по всем 44 полосам.
Фельгенхауэр и Джарвис написали компьютерную программу для выполнения итоговых рассчетов. Они вычислили число N1 (количество корректных заполнений, в которых B1 в стандартной форме) для каждой из 44 полос. Затем они умножили это число за 9!, чтобы получить ответ. Они обнаружили, что количество всевозможных корректных сеток судоку 9 на 9 равно N=6670903752021072936960, что приблизительно равно 6.671×1021.
В следующей части мы посчитаем количество действительно различных судоку, считая что два судоку одинаковые, если они переходят друг в друга поворотами, отражениями, перемешиванием столбцов и так далее. Для этого мы погрузимся в теорию групп, познакомимся с леммой Бернсайда и, конечно же, напишем аццкую программу для подсчета ответа. В общем, не пропустите.

К сожалению, оригинал данной статьи написан для
Введение
Судоку — это головоломка, которая завоевала мировую популярность с 2005 года. Для того, чтобы решить судоку, нужны только логика и метод проб и ошибок. Сложная математика появляются лишь при более пристальном рассмотрении: для подсчета количества различных сеток судоку нужна комбинаторика, чтобы определить количество этих сеток без учета всевозможных симметрий понадобится теория групп, а для решения судоку в промышленных масштабах — теория сложности алгоритмов.
Впервые головоломка судоку в известном нам виде была опубликована в 1979 году в американском журнале Dell Magazines под названием «Numbers in Place» за авторством Говарда Гэрнса (Howard Garns). В 1984 году судоку впервые было опубликовано в Японии в журнале Nikoli. Именно Маки Кадзи (Maki Kaji), президент компании Nikoli (которая, кстати, специализируется на всяких пазлах и логических играх), дал головоломке название «судоку», что в переводе с японского означает «одинокие числа». Когда игра стала популярной в Японии, на нее обратил внимание новозеландец Вэйн Гулд (Wayne Gould). Вэйн написал программу, которая могла генерировать сотни судоку. В 2004 году он опубликовал некоторые из этих пазлов в Лондонских газетах. Вскоре после этого лихорадка судоку охватила всю Англию. В 2005 году головоломка стала популярной в Соединенных Штатах. Судоку стали регулярно публиковаться во множестве газет и журналов, радуя людей по всему миру.
Классическая версия судоку имеет вид квадратной таблицы 9×9, итого — 81 ячейка. Эта таблица разделена на 9 блоков 3×3. В некоторых ячейках находятся числа из множества {1,2,3,4,5,6,7,8,9} (эти числа нельзя менять), остальные ячейки пусты. Цель игры — заполнить все пустые ячейки, используя только вышеупомянутые девять чисел, так, чтобы на каждой горизонтали, на каждой вертикали, а также в каждом блоке каждое из чисел присутствовало бы ровно один раз. Мы будем называть эти ограничения Главным Правилом игры.
Описанные выше правила относятся к судоку порядка 3. В общем же случае, судоку порядка n — это таблица n2×n2, разделенная на n2 блоков размера n×n каждый. И все это нужно заполнить числами от 1 до n2 так, чтобы выполнялось Главное Правило.
Например, на следующей картинке можно видеть пример судоку, а также его решение:
Подходы к решению
Говорят, для решения судоку не нужна математика — это не правда. Это на самом деле означает, что не нужна только арифметика. Головоломка не зависит от того факта, что мы используем цифры от 1 до 9. Мы можем с легкостью заменить эти 9 цифр на буквы, цвета или сорта суши. Фактически, для решения судоку нужно применять такой вид математического мышления, как логическая дедукция.
Самая простая эвристика для решения судоку — сначала для каждой пустой клетки выписать всевозможные числа, которые туда можно записать, не противореча Главному Правилу, ориентируясь по числам, данным изначально. Если для какой-то ячейки возможен только один вариант — именно его нужно записать в эту ячейку.
Другой подход для решения — выбрать число, а после этого — строку, столбец или блок. После этого следует рассмотреть все позиции в строке/столбце/блоке и проверить, можно ли туда поместить выбранное число, не нарушая Главного Правила. Если число подходит только для одной позиции — можно смело его туда вписать. Как только это будет сделано, выбранное число может быть исключено из возможных вариантов для всех остальных пустых ячеек в соответствующих строке, столбце и блоке.
Обычно этих двух правил не достаточно для полного заполнения сетки судоку. Часто требуется более сложные методы для достижения прогресса, а иногда требуется перебирать варианты и откатываться в случае неудачного выбора. Более изощренная стратегия состоит в том, чтобы рассмотреть пары или тройки ячеек в строке, столбце или блоке. Может оказаться, что для рассматриваемой пары ячеек подходят только два числа из группы, но непонятно какое из них в какую из этих двух ячеек поместить. Однако, из этого можно заключить, что числа из данной пары не могут появиться на каких либо других местах в рассматриваемой группе. Это уменьшает количество вариантов в других пустых ячейках и помогает подобраться ближе к решению. Аналогично, если тройку чисел можно поместить только в определенную тройку позиций (непонятно в каком порядке), то эти три числа можно исключить из рассмотрения для всех остальных ячеек по соседству.
Заметим, что кроме данных эвристик существует множество других. Вы даже можете придумать свои собственные стратегии решения.
Когда ни одна из простых эвристик не помогает — нужно попробовать выбрать пустую ячейку с наименьшим числом вариантов и попробовать один из вариантов. В случае получения противоречия (повторяющиеся числа в строке, столбце или блоке) следует отменить все свои действия до момента выбора и попробовать другой вариант.
Упражнение: Попробуйте применить описанные выше методы на этом судоку:
В интернете можно найти множество других судоку любой сложности и на любой вкус.
Так сколько же их?
Это очень интересный вопрос. Так сколько же различных судоку 9×9? Сколькими способами можно заполнить таблицу 9×9 числами от 1 до 9 так, чтобы выполнялось Главное Правило? Мы опишем метод, с помощью которого Бертрам Фельгенхауэр (Bertram Felgenhauer) и Фразер Джарвис (Frazer Jarvis) посчитали это количество в начале 2006 года.
Сначала договоримся об обозначениях. Будем называть полосой тройку блоков, центры которых расположены на одной горизонтали. Итого мы имеем три полосы — верхнюю, нижнюю и среднюю. Стеком будем называть тройку блоков, центры которых расположены на одной вертикали. Стеков, как и полос, у нас тоже три — левый, правый и средний. Ячейку на пересечении i-й строки и j-го столбца будем обозначать как (i,j).
Приготовления окончены и мы готовы посчитать число N — количество различных судоку. Сперва обозначим все блоки судоку следующим образом:
Сколькими способами можно заполнить блок B1? Поскольку для блока B1 у нас 9 чисел, одно для кажой ячейки, в первую из них мы можем записать одно из чисел одним из 9 способов. Для каждого из этих 9 способов у нас есть 8 способов разместить одно из оставшихся чисел ровно 8 способами. Для третьей ячейки для каждого из этих 9×8 способов количество вариантов идти дальше — ровно 7. Мы, по сути, пытаемся построить всевозможные перестановки длины 9 и нужное нам количество способов заполнить блок B1 равно количеству этих перестановок — 9! = 9×8×7×6×7×4×3×2×1 = 362880. Начиная с судоку, в котором блок B1 заполнен определенным образом, мы можем получить судоку с любым другим заполнением блока B1 с помощью простого переобозначния чисел (вспомним, что нам неважно какие числа где находятся — главное знать где одинаковые числа, а где различные). Поэтому, для простоты, заполним блок B1 числами от 1 до 9 в порядке, показанном на рисунке:
Пусть количество судоку, в которых блок B1 заполнен именно так, как на картинке, равно N1. Общее количество судоку будет N1×9!, отсюда N1=N/9!.
Рассмотрим все способы заполнить первую строку в блоках B2 и B3. Поскольку 1, 2 и 3 уже присутствуют в блоке B1, эти числа больше не могут быть использованы в данной строке. Только числа 4, 5, 6, 7, 8 и 9 из второй и третьей строк блока B1 могут быть использованы в первой строке блоков B2 и B3.
Упражнение: Перечислите все возможные способы заполнения первой строки в блоках B2 и B3 с точностью до перестановки цифр. Подсказка: всего имеется десять способов разбиения шести чисел на две части по три, а меняя B2 на B3, мы получаем еще десять способов. Итого — двадцать.
Назовем два из этих вариантов чистыми верхними строками: когда числа {4,5,6}, как во второй строке блока B1 располагаются вместе в B2, а числа {7,8,9}, как в третьей строке блока B1, располагаются вместе в B3 (ну и случай, когда B2 и B3 поменяны местами). Все остальные способы — это смешанные верхние строки, поскольку там в первой строке B2 и B3 множества {4,5,6} и {7,8,9} смешаны друг с другом.
Ну так вот, у нас есть эти двадцать способов, и мы хотим узнать, как заполнить остальные ячейки в первой полосе.
Упражнение: Подумайте немного о том, как можно заполнить первую полосу начиная с чистой верхней строки 1,2,3;{4,5,6};{7,8,9} (мы пишем a,b,c, если три числа идут в зафиксированном порядке и {a,b,c}, если эти числа могут идти в любом порядке). Сколько всего есть способов, считая различные способы порядка в B2 и B3? Верно, что этих способов столько же, сколько и для другой чистой строки 1,2,3;{7,8,9};{4,5,6}?
Помните, мы не меняем порядок в блоке B1, поскольку мы уже учитываем колчество сеток, которые получаются путем перемешивания девяки чисел в B1.
Оказывается, для чистой верхней строки 1,2,3;{4,5,6};{7,8,9} — ровно (3!)6 способов, поскольку нам обязательно нужно поместить {7,8,9};{1,2,3} на вторую строку в блоках B2 и B3, а {1,2,3};{4,5,6} — на третью строку. После этого мы можем произвольным образом менять местами числа в этих шести тройках в B2 и B3 для того, чтобы получить все конфигурации. Для второй чистой верхней строки ответ тот же, поскольку все, что мы меняется местами — это блоки B2 и B3.
Для случая смешанных верхних строк все неммого сложнее. Давайте рассмотрим верхнюю строку 1,2,3;{4,6,8};{5,7,9}. Далее первую полосу можно заполнить так, как показано на картинке ниже, где a, b и c — это числа 1, 2, 3 в любом порядке.
Как только число a выбрано, b и c — это оставшиеся два числа в любом порядке, поскольку они находятся в одних и тех же строках. Для a три способа выбора, а затем мы можем просто перемешать числа в шести тройках в B2 и B3 в любом порядке — и всегда будет получаться подходящая первая полоса. Итого, количество конфигураций — 3x(3!)6. Несложно показать, что в оставшихся семнадцати способах мы получим то же самое число.
Теперь мы можем посчитать общее количество различных верхних полос для фиксированного блока B1: 2х(3!)6+18x3x(3!)6=2612736. Первая часть суммы — это количество полос для чистых верхних полос, а вторая — для смешанных.
Вместо того, чтобы посчитать количество разничных полностью заполненных сеток для каждого из этих 2612736 вариантов, Фельгенхауэр и Джарвис сначала определили у каких из этих верхних полос одно и то же количество вариантов полного заполнения. Этот анализ сокращает количество полос, которые нам нужно будет рассмотреть для дальнейших рассчетов.
Есть несколько операций, которые оставляют количество полностью заполненных сеток неизменным: переназначение чисел, перестановка любых блоков в первой полосе, перемешивание столбцов в любом блоке, изменение порядка трех строк в полосе. Как только какие либо из операций меняют порядок чисел в B1 — мы просто переназначаем числа так, чтобы привести блок B1 к стандартному виду.
Когда мы меняем местами блоки B1, B2 и B3 — количество заполнений сеток сохраняется, поскольку мы начинаем с корректной сетки судоку, и единственный способ сохранить корректность в дальнейшем — это поменяить местами B4, B5, B6 и B7, B8, B9 так, как мы поменяли B1, B2, B3. В итоге все стеки останутся теми же самыми. Другими словами, каждое корректное заполнение всей сетки для одной верхней полосы дает ровно одно корректное заполнение сетки для другой верхней полосы, полученной перемешиванием блоков B1, B2, B3.
Упражнение: Убедитесь сами, что если поменять местами блоки B2 и B3 в следующей сетке, то единственный способ сохранить сетку корректной — это поменять местами B5 и B6, а также B8 и B9. Стеки остаются те же самые, но меняются их расположения.
Упражнение: Пусть у вас есть корректно заполненная сетка судоку и вы меняете местами некоторые столбцы в каком либо из блоков B1, B2 или B3. Что нужно дополнительно сделать с остальными столбцами, чтобы сетка судоку осталась корректной? Например, если вы поменяли местами первый и второй столбцы в блоке B2, как бы вы исправили оставшуюся часть сетки так, чтобы она все еще удовлетворяла Главному Правилу?
Последнее упражнение говорит нам о том, что каждое заполнение первой полосы дает нам уникальное заполнение для такой первой полосы, в которой столбцы упорядочены определенным образом внутри блоков.
Это наблюдение позволяет нам уменьшить количество первых полос, которые нам нужно рассмотреть. Согласно Фельгенхауэру и Джарвису, мы перемешиваем столбцы в блоках B2 и B3 таким образом, что значения в самой верхней строке идут в возрастающем порядке. После этого мы возможно меняем местами блоки B2 и B3 так, чтобы самое первое число в блоке B2 (левое верхнее) было меньше, чем самое первое число в блоке B3. Эта операция называется лексикографической редукцией. Поскольку для каждого из двух блоков у нас ровно 6 различных перестановок и всего 2 способа упорядочить блоки друг относительно друга, лексикографическая редукция говорит нам, что для любой первой полосы можно построить класс из 62×2=72 первых полос с одним и тем же количеством полных заполнений сеток (и для всех элементов из каждого класса это построение будет приводить к этому же классу). Таким образом, нам теперь нужно рассмотреть только 2612736/72=36288 первых полос.
Комментарий
Думаю, здесь самое время начать писать код для того, чтобы сделать статью чуть более хардкорной. Мы собираемся проверить, что лексикографически редуцированных верхних полос, в которых блок B1 стандартный — ровно 36288 штук.
Для начала опишем структуру для нашей полосы (я, как обычно, пишу на C++):
В коде пояснений заслуживает разве что метод is_valid(): он проверяет, что Главное Правило для полосы выполняется. Если аргумент with_zeros равен true, то метод не принимает во внимание нули (а нулями мы будем обозначать ячейки частично заполненных полос, в которые пока еще не назначена ни одна цифра).
Код для генерации всех интересующих нас полос выглядит следующим образом:
Сначала мы подготавливаем starting_bands — полосы, в которых заполнен блок B1 и первые строки блоков B2 и B3. Их всего 10 штук, поскольку для поддержания лексикографического порядка мы не учитываем варианты, когда блок B2 «больше» блока B3. После этого мы простеньким перебором находим все искомые полосы. Выкладки, приведенные выше по тексту в коде не используются — они больше для «головы», чем для машины. Главное что числа в итоге сошлись. А сгенерированные полосы мы потом еще будем использовать в следующем спойлере.
Для начала опишем структуру для нашей полосы (я, как обычно, пишу на C++):
struct BAND
{
int m[3][3][3]; // 3 blocks of 3x3 grids
BAND()
{
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
m[i][j][k] = 0;
}
void print()
{
for (int i=0; i<3; i++)
{
for (int j=0; j<3; j++)
{
for (int k=0; k<3; k++)
printf( "%d", m[j][i][k] );
printf( " " );
}
printf( "\n" );
}
printf( "\n" );
}
bool is_valid( bool with_zeros )
{
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
{
if (!(0<=m[i][j][k] && m[i][j][k]<=9)) return false;
if (!with_zeros && m[i][j][k]==0) return false;
}
bool F[10];
for (int i=0; i<3; i++) // check blocks
{
memset( F, 0, sizeof( F ) );
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
{
if (F[m[i][j][k]]) return false;
if (m[i][j][k]>0) F[m[i][j][k]] = true;
}
}
for (int i=0; i<3; i++) // check rows
{
memset( F, 0, sizeof( F ) );
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
{
if (F[m[j][i][k]]) return false;
if (m[j][i][k]>0) F[m[j][i][k]] = true;
}
}
return true;
}
};
В коде пояснений заслуживает разве что метод is_valid(): он проверяет, что Главное Правило для полосы выполняется. Если аргумент with_zeros равен true, то метод не принимает во внимание нули (а нулями мы будем обозначать ячейки частично заполненных полос, в которые пока еще не назначена ни одна цифра).
Код для генерации всех интересующих нас полос выглядит следующим образом:
void gen_bands( BAND band, int block, int row, int col, vector< BAND > & res )
{
col++; // move to the next empty cell
if (col==3) { col=0; row++; }
if (row==3) { row=1; block++; }
if (block==3) // no next empty cell
{
res.push_back( band );
return;
}
for (int a=1; a<=9; a++)
{
band.m[block][row][col] = a;
if (band.is_valid( true ))
gen_bands( band, block, row, col, res );
}
}
vector< BAND > gen_all_bands()
{
BAND b0;
int t=1;
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
b0.m[0][i][j] = t++;
// b0 has standard block B1; B2 and B3 are empty
vector< BAND > starting_bands;
for (int a=4; a<=4; a++)
for (int b=a+1; b<=9; b++)
for (int c=b+1; c<=9; c++)
{
BAND b1 = b0;
b1.m[1][0][0] = a;
b1.m[1][0][1] = b;
b1.m[1][0][2] = c;
int ind = 0;
for (int d=4; d<=9; d++)
if (d!=a && d!=b && d!=c)
b1.m[2][0][ind++] = d;
//b1.print();
starting_bands.push_back( b1 );
}
// we filled the first row by all possible ways
printf( "bands with filled the first row %d\n", (int)starting_bands.size() ); // 10 bands total
vector< BAND > reduced_bands;
for (int i=0; i<(int)starting_bands.size(); i++)
gen_bands( starting_bands[i], 0, 2, 2, reduced_bands );
printf( "lexicographically reduced bands %d\n", (int)reduced_bands.size() ); // 36288 bands total
return reduced_bands;
}
Сначала мы подготавливаем starting_bands — полосы, в которых заполнен блок B1 и первые строки блоков B2 и B3. Их всего 10 штук, поскольку для поддержания лексикографического порядка мы не учитываем варианты, когда блок B2 «больше» блока B3. После этого мы простеньким перебором находим все искомые полосы. Выкладки, приведенные выше по тексту в коде не используются — они больше для «головы», чем для машины. Главное что числа в итоге сошлись. А сгенерированные полосы мы потом еще будем использовать в следующем спойлере.
Для каждого из этих вариантов рассмотрим всевозможные перестановки трех верхних блоков: их ровно 6. А для каждого из этих вариантов имеется 63 перестановок столбцов внутри всех блоков. После того, как мы все перемешали, вы переназначаем числа так, чтобы в блоке B1 они все шли в стандартном порядке. Мы также можем произвольно перемешать три верхние строки, после чего опять переназначить числа, чтобы блок B1 стал стандартным. После каждой из этих операций количество заполнение всей сетки для данной первой полосы останется неизменным. Фельгенхауэр и Джарвис при помощи компьютерной программы определили, что эти операции сокращают количество первых полос, которые имеет смысл рассматривать, с 36288 до всего лишь 416.
Упражнение: Рассмотрите определенную первую полосу. Проделайте над ней некоторые операции, которые сохраняют количество заполнений всей сетки судоку. Можете начать со следующего: поменяйте местами первую и вторую строки. После этого переназначьте числа в блоке B1, чтобы привести его к стандартной форме. Выполните лексикографическую редукцию.
Главное, на что следует обратить внимание: полоса, с которой мы начали, и полоса, которой закончили, имеют одинаковое количество заполнения всей сетки судоку. Поэтому вместо вычисления количества заполнений сеток для каждой полосы мы можем подсчитывать их количество только для одной из них.
Комментарий
Начиная с этого момента начинаются некоторые неочевидности — авторы оригинал предлагают поверить им наслово. Но мы не такие — мы будем писать код для того, чтобы удостовериться лично. А именно: сейчас мы будем проверять тот факт, что выполняя описанные выше операции, мы в итоге получим ровно 416 вариантов.
Для большей наглядности опишем что же мы сейчас будем делать: мы будем строить граф. Представьте себе, что каждая из лексикографически редуцированных полос — это вершина графа (т.е. у нас всего 36288 вершин). Когда мы применяем к полосе какую либо операцию (которая перемешивает числа, но не меняет количество итоговых сеток для данной полосы) — мы в нашем графе соединяем ребром начальную полосу и конечную. Ребра неориентированные, поскольку каждая из рассмотренных выше операций обратима — мы можем вернуть все взад делая действия в обратном порядке. Теперь давайте для каждой полосы применим всевозможные операции и проведем всевозможные ребра. Тогда, для любых двух вершин, соединенных цепочкой ребер, ответ будет одинаковый. Да и вообще — он будет один и тот же для всех вершин в одной компоненте связности. То есть, нам нужно посчитать количество компонент связности в полученном графе — и их должно оказаться ровно 416.
Сначала внесем модификации в структуру BAND:
Теперь мы можем нашу полосу лексикографически редуцировать (метод normalize()), а также делать все 3 операции, описанные выше. При применении операции создается копия объекта, затем к копии применяется операция, затем результат нормализуется (чтобы не выходить за пределы редуцированных 36288 полос).
Теперь мы можем посчитать количество компонент связности при помощи стандартного обхода в глубину. При этом граф явно не строится.
Операторы сравнения нужны для того, чтобы их мог использовать set. В итоге программа действительно находит ровно 416 компонент связности. В comp_sizes складываются размеры этих компонент, а в ident_bands — одна из вершин из каждой компоненты (полоса — представитель класса). Следует отметить, что получаемые компоненты не всегда имеют одинаковый размер. Например, программа выводит следующие размеры:
Ну и теперь, по сути, можно посчитать количество итоговых заполнений для каждого представителя, умножить на количество вершин в соответствующей компоненте и в конце все сложить. Но с этим пока не будем торопиться.
Для большей наглядности опишем что же мы сейчас будем делать: мы будем строить граф. Представьте себе, что каждая из лексикографически редуцированных полос — это вершина графа (т.е. у нас всего 36288 вершин). Когда мы применяем к полосе какую либо операцию (которая перемешивает числа, но не меняет количество итоговых сеток для данной полосы) — мы в нашем графе соединяем ребром начальную полосу и конечную. Ребра неориентированные, поскольку каждая из рассмотренных выше операций обратима — мы можем вернуть все взад делая действия в обратном порядке. Теперь давайте для каждой полосы применим всевозможные операции и проведем всевозможные ребра. Тогда, для любых двух вершин, соединенных цепочкой ребер, ответ будет одинаковый. Да и вообще — он будет один и тот же для всех вершин в одной компоненте связности. То есть, нам нужно посчитать количество компонент связности в полученном графе — и их должно оказаться ровно 416.
Сначала внесем модификации в структуру BAND:
struct BAND
{
/* old code */
void normalize() // turn into standard form
{
// relabeling
int relabel[10];
int t = 1;
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
relabel[m[0][i][j]] = t++;
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
m[i][j][k] = relabel[m[i][j][k]];
// lexicographic reduction
for (int i=1; i<3; i++)
{
if (m[i][0][0] > m[i][0][1])
for (int j=0; j<3; j++)
swap( m[i][j][0], m[i][j][1] );
if (m[i][0][1] > m[i][0][2])
for (int j=0; j<3; j++)
swap( m[i][j][1], m[i][j][2] );
if (m[i][0][0] > m[i][0][1])
for (int j=0; j<3; j++)
swap( m[i][j][0], m[i][j][1] );
}
// swap B2 and B3
if (m[1][0][0] > m[2][0][0])
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
swap( m[1][i][j], m[2][i][j] );
}
BAND get_copy()
{
BAND re;
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
re.m[i][j][k] = m[i][j][k];
return re;
}
BAND swap_blocks( int x, int y ) // swap blocks x and y
{
BAND re = get_copy();
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
swap( re.m[x][i][j], re.m[y][i][j] );
re.normalize();
return re;
}
BAND swap_rows( int x, int y ) // swap rows x and y
{
BAND re = get_copy();
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
swap( re.m[i][x][j], re.m[i][y][j] );
re.normalize();
return re;
}
BAND swap_columns( int b, int x, int y ) // swap columns x and y in block b
{
BAND re = get_copy();
for (int i=0; i<3; i++)
swap( re.m[b][i][x], re.m[b][i][y] );
re.normalize();
return re;
}
};
Теперь мы можем нашу полосу лексикографически редуцировать (метод normalize()), а также делать все 3 операции, описанные выше. При применении операции создается копия объекта, затем к копии применяется операция, затем результат нормализуется (чтобы не выходить за пределы редуцированных 36288 полос).
Теперь мы можем посчитать количество компонент связности при помощи стандартного обхода в глубину. При этом граф явно не строится.
bool operator< ( const BAND & A, const BAND & B )
{
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
if (A.m[i][j][k] != B.m[i][j][k])
return A.m[i][j][k] < B.m[i][j][k];
return false;
}
bool operator== ( const BAND & A, const BAND & B )
{
for (int i=0; i<3; i++)
for (int j=0; j<3; j++)
for (int k=0; k<3; k++)
if (A.m[i][j][k] != B.m[i][j][k])
return false;
return true;
}
set< BAND > used_bands;
int comp_size;
void dfs( BAND b )
{
if (used_bands.find( b ) != used_bands.end()) return;
comp_size++;
used_bands.insert( b );
for (int i=0; i<3; i++)
for (int j=i+1; j<3; j++)
{
dfs( b.swap_blocks( i, j ) );
dfs( b.swap_rows( i, j ) );
for (int k=0; k<3; k++)
dfs( b.swap_columns( k, i, j ) );
}
}
void solution()
{
vector< BAND > bands = gen_all_bands();
vector< int > comp_sizes;
vector< BAND > ident_bands;
for (int i=0; i<(int)bands.size(); i++)
if (used_bands.find( bands[i] ) == used_bands.end())
{
comp_size = 0;
dfs( bands[i] );
comp_sizes.push_back( comp_size );
ident_bands.push_back( bands[i] );
}
printf( "number of connected components %d\n", (int)comp_sizes.size() ); // 416 components
for (int i=0; i<(int)comp_sizes.size(); i++)
printf( "%d ", comp_sizes[i] );
}
Операторы сравнения нужны для того, чтобы их мог использовать set. В итоге программа действительно находит ровно 416 компонент связности. В comp_sizes складываются размеры этих компонент, а в ident_bands — одна из вершин из каждой компоненты (полоса — представитель класса). Следует отметить, что получаемые компоненты не всегда имеют одинаковый размер. Например, программа выводит следующие размеры:
1 27 18 54 6 9 54 108 9 54 108 54 54 108 54 54 54 18 6 108 54 54 6 18 6 54 18 54 18 54 2 54 108 108 108 54 108 108 108 108 54 108 108 108 54 108 108 54 108 54 108 54 108 108 108 54 108 108 108 54 108 108 108 54 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 54 108 108 108 108 108 108 108 54 108 108 108 108 54 108 108 108 18 108 108 54 108 108 108 54 54 108 108 108 54 54 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 54 108 108 108 108 108 108 108 108 108 108 108 108 108 108 54 54 54 18 54 54 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 54 108 108 108 108 54 108 108 54 108 108 108 108 108 108 108 108 108 36 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 54 108 54 108 108 108 108 108 108 108 54 108 108 108 54 108 108 108 108 54 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 108 54 108 108 54 108 108 108 108 108 54 108 108 108 108 108 108 54 54 54 54 54 54 6 18 54 18 108 54 54 108 54 54 108 54 54 108 108 108 108 54 108 108 108 108 108 54 108 108 108 108 108 108 108 54 54 108 108 108 108 108 54 108 54 108 108 54 54 108 108 108 108 108 108 54 18 18 54 54 108 54 54 108 108 54 108 108 54 108 108 108 108 108 54 108 54 18 54 108 108 54 54 108 108 54 54 108 108 108 54 54 108 108 108 108 108 108 108 54 36 108 108 108 108 108 54 108 108 108 108 108 54 108 108 54 54 108 54 108 108 108 54 54 108 108 108 54 18 108 54 54 54 108 54 18 18 54 54 54 108 18 54 54 54 54 3 27 9 9
Ну и теперь, по сути, можно посчитать количество итоговых заполнений для каждого представителя, умножить на количество вершин в соответствующей компоненте и в конце все сложить. Но с этим пока не будем торопиться.
Существует еще несколько операций, которые сокращают количество сеток для рассмотрения. Если у нас есть пара чисел {a,b} такая, что a и b находятся в одном столбце, причем a — на i-й строке, а b — на j-ой, и, ко всему прочему, есть такая же пара в другом столбце, причем для этого столбца a уже находится на j-ой строке, а b — на i-ой (т.е. эти четыре числа находятся в углах некоторого прямоугольника, и противоположные числа равны), то мы можем поменять местами числа в обеих парах и получить новую корректную полосу с тем же количеством конечных сеток. Например, в судоку, приведенном чуть выше, числа 8 и 9 в шестом и девятом столбцах формируют такую конфигурацию. Рассмотрев все возможные случаи, Фельгенхауэр и Джарвис сократили необходимое для рассмотрения число первых полос с 416 до 174.
Но и это еще не все. Они рассмотрели другие конфигурации одинаковых множеств (из трех и более чисел), лежащих друг напротив друга в двух различных столбцах или строках, которые можно поменять местами и ответ от этого не изменится. Это сокращает количество вариантов до 71, а если дополнительно рассмотреть эти варианты и применить там более сложные симметрии — количество полос для рассмотрения можно сократить до 44. И для каждой из этих 44 полос все остальные полосы в соответствующем классе имеют такое же количество полных заполнений всей сетки.
Комментарий
Давайте дополним нашу программу новыми операциями для того, чтобы получить улучшения до 174 и до 71 полосы. До 44 полос мы улучшать не будем — там все совсем сложно, да и внятной информации об этом очень мало. Фельгенхауэр и Джарвис в своей статье улучшают только до 71, а число 44 они приводят уже в конце после всех вычислений (впрочем, они также пишут, что там есть подходящие преобразования, чтобы получить искомые 44 полосы — об этом в конце данного спойлера).
Итак, завайте добавим операцию свапания двух пар чисел, которые располагаются в углах одного прямоугольника. К уже написанному коду это добавить очень просто:
Мы просто перебираем все прямоугольники (единственная оптимизация — левый и правый столбцы этого прямоугольника должны лежать в различных блоках по понятным причинам) и проверяем, что в противоположных углах одинаковые числа. Если это так — делаем изменение полосы, иначе оставляем полосу неизменной (тогда, фактически, в нашем графе генерирует петля, которая ни на что не влияет).
Если запустить обновленный код — мы получим, как и ожидалось, ровно 174 полосы.
Добавим еще операций:
Первая из операций swap_3x2() — это случай, когда мы ищем одинаковые подмножества в двух столбцах. Дело в том, что подмножество размера 1 не бывает (иначе нарушается Главное Правило), подмножество размера 2 уже обрабатывается процедурой swap_cross(), а всего строк у нас 3. Значит, нам нужно проверять только один вариант — все три числа в двух столбцах. Для них существуют ровно два варианта соответствия:
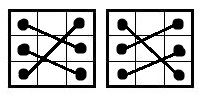
Если все совпало — мы просто меняем местами столбцы. Иначе — оставляем полосу неизменной.
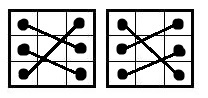
Для второй операции swap_mask() мы перебираем всевозможные подмножества столбцов и смотрим для двух строк — одинаковые ли получаются множества чисел для этих подмножеств столбцов. Примеры подходящих вариантов:
При совпадении мы меняем местами найденные подмножества (свапаем пару в каждом столбце). При несовпадении — ничего не делаем.
Следует отметить, что рассмотренная ранее операция swap_cross() — это частный случай swap_mask(). Поэтому swap_cross() можно вообще выкинуть за ненадобностью.
На этот раз запуск программы будет долгим — на моей машине программа работает около 30 секунд. Но результат тот, что и ожидался — 71. Понятно, что код написан далеко не оптимально, но для наших целей такой производительности хватает более чем.
Размеры компонент связности получаются следующие:
Что же до операций, которые сокращают число вариантов до 44, то они выглядят как-то так:
Можете попробовать описать их более формально и реализовать в коде.
Итак, завайте добавим операцию свапания двух пар чисел, которые располагаются в углах одного прямоугольника. К уже написанному коду это добавить очень просто:
struct BAND
{
/* old code */
BAND swap_cross( int b1, int b2, int r1, int r2, int c1, int c2 )
{
BAND re = get_copy();
// note: b1 must be together with c1 and b2 must be together with c2
if (re.m[b1][r1][c1] == re.m[b2][r2][c2] && re.m[b1][r2][c1] == re.m[b2][r1][c2])
{
swap( re.m[b1][r1][c1], re.m[b2][r1][c2] );
swap( re.m[b1][r2][c1], re.m[b2][r2][c2] );
}
re.normalize();
return re;
}
};
void dfs( BAND b )
{
/* old code */
for (int b1=0; b1<3; b1++)
for (int b2=b1+1; b2<3; b2++)
for (int r1=0; r1<3; r1++)
for (int r2=r1+1; r2<3; r2++)
for (int c1=0; c1<3; c1++)
for (int c2=0; c2<3; c2++)
dfs( b.swap_cross( b1, b2, r1, r2, c1, c2 ) );
}
Мы просто перебираем все прямоугольники (единственная оптимизация — левый и правый столбцы этого прямоугольника должны лежать в различных блоках по понятным причинам) и проверяем, что в противоположных углах одинаковые числа. Если это так — делаем изменение полосы, иначе оставляем полосу неизменной (тогда, фактически, в нашем графе генерирует петля, которая ни на что не влияет).
Если запустить обновленный код — мы получим, как и ожидалось, ровно 174 полосы.
Добавим еще операций:
struct BAND
{
/* old code */
BAND swap_3x2( int b1, int b2, int c1, int c2 )
{
BAND re = get_copy();
// note: b1 must be together with c1 and b2 must be together with c2
if (( re.m[b1][0][c1] == re.m[b2][1][c2] &&
re.m[b1][1][c1] == re.m[b2][2][c2] &&
re.m[b1][2][c1] == re.m[b2][0][c2]) ||
( re.m[b1][0][c1] == re.m[b2][2][c2] &&
re.m[b1][1][c1] == re.m[b2][0][c2] &&
re.m[b1][2][c1] == re.m[b2][1][c2]))
{
swap( re.m[b1][0][c1], re.m[b2][0][c2] );
swap( re.m[b1][1][c1], re.m[b2][1][c2] );
swap( re.m[b1][2][c1], re.m[b2][2][c2] );
}
re.normalize();
return re;
}
BAND swap_mask( int r1, int r2, int mask )
{
BAND re = get_copy();
int num1=0, num2=0;
for (int i=0; i<3; i++) // block
for (int j=0; j<3; j++) // col
if ((mask>>(i*3+j))&1)
{
num1 += (1<<re.m[i][r1][j]);
num2 += (1<<re.m[i][r2][j]);
}
if (num1 == num2)
for (int i=0; i<3; i++) // block
for (int j=0; j<3; j++) // col
if ((mask>>(i*3+j))&1)
swap( re.m[i][r1][j], re.m[i][r2][j] );
re.normalize();
return re;
}
};
void dfs( BAND b )
{
/* old code */
for (int b1=0; b1<3; b1++)
for (int b2=b1+1; b2<3; b2++)
for (int c1=0; c1<3; c1++)
for (int c2=0; c2<3; c2++)
dfs( b.swap_3x2( b1, b2, c1, c2 ) );
for (int r1=0; r1<3; r1++)
for (int r2=r1+1; r2<3; r2++)
for (int mask=1; mask<(1<<9); mask++)
dfs( b.swap_mask( r1, r2, mask ) );
}
Первая из операций swap_3x2() — это случай, когда мы ищем одинаковые подмножества в двух столбцах. Дело в том, что подмножество размера 1 не бывает (иначе нарушается Главное Правило), подмножество размера 2 уже обрабатывается процедурой swap_cross(), а всего строк у нас 3. Значит, нам нужно проверять только один вариант — все три числа в двух столбцах. Для них существуют ровно два варианта соответствия:
Если все совпало — мы просто меняем местами столбцы. Иначе — оставляем полосу неизменной.
Для второй операции swap_mask() мы перебираем всевозможные подмножества столбцов и смотрим для двух строк — одинаковые ли получаются множества чисел для этих подмножеств столбцов. Примеры подходящих вариантов:
При совпадении мы меняем местами найденные подмножества (свапаем пару в каждом столбце). При несовпадении — ничего не делаем.
Следует отметить, что рассмотренная ранее операция swap_cross() — это частный случай swap_mask(). Поэтому swap_cross() можно вообще выкинуть за ненадобностью.
На этот раз запуск программы будет долгим — на моей машине программа работает около 30 секунд. Но результат тот, что и ожидался — 71. Понятно, что код написан далеко не оптимально, но для наших целей такой производительности хватает более чем.
Размеры компонент связности получаются следующие:
4 108 72 216 24 216 216 2592 216 216 1296 1404 540 108 72 510 702 270 2214 6 504 6 1350 666 702 18 756 20 2268 1134 2592 972 270 864 864 972 2052 486 270 1620 540 432 144 432 864 324 540 270 270 234 6 18 540 288 216 54 108 108 288 54 378 108 108 54 108 54 108 36 108 54 54
Что же до операций, которые сокращают число вариантов до 44, то они выглядят как-то так:
Можете попробовать описать их более формально и реализовать в коде.
Пусть C — одна из 44 полос. Тогда количество способов, которым C можно дополнить до полной сетки судоку, обозначим на nC. Нам также понадобится число mC — общее количество полос, для которых количество конечных заполнений такое же, как и у C. Когда общее количество различных судоку будет равно N=ΣCmCnC, то есть сумма mCnC по всем 44 полосам.
Фельгенхауэр и Джарвис написали компьютерную программу для выполнения итоговых рассчетов. Они вычислили число N1 (количество корректных заполнений, в которых B1 в стандартной форме) для каждой из 44 полос. Затем они умножили это число за 9!, чтобы получить ответ. Они обнаружили, что количество всевозможных корректных сеток судоку 9 на 9 равно N=6670903752021072936960, что приблизительно равно 6.671×1021.
Комментарий
Давайте и мы допишем нашу программу для рассчетов. Начнем со структуры GRID — сетки судоку, в которую можно вписывать числа и для каждой пустой ячейки узнавать можно ли в нее записать какое-либо число или нет.
Массивы флагов R, C и B хранят информацию о том, какие числа уже отмечены в соответствующих строках, столбцах и блоках. Это позволяет затем быстро определить можно ли поставить в какую-либо ячейку какое-либо число или нет.
Следующая процедура для каждой полосы BAND строит начальную сетку для перебора GRID и запускает перебор:
На самом деле, данная процедура в самом начале заполняет первый столбец сетки, да не всеми способами, а только лексикографически редуцированными — это сокращает дальнейший перебор ровно в 72 раза (главное потом не забыть домножить ответ на 72). Итого каждый вызов процедуры process_band() запускает dfs2() ровно 10 раз.
Сам же перебор выглядит следующим образом:
Перебор совершенно бесхитростный. Мы перебираем все оставшиеся незаполненные клетки в следующем порядке: сначала идем сверху вниз по второму столбцу (в блоках B4 и B7), затем идем сверху вниз по третьему столбцу и так далее.
Один запуск dfs2() на моей машине работает около 30 секунд, т.е. на обработку одной полосы нужно около 5 минут. Реализацию, конечно же, можно немного ускорить, вы можете попробовать сделать это самостоятельно. Программа Фельгенхауэра и Джарвиса для одной полосы работает около 2 минут (как они пишут в своей статье), т.е. всего в 2,5 раза быстрее нашей реализации. Полная обработка всех 71 полос (для нашей программы) занимает 6 часов.
В результате работы программа выводит следующее:
Для получения финального результата нужно воспользоваться калькулятором (длинную арифметику писать не хотелось), и… все совпадает! Можете сверить числа с теми, что получились у Фельгенхауэра и Джарвиса тут.
Полный код нашей программы (чтобы не собирать кусками из спойлеров) находится тут.
struct GRID
{
int T[9][9];
bool R[9][10], C[9][10], B[9][10];
void clear()
{
memset( T, 0, sizeof( T ) );
memset( R, 0, sizeof( R ) );
memset( C, 0, sizeof( C ) );
memset( B, 0, sizeof( B ) );
}
void print()
{
for (int i=0; i<9; i++)
{
for (int j=0; j<9; j++)
printf( "%d", T[i][j] );
printf( "\n" );
}
printf( "\n" );
}
bool can_set( int num, int x, int y )
{
return !R[x][num] && !C[y][num] && !B[(x/3)*3+(y/3)][num];
}
void set_num( int num, int x, int y )
{
T[x][y] = num;
R[x][num] = true;
C[y][num] = true;
B[(x/3)*3+(y/3)][num] = true;
}
void unset_num( int num, int x, int y )
{
T[x][y] = 0;
R[x][num] = false;
C[y][num] = false;
B[(x/3)*3+(y/3)][num] = false;
}
} G;
Массивы флагов R, C и B хранят информацию о том, какие числа уже отмечены в соответствующих строках, столбцах и блоках. Это позволяет затем быстро определить можно ли поставить в какую-либо ячейку какое-либо число или нет.
Следующая процедура для каждой полосы BAND строит начальную сетку для перебора GRID и запускает перебор:
long long process_band( BAND band )
{
int nums[] = { 2, 3, 5, 6, 8, 9 };
long long res = 0;
for (int i=1; i<6; i++)
for (int j=i+1; j<6; j++)
{
G.clear();
for (int a=0; a<3; a++)
for (int b=0; b<3; b++)
for (int c=0; c<3; c++)
G.set_num( band.m[a][b][c], b, a*3+c );
G.set_num( nums[0], 3, 0 );
G.set_num( nums[i], 4, 0 );
G.set_num( nums[j], 5, 0 );
int t = 6;
for (int k=1; k<6; k++)
if (k!=i && k!=j)
G.set_num( nums[k], t++, 0 );
// starting grid is complete
//G.print();
grids_count = 0;
dfs2( 8, 0 );
res += grids_count;
fprintf( stderr, "." );
}
return res;
}
На самом деле, данная процедура в самом начале заполняет первый столбец сетки, да не всеми способами, а только лексикографически редуцированными — это сокращает дальнейший перебор ровно в 72 раза (главное потом не забыть домножить ответ на 72). Итого каждый вызов процедуры process_band() запускает dfs2() ровно 10 раз.
Сам же перебор выглядит следующим образом:
int grids_count;
void dfs2( int x, int y )
{
x++; // find next empty cell
if (x==9) { x=3; y++; }
if (y==9) // no empty cells
{
grids_count++;
return;
}
for (int a=1; a<=9; a++)
if (G.can_set( a, x, y ))
{
G.set_num( a, x, y );
dfs2( x, y );
G.unset_num( a, x, y );
}
}
Перебор совершенно бесхитростный. Мы перебираем все оставшиеся незаполненные клетки в следующем порядке: сначала идем сверху вниз по второму столбцу (в блоках B4 и B7), затем идем сверху вниз по третьему столбцу и так далее.
Один запуск dfs2() на моей машине работает около 30 секунд, т.е. на обработку одной полосы нужно около 5 минут. Реализацию, конечно же, можно немного ускорить, вы можете попробовать сделать это самостоятельно. Программа Фельгенхауэра и Джарвиса для одной полосы работает около 2 минут (как они пишут в своей статье), т.е. всего в 2,5 раза быстрее нашей реализации. Полная обработка всех 71 полос (для нашей программы) занимает 6 часов.
В результате работы программа выводит следующее:
bands with filled the first row 10
lexicographically reduced bands 36288
number of connected components 71
0/71 4 x 108374976
1/71 108 x 102543168
2/71 72 x 100231616
3/71 216 x 99083712
4/71 24 x 97282720
5/71 216 x 102047904
6/71 216 x 98875264
7/71 2592 x 98733568
8/71 216 x 98875264
9/71 216 x 99525184
10/71 1296 x 98369440
11/71 1404 x 97287008
12/71 540 x 98128064
13/71 108 x 98128064
14/71 72 x 97685328
15/71 510 x 98950072
16/71 702 x 98153104
17/71 270 x 97961464
18/71 2214 x 97961464
19/71 6 x 98950072
20/71 504 x 97685328
21/71 6 x 99258880
22/71 1350 x 97477096
23/71 666 x 97549160
24/71 702 x 97477096
25/71 18 x 97549160
26/71 756 x 96702240
27/71 20 x 94888576
28/71 2268 x 97116296
29/71 1134 x 98371664
30/71 2592 x 97539392
31/71 972 x 97910032
32/71 270 x 98493856
33/71 864 x 98119872
34/71 864 x 98733184
35/71 972 x 97116296
36/71 2052 x 96482296
37/71 486 x 97346960
38/71 270 x 97346960
39/71 1620 x 97416016
40/71 540 x 97455648
41/71 432 x 98784768
42/71 144 x 101131392
43/71 432 x 97992064
44/71 864 x 97756224
45/71 324 x 96380896
46/71 540 x 97910032
47/71 270 x 97416016
48/71 270 x 97714592
49/71 234 x 96100688
50/71 6 x 99258880
51/71 18 x 96100688
52/71 540 x 96482296
53/71 288 x 96807424
54/71 216 x 97372400
55/71 54 x 97714592
56/71 108 x 97372400
57/71 108 x 95596592
58/71 288 x 96631520
59/71 54 x 95596592
60/71 378 x 95596592
61/71 108 x 96482296
62/71 108 x 96482296
63/71 54 x 98371664
64/71 108 x 97455648
65/71 54 x 97416016
66/71 108 x 97287008
67/71 36 x 97372400
68/71 108 x 98048704
69/71 54 x 98493856
70/71 54 x 98153104
total number of sudoku 3546146300288*9!*72*72
total time 21213 sec
Для получения финального результата нужно воспользоваться калькулятором (длинную арифметику писать не хотелось), и… все совпадает! Можете сверить числа с теми, что получились у Фельгенхауэра и Джарвиса тут.
Полный код нашей программы (чтобы не собирать кусками из спойлеров) находится тут.
Продолжение следует
В следующей части мы посчитаем количество действительно различных судоку, считая что два судоку одинаковые, если они переходят друг в друга поворотами, отражениями, перемешиванием столбцов и так далее. Для этого мы погрузимся в теорию групп, познакомимся с леммой Бернсайда и, конечно же, напишем аццкую программу для подсчета ответа. В общем, не пропустите.








