
На мой взгляд, стохастические исчисления — это один из тех великолепных разделов высшей математики (наряду с топологией и комплексным анализом), где формулы встречаются с поэзией; это место, где они обретают красоту, место где начинается простор для художественного творчества. Многие из тех, что прочли статью Винеровский хаос или Еще один способ подбросить монетку, даже если и мало, что поняли, всё же смогли оценить великолепие этой теории. Сегодня мы с вами продолжим наше математическое путешествие, мы погрузимся в мир случайных процессов, нетривиального интегрирования, финансовой математики и даже немного коснемся функционального программирования. Предупреждаю, держите наготове свои извилины, так как разговор у нас предстоит серьезный.

Кстати, если вам интересно прочитать в отдельной статье, как вдруг оказалось, что
Скрытая угроза фракталов
Представьте себе какую-нибудь простую функцию
К тому моменту как Бенуа Мандельброт придумал само понятие «фракталов», они уже сотню лет не давали спать многим мировым ученым. Одним из первых, кому фракталы подмочили репутацию, стал Андре-Мари Ампер. В 1806 году ученый выдвинул довольно убедительное «доказательство» того, что любую функцию можно разбить на интервалы из непрерывных функций, а те в свою очередь, благодаря непрерывности, должны иметь производную. И многие его современники-математики с ним согласились. Вообще, Ампера нельзя винить в этой, с виду довольно грубой, ошибке. Математики начала XIX века имели довольно расплывчатое определение таких ныне столь базовых концепций мат.анализа как непрерывность и дифференцируемость, и, как следствие, могли сильно ошибаться в своих доказательствах. Не исключением были даже такие именитые ученые как Гаусс, Фурье, Коши, Лежандр, Галуа, не говоря уже о куда менее известных математиках тех времен.
Тем не менее, в 1872 году гипотезу о существовании производных у непрерывных функций опроверг Карл Вейерштрасс, представив на обозрение первого в мире фрактального монстра, всюду непрерывного и нигде не дифференцируемого.
Вот, к примеру, как задается подобная функция:
Таким же свойством обладает и Броуновское движение (кстати, почему-то не Брауновское, фамилия-то британская, всё же). Броуновское движение — это непрерывный случайный процесс
Бесконечная вариация Броуновского движения
Давайте снова представим себе функцию

будет конечной. В каком случае мы не столь уверены? Ну, например, конечной вариации не будет у функции
Вот, как будет выглядеть довольно простая реализация вариации на Хаскеле:
-- | 'totalVariation' calculates total variation of the sample process X(t)
totalVariation :: [Double] -- process trajectory X(t)
-> Double -- V(X(t))
totalVariation x@(_:tx) = sum $ zipWith (\x xm1 -> abs $ x - xm1) tx x
Где в реальном мире встречаются случайные процессы? Один из известнейших примеров сегодня — финансовые рынки, а именно движение цен на валюту, акции, опционы и различные ценные бумаги. Пускай
Теперь мы с легкостью можем что-нибудь проинтегрировать. Возьмем траекторию какого-нибудь непрерывного случайного процесса и обзовём её

Итак вопрос: можно ли взять интеграл в смысле Лебега от Броуновского движения? Посчитаем вариацию, и если она будет конечной, то у нас не должно быть никаких проблем. Давайте зайдем со стороны так называемой квадратичной вариации:
Заметьте, что
Напишем код, считающий квадратичную вариацию реализации случайного процесса
-- | 'quadraticVariation' calculates quadratic variation of the sample process X(t)
quadraticVariation :: [Double] -- process trajectory X(t)
-> Double -- [X(t)]
quadraticVariation x@(_:tx) = sum $ zipWith (\x xm1 -> (x - xm1) ^ 2) tx x
Итак, теперь мы готовы вернуться к подсчету интересующей нас вариации
Мы знаем, что Броуновское движение — процесс непрерывный, а значит
Н-да…

Интеграл Ито или Новая надежда
В 1827 году английский ботаник Роберт Браун, наблюдая пыльцевые зерна в воде через микроскоп, заметил, что частицы внутри их полости двигаются определенным образом; однако он тогда не смог определить механизмы, вызывавшие это движение. В 1905 году Альберт Эйнштейн опубликовал статью, в которой подробно объясняется, как движение, наблюдаемое Брауном, было результатом того, что пыльца перемещается отдельными молекулами воды. В 1923 году вундеркинд и «отец кибернетики» Норберт Винер написал статью о дифференцируемых пространствах, где подошел к этому движению со стороны математики, определил вероятностные меры в пространстве траекторий и, используя концепцию интегралов Лебега, заложил фундамент стохастического анализа. С тех пор в математическом сообществе Броуновское движение также именуется Винеровским процессом.
В 1938 году выпускник Токийского университета Киёси Ито начинает работать в Бюро по статистике, где в свободное время знакомится с работами основателя современной теории вероятности Андрея Колмогорова и французского ученого Поля Леви, изучающего на тот момент различные свойства Броуновского движения. Он пытается соединить воедино интуитивные видения Леви с точной логикой Колмогорова, и в 1942 году пишет работу «О стохастических процессах и бесконечно делимых законах распределения», в которой реконструирует с нуля концепцию стохастических интегралов и связанную с ней теорию стохастических дифференциальных уравнений, описывающих движения, вызванные случайными событиями.
Интеграл Ито для простых процессов
Ито разработал довольно простой способ построения интеграла. Для начала мы определим интеграл Ито для простого кусочно-постоянного процесса

Представим, что
У этого интеграла есть несколько интересных свойств. Первое и довольно очевидное: в начальный момент его математическое ожидание в любой точке равно нулю:
Расчет второго момента/дисперсии уже требует дополнительных расчётов. Пускай
И, наконец, квадратичная вариация. Давайте сначала посчитаем вариацию на каждом интервале
Теперь мы можем ясно видеть разницу между дисперсией и вариацией. Если процесс
Интеграл Ито для сложных процессов
Теперь мы готовы расширить понятие интеграла Ито на более сложные процессы. Пускай у нас есть функция
Для того, чтобы определить
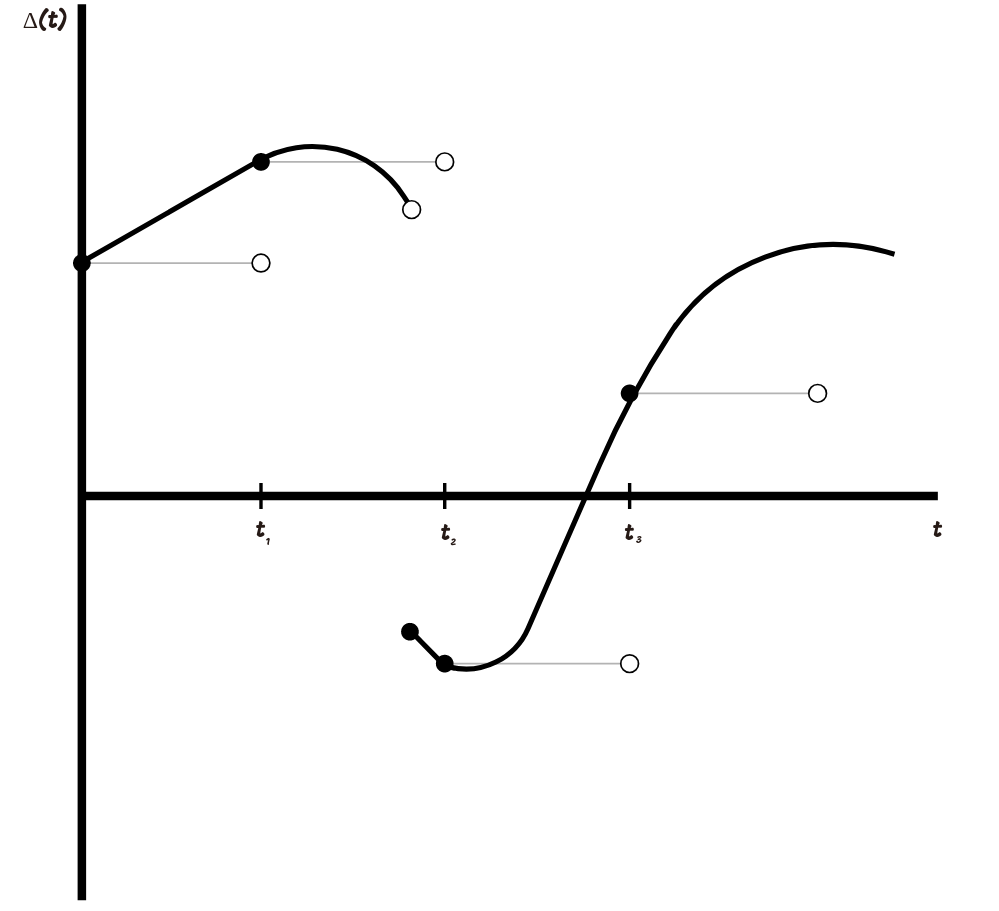
Аппроксимация происходит следующим образом: мы выбираем разбиение
В общем случае, возможно выбрать последовательность простых процессов
- Его траектории непрерывны
- Он адаптирован. Логично, ведь в каждый момент времени мы должны знать наше значение дохода.
- Он линеен:
- Он мартингал, но об этом ближе к концу статьи.
- Сохраняется изометрия Ито:
.
- Его квадратичная вариация:
Небольшая ремарка: для тех, кто хочет более подробно изучить конструирование интеграла Ито или вообще увлекается финансовой математикой, очень советую книгу Steven Shreve «Stochastic Calculus for Finance. Volume II».
Покодим?
Для последующих рассуждений мы будем обозначать интеграл Ито в несколько ином виде:
В предыдущей статье мы реализовали Гауссовский процесс:
data L2Map = L2Map {norm_l2 :: Double -> Double}
type ItoIntegral = Seed -- ω, random state
-> Int -- n, sample size
-> Double -- T, end of the time interval
-> L2Map -- h, L2-function
-> [Double] -- list of values sampled from Ito integral
-- | 'itoIntegral'' trajectory of Ito integral on the time interval [0, T]
itoIntegral' :: ItoIntegral
itoIntegral' seed n endT h = 0 : (toList $ gp !! 0)
where gp = gaussianProcess seed 1 (n-1) (\(i, j) -> norm_l2 h $ fromIntegral (min i j + 1) * t)
t = endT / fromIntegral n
Функция itoIntegral' принимает на вход seed — параметр для генератора случайных величин, n — размерность выходного вектора, endT — параметр
-- | 'mapOverInterval' map function f over the interval [0, T]
mapOverInterval :: (Fractional a) => Int -- n, size of the output list
-> a -- T, end of the time interval
-> (a -> b) -- f, function that maps from fractional numbers to some abstract space
-> [b] -- list of values f(t), t \in [0, T]
mapOverInterval n endT fn = [fn $ (endT * fromIntegral i) / fromIntegral (n - 1) | i <- [0..(n-1)]]
-- | 'itoIntegral' faster implementation of itoIntegral' function
itoIntegral :: ItoIntegral
itoIntegral seed 0 _ _ = []
itoIntegral seed n endT h = scanl (+) 0 increments
where increments = toList $ (sigmas hnorms) * gaussianVector
gaussianVector = flatten $ gaussianSample seed (n-1) (vector [0]) (H.sym $ matrix 1 [1])
sigmas s@(_:ts) = fromList $ zipWith (\x y -> sqrt(x-y)) ts s
hnorms = mapOverInterval n endT $ norm_l2 h
Теперь с помощью этой функции, мы можем реализовать, например, обыкновенное Броуновское движение:
l2_1 = L2Map {norm_l2 = id}
-- | 'brownianMotion' trajectory of Brownian motion a.k.a. Wiener process on the time interval [0, T]
brownianMotion :: Seed -- ω, random state
-> Int -- n, sample size
-> Double -- T, end of the time interval
-> [Double] -- list of values sampled from Brownian motion
brownianMotion seed n endT = itoIntegral seed n endT l2_1
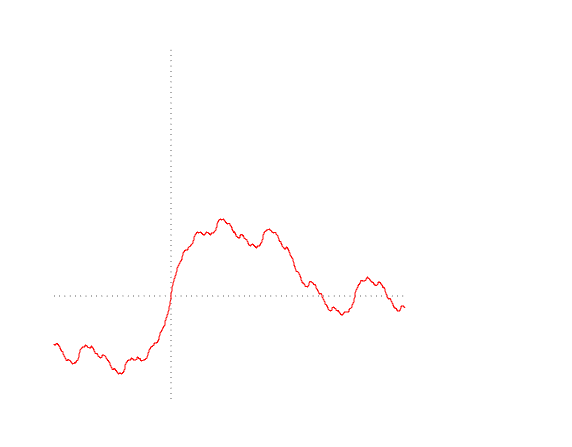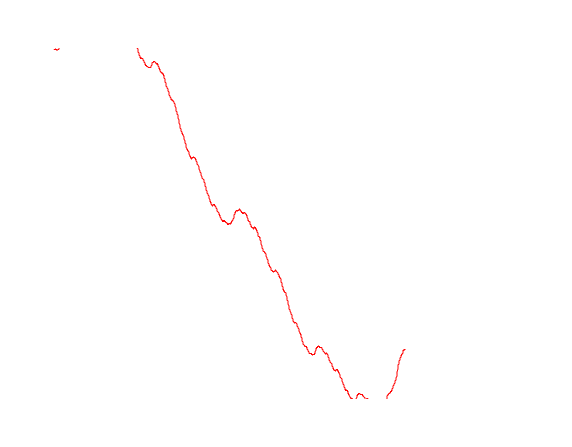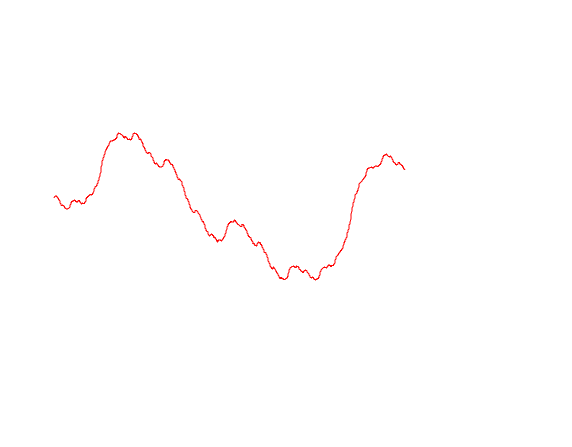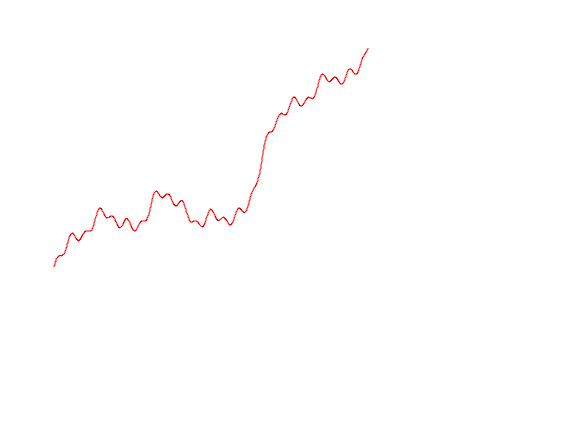
Попробуем нарисовать различные варианты траекторий Броуновского движения
import Graphics.Plot
let endT = 1
let n = 500
let b1 = brownianMotion 1 n endT
let b2 = brownianMotion 2 n endT
let b3 = brownianMotion 3 n endT
mplot [linspace n (0, lastT), b1, b2, b3]

Самое время перепроверить наши предыдущие вычисления. Давайте посчитаем вариацию траектории Броуновского движения на интервале
Prelude> totalVariation (brownianMotion 1 100 1)
8.167687948236862
Prelude> totalVariation (brownianMotion 1 10000 1)
80.5450335433388
Prelude> totalVariation (brownianMotion 1 1000000 1)
798.2689137110999
Мы можем наблюдать, что при увеличении точности вариация принимает все большие и большие значения, в то время как квадратичная вариация стремится к
Prelude> quadraticVariation (brownianMotion 1 100 1)
0.9984487348804609
Prelude> quadraticVariation (brownianMotion 1 10000 1)
1.0136583395467458
Prelude> quadraticVariation (brownianMotion 1 1000000 1)
1.0010717246843375
Попробуйте позапускать вычисления вариаций для произвольных интегралов Ито, чтобы убедиться в том, что
Мартингалы
Есть такой класс случайных процессов — мартингалы. Для того, чтобы
- Он адаптирован
-
почти всюду конечно:
- Условное математическое ожидание будущего значения
равняется его последнему известному значению:
Броуновское движение — мартингал. Выполнение первого условия очевидно, выполнение второго условия следует из свойств нормального распределения. Третье условие также легко проверяется:
Есть еще одна интересная теорема, так называемая теорема о представлении мартингала: если у нас есть мартингал
А на сегодня всё.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Стоит ли рассказать про лемму Ито-Деблина?
95.87% Да, определенно стоит!116
4.13% Нет, это всё не формат Хабра5
Проголосовал 121 пользователь. Воздержались 25 пользователей.






