
В типичной реализации генетический алгоритм оперирует параметрами какой-то сложной функции (диофантовые уравнения в статье "Генетический алгоритм. Просто о сложном" mrk-andreev) или алгоритма ("Эволюция гоночных автомобилей на JavaScript" ilya42). Количество параметров неизменно, операции над ними тоже изменить невозможно, как генетика не старается, потому что они заданы нами.
Хьюстон, у нас проблема
Сложилась странная ситуация — прежде чем применять генетические алгоритмы (ГА) к реальной задаче, мы сначала должны найти алгоритм, которым эта задача в принципе решается, и только потом его попытаться оптимизировать с помощью генетического алгоритма. Если мы ошиблись с выбором «основного» алгоритма, то генетика не найдет оптимум и не скажет, в чем ошибка.
Часто, а в последнее время и модно, вместо детерминированного алгоритма использовать нейронную сеть. Тут у нас тоже открывается широчайший выбор (FNN, CNN, RNN, LTSM, ...), но проблема остается той же — выбрать нужно правильно. Согласно Википедии "Выбирать тип сети следует, исходя из постановки задачи и имеющихся данных для обучения".
А что, если...? Если заставить ГА не оптимизировать параметры, а создавать другой алгоритм, наиболее подходящий для данной задачи. Вот этим я и занимался ради интереса.

Генотип из операций
Напомню, что генетические алгоритмы обычно оперируют т.н. «генотипом», вектором «генов». Для самого ГА не имеет значения, чем будут являться эти гены — числами, буквами, строками или аминокислотами. Важно лишь соблюдение необходимых действий над генотипами — скрещивание, мутация, селекция — необязательно в этом порядке.
Так вот, идея в том, что «геном» будет элементарная операция, а «генотипом» — алгоритм, составленный из этих операций. Например, генотип, составленный из математических операций и реализующий функцию
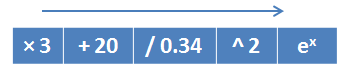
Тогда в результате выполнения ГА мы получим формулу или алгоритм, структуру которого мы заранее предсказать не можем.
Скрещивание фактически не меняется, новый генотип получает кусочки от каждого родителя.
Мутацией может быть замена одного из генов на какой-либо другой, то есть происходит замена одной операции в алгоритме и/или изменение параметров этой операции.
С селекцией и просто, и сложно одновременно. Поскольку мы создаем алгоритм, то самый простой способ его проверить — это выполнить его и оценить полученный результат. Так машинки своим продвижением по трассе доказывали оптимальность своей архитектуры. Но у машинок был четкий критерий — чем дальше она проехала, тем лучше. Наш же целевой алгоритм в общем случае может иметь несколько критериев оценки — длина (чем короче, тем лучше), требования к памяти (чем меньше, тем лучше), устойчивость к мусору на входе и т.д.

Кстати, у машинок критерий был один, но работал он только в пределах текущей трассы. Лучшая для одной трассы машинка вряд ли оказалась бы лучшей на другой.
А если подумать?
В процессе обдумывания, какие операции включить в словарь генов и как они должны работать, я понял, что нельзя ограничиваться операциями над одной переменной. Те же нейронные сети оперируют всеми (FNN) или несколькими (CNN) входными переменными одновременно, поэтому нужен способ задействовать в полученном алгоритме нужное количество переменных. Причем в какой операции какая переменная потребуется, я заранее предугадать не могу и не хочу ограничивать.
На помощь пришел… не угадаете… язык Forth. Точнее, обратная польская запись и стековая машина с их возможностью класть значения переменных на стек и выполнять операции над ними в нужном порядке. И без скобок.
Для стековой машины помимо арифметических операций нужно запрограммировать стековые операции — push (взять следующее значение со входного потока и положить на стек), pop (взять значение со стека и выдать в качестве результата), dup (сдублировать верхнее значение на стеке).
Просто do it!
Получился такой объект, реализующий один ген.
Объект Gen
class Gen():
func = 0
param = ()
def __init__(self):
super().__init__()
self.func = random.randint(0,7)
self.param = round(random.random()*2-1,2)
def calc(self, value, mem):
if self.func == 0: # push
mem.append(value + self.param)
return (None, 1)
elif self.func == 1: # pop
return (mem.pop() + self.param, 0)
elif self.func == 2: # dup
mem.append(mem[-1] + self.param)
return (None, 0)
elif self.func == 3: # add
mem.append(mem.pop() + value + self.param)
return (None, 1)
elif self.func == 4: # del
mem.append(mem.pop() - (value + self.param))
return (None, 1)
elif self.func == 5: # mul
mem.append(mem.pop() * (value + self.param))
return (None, 1)
elif self.func == 6: # div
mem.append(mem.pop() / (value + self.param))
return (None, 1)
return (self.params, 0)
def funcName(self, func):
if self.func >= 0 and self.func <= 7:
return [
'push',
'pop',
'dup',
'add',
'del',
'mul',
'div',
'const'][func]
return str(func)
def __str__(self):
return "%s:%s" % (self.funcName(self.func), str(self.param))
Это был первый вариант, в принципе рабочий, но с ним быстро выявилась проблема — для арифметических операций требовалось передавать значение, а для операций на стеке pop и dup — нет. Мне не хотелось различать вызываемые операции в вызывающем коде и определять, сколько нужно параметров передавать каждой из них, поэтому переделал — вместо одного значения value передавал массив входных значений, и пусть сама операция делает с ним что хочет.
Объект Gen v.2
class Gen():
func = 0
param = ()
def __init__(self):
super().__init__()
self.func = random.randint(0,7)
self.param = round(random.random()*2-1,2)
def calc(self, values, mem):
if self.func == 0: # pop
return mem.pop() + self.param
elif self.func == 1: # push
mem.append(values.pop() + self.param)
return None
elif self.func == 2: # dup
mem.append(mem[-1] + self.param)
return None
elif self.func == 3: # add
mem.append(mem.pop() + values.pop() + self.param)
return None
elif self.func == 4: # del
mem.append(mem.pop() - (values.pop() + self.param))
return None
elif self.func == 5: # mul
mem.append(mem.pop() * (values.pop() + self.param))
return None
elif self.func == 6: # div
mem.append(mem.pop() / (values.pop() + self.param))
return None
return self.param
def funcName(self, func):
if self.func >= 0 and self.func <= 7:
return [
'pop',
'push',
'dup',
'add',
'del',
'mul',
'div',
'const'][func]
return str(func)
def __str__(self):
return "%s:%s" % (self.funcName(self.func), str(self.param))
Второй проблемой стало то, что арифметические операции оказались слишком требовательны — им нужно было и значение на стеке, и входное значение. В результате генетический алгоритм не мог сформировать ни один генотип. Пришлось разделить операции на работающие со стеком и на работающие с входным значением.
Ниже последняя версия.
Объект Gen v.8
class Gen():
func = 0
param = ()
def __init__(self, func=None):
super().__init__()
if func is None:
funcMap = [0,1,2,3,4,5,6,7,8,9,10,11]
i = random.randint(0,len(funcMap)-1)
func = funcMap[i]
self.func = func
self.param = round((random.random()-0.5)*10,2)
def calc(self, values, mem):
def getVal():
v = values[0]
values[0:1]=[]
return v
if self.func == 0: # pop
return mem.pop()
elif self.func == 1: # push
mem.append(getVal())
return None
elif self.func == 2: # dup
mem.append(mem[-1] + self.param)
return None
elif self.func == 3: # addVal
mem.append(getVal() + self.param)
return None
elif self.func == 4: # delVal
mem.append(getVal() + self.param)
return None
elif self.func == 5: # mulVal
mem.append(getVal() * self.param)
return None
elif self.func == 6: # divVal
mem.append(getVal() / self.param)
return None
elif self.func == 7: # addMem
mem.append(self.param + mem.pop())
return None
elif self.func == 8: # delMem
mem.append(self.param - mem.pop())
return None
elif self.func == 9: # mulMem
mem.append(self.param * mem.pop())
return None
elif self.func == 10: # divMem
mem.append(self.param / mem.pop())
return None
mem.append(self.param)
return None
def funcName(self, func):
funcNames = (
'pop',
'push',
'dup',
'addVal',
'delVal',
'mulVal',
'divVal',
'addMem',
'delMem',
'mulMem',
'divMem',
'const')
if self.func >= 0 and self.func < len(funcNames):
return funcNames[func]
return str(func)
def __str__(self):
return "%s:%s" % (self.funcName(self.func), str(round(self.param,4)))
С объектом генотипа пришлось немного повозиться, подбирая алгоритм скрещивания. Какой из них лучше, я так и не определился, оставил на волю псевдослучайности. Сам алгоритм был определен в методе умножения __mul__.
Объект Dnk
class Dnk:
gen = []
level = 0
def __init__(self, genlen=10):
super().__init__()
self.gen = [ Gen(1), Gen(1) ] + [ Gen() for i in range(genlen-2) ]
def copy(self, src):
self.gen = src.gen
def __mul__(self, other):
divider = 2
def sel():
v = random.random()*(self.level + other.level)
return v <=self.level
mode = random.randint(0,3)
minLen = min(len(self.gen), len(other.gen))
maxLen = max(len(self.gen), len(other.gen))
n = Dnk()
if mode == 0:
n.gen = [ self.gen[i] if sel() else other.gen[i] for i in range(minLen) ]
elif mode == 1:
n.gen = [ Gen() for i in range(minLen) ]
for g in n.gen:
g.param += round((random.random()-0.5)/divider,3)
elif mode == 2:
n.gen = [ self.gen[i-1] if i % 2 == 1 else other.gen[i] for i in range(minLen) ]
for g in n.gen:
g.param += round((random.random()-0.5)/divider,3)
else:
v = random.randint(0,1)
n.gen = [ self.gen[i] if i % 2 == v else other.gen[-1-i] for i in range(minLen) ]
for g in n.gen:
g.param += round((random.random()-0.5)/divider,3)
n.gen = n.gen + [ Gen() for i in range(minLen,maxLen) ]
return n
def calc(self, values):
res = []
mem = []
varr = values.copy()
i = 0
for g in self.gen:
try:
r = g.calc(varr, mem)
i = i + 1
except:
self.gen = self.gen[0:i]
#raise
break;
if not r is None:
res.append(r)
return res
def __str__(self):
return '(' + ', '.join([ str(g) for g in self.gen ]) + '):'+str(round(self.level,2))
Для обоих классов переопределен метод __str__, чтобы выводить их содержимое в консоль.
Функция просчета алгоритма чуть подробнее:
def calc(self, values):
res = []
mem = []
varr = values.copy()
i = 0
for g in self.gen:
try:
r = g.calc(varr, mem)
i = i + 1
except:
self.gen = self.gen[0:i]
#raise
break;
if not r is None:
res.append(r)
return res
Обратите внимание на закомментированный raise — первоначально у меня была идея, что генотип с алгоритмом, вылетающим по ошибке, не должен жить на этом свете и должен сразу отбраковаться. Но ошибок было слишком много, популяция вырождалась, и тогда я принял решение не уничтожать объект, а ампутировать его на этом гене. Так генотип становится короче, но остается рабочим, и его рабочие гены можно использовать.
Итак, есть генотип, есть словарь генов, есть функция скрещивания двух генотипов. Можно проверить:
>>> a = Dnk()
>>> b = Dnk()
>>> c = a * b
>>> print(a)
(push:4.061, push:1.79, dup:-4.32, mulMem:3.6, push:-3.752, addVal:2.4, delVal:-1.863, delMem:4.06, delVal:-3.692, addMem:0.48):0
>>> print(b)
(push:0.356, push:-4.8, pop:2.865, delVal:1.53, addMem:-2.853, mulVal:-1.6, const:-2.451, delVal:-2.53, divVal:4.424, delMem:-0.6):0
>>> print(c)
(push:4.061, divVal:4.424, dup:-4.32, const:-2.451, push:-3.752, addMem:-2.853, delVal:-1.863, pop:2.865, delVal:-3.692, push:0.356):0
>>> Теперь нужны функции размножения (отбор и скрещивание лучших) и мутации.
Функции скрещивания и размножения генотипов до необходимого количества я написал в трех вариантах. Но худшая половина погибает в любом случае.
# Скрещивание любой с любым из первой половины
def mixIts(its, needCount):
half = needCount // 2
its[half:needCount] = []
nIts = []
l = min(len(its), half)
ll = l // 2
for ii in range(half,needCount):
i0 = random.randint(0,l-1)
i1 = random.randint(0,l-1)
d0 = its[i0]
d1 = its[i1]
nd = d0 * d1
mutate(nd)
its.append(nd)
# Скрещивание родителя из первой четверти с родителем из второй четверти
def mixIts2(its, needCount):
half = needCount // 2
its[half:needCount] = []
nIts = []
l = min(len(its), half)
ll = l // 2
for ii in range(half,needCount):
i0 = random.randint(0,ll-1)
i1 = random.randint(ll,l-1)
d0 = its[i0]
d1 = its[i1]
nd = d0 * d1
mutate(nd)
its.append(nd)
# Скрещивание родителя из первой восьмой части с родителем из второй восьмой
def mixIts3(its, needCount):
half = needCount // 2
its[half:needCount] = []
nIts = []
l = min(len(its), half)
ll = l // 4
for ii in range(half,needCount):
i0 = random.randint(0,ll-1)
i1 = random.randint(ll,ll*2-1)
d0 = its[i0]
d1 = its[i1]
nd = d0 * d1
mutate(nd)
its.append(nd)
Функция мутации применяется к новому генотипу
def mutate(it):
# Три пары генов меняем местами
listMix = [
(random.randint(0,len(it.gen)-1), random.randint(0,len(it.gen)-1))
for i in range(3) ]
for i in listMix:
it.gen[i[0]], it.gen[i[1]] = (it.gen[i[1]], it.gen[i[0]])
# Три гена совсем новых,случайных
for i in [ random.randint(0,len(it.gen)-1) for i in range(3) ]:
it.gen[i] = Gen()
# У одного гена меняем параметр случайным образом
for i in [ random.randint(0,len(it.gen)-1) for i in range(1) ]:
it.gen[i].param = it.gen[i].param + (random.random()-0.5)*2
Как можно применить такой генетический алгоритм?
Например:
— выявлять закономерность среди входных данных, регрессионный анализ
— выработать алгоритм, восстанавливающий выпадения в сигнале и убирающий помехи — полезно для речевой связи
— разделять сигналы, пришедшие от разных источников по одному каналу — полезно для голосового управления, создания псевдостерео
Для этих задач нужен генотип, который примет на вход массив входных значений и выдаст массив выходных значений той же длины. Я пробовал совмещать задачи получения подходящих генотипов и достижения цели, оказалось слишком сложно. Проще было прогнать генетику с целью отбора генотипов для начальной популяции, чтобы эти генотипы вообще смогли обработать входной массив.
Для отбора генотипов написана функция, она генерит генотипы, прогоняет их по ГА, отбраковывает по результату и возвращает массив выживших. ГА прекращается раньше времени, если популяция выродилась.
# Длина массива входных и выходных данных
dataLen = 6
# Размер популяции
itCount = 100
# Начальная длина генотипа
genLen = 80
# Максимальное количество поколений
epochCount = 100
srcData = [ i+1 for i in range(dataLen) ]
def getIts(dest = 0):
its = [ Dnk(genLen) for i in range(itCount) ]
res = []
for epoch in range(epochCount):
nIts = []
maxAchiev = 0
for it in its:
try:
res = it.calc(srcData)
achiev = len(res)
if achiev == 0:
it = None
continue
maxAchiev = max(maxAchiev, achiev)
it.level = achiev
nIts.append(it)
except:
# print('Died',it[0],sys.exc_info()[1])
it = None
its = nIts
l = len(its)
if l<2:
print("Low it's count:",l)
break;
# отсортируем так, чтобы лучшие оказались первыми
its.sort(key = lambda it: -it.level)
if maxAchiev >= dataLen:
break;
mixIts(its, itCount)
for it in its[:]:
if it.level<dest:
its.remove(it)
return its
Функция оценки отклонения результата от искомого (не совсем фитнес-функция, т.к. чем больше отклонение, тем хуже генотип, но это учтем).
def diffData(resData, srcData):
# Если длина результата не верна, то не имеет смысла считать результат
if len(resData) != len(srcData):
return None
d = 0
for i in range(len(resData)):
d = d + abs((len(resData)*30 - i) * (resData[i] - srcData[i]))
return d
Ну и последний штрих — собственно ГА на отобранных генотипах.
# Размер популяции
bestCount = 30
# Максимальное количество поколений
globCount = 30000
# Ищем генотип, на котором отклонение будет меньше этой цифры
seekValue = 8000
its = []
while len(its)<bestCount:
its = its + getIts(len(destData))
print('Its len', len(its))
# Показать, с какого результата начинаем
printIts(its[0:1], srcData)
its[bestCount:len(its)]=[]
for glob in range(globCount):
minD = None
for it in its[:]:
resData = it.calc(srcData)
d = diffData(resData, destData)
# Если результат совсем плохой, то отбраковываем этот генотип.
if d is None:
its.remove(it)
continue
# Из значения отклонения получаем значение приспособленности генотипа
it.level = 100000 - d
minD = d if minD is None else min(d, minD)
its.sort(key = lambda it: -it.level)
if glob % 100 == 0 or glob == globCount - 1:
# Вывести текущий прогресс, выводим на каждый 100-й раз
print('glob', glob, ':', round(minD,3) if minD else 'None', len(its)) #, resData)
if minD < seekValue:
print('Break')
break
mixIts2(its, bestCount)
# Вывести лучшие три результата
printIts(its[0:3], srcData)
Результат
...
glob 2900 : 7067.129 18
glob 3000 : 4789.967 15
glob 3100 : 6791.239 17
glob 3200 : 6809.478 15
Break
16
0 (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, mulVal:4.7857, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399):97009.88 => [9.571, 24.952, 30.989, 35.638, 50.462, 65.698]
1 (const:24.7735, dup:-4.8988, dup:39.1318, dup:-4.3082, mulVal:24.952, mulVal:6.1096, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7128):96761.03 => [12.219, 24.952, 35.226, 39.875, 54.698, 59.007]
2 (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, delVal:3.4959, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399):96276.27 => [5.496, 24.952, 30.989, 35.638, 50.462, 65.698]
>>> Или, проще говоря, лучший результат ГА с целью destData = [10, 20, 30, 40, 50, 60] получился [9.571, 24.952, 30.989, 35.638, 50.462, 65.698]. Этого результата добивается генотип с алгоритмом (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, mulVal:4.7857, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399).
С одной стороны, алгоритм избыточен — он делает действия, ненужные для получения конечного результата. С другой — алгоритм ограничен, так как использует только два значения из входного потока из шести — понятно, что так получилось из-за ограниченных входных данных.
Что дальше?
Дальше можно развить идею:
— Прогонять полученный алгоритм на большом потоке данных, и чем дальше алгоритм «пройдет» по этому потоку с минимальным отклонением, тем он лучше, генотип получился более качественный. Полная аналогия с машинками.
— Включить полноценную Forth-машину и сделать генерацию алгоритма в текст Forth. Так можно создавать более сложные алгоритмы вычисления, с условными переходами и циклами.
— Анализировать и упрощать полученный алгоритм, чтобы в нем оставалось только самое необходимое для получения результата.
— Вместо элементарных операций в генах использовать более сложные. Например, такой операцией может быть дифференцирование. Или интегрирование. Или обучение нейронной сети. Хоть Алан Джей Перлис и говорил, что нужно не раздувать словарь, а накапливать идиомы, хороший словарь идиом не помешает.






