Ни в одной области электроники не скопилось столько мифов,
как в области Hi-Fi и Hi-End устройств для воспроизведения звука.
Ударим Рождественской Историей по одному из них!

Когда старый год уже проводили, Новый встретили сначала в узком семейном кругу, а затем с более дальними родственниками, когда закончились или пришли в негодность новогодние салаты и стало отпускать похмелье…
Те, кто не захотелили не смог встречать Новый Год в Дальнем Зарубежье, начинают ощущать на себе зов персонального компьютера.
Именно для них и предназначена моя рождественская история, об основах ресемплинга — технологии, позволившей значительно улучшить качество воспроизведения дисков формата Аудио CD в начале тысячелетия. Именно тогда для воспроизведения 16 битных записей начали применять 18 и даже 20 битные цифро-аналоговые преобразователи. С первого взгляда это выглядело как маркетинговая уловка производителей, направленная на извлечение дополнительной порции денег из кошельков доверчивых аудиофилов, но в этот раз сторонники теории заговоров могут курить в сторонке. На самом деле это было удачной попыткой улучшить качество воспроизведения и снизить цену дорогостоящей профессиональной аппаратуры. История старая, но поучительная, во многом актуальная и по сей день.
Цифро-аналоговый преобразователь digital-to-analog DAC является сердцем любой аудиовопроизводящей системы, использующей в качестве источника компакт диски. На него возложена сложная и деликатная задача раскодирования последовательности 16-битных чисел и преобразования её в формат, воспринимаемый человеческим ухом.

В далёком 1983 году появился первый культовый CD проигрыватель Magnavox со сдвоенным 14 битным конвертором, но уже к началу века многие системы высококачественного воспроизведения CD дисков имели 18, а то и 20 битные преобразователи. Почему?
Концепция цифро-аналоговых преобразований покоится на двух китах: частоте дискретизации sampling и разрядности quantization.
Для воспроизведения звука в PCM формате мы должны через равные промежутки времени преобразовывать цифровые значения в соответствующие им аналоговые величины напряжения или тока. Частота этих преобразований и является частотой дискретизации. Согласно теореме Найквиста, таким образом возможно воспроизводить сигналы с частотой не выше половины частоты дискретизации. Наиболее распространённые форматы, которые способны воспроизводить сигналы с частотой воспринимаемой человеческим ухомобщепринята цифра 20 кГц, имеют частоты дискретизации в 44.1 и 48 КГц.

Первый до сих пор широко используется в звуковых компакт дисках (CDDA, англ. Compact Disc Digital Audio, также называемый англ. Audio CD и Red Book), а второй зародился в ряде стандартов для профессиональной звукозаписывающей аппаратуры.
Давайте вообразим себе что при записи звуковой сигнал попадает на идеальный аналогово-цифровой преобразователь. Он не имеет собственных шумов и искажений и преобразует мгновенное значение поступающего на него сигнала в цифровое с заданной разрядностью, ну например в 16 бит, как это принято в формате Audio CD. В таком случае, теоретически достижимый динамический диапазон сигнала (соотношение между оцифрованными сигналами с самым большим и маленьким уровнями) будет составлять 98.1 dB. Для вычисления этой величины часто используют приближённую формулу, согласно которой каждый лишний бит добавляет 6 децибел к теоретически достижимому динамическому диапазону. Для 16 битного сигнала мы получим:
6dB/bit*16bits=96dB.
Реальный музыкальный сигнал чаще всего состоит не из чистого тона, а из смеси большого количества быстро меняющих свою частоту и амплитуду гармоник. Для гармоник, имеющих амплитуду менее одного разряда АЦП, невозможно восстановить корреляцию с исходным сигналом и они в результате операции кодирования-декодирования превращаются в белый шум. Кроме этого, шумы генерируются быстро изменяющимися сигналами с большой амплитудой, которых много скажем в поп музыке.
Со времён начала использования цифровых технологий в звукозаписи ведётся постоянная гонка за увеличение их производительности и уменьшение стоимости. Первые CD проигрыватели имели единственный параллельный DAC и две входные цепи, которые поочерёдно подавали на него сигналы то правого, то левого каналов. Мгновенные уровни аналоговых сигналов на выходе DAC фиксировались с помощью специальных цепей на время между двумя считываниями и попеременно поступали на отдельные усилители правого и левого каналов. Это порождало дополнительные искажения, величина которых зависела от разности мгновенных звуковых уровней каналов. Под напором критики ауидофилов производители вынуждены были перейти на схему с отдельными DAC для каждого из каналов.
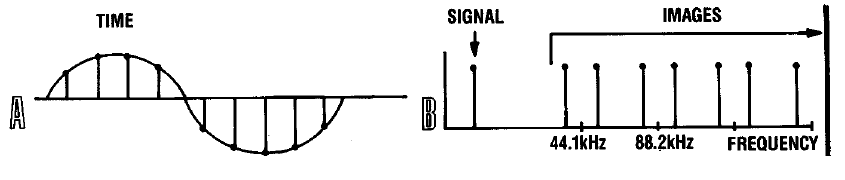
 На выходе DAC присутствует ступенчатый сигнал, который не слишком похож на плавный исходный, в нём существуют неприятные на слух искажения. Давайте для упрощения представим что на вход была подана единственная гармоника с частотой 1 КГц. Операция восстановления оцифрованного сигнала приводит фактически к возникновению интермодуляционных искажений между исходным сигналом и частотой дискретизации — в нашем случае 44.1 КГц. (Механизм возникновения интермодуляционных искажений и ликбез по гармоникам при необходимости ищите в моей прошлой статье).
На выходе DAC присутствует ступенчатый сигнал, который не слишком похож на плавный исходный, в нём существуют неприятные на слух искажения. Давайте для упрощения представим что на вход была подана единственная гармоника с частотой 1 КГц. Операция восстановления оцифрованного сигнала приводит фактически к возникновению интермодуляционных искажений между исходным сигналом и частотой дискретизации — в нашем случае 44.1 КГц. (Механизм возникновения интермодуляционных искажений и ликбез по гармоникам при необходимости ищите в моей прошлой статье).
Несмотря на то, что паразитные гармоники лежат за пределами человеческого уха, они оказывают неблагоприятное воздействие на усилительный тракт и от них лучше избавиться.
В ранних моделях аппаратуры для воспроизведения цифрового контента для этого использовались фильтры, которые имели плоскую характеристику до частоты в 20 кГц, а далее резкое ослабление уровня на 80дБ и более. В английской терминологии такие фильтры называют brick-wall, на русском иногда именуют по аналогии “кирпичной стеной”. Проблема заключалась в том, что аналоговые ФНЧ высокого порядка очень чувствительны к точности значений пассивных компонентов, из которых они состоят. Ещё больше осложняют ситуацию требуемые номиналывыбивающиеся за пределы стандартного ряда и особые требования к качеству этих компонентов, которое необходимо для достижения минимального вклада в искажение сигнала. В результате, стоимость данных фильтров получалась запредельной, но самое печальное — они не смогли удовлетворить запросы аудиофилов, поскольку данные фильтры имели большие фазовые искажения, особенно на краях воспроизводимого диапазона. Поэтому звучание ранних версий CD проигрывателей несмотря на высокую стоимость аудиофилы характеризовали как “песочное” (gritty).
Серьёзным шагом в направлении улучшения качества звукаа главное его доступности было внедрение технологии передискретизации сигнала, которой собственно и посвящена данная статья.
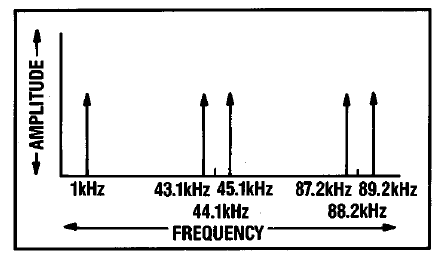
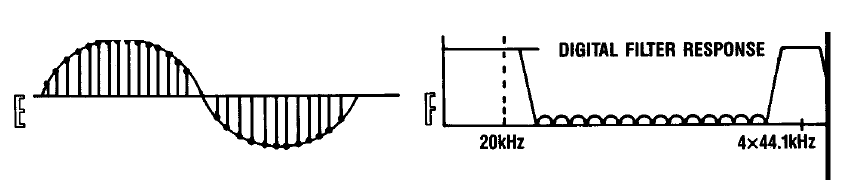
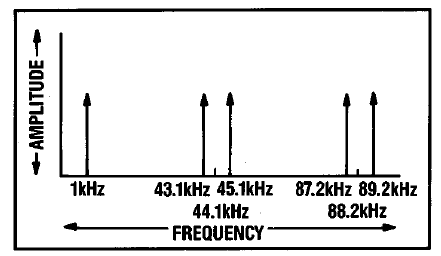
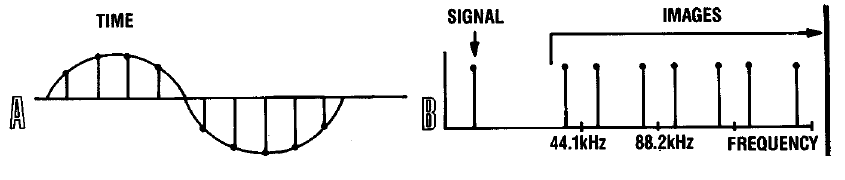
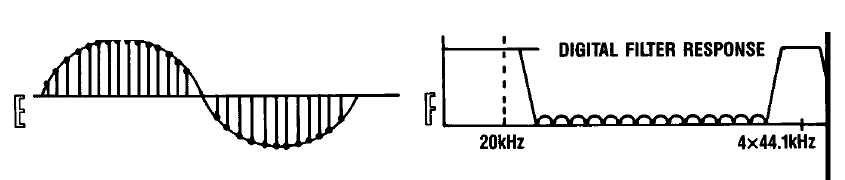
Для того, чтобы пояснить её сущность давайте представим процесс восстановления сигнала с так любимой ГОСТами частотой 1 КГц. На рисунке A представлен ряд сэмплов составляющих сигнал, которые появляются на выходе DAC, а правее спектральные составляющие второго и третьего порядков, содержащиеся в сигнале на выходе DAC. Можно заметить, что сигнал является ни чем иным, как продуктом интермодуляционных искажений между исходным тоном с частотой 1 КГц и частой оцифровки 44.1 КГц.
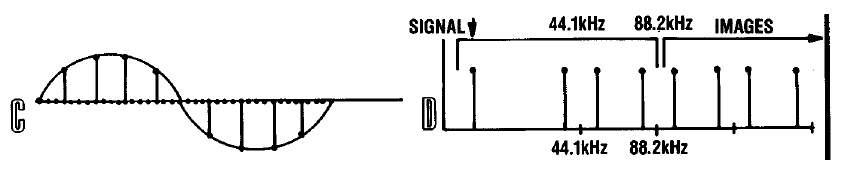
Увеличим частоту дискретизации сигнала в четыре раза путём элементарной операции — добавления лишних трёх сэмплов между двумя соседними, каждый из которых имеет нулевые значения, как показано на рисунке C. Одновременно с этим добавим два младших разряда в каждый сэмпл, также заполнив их нулями. Теперь мы получили 18 битные значения сэмплов. В результате этой операции спектр сигнала фактически не изменился, но на самом деле произошло фундаментальное изменение. Гармоники второго порядка, вызванные частотой дискретизации стали частью спектра основного сигнала. Производные же гармоники переместились выше частоты 44.1 кГц. Это показано на рисунке D.
В области же спектра основного сигнала с успехом можно применить цифровую фильтрацию, что мы и сделаем, использовав цифровой фильтр высокого порядка, с АЧХ показанный на рисунке F. Физически мы получаем дополнительные промежуточные точки между имеющимися сэмплами сигнала, которые сглаживают переходы между двумя значениями за счёт появления дополнительных двух разрядов в представлении амплитуды.
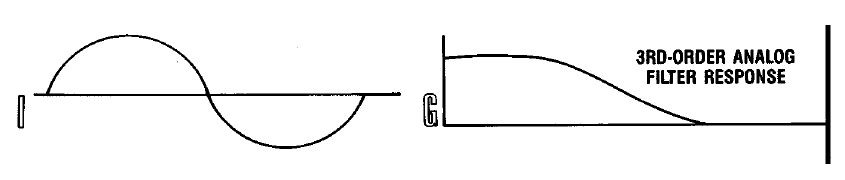
Теперь, когда всю тяжёлую и грязную работу выполнил цифровой фильтр мы подаём результирующий сигнал с частотой дискретизации в 44.1*4 =176.4 КГц, на DAC.
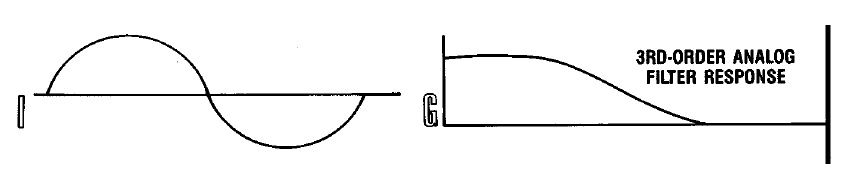
Осталось добавить вишенку на наш тортик — пропустить сигнал через простейший аналоговый фильтр третьего порядка, который отлично справится с подавлением гармоник в заданном диапазоне и не внесёт при этом заметных фазовых искажений.
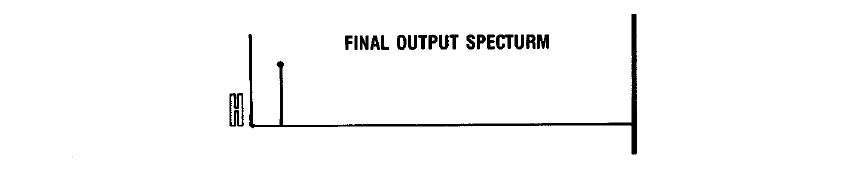
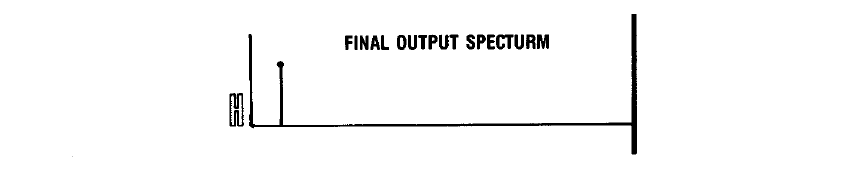
Результат — спектр полученного сигнала стал гораздо ближе к исходному, паразитные составляющие в нём сильно ослаблены, а фазовые искажения сведены к минимуму благодаря возможностям цифровой фильтрации.
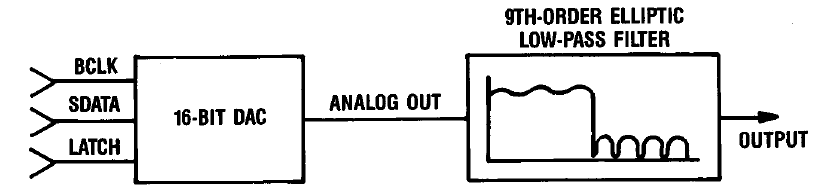
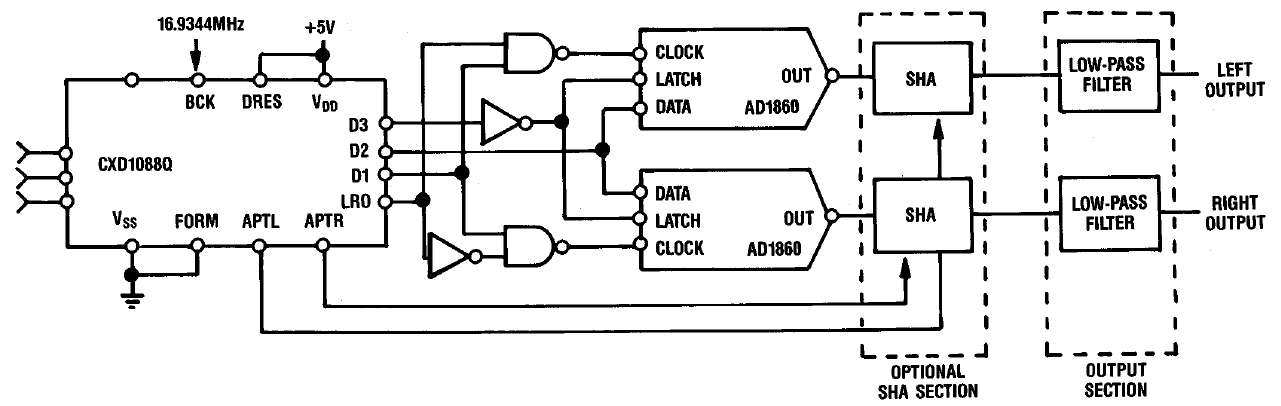
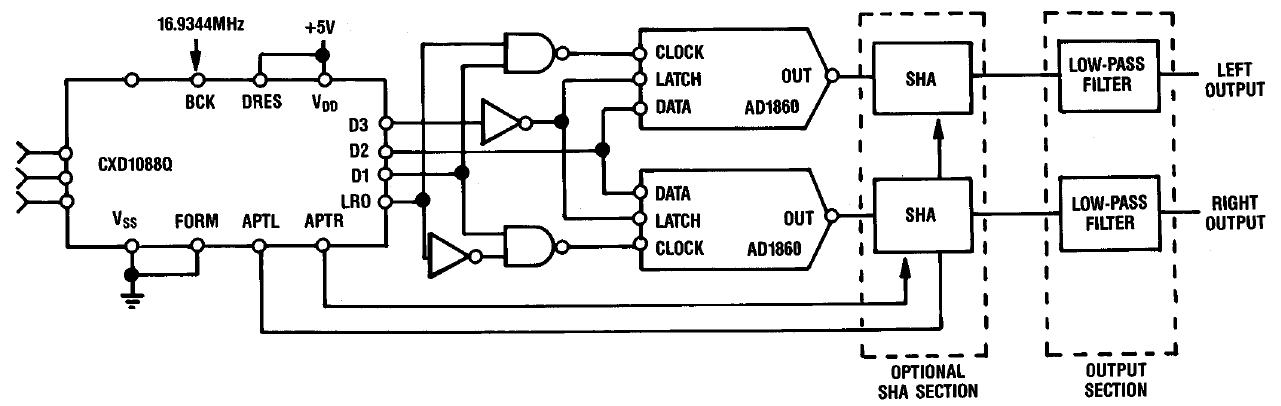
На рисунке представлена аппаратная реализация описанного выше решения. Операции передискретизации и цифровой фильтрации выполняет микросхема CXD1088Q производства фирмы SONY — одним из прародителей формата Audio CD. Несложная логическая схема поочерёдно запускает преобразование двух отдельных 18 битных DAC AD1860.
Производители профессиональной аппаратуры и CD проигрывателей в сегменте Hi Fi смогли улучшить качество звука и значительно увеличить повторяемость параметров своих изделий в процессе производства.
Любители качественного звука получили проигрыватели дисков с улучшенными параметрами за разумную цену.
Законченные аудиофилы теперь могут ворчать о том, какой крутой звук был у старых аппаратов с аналоговыми фильтрамипока всё не испортила цифра и охотиться за винтажной техникой.
Ну а избранные производители хайэнда могут создавать единичные экземпляры устройств, тщательно подбирая компоненты аналогового фильтра с характерным названием “кирпичная стена”, получая при этом аппараты с индивидуальным звучанием обусловленным в основном вносимыми фильтрами фазовымии не только искажениями и задирать их ценник до небес.
При подготовке публикации были использованы материалы статьи DAC ICs: How Many Bits is Enought? под авторством Robert Adams
как в области Hi-Fi и Hi-End устройств для воспроизведения звука.
Ударим Рождественской Историей по одному из них!

Когда старый год уже проводили, Новый встретили сначала в узком семейном кругу, а затем с более дальними родственниками, когда закончились или пришли в негодность новогодние салаты и стало отпускать похмелье…
Те, кто не захотел
Именно для них и предназначена моя рождественская история, об основах ресемплинга — технологии, позволившей значительно улучшить качество воспроизведения дисков формата Аудио CD в начале тысячелетия. Именно тогда для воспроизведения 16 битных записей начали применять 18 и даже 20 битные цифро-аналоговые преобразователи. С первого взгляда это выглядело как маркетинговая уловка производителей, направленная на извлечение дополнительной порции денег из кошельков доверчивых аудиофилов, но в этот раз сторонники теории заговоров могут курить в сторонке. На самом деле это было удачной попыткой улучшить качество воспроизведения и снизить цену дорогостоящей профессиональной аппаратуры. История старая, но поучительная, во многом актуальная и по сей день.
Цифро-аналоговый преобразователь digital-to-analog DAC является сердцем любой аудиовопроизводящей системы, использующей в качестве источника компакт диски. На него возложена сложная и деликатная задача раскодирования последовательности 16-битных чисел и преобразования её в формат, воспринимаемый человеческим ухом.

В далёком 1983 году появился первый культовый CD проигрыватель Magnavox со сдвоенным 14 битным конвертором, но уже к началу века многие системы высококачественного воспроизведения CD дисков имели 18, а то и 20 битные преобразователи. Почему?
Немного теории, почти без формул
Концепция цифро-аналоговых преобразований покоится на двух китах: частоте дискретизации sampling и разрядности quantization.
Для воспроизведения звука в PCM формате мы должны через равные промежутки времени преобразовывать цифровые значения в соответствующие им аналоговые величины напряжения или тока. Частота этих преобразований и является частотой дискретизации. Согласно теореме Найквиста, таким образом возможно воспроизводить сигналы с частотой не выше половины частоты дискретизации. Наиболее распространённые форматы, которые способны воспроизводить сигналы с частотой воспринимаемой человеческим ухом

Первый до сих пор широко используется в звуковых компакт дисках (CDDA, англ. Compact Disc Digital Audio, также называемый англ. Audio CD и Red Book), а второй зародился в ряде стандартов для профессиональной звукозаписывающей аппаратуры.
Давайте вообразим себе что при записи звуковой сигнал попадает на идеальный аналогово-цифровой преобразователь. Он не имеет собственных шумов и искажений и преобразует мгновенное значение поступающего на него сигнала в цифровое с заданной разрядностью, ну например в 16 бит, как это принято в формате Audio CD. В таком случае, теоретически достижимый динамический диапазон сигнала (соотношение между оцифрованными сигналами с самым большим и маленьким уровнями) будет составлять 98.1 dB. Для вычисления этой величины часто используют приближённую формулу, согласно которой каждый лишний бит добавляет 6 децибел к теоретически достижимому динамическому диапазону. Для 16 битного сигнала мы получим:
6dB/bit*16bits=96dB.
Реальный музыкальный сигнал чаще всего состоит не из чистого тона, а из смеси большого количества быстро меняющих свою частоту и амплитуду гармоник. Для гармоник, имеющих амплитуду менее одного разряда АЦП, невозможно восстановить корреляцию с исходным сигналом и они в результате операции кодирования-декодирования превращаются в белый шум. Кроме этого, шумы генерируются быстро изменяющимися сигналами с большой амплитудой, которых много скажем в поп музыке.
От идеальных приближений к реальной жизни. Проблемы первых CD проигрывателей
Со времён начала использования цифровых технологий в звукозаписи ведётся постоянная гонка за увеличение их производительности и уменьшение стоимости. Первые CD проигрыватели имели единственный параллельный DAC и две входные цепи, которые поочерёдно подавали на него сигналы то правого, то левого каналов. Мгновенные уровни аналоговых сигналов на выходе DAC фиксировались с помощью специальных цепей на время между двумя считываниями и попеременно поступали на отдельные усилители правого и левого каналов. Это порождало дополнительные искажения, величина которых зависела от разности мгновенных звуковых уровней каналов. Под напором критики ауидофилов производители вынуждены были перейти на схему с отдельными DAC для каждого из каналов.
 На выходе DAC присутствует ступенчатый сигнал, который не слишком похож на плавный исходный, в нём существуют неприятные на слух искажения. Давайте для упрощения представим что на вход была подана единственная гармоника с частотой 1 КГц. Операция восстановления оцифрованного сигнала приводит фактически к возникновению интермодуляционных искажений между исходным сигналом и частотой дискретизации — в нашем случае 44.1 КГц. (Механизм возникновения интермодуляционных искажений и ликбез по гармоникам при необходимости ищите в моей прошлой статье).
На выходе DAC присутствует ступенчатый сигнал, который не слишком похож на плавный исходный, в нём существуют неприятные на слух искажения. Давайте для упрощения представим что на вход была подана единственная гармоника с частотой 1 КГц. Операция восстановления оцифрованного сигнала приводит фактически к возникновению интермодуляционных искажений между исходным сигналом и частотой дискретизации — в нашем случае 44.1 КГц. (Механизм возникновения интермодуляционных искажений и ликбез по гармоникам при необходимости ищите в моей прошлой статье).Несмотря на то, что паразитные гармоники лежат за пределами человеческого уха, они оказывают неблагоприятное воздействие на усилительный тракт и от них лучше избавиться.
В ранних моделях аппаратуры для воспроизведения цифрового контента для этого использовались фильтры, которые имели плоскую характеристику до частоты в 20 кГц, а далее резкое ослабление уровня на 80дБ и более. В английской терминологии такие фильтры называют brick-wall, на русском иногда именуют по аналогии “кирпичной стеной”. Проблема заключалась в том, что аналоговые ФНЧ высокого порядка очень чувствительны к точности значений пассивных компонентов, из которых они состоят. Ещё больше осложняют ситуацию требуемые номиналы
Цифровые фильтры спешат на помощь. Oversampling на пальцах
Серьёзным шагом в направлении улучшения качества звука
Для того, чтобы пояснить её сущность давайте представим процесс восстановления сигнала с так любимой ГОСТами частотой 1 КГц. На рисунке A представлен ряд сэмплов составляющих сигнал, которые появляются на выходе DAC, а правее спектральные составляющие второго и третьего порядков, содержащиеся в сигнале на выходе DAC. Можно заметить, что сигнал является ни чем иным, как продуктом интермодуляционных искажений между исходным тоном с частотой 1 КГц и частой оцифровки 44.1 КГц.
Увеличим частоту дискретизации сигнала в четыре раза путём элементарной операции — добавления лишних трёх сэмплов между двумя соседними, каждый из которых имеет нулевые значения, как показано на рисунке C. Одновременно с этим добавим два младших разряда в каждый сэмпл, также заполнив их нулями. Теперь мы получили 18 битные значения сэмплов. В результате этой операции спектр сигнала фактически не изменился, но на самом деле произошло фундаментальное изменение. Гармоники второго порядка, вызванные частотой дискретизации стали частью спектра основного сигнала. Производные же гармоники переместились выше частоты 44.1 кГц. Это показано на рисунке D.
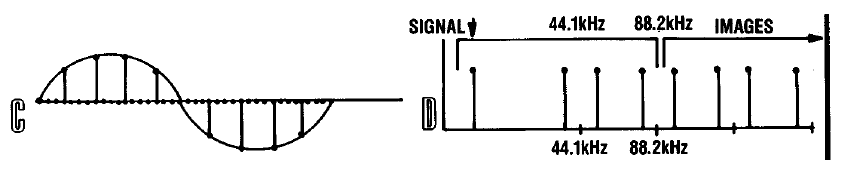
В области же спектра основного сигнала с успехом можно применить цифровую фильтрацию, что мы и сделаем, использовав цифровой фильтр высокого порядка, с АЧХ показанный на рисунке F. Физически мы получаем дополнительные промежуточные точки между имеющимися сэмплами сигнала, которые сглаживают переходы между двумя значениями за счёт появления дополнительных двух разрядов в представлении амплитуды.
Теперь, когда всю тяжёлую и грязную работу выполнил цифровой фильтр мы подаём результирующий сигнал с частотой дискретизации в 44.1*4 =176.4 КГц, на DAC.
Осталось добавить вишенку на наш тортик — пропустить сигнал через простейший аналоговый фильтр третьего порядка, который отлично справится с подавлением гармоник в заданном диапазоне и не внесёт при этом заметных фазовых искажений.
Результат — спектр полученного сигнала стал гораздо ближе к исходному, паразитные составляющие в нём сильно ослаблены, а фазовые искажения сведены к минимуму благодаря возможностям цифровой фильтрации.
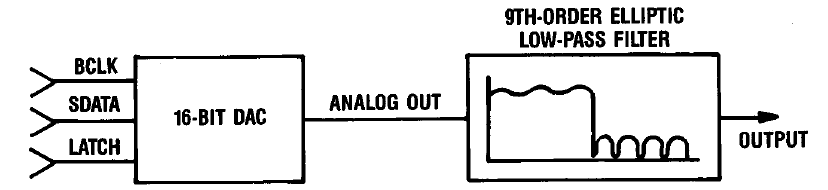
Аппаратная реализация
На рисунке представлена аппаратная реализация описанного выше решения. Операции передискретизации и цифровой фильтрации выполняет микросхема CXD1088Q производства фирмы SONY — одним из прародителей формата Audio CD. Несложная логическая схема поочерёдно запускает преобразование двух отдельных 18 битных DAC AD1860.
Какие же преимущества мы получили в результате наших цифровых фокусов?
- Снижение интермодуляционных искажений
- Низкие фазовые искажения, вносимые фильтром
- Отличное подавление высших гармоник, возникающий в процессе цифро-аналогового преобразования, которые могут служить источником возникновения интермодуляционных искажений в усилительном тракте
- Применение ЦАП с большей разрядностью позволяет уменьшить нелинейности преобразования и коэффициент гармонических искажений в силу того, что они имеют лучшие параметры
- Благодаря использованию специализированных чипов вместо сложных аналоговых фильтров, снизилась цена реализации, размеры и потребляемая мощность аппаратного решения.
Каждому яблоку место упасть, каждому вору возможность украсть…
Как любая хорошая рождественская история, эта имеет хэппиенд. От внедрения новой технологии кажется выиграли все:
Производители профессиональной аппаратуры и CD проигрывателей в сегменте Hi Fi смогли улучшить качество звука и значительно увеличить повторяемость параметров своих изделий в процессе производства.
Любители качественного звука получили проигрыватели дисков с улучшенными параметрами за разумную цену.
Законченные аудиофилы теперь могут ворчать о том, какой крутой звук был у старых аппаратов с аналоговыми фильтрами
Ну а избранные производители хайэнда могут создавать единичные экземпляры устройств, тщательно подбирая компоненты аналогового фильтра с характерным названием “кирпичная стена”, получая при этом аппараты с индивидуальным звучанием обусловленным в основном вносимыми фильтрами фазовыми
Более подробное сравнение работы аналоговых и цифровых фильтров и ответы на характерные вопросы читайте в следующей статье
.При подготовке публикации были использованы материалы статьи DAC ICs: How Many Bits is Enought? под авторством Robert Adams






