Ода Джулии
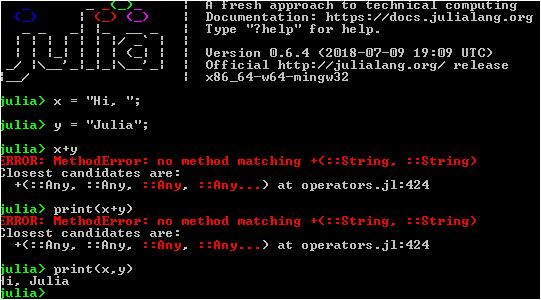
Очень трудно передать весь восторг, который сопутствовал запуску первых программ и исправлению первых ошибок с использованием этого языка. Прост и красив как Python, немножко похож на Fortran, удобная работа с массивами и графиками, а также возможность осуществлять лютую оптимизацию и распараллеливание даже для таких чайников, как я мои одногруппники. Можно работать на разных уровнях абстракции: от высокоуровневого программирования с динамической типизацией можно спуститься до ассемблерных команд, то есть, тут вам и питонская общедоступность и скорость выполнения фортрановских считалок. Не могу отделаться от ощущения, что Mathcad, Scilab и даже, прости Господи, C++ начинают в моем сердце уходить на второй план.
Узнал про язык случайно наткнувшись на хабровскую публикацию, и, как полагается впечатлительному студенту, стал искать руководства, да желательно на русском. Так как язык в течение шести лет постоянно развивался, и без того скудные источники информации устаревали, и азарт начал убывать. Но вот с началом нового лабораторного курса по моделированию физических явлений со свободным выбором языка программирования, таки появилась мотивация начать знакомство с Джулией. К тому же, в августе язык "допекли 1.0".
Нижепредставленный материал планировался как введение в язык, на котором в дальнейшем были написаны все лабораторные и собрана методичка.
Julia — высокоуровневый, высокопроизводительный язык программирования с динамической типизацией для математических вычислений. Синтаксис похож на матлабово семейство, язык написан на Си, С++ и Scheme, есть возможность вызова Сишных библиотек
Установка
На официальном сайте можно найти новости, видеоуроки и загрузить дистрибутив. После установки можно приступать к работе, но всё будет происходить в режиме интерпритатора.
На сайте https://juliacomputing.com доступны продукты, основой для которых послужил этот язык:
- JuliaDB — для работы с аналитикой баз данных и аналитикой временных рядов, основанными на богатой экосистеме Джулии, а также располагающими встроенным параллелизмом и масштабируемостью.
- JuliaBOX — Запустите Julia без установки из вашего браузера в ноутбуках Jupyter. Популярна в университетах и среди начинающих пользователей. Для полноценной работы нужно оформлять платную подписку. В бесплатном же режиме некоторые опции будут ограничены, и для доступа к вычислительным ядрам нужно ждать в очереди
- JuliaRun — Запускайте приложения Julia в публичном или частном облаке. Масштабируемое развертывание в производстве для анализа в реальном времени и для крупномасштабных параллельных симуляций.
- JuliaFin — Для работы в сфере финансов. Включает в себя все инструменты, необходимые для бэктестинга и торговли: Excel, Bloomberg, моделирование контрактов и JuliaDB.
- JuliaPro — Бесплатная версия для ученых и исследователей данных. Установите в Windows, Mac или Linux. Доступна расширенная коммерческая лицензия.
Выбираем последний вариант. На момент написания руководства доступна версия 0.6.4.1. После регистрации будет доступно бесплатное скачивание. Пользователи Windows 7/Windows Server 2012 также должны установить:
- TLS easy_fix Чтоб узнать детали смотрите Discourse thread.
- Windows Management Framework 3.0 or later.
Скачав фиксер, лучше обеспечьте ограничение на выход в интернет, а уж потом обновляйте, не то все узнают какая у вас недействительная копия Windows. Это обновление нужно, чтоб предотвратить проблемы с системой контроля версий git, иначе не будет возможности докачивать дополнительные пакеты, а без них будет тяжко.
Ну вот, всё наконец-таки установилось, теперь в нашем распоряжении:
- JuliaPRO Command Prompt — все Юлины умения прямо из интерпретатора.
- Juno — красивая IDE с окошком для графиков и рабочим пространством, где можно смотреть содержимое всех объектов
- Jupyter — запускает вычислительное ядро в консоли, а выполнять код можно прямо в браузере. (Помимо Джулии присутствует еще и Питон)
Посмотрим, что умеет этот калькулятор… Поддержка Юникода — можно использовать кириллицу, иероглифы и назвать pi греческой буквой. А еще можно явно не указывать умножение между числом и переменной (именно в таком порядке и без пробела):
x = 5+8
2x - 3x + 2x^2
Out: 325Все нужные знаки тоже на месте: +=, *=, >>= и т.д. (Знак ">>" (битовый сдвиг вправо). Знаки сравнения: >, >=, <, <=, ==, !=. Неравенства можно объединять в цепочки:
y = 5
y += 2
4 <= y < 8
Out: trueКомплексные числа в наличии:
(2-1im)*(4+3im)
Out: 11 + 2imИ функции для работы с ними:
- real(z) — действительная часть,
- imag(z) — мнимая часть,
- conj(z) — комплексно сопряжённое число,
- abs(z) — модуль,
- abs2(z) — квадрат модуля,
- angle(z) — аргумент комплексного числа.
Можно пользоваться рациональными числами используя "//" и соответствующими функциями:
- num(x) — числитель,
- den(x) — знаменатель,
- float(x) — преобразует к десятичной дроби
x = 4//6+5//7
Out: 29//21
float(x)
Out: 1.380952380952381В Julia есть возможность управлять внутренним представлением данных:
- typeof(obj) — тип объекта
- typemax(obj) — максимальное число этого типа
- typemin(obj) — мимимальное
- eps() — машинный ноль
- BigInt — большое целое
- BigFloat — большое с плавающей точкой
q = 3
typemax(q)
Out: 9223372036854775807
typeof(q)
Out: Int64
BigFloat(2.3^45/6)
Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15Функции
Комплект особоупотребительных функций
- abs(x) — модуль числа,
- abs2(x) — квадрат модуля,
- sqrt(x) — квадратный корень,
- cbrt(x) — кубический корень,
- exp(x) — экспонента числа,
- log(x) — натуральный логарифм,
- log10(x) — десятичный логарифм,
- log(b,x) — логарифм x по основанию b.
А также тригонометрические, гиперболические, Эйри, Бессель и еще много всяких других.
Пользовательские функции:
function имя(аргументы)
#тело функции
endФункция возвращает результат последнего выражения (Икнул пользователь Mathcad).
function cube(x)
x^3
end
cube(4)
Out: 64Ну, или укажем явно:
function myabs(x)
if x>=0
return x
else
return -x
end
end
myabs(-12)
Out: 12Возвращаемые значения можно собрать в кортеж:
function cubeandsquare(x)
x^3,x^2
end
a,b = cubeandsquare(3)
print("a = $a, b = $b")
Out: a = 27, b = 9Функции могут принимать кортежи, значения по-умолчанию, ключевые слова. Если после имени функции отсутствуют скобки, оно рассматривается как переменная и может быть присвоено другой переменной или передано в функцию как параметр. Еще Julia поддерживает и функциональный стиль написания программ (привет Lisp`у)
function mysin(t;A=1,ω=1,φ=0) # поддержка Юникода - можно использовать греческие символы
A*sin(ω*t + φ)
end
x1 = mysin(pi) # синус Пи = 0
x2 = mysin(pi*0.5,A = 2) # увеличиваем амплитуду в два раза
x3 = mysin(pi*0.5,ω = 0.5) # уменьшаем в два раза частоту
print("x1 = $x1, x2 = $x2, x3 = $x3")
Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475Массивы
Я как пользователь Scilab даже не заметил подмены: можно задать массив с помощью функции:
- Array{T}(undef, dims...) — Массив типа Т и размерности dims
- zeros(T, dims...) — Массив нулей
- ones(T, dims...)- или единиц
Индексация начинается с единицы, вместо$—end, а также определены все необходимые операции для матриц (для того чтоб осуществить, скажем, поэлементное сложение или умножение, перед оператором нужно ставить точку).

(Теперь понятно как картинки вставлять, но ладно уж...)
Базовые функции:
- det(A) — вычислить определитель
- A' — транспонировать матрицу
- inv(A) — инвертировать матрицу
- length(A) — число элементов
- ndims(A) — число размерностей
- size(A) — кортеж размерностей
- size(A, n) — размерность в заданном направлении
- copy(A) — создание копии массива
- linspace(начало, конец, шаг) или
linspace(начало: шаг: конец) — создание одномерного массива
A = [1 2 3; 6 5 4; 7 8 9]
Out: 3x3 Array{Int64,2}:
1 2 3
6 5 4
7 8 9
A[2,1]
Out: 6
A[end]
Out: 9
size(A)
Out: (3, 3)Можно выделять части массива, задавая диапазон индексов вдоль размерности знаком ": ".
m1 = rand(3,2)
m2 = reshape(1:2:11, 3,2)
Out: 3x2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}:
1 7
3 9
5 11
m3 = [m1 m2] # объединение строк (вдоль первой размерности)
Out: 3x4 Array{Float64,2}:
0.325649 0.701038 1.0 7.0
0.513579 0.620215 3.0 9.0
0.815242 0.805307 5.0 11.0
m5 = [m1; m2] # объединение столбцов (вдоль второй размерности)
Out: 6x2 Array{Float64,2}:
0.325649 0.701038
0.513579 0.620215
0.815242 0.805307
1.0 7.0
3.0 9.0
5.0 11.0
m3[:, 2:4]
Out: 3x3 Array{Float64,2}:
0.701038 1.0 7.0
0.620215 3.0 9.0
0.805307 5.0 11.0Здесь использовались rand(), возвращающая массив случайных чисел заданной размерности, и reshape(), изменяющая размерность массива на указанную.
for a in A
# действия над a из массива A
end или
for i in eachindex(A)
# действия с учётом индекса i
end или
for i = 1 : size(A,n)
# n - вдоль какой размерности бежит индекс (хм.. можно упростить трехмерное ВУ)
# действия с учётом индекса i
end Графики
Для использования графики нужно докачивать с репозитория пакет на выбор:
- Pkg.add("Plots")
- Pkg.add("PyPlot")
- Pkg.add("Gadfly")
- Pkg.add("Winston")
Из них наиболее популярен питоновский PyPlot. Модули подключаются командой using, например:
using PyPlotОднако, давайте попробуем Gaston использующий Gnuplot (качается отдельно).
Загружается Gaston.jl командой
Pkg.add("Gaston")И сразу к делу:
using Gaston
t = 0:0.01:1
plot(t, sin.(2π*5*t))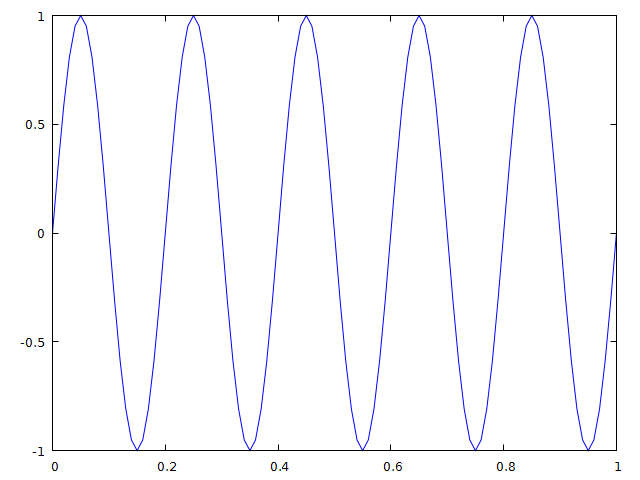
plot(t,sin.(2π*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue",
yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-")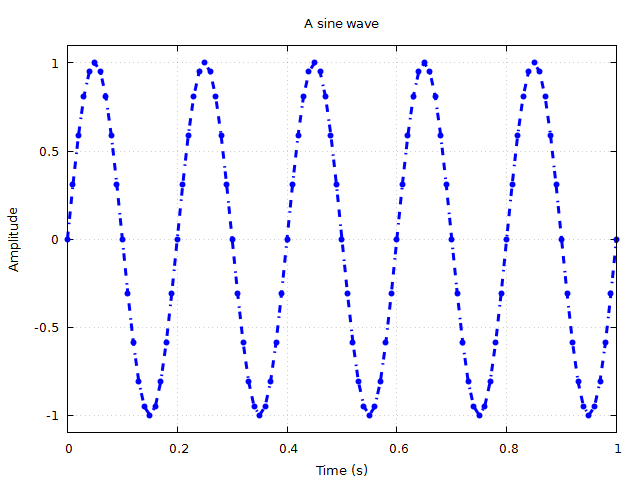
plot!(t,cos.(2π*5*t),color="red",linewidth=2) # добавляем во фрейм еще один график
x = y = -15:0.33:15
surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d")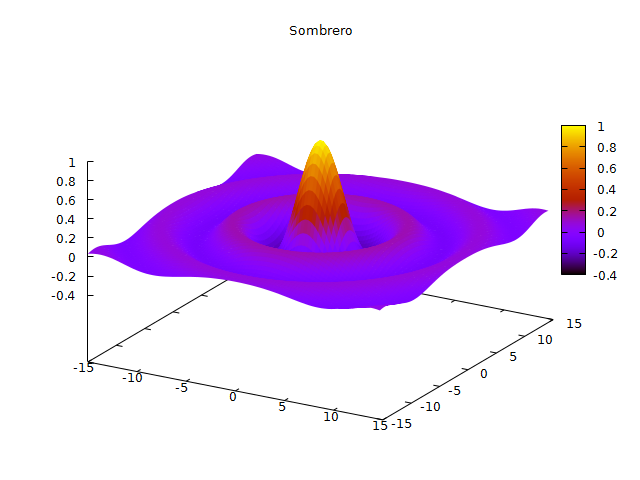
x = y = -15:0.33:15
surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y),
title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20")
R = [ x+y for x=0:5:120, y=0:5:120]
G = [ x+y for x=0:5:120, y=120:-5:0]
B = [ x+y for x=120:-5:0, y=0:5:120]
Z = zeros(25,25,3)
Z[:,:,1] = R
Z[:,:,2] = G
Z[:,:,3] = B
imagesc(Z,title="RGB Image",clim=[10 200])
histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]")
y = 1:40
err = Gaston.ErrorCoords(rand(40))
plot(y,err=err,title="Example of error bars",plotstyle="errorbars")
Можно создавать несколько графических окон (не работает в Jupyter) используя команду h = figure() (Просто вставить между plot'ами). Чтобы сохранить график в виде файла изображения, используйте команды
set_filename("имя.png") # если не указать, выведется на экран
printfigure("png") # сохранить в файл, доступно PNG, PDF, SVG и GIF
Больше информации по пакету Gaston
Заключение
Есть еще много графических пакетов на любой вкус и покрывающих почти все потребности. Так-же вовсю развиваются вспомогательные пакеты. Тут вам и квантовые вычисления, и биоинформатика, и машинное обучение, и множество более насущных проблем вроде дифуров и производных.
В общем, Джулия красива, умна и очень перспективна, и крайне непозволительно оставлять её без должного внимания.






