Комментарии 21
Статья интересная — но, вот, мне кажется, пояснений немножечко не хватает. Вы пишете с расчетом на читателя, который прекрасно разбирается в оконных функциях, а наверно, стоило бы немного пояснить подробнее, зачем они нужны, для тех, кто не занимается ежедневно обработкой сигналов и просто заглянул из любопытства. А у вас лишь краткое понятное не всем предложение:
> При спектральном анализе через (обычно быстрое) дискретное преобразование Фурье анализируемый блок данных как бы «зацикливается», что приводит к разрыву на краях и искажению спектра:
Ну и стоило бы во вступлении объяснить, где это вообще применяется и зачем. Как я понимаю — при какой-то цифровой обработке сигналов, либо для добавления эффектов к звуковому сигналу, либо может быть для обработки радиосигнала.
И интересно, где вообще нужны нестандартные оконные функции, особенно несимметричной формы?
И еще интересно, а почему оконные функции не делают в виде скругленного с краев прямоугольного импульса, чтобы почти вся она равнялась единице и вносила минимум искажений в сигнал? А то ваши оконные функции похожи на горки и сигнал без изменений остается только в серединке.
И еще вопрос, может вы знаете ответ, раз уж занимаетесь обработкой сигналов. Если есть сигнал неизвестного вида, который может содержать частоту X + шумы и щелчки, и мы хотели бы получить на выходе амплитуду этой частоты X в сигнале, то есть увидеть, где она есть, где ее нет, где ее больше — есть какой-то готовый простой алгоритм, без вычисления FFT? Какой-то простой фильтр, может быть? Нужно для определения задержки прохождения сигнала через звуковую карту и ее драйвера.
> При спектральном анализе через (обычно быстрое) дискретное преобразование Фурье анализируемый блок данных как бы «зацикливается», что приводит к разрыву на краях и искажению спектра:
Ну и стоило бы во вступлении объяснить, где это вообще применяется и зачем. Как я понимаю — при какой-то цифровой обработке сигналов, либо для добавления эффектов к звуковому сигналу, либо может быть для обработки радиосигнала.
И интересно, где вообще нужны нестандартные оконные функции, особенно несимметричной формы?
И еще интересно, а почему оконные функции не делают в виде скругленного с краев прямоугольного импульса, чтобы почти вся она равнялась единице и вносила минимум искажений в сигнал? А то ваши оконные функции похожи на горки и сигнал без изменений остается только в серединке.
И еще вопрос, может вы знаете ответ, раз уж занимаетесь обработкой сигналов. Если есть сигнал неизвестного вида, который может содержать частоту X + шумы и щелчки, и мы хотели бы получить на выходе амплитуду этой частоты X в сигнале, то есть увидеть, где она есть, где ее нет, где ее больше — есть какой-то готовый простой алгоритм, без вычисления FFT? Какой-то простой фильтр, может быть? Нужно для определения задержки прохождения сигнала через звуковую карту и ее драйвера.
+2
пояснений немножечко не хватает. Вы пишете с расчетом на читателя, который прекрасно разбирается в оконных функциях, а наверно, стоило бы немного пояснить подробнее, зачем они нужны, для тех, кто не занимается ежедневно обработкой сигналов и просто заглянул из любопытстваПояснения к статье должны быть достаточно краткими для того, чтобы не отвлекать от сути. Я исходил из того, что если читатель не знаком с обработкой сигналов, то статью можно рассматривать просто как математическую задачу с решением.
почему оконные функции не делают в виде скругленного с краев прямоугольного импульса, чтобы почти вся она равнялась единице и вносила минимум искажений в сигнал?Потому что умножение сигнала на оконную функцию равносильно свёртке их спектров, и чем больше окно «квадратное», тем выше уровень боковых лепестков после FFT, что затрудняет спектральный анализ.
А то ваши оконные функции похожи на горки и сигнал без изменений остается только в серединке.Процент перекрытия может быть и меньше 50%. Я не стал заострять на этом внимание, потому что это казалось очевидным (каюсь):

0
И еще вопрос, может вы знаете ответ, раз уж занимаетесь обработкой сигналов. Если есть сигнал неизвестного вида, который может содержать частоту X + шумы и щелчки, и мы хотели бы получить на выходе амплитуду этой частоты X в сигнале, то есть увидеть, где она есть, где ее нет, где ее больше — есть какой-то готовый простой алгоритм, без вычисления FFT? Какой-то простой фильтр, может быть? Нужно для определения задержки прохождения сигнала через звуковую карту и ее драйвера.На мой взгляд, вопрос некорректно поставлен. Для определения задержки прохождения сигнала через звуковую карту и ее драйвера не нужно анализировать амплитуду частот, нужно обеспечить точку отсчёта и прогонять единичный импульс или ЛЧМ. Задача достаточно сложная, чтобы можно было дать на неё исчерпывающий ответ в комментарии.
0
Ну, это слишком просто и неинтересно. У нас могут быть посторонние шумы и искажения, так как вход и выход не соединены кабелем, а акустической связью через динамики/наушники и микрофон с неизвестными характеристиками.
0
А чем FFT не устраивает? Медленно считается? Если нужна только одна частота (т.е. одна точка на дискретном спектре), то можно считать дискретное преобразование Фурье для одной частоты. Сложность FFT — O(n * log (n)), а расчёта одной точки спектра «в лоб» — O(n), т.е. для очень узких фильтров (при больших n) будет в несколько раз быстрей.
Но учтите, что чем точней вам надо получить частоту, тем более длинную реализацию сигнала (окно) надо брать. Это принципиальное ограничение, не важно используете FFT (хотя ресурсов на расчёт FFT тоже надо больше), «железные» фильтры или ещё что.
Так что узкополосный сигнал может быть не самым удачным выбором, если надо измерять время. Как написал Refridgerator, лучше мощный импульсный сигнал или какой-то более сложный с широким спектром (ЛЧМ или ещё что).
Но учтите, что чем точней вам надо получить частоту, тем более длинную реализацию сигнала (окно) надо брать. Это принципиальное ограничение, не важно используете FFT (хотя ресурсов на расчёт FFT тоже надо больше), «железные» фильтры или ещё что.
Так что узкополосный сигнал может быть не самым удачным выбором, если надо измерять время. Как написал Refridgerator, лучше мощный импульсный сигнал или какой-то более сложный с широким спектром (ЛЧМ или ещё что).
0
И интересно, где вообще нужны нестандартные оконные функции, особенно несимметричной формы?При нелинейной обработке сигнала через FFT результат сильно зависит от оконной функции. Если после обработки возникает артефакт в виде реверберации или «звона», то несимметричная форма окна позволяет его сфокусировать в правой части импульса, что может дать более естественное звучание. Отличия те же, что и между фазолинейными и минимально-фазовыми фильтрами.
0
Например, с их помощью я делал генератор шума дождя — из записи дождя ограниченной продолжительности извлекал небольшие куски со случайным смещением и соединял их заново (в 4-х каналах), чтобы не слушать бесконечно одно и то же и получить объёмный звук. Это позволяло также настраивать «плотность» звука, смешивая в разных пропорциях разные части записи.
+1
По поводу определения неизвестной частоты в сигнале, возможно Generalized Harmonic Analysis то что вы ищете, например статья «Fast and Accurate Generalized Harmonic Analysis Using Newton’s Method». Ну и пользуясь случаем порекламирую библиотечку, которую как раз начал писать по этой статье, libgha
Идея там такая, сначала через FFT грубо ищем максимум, потом используя метод Ньютона уточняем частоту и фазу.
Работает это в предположении что в сигнале нет двух синусоид частоты которых расположены ближе частотного разрешения FFT с заданным окном.
Идея там такая, сначала через FFT грубо ищем максимум, потом используя метод Ньютона уточняем частоту и фазу.
Работает это в предположении что в сигнале нет двух синусоид частоты которых расположены ближе частотного разрешения FFT с заданным окном.
0
И еще вопрос, может вы знаете ответ, раз уж занимаетесь обработкой сигналов. Если есть сигнал неизвестного вида, который может содержать частоту X + шумы и щелчки, и мы хотели бы получить на выходе амплитуду этой частоты X в сигнале, то есть увидеть, где она есть, где ее нет, где ее больше — есть какой-то готовый простой алгоритм, без вычисления FFT? Какой-то простой фильтр, может быть? Нужно для определения задержки прохождения сигнала через звуковую карту и ее драйвера.
Посмотрите алгоритм Гёрцеля
0
Спасибо, интересная статья. Взял на заметку.
А в чем вы рисовали графики?
0
Не только графики, но и все вычисления сделаны в Wolfram Mathematica, в конце статьи есть ссылка на исходник. Код для графиков там скрыт по умолчанию, для открытия нужно выделить ячейку серым цветом над графиком и в меню Cell->Cell Properties->Open поставить галочку.
0
За счёт симметричности функции косинуса при сложении они суммируются в единицу:
А какое сложение используется?
Или имеется ввиду, что будет единица от первого «бугра» до последнего?
0
Совершенно случайно узнал, что в Vorbis (аудиокодек с потерями) для двойного наложения с 50%-ым перекрытием используется вот такое вот хитрое окно:

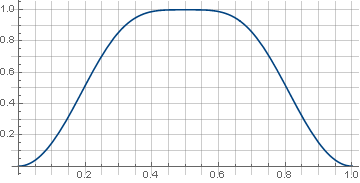
Для обнуления 1-ой производной они используют модуляцию аргумента. Круто.
Не удержался и добавил модуляцию модуляции — и обнулилась не только 2-ая производная, но и 3-я:
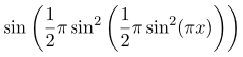
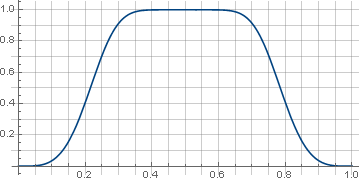
Правда, преобразование Фурье (аналитическое) от таких окон посчитать не получилось.
Wolfram с большим скрипом таки выдал результат на первое окно:
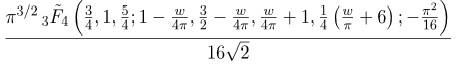
А вот второе уже никак.


Для обнуления 1-ой производной они используют модуляцию аргумента. Круто.
Не удержался и добавил модуляцию модуляции — и обнулилась не только 2-ая производная, но и 3-я:


Wolfram с большим скрипом таки выдал результат на первое окно:

А вот второе уже никак.
+1
В ATRAC3 (https://wiki.multimedia.cx/index.php/ATRAC3#Encoding_algorithm) используются разные окна при кодировании и декодировании, можете прокомментировать такое решение?
0
Правильно понял, речь об этих окнах?


+1
Да, они самые.
Наверно, нужно добавить, там так же используется mdct (как и в большенстве аудиокодеков).
Наверно, нужно добавить, там так же используется mdct (как и в большенстве аудиокодеков).
0
Для начала нужно привести всё к удобочитаемому виду, так как из кода от FFmpeg вообще ничего не понятно, особенно в строке w = 0.5 * (wi * wi + wj * wj). Вероятно, таким образом авторы пытались оптимизировать вычисления (хотя в этом нет никакого смысла, поскольку вызывается эта функция один раз и тормозить там вообще нечему).
Первым делом я посмотрел, что рисует (wi * wi + wj * wj), и получилась всё та же синусоида, только удвоенной частоты.Таким образом, если нормировать окно к (-1,1), то получим формулу
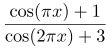
Но поскольку окно накладывается два раза — то итоговое окно будет представлять из себя произведение входного окна на выходное, а именно

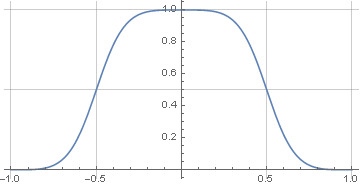
Тут уже хорошо видно, что оно симметричное и с перекрытием в 50% суммируется в единицу.
Вероятно, авторы очень сильно хотели, чтобы на входе было именно косинусоидальное окно — исходя из предположения, что влияние его на спектр сигнала будет минимальным (потому что при умножении сигнала на окно происходит свёртка их спектров) и это обеспечит лучшие возможности по сжатию данных.
Отдельный интересный вопрос, как эта формула выводилась — потому что деление на косинус удвоенной частоты вообще не очевидно. Смещение 3 в знаменателе могло быть найдено решением уравнения

Или вообще изначально это была совсем другая формула, которая в итоге сократилась до этой.
код
static av_cold void init_imdct_window(void)
{
int i, j;
for (i = 0, j = 255; i < 128; i++, j--)
{
float wi = sin(((i + 0.5) / 256.0 - 0.5) * M_PI) + 1.0;
float wj = sin(((j + 0.5) / 256.0 - 0.5) * M_PI) + 1.0;
float w = 0.5 * (wi * wi + wj * wj);
mdct_window[i] = mdct_window[511 - i] = wi / w;
mdct_window[j] = mdct_window[511 - j] = wj / w;
}
}Первым делом я посмотрел, что рисует (wi * wi + wj * wj), и получилась всё та же синусоида, только удвоенной частоты.Таким образом, если нормировать окно к (-1,1), то получим формулу

Но поскольку окно накладывается два раза — то итоговое окно будет представлять из себя произведение входного окна на выходное, а именно


Тут уже хорошо видно, что оно симметричное и с перекрытием в 50% суммируется в единицу.
Вероятно, авторы очень сильно хотели, чтобы на входе было именно косинусоидальное окно — исходя из предположения, что влияние его на спектр сигнала будет минимальным (потому что при умножении сигнала на окно происходит свёртка их спектров) и это обеспечит лучшие возможности по сжатию данных.
Отдельный интересный вопрос, как эта формула выводилась — потому что деление на косинус удвоенной частоты вообще не очевидно. Смещение 3 в знаменателе могло быть найдено решением уравнения

Или вообще изначально это была совсем другая формула, которая в итоге сократилась до этой.
+1
Спасибо! Буду обдумывать.
А подскажите еще, утверждение:
А подскажите еще, утверждение:
потому что при умножении сигнала на окно происходит свёртка их спектровтак же верно и для mdct?
0
На всякий случай хочу добавить, что косинусное окно вовсе не является наилучшим. При таком подходе (разных окнах на вход и выход) на входе можно использовать вообще практически любое окно — а окно на выходе получать делением желаемого результирующего на входное. Например, при использовании окна Блэкмана


и того же результирующего окна
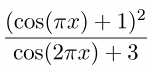
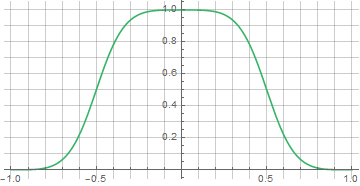
на выходе получим окно




и того же результирующего окна


на выходе получим окно


0
Я нашёл, откуда взялась формула
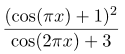
С большой долей вероятности, она взялась из формулы

где f(x):=

При n=1 получим обычное косинусоидальное окно, при n=2 — вышеозначенное (после упрощения), при бо́льших n — всё более «квадратное» окно. Вместо синуса можно брать и другие функции, которые пересекают центр координат и имеют там нулевые производные (например, параболу) — только они не будут обладать зеркальной симметрией по умолчанию, и её нужно будет реализовывать отдельно:


С большой долей вероятности, она взялась из формулы

где f(x):=

При n=1 получим обычное косинусоидальное окно, при n=2 — вышеозначенное (после упрощения), при бо́льших n — всё более «квадратное» окно. Вместо синуса можно брать и другие функции, которые пересекают центр координат и имеют там нулевые производные (например, параболу) — только они не будут обладать зеркальной симметрией по умолчанию, и её нужно будет реализовывать отдельно:

0
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Проектирование оконных функций, суммирующихся в единицу с заданным уровнем перекрытия