Привет странники. Мы как путешественники по своим мыслям, и анализаторы своего состояния, должны понимать где хорошо, а где иначе, где же именно мы находимся, вот к этому хочу привлечь внимание читателей.
Как мы складываем цепочки мыслей, последовательно?, предполагая вывод каждого шага, контролируя поток управления и состояние ячеек в памяти? Или просто описав постановку задачи, указывать программе какую именно задачу требуется решать, и этого достаточно для составления всех программ. Не превращать кодирование в поток команд, которые изменят внутреннее состояние системы, а выражать принцип, как понятие сортировки, ведь не обязательно представлять себе, что там за алгоритм прячется, просто нужно пожелать получить отсортированные данные. Не зря президент Америки может упомянуть о Пузырьке, он высказывает мысль о том, что он что-то понял в программировании. Он всего лишь узнал о том, что есть алгоритм сортировки, и данные в таблице, на его рабочем столе, сами по себе не могут выстроиться, каким-то волшебным образом, в алфавитном порядке.
Это представление, о том, что я хорошо отношусь к декларативному способу выражения мыслей, а выражать все последовательностью команд и переходов между ними, мне кажется архаичным и устаревшим, ведь так делали наши деды, деды соединяли проводками контакты на коммутационной панели и получали мигание лампочек, а у нас монитор и распознавание голоса, как находясь на таком уровне эволюции можно все еще задумываться, о следовании команд… Мне кажется, если выражать программу логическим языком, она будет выглядеть понятнее, и это можно произвести в технологию, на это была сделана ставка еще в 80-х.
Что же, введение затянулось....
Попробую, для начала, пересказать механизм быстрой сортировки. Для сортировки списка нужно его разбить на два подсписка и соединить отсортированный один подсписок с другим отсортированным подсписком.
Операция разбить должна уметь превращать список в два подсписка, один из них содержит все элементы менее опорного, а второй список содержит только большие элементы. Выражая это на Эрланге пишут всего лишь две строки:
qsort([])->[];
qsort([H|T])->qsort([X||X<-T,X<H])++[H|qsort([X||X<-T,X>=H])].Вот такие выражения результата мыслительного процесса мне интересны.
Представлять описание принципа сортировки в императивном виде труднее. Разве может быть преимущество у такого способа программирования, и тут как ты его не назови, хоть там си-плас-плас, хоть фортран. Не потому ли яваскрипт, и все веяния лямбда-функций в новых стандартах всех языков — это подтверждение неудобства алгоритмичности.
Попробую провести эксперимент, что бы убедиться в преимуществах одного подхода и другого, протестировать их. Попробую показать, что декларативную запись определения сортировки и ее же алгоритмическую запись можно сопоставить по производительности и сделать вывод, как правильнее формулировать программы. Может это подтолкнет отложить на полку программирование через алгоритмы и потоки команд, как просто устаревшие подходы, пользоваться которыми совсем не актуально, ведь не менее модно выражаться на хаскеле или на кложуре. И может не только фэ-шарп может придавать программам ясный и компактный вид?
Воспользуюсь Питоном для демонстрации, так как в нем есть несколько парадигм, и это совсем не си++ и уже не лисп. Можно написать ясную программу в разной парадигме:
Сортировка 1
def qsort(S):
if S==[]:return []
H,T=S[0],S[1:]
return qsort([X for X in T if X<T])+[H]+qsort([X for X in T if X>=T]) Словами можно произнести вот так: сортировка берет первый элемент как базовый, а потом все меньшие его сортируются и соединяются со всеми большими его, перед этим отсортированными.
А может такое выражение работать быстрее, чем сортировка написанная в топорном виде перестановки каких-то там, рядом стоящих или нет элементов. Разве можно выразить это лаконичнее, и потребовать для этого не так много слов. Попробуйте сформулировать вслух принцип сортировки пузырьком и изложить его президенту США, ведь так ему и достались эти сакральные данные, он узнавал про алгоритмы и его выложили, например, вот так: Для того чтобы отсортировать список, нужно взять пару элементов, сравнить их между собой и если первый более второго, то их необходимо обменять местами, переставить между собой, и далее нужно повторять поиск пар таких элементов с самого начала списка, пока перестановки не закончатся.
Да, принцип сортировки пузырька, даже звучит длиннее, чем версия быстрой сортировки, но преимущество второй не только в краткости записи, а и в ее скорости работы, выражение этой же быстрой сортировки, сформулированное алгоритмом будет ли быстрее чем версия декларативно выраженная? Может надо изменять взгляды на обучение программированию, надо как Японцы пробовали внедрять в школах преподавание Пролога и связанного с ним мышления. Можно системно переходить к удалению от алгоритмических языков выражения мыслей.
Сортировка 2
Для воспроизведения этого, пришлось обратиться к литературе, это формулировка от Хоара, пробую превращать это в Питон:
def quicksort(A, lo, hi):
if lo < hi:
p = partition(A, lo, hi)
quicksort(A, lo, p - 1)
quicksort(A, p + 1, hi)
return A
def partition(A, lo, hi):
pivot = A[lo]
i = lo - 1
j = hi + 1
while True
do: i= i + 1
while A[i] < pivot
do : j= j - 1
while A[j] > pivot
if i >= j: return j
A[i],A[j]=A[j],A[i]Восхищаюсь мыслью, тут нужен бесконечный цикл, он бы еще туда гоу-ту вставил)), вот уж шутники были.
Анализ
Вот теперь сделаем длинный список и заставим его отсортировать обоими методами, и поймем как быстрее, и эффективнее излагать свои мысли. Какой же из подходом воспринимать легче?
Создание списка из случайных чисел как отдельная проблема, вот так ее можно выразить:
def qsort(S):
if S==[]:return []
H,T=S[0],S[1:]
return qsort([X for X in T if X<H])+[H]+qsort([X for X in T if X>=H])
import random
def test(len):
list=[random.randint(-100, 100) for r in range(0,len)]
from time import monotonic
start = monotonic()
slist=qsort(list)
print('qsort='+str(monotonic() - start))
##print(slist)Вот такие замеры получены:
>>> test(10000)
qsort=0.046999999998661224
>>> test(10000)
qsort=0.0629999999946449
>>> test(10000)
qsort=0.046999999998661224
>>> test(100000)
qsort=4.0789999999979045
>>> test(100000)
qsort=3.6560000000026776
>>> test(100000)
qsort=3.7340000000040163
>>> Теперь повторю это в формулировке алгоритма:
def quicksort(A, lo, hi):
if lo < hi:
p = partition(A, lo, hi)
quicksort(A, lo, p )
quicksort(A, p + 1, hi)
return A
def partition(A, lo, hi):
pivot = A[lo]
i = lo-1
j = hi+1
while True:
while True:
i=i+1
if(A[i]>=pivot) or (i>=hi): break
while True:
j=j-1
if(A[j]<=pivot) or (j<=lo): break
if i >= j: return max(j,lo)
A[i],A[j]=A[j],A[i]
import random
def test(len):
list=[random.randint(-100, 100) for r in range(0,len)]
from time import monotonic
start = monotonic()
slist=quicksort(list,0,len-1)
print('quicksort='+str(monotonic() - start))Пришлось потрудиться над превращением исходного примера алгоритма из древних источников в Википедии. Значит так: нужно взять опорный элемент и располагать элементы в подмассиве так, чтобы слева оставались все менее, а справа все более его. Для этого обмениваем местами левый с правым элементом. Повторяем это для каждого подсписка разделенного индексом опорного элемента, если менять нечего заканчиваем.
Итого
Посмотрим, какая будет разница во времени для одного и того же списка, который сортируют двумя методами по очереди. Проведем 100 экспериментов, и постоим график:
import random
def test(len):
t1,t2=[],[]
for n in range(1,100):
list=[random.randint(-100, 100) for r in range(0,len)]
list2=list[:]
from time import monotonic
start = monotonic()
slist=qsort(list)
t1+=[monotonic() - start]
#print('qsort='+str(monotonic() - start))
start = monotonic()
slist=quicksort(list2,0,len-1)
t2+=[monotonic() - start]
#print('quicksort='+str(monotonic() - start))
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1,100),t1,label='qsort')
ax.plot(range(1,100),t2,label='quicksort')
ax.legend()
ax.grid(True)
plt.show()
test(10000)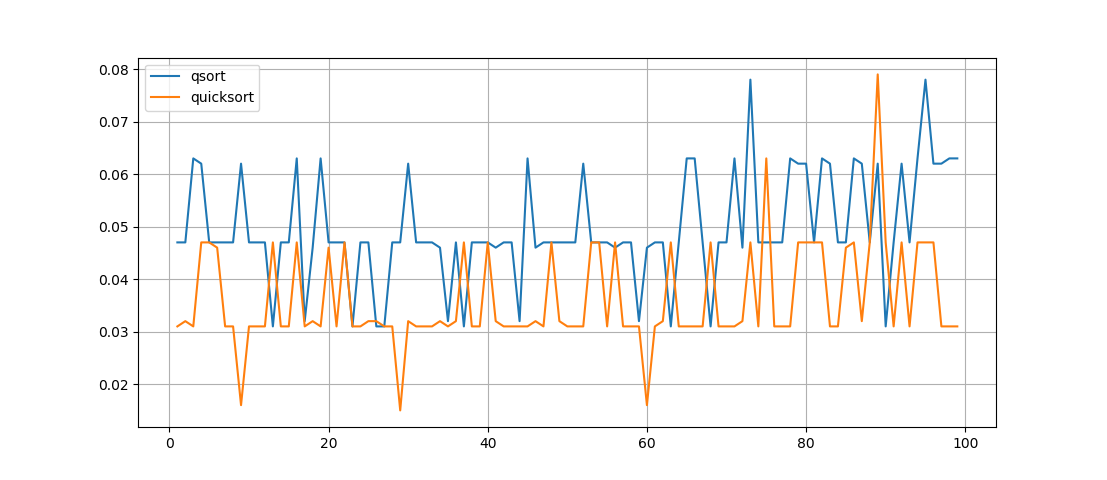
Что же тут видно — функция quicksort() работает быстрее, но ее запись не такая наглядная, хоть функция и рекурсивная, но понять работу перестановок производимых в ней, совсем не просто.
Ну что, какое выражение мысли сортировки более осознаваемо?
При небольшой разнице в производительности получаем такую разницу в объеме и сложности кода.
Может и правда хватит изучать императивные языки, а что для вас более привлекательно?
PS. А вот и Пролог:
qsort([],[]).
qsort([H|T],Res):-
findall(X,(member(X,T),X<H),L1), findall(X,(member(X,T),X>=H),L2),
qsort(L1,S1), qsort(L2,S2),
append(S1,[H|S2],Res).





