Вычислять факт попадания в играх на основе полученной меткости можно по разному:

Бонусы к меткости тоже можно реализовать по разному, вызывая тем самым у игроков раздражение по разными причинам.
Точно также по разному можно рассчитывать наносимый урон, особенно на основе дайсов (кубиков).
Все эти разные подходы влияют на игровой процесс: его сложность и предсказуемость. Каждый из них может оказаться удачным решением в зависимости от преследуемых целей, поэтому выгоднее всего делать выбор осознанно.
В статье будут представлены наглядные графики изменения реальных вероятностей в разных подходах, что позволит быстрее в них сориентироваться и принять лучшее решение.
Обычно, когда игроку сообщается, что меткость у персонажа равна 60%, то он воспринимает эту информацию как: «из 10 выстрелов я могу рассчитывать на 6 попаданий». И если из 10 попаданий он будет наблюдать 1 попадание вместо 6, то он почти наверняка посчитает, что случайность в игре поломана. Особенно сильно он в этом уверится, если такое случится на отрезке из 100 выстрелов. Чтобы избежать таких неприятностей, разработчики часто скрытно манипулируют с реальной вероятностью попадания (либо вообще отказываются от элемента случайности).
Например, в игре Fire Emblem: The Binding Blade для определения попадания с меткостью сравнивалось не одно случайное число, а среднее из двух случайных чисел [2].
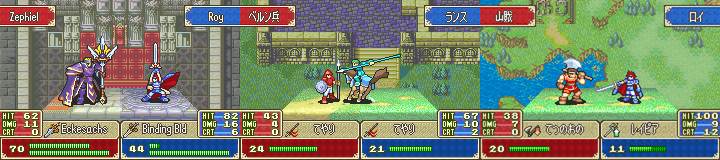
Результат этой манипуляции таков, что меткие атаки (>50%) попадают значительно чаще, чем им полагается при равномерном распределении, а неметкие (<50%) попадают значительно реже. Вот как меняется это распределение вероятностей:
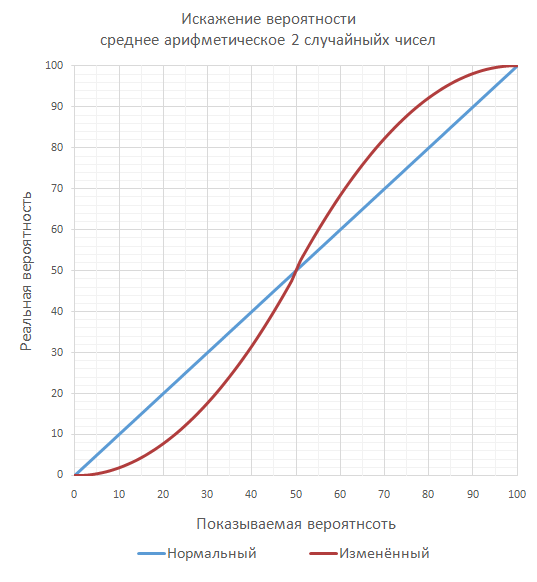
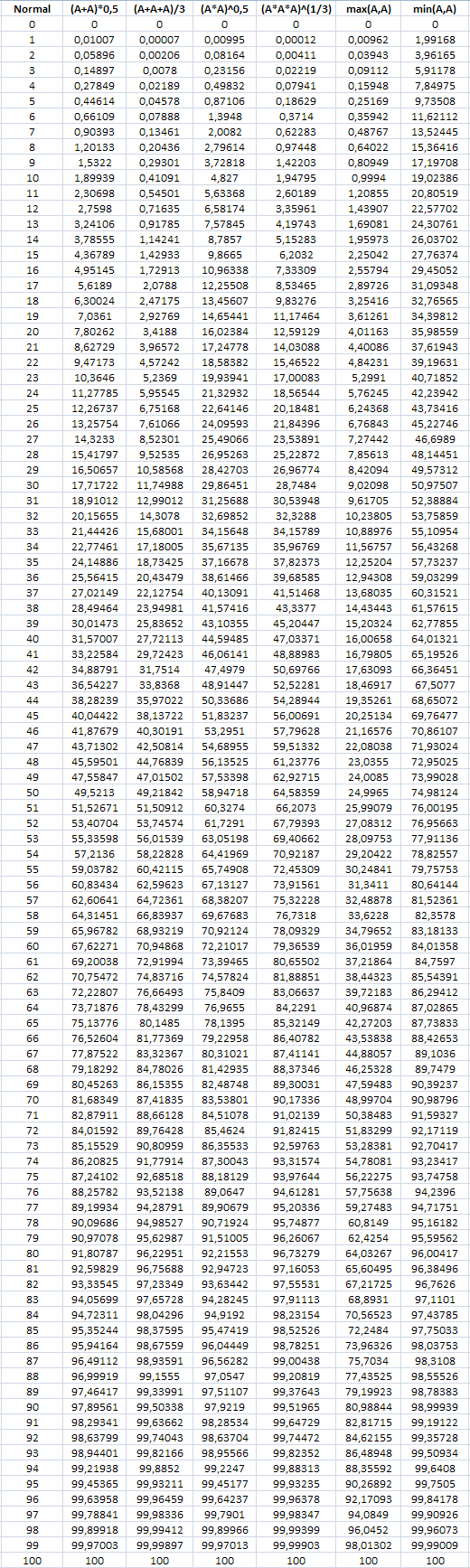
Для примера, при 10% показываемой меткости фактическая при этом является 1.9%. А при 75% фактическая будет 87.24%.
Но, если уж на то пошло, то менять меткость можно и многими другими способами.
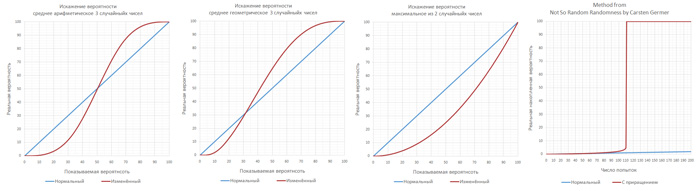
Например, можно взять среднее из 3 случайных чисел:
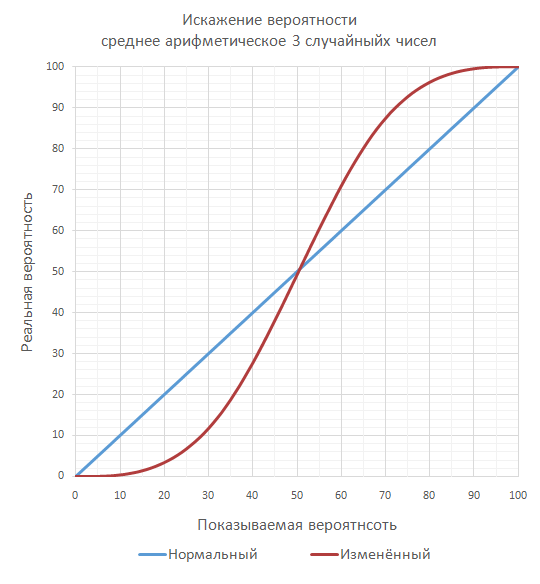
Искажение в результате этого становится еще более разительным: меткость 10% становится 0.41%; меткость 75% становится 92.69%.
Впрочем, среднее можно высчитывать и как среднее геометрическое. Вот какие изменения будут при среднем геометрическом из 2 случайных чисел:

Тут 10% превращаются в 4.83%, а 75% в 88.18%. Но, что самое интересное, переход происходит при 30%, а не при 50%, как в среднем арифметическом. Поэтому если Вам хочется уж точно быть уверенными, что у игрока всегда будет преимущество, то достаточно удостовериться, что его минимальная меткость никогда не будет ниже 30%, а у врагов она будет настолько низкой довольно часто (для врагов можно использовать и среднее арифметическое, или что-то еще более искаженное).
Среднее геометрическое из 3 чисел приводит примерно к тем же результатам, но только с большим разбросом:
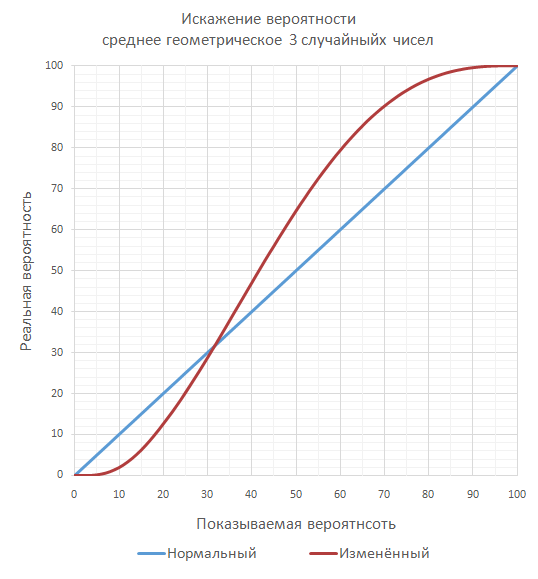
Тут 10% превращаются в 1.95%, а 75% в 93.98%.
Часто для усиления или ослабления каких-то навыков вводится и более простая манипуляция, когда из двух случайных чисел выбирается одно наибольшее или одно наименьшее:

В результате этого вероятность попадания меняется очень сильно. Например, при выбирании наименьшего числа меткость в 10% преобразуется в 19.02%, а меткость в 75% — в 93.75%.
Такой способ, например, используется в игре Neverwinter Nights в навыке «Скользкий разум», при котором в случае провала проверки на спасение производится повторная проверка на силу воли [3].
 Neverwinter Nights — Pixie Warrior [4]
Neverwinter Nights — Pixie Warrior [4]
В прошлой статье про манипуляции с вероятностями был показан метод для очень редких событий, где со временем увеличивалась вероятность события:
Вот как изменяется вероятность этого редкого события при использовании этого способа:
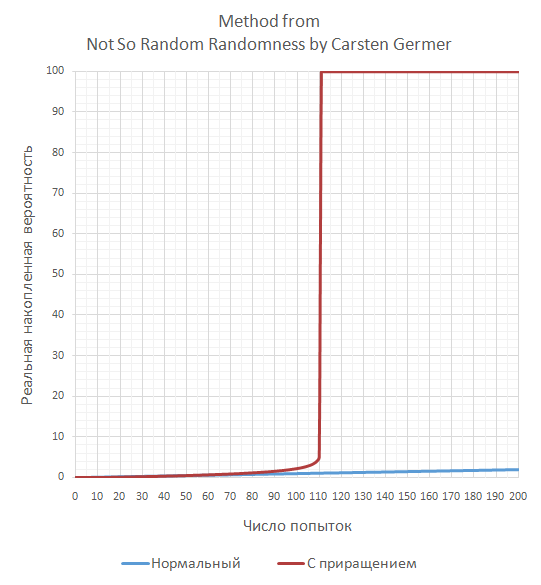
Как видим, в итоге ничего общего с вероятностью 1 к 10000, но для целей геймплея этого, возможно, было достаточно. Хотя больше похоже на ненамеренное сокрытие реальных вероятностей от самого разработчика, что может приводить к неправильным решениям в будущих доработках программы.
Ниже я привожу также изменение 1% события, что оно произойдёт хотя бы раз по мере роста числа попыток. Алгоритм искажения: первые 10 попыток — гарантированный промах. Затем с каждым промахом вероятность повышается на 1% (0,1% и 0,01%) до попадания. Потом всё с начала.

Впрочем, если ваша основная цель, как разработчика, гарантировать то, что пользователь в 1% событии не попадёт на серию из 1000 промахов подряд, то легче и прозрачнее будет после 200 промахов подряд выставлять 100% попадание. Это избавит вас от редких недоумений игроков и позволит оставить программный код лаконичнее и дружелюбнее для будущих доработок.
Если бонусов к меткости в игре немного и они легко контролируются разработчиком, то проще всего использовать самый простой подход с линейным увеличением меткости простым сложением с базовой величиной. Этот способ легче всего внедрить в игру и всегда понятен игрокам. При таком подходе возможно достижение 100% меткости, что не всегда соответствует планам разработчика.

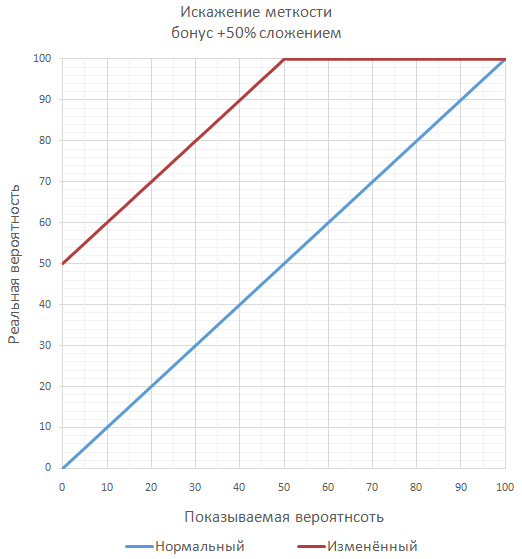
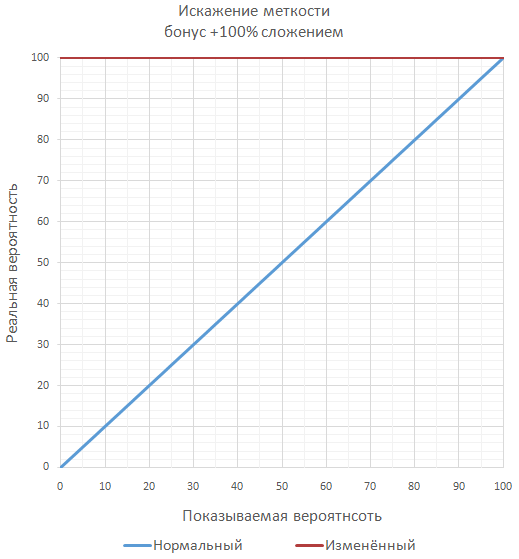
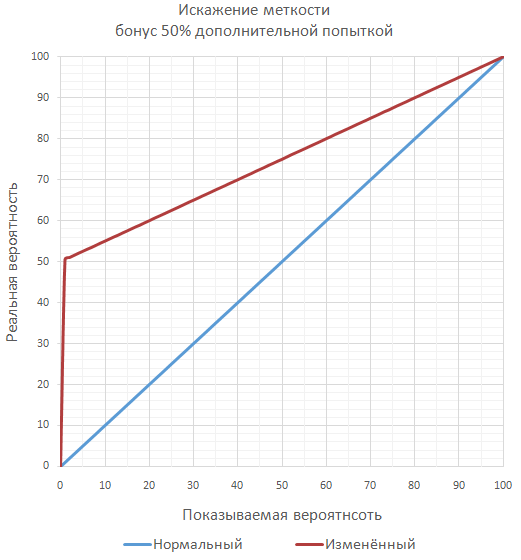
Если в игре планируется множество значительных бонусов к меткости, то, чтобы не переваливать за гарантированные 100% меткости, можно вычислять окончательную меткость как серию дополнительных бросков (чаще всего маловероятных по отдельности). Например, при меткости 70% и бонусе 50% окончательная вероятность попадания будет равна 85%, как проверка двух последовательных бросков, когда достаточно хотя бы одного попадания.


Немного экзотическим является подход по изменению сути бонуса к меткости на бонус уменьшения вероятности промаха.
Гарантирует, что всегда будет вероятность промаха при любом бонусе. Благодаря этому игра может давать бонусы к «меткости» больше 100%, хоть 1000%. И всё равно будет оставаться вероятность промаха. Но игрока это скорее может запутать, а, значит, и разочаровать.



Чаще всего используется подход с простым суммированием бонусов, как наиболее понятный для игрока, и лёгкий для реализации разработчиком.
Данный пункт целиком основан на наглядных данных публикации «Probability and Games: Damage Rolls from Red Blob Games [6]». Здесь я кратко представляю некоторые примеры и выводы этой публикации. В оригинальной статье Вы получите более детальные выводы и интерактивные графики распределений, а также интерактивно настраиваемые функции для подбора разных уникальных комбинаций.
Самый наглядный (но не единственный) пример различного подсчета урона дайсами представлен на основе вычисления урон при максимальном значении, равном 12. Результат может быть получен с помощью разных кубиков (например, если вы играете в настольную игру и каких-то специальных кубиков у вас нет):
1d12 — одним кубиком с 12 гранями

2d6 — двумя кубиками с 6 разными гранями
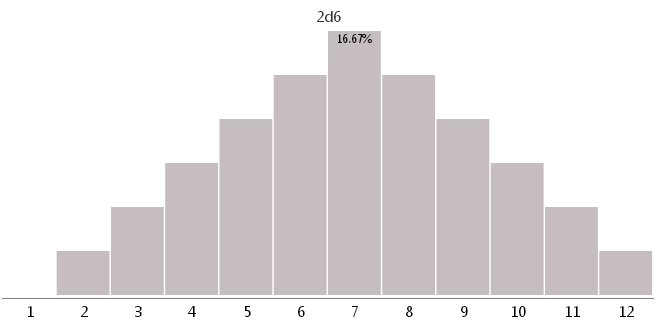
3d4 — тремя кубиками с 4 разными гранями
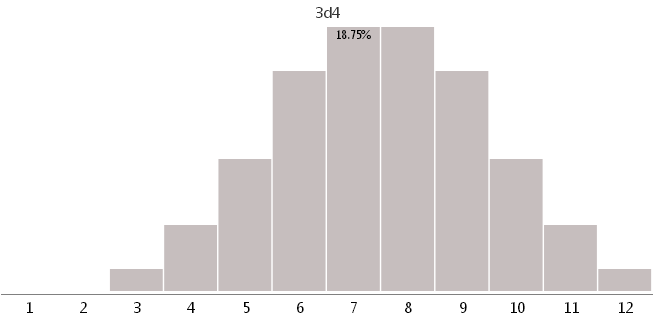
4d3 — четырьмя кубиками с 3 разными гранями
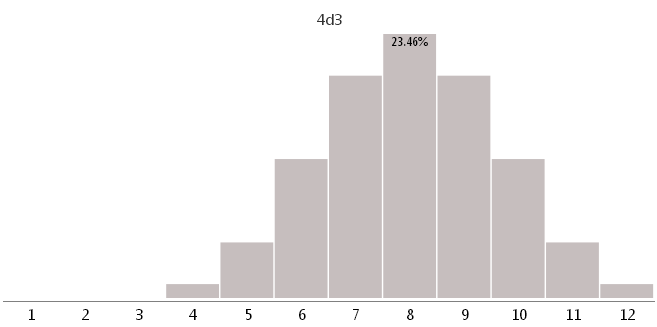
6d2 — шестью кубиками с 2 разными гранями
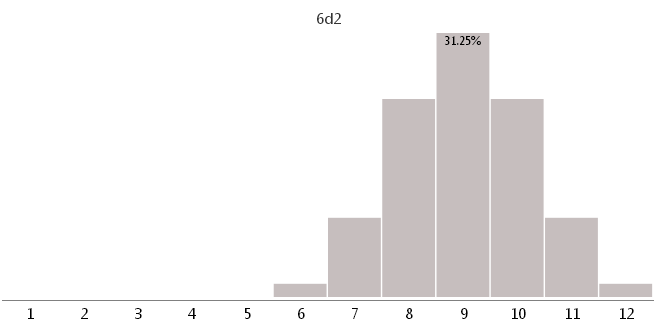
Как видно, использование неподходящих кубиков может очень сильно изменить игровой баланс.
Таким образом, были рассмотрены следующие темы:
Каждый из способов может быть полезен разработчику. Для игр с более казуальной аудиторией чаще выбирают щадящие алгоритмы, в которых вероятность успеха игрока завышается, а чтобы поднять азарт создаётся иллюзия маловероятной победы (подробнее в одной из прошлых статей: [7]).
1. Заблуждения игроков при оценке рисков. Контроль генератора случайных чисел в разработке.
2. Fire Emblem Wiki — Random Number Generator.
3. Neverwinter Nights 2 — Class Abilities — Slippery Mind.
4. Neverwinter Nights — Pixie Warrior.
5. «Not So Random Randomness» in Game Design and Programming.
6. Probability and Games: Damage Rolls from Red Blob Games.
7. Генерация Close call в играх: «На волосок от поражения» или «Чуть-чуть не победил».
- сравнивая с одним псевдослучайным числом (которое тоже можно получать по разному [1]);
- сравнивая с наибольшим или наименьшим из двух псевдослучайных чисел;
- сравнивая среднее из двух и более случайных чисел (среднее тоже можно считать по разному).
Бонусы к меткости тоже можно реализовать по разному, вызывая тем самым у игроков раздражение по разными причинам.
Точно также по разному можно рассчитывать наносимый урон, особенно на основе дайсов (кубиков).
Все эти разные подходы влияют на игровой процесс: его сложность и предсказуемость. Каждый из них может оказаться удачным решением в зависимости от преследуемых целей, поэтому выгоднее всего делать выбор осознанно.
В статье будут представлены наглядные графики изменения реальных вероятностей в разных подходах, что позволит быстрее в них сориентироваться и принять лучшее решение.
Манипуляции с меткостью
Обычно, когда игроку сообщается, что меткость у персонажа равна 60%, то он воспринимает эту информацию как: «из 10 выстрелов я могу рассчитывать на 6 попаданий». И если из 10 попаданий он будет наблюдать 1 попадание вместо 6, то он почти наверняка посчитает, что случайность в игре поломана. Особенно сильно он в этом уверится, если такое случится на отрезке из 100 выстрелов. Чтобы избежать таких неприятностей, разработчики часто скрытно манипулируют с реальной вероятностью попадания (либо вообще отказываются от элемента случайности).
Например, в игре Fire Emblem: The Binding Blade для определения попадания с меткостью сравнивалось не одно случайное число, а среднее из двух случайных чисел [2].
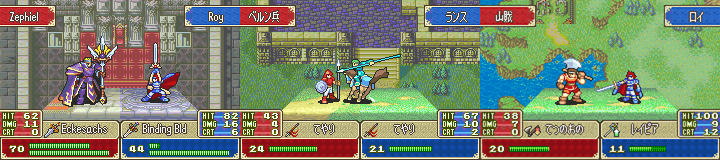
Результат этой манипуляции таков, что меткие атаки (>50%) попадают значительно чаще, чем им полагается при равномерном распределении, а неметкие (<50%) попадают значительно реже. Вот как меняется это распределение вероятностей:
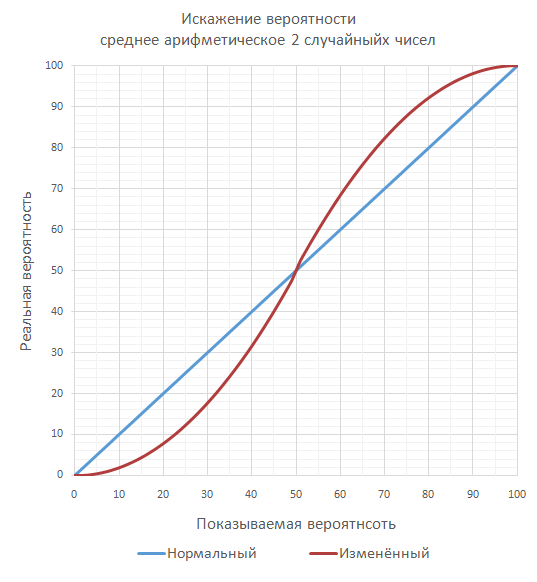
Для примера, при 10% показываемой меткости фактическая при этом является 1.9%. А при 75% фактическая будет 87.24%.
Но, если уж на то пошло, то менять меткость можно и многими другими способами.
Например, можно взять среднее из 3 случайных чисел:
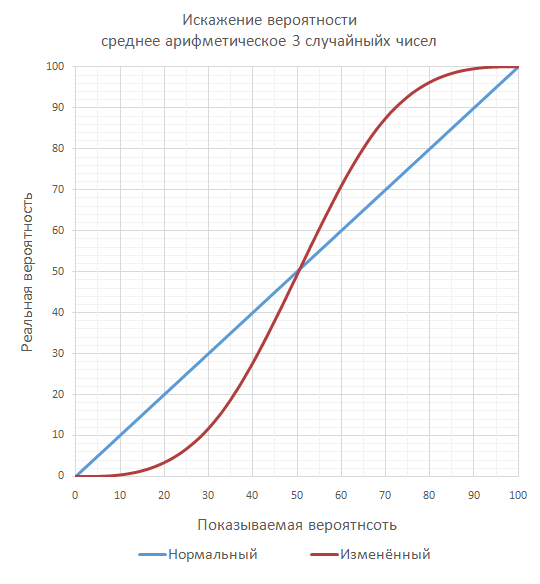
Искажение в результате этого становится еще более разительным: меткость 10% становится 0.41%; меткость 75% становится 92.69%.
Впрочем, среднее можно высчитывать и как среднее геометрическое. Вот какие изменения будут при среднем геометрическом из 2 случайных чисел:
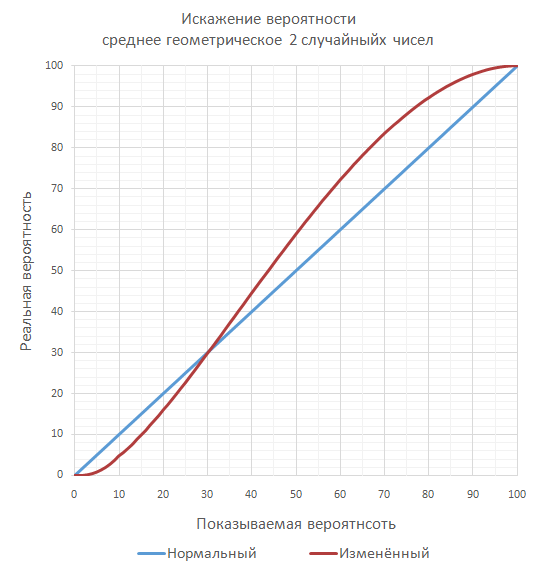
Тут 10% превращаются в 4.83%, а 75% в 88.18%. Но, что самое интересное, переход происходит при 30%, а не при 50%, как в среднем арифметическом. Поэтому если Вам хочется уж точно быть уверенными, что у игрока всегда будет преимущество, то достаточно удостовериться, что его минимальная меткость никогда не будет ниже 30%, а у врагов она будет настолько низкой довольно часто (для врагов можно использовать и среднее арифметическое, или что-то еще более искаженное).
Среднее геометрическое из 3 чисел приводит примерно к тем же результатам, но только с большим разбросом:

Тут 10% превращаются в 1.95%, а 75% в 93.98%.
Часто для усиления или ослабления каких-то навыков вводится и более простая манипуляция, когда из двух случайных чисел выбирается одно наибольшее или одно наименьшее:
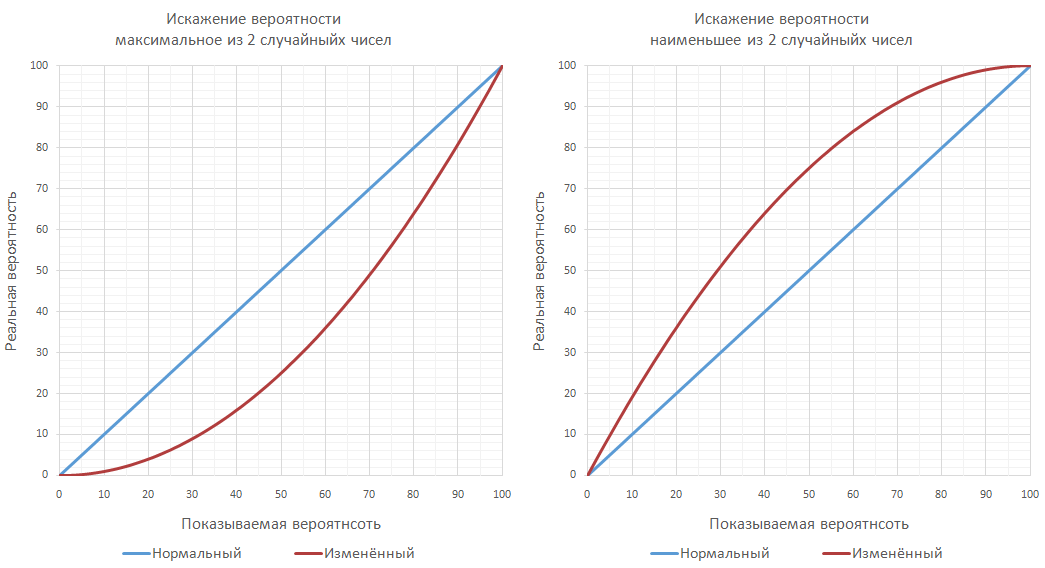
В результате этого вероятность попадания меняется очень сильно. Например, при выбирании наименьшего числа меткость в 10% преобразуется в 19.02%, а меткость в 75% — в 93.75%.
Такой способ, например, используется в игре Neverwinter Nights в навыке «Скользкий разум», при котором в случае провала проверки на спасение производится повторная проверка на силу воли [3].
Ниже приводится таблица искажения меткости при разных способах вычислений.
В прошлой статье про манипуляции с вероятностями был показан метод для очень редких событий, где со временем увеличивалась вероятность события:
Разработчик Carsten Germer использует функцию контролируемой случайности для редких и не только событий [5]. Например, чтобы гарантировать периодическое выпадение особо редкого бонуса с шансом 1 к 10000, он после каждого «промаха» увеличивает шансы по порядку: 1 к 9900; 1 к 9800; 1 к 9700… и так до фиксации события. А чтобы гарантировать отсутствие частых редкостей, он ввел дополнительную переменную, блокирующую срабатывание на 100% в течение 10 следующих проверок после прошлого срабатывания.Заблуждения игроков при оценке рисков [1]
Вот как изменяется вероятность этого редкого события при использовании этого способа:
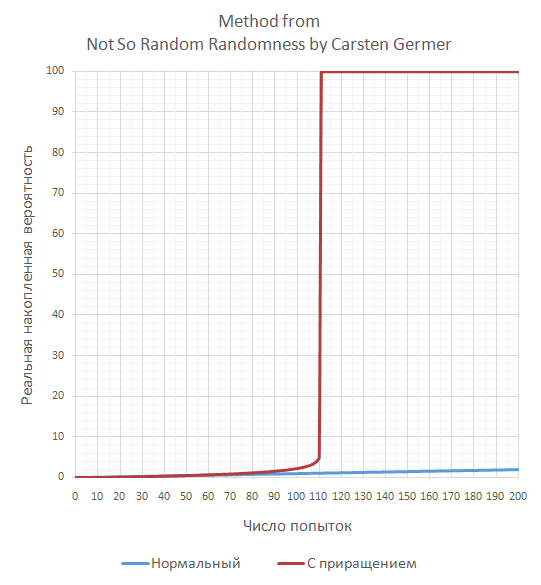
Как видим, в итоге ничего общего с вероятностью 1 к 10000, но для целей геймплея этого, возможно, было достаточно. Хотя больше похоже на ненамеренное сокрытие реальных вероятностей от самого разработчика, что может приводить к неправильным решениям в будущих доработках программы.
Ниже я привожу также изменение 1% события, что оно произойдёт хотя бы раз по мере роста числа попыток. Алгоритм искажения: первые 10 попыток — гарантированный промах. Затем с каждым промахом вероятность повышается на 1% (0,1% и 0,01%) до попадания. Потом всё с начала.
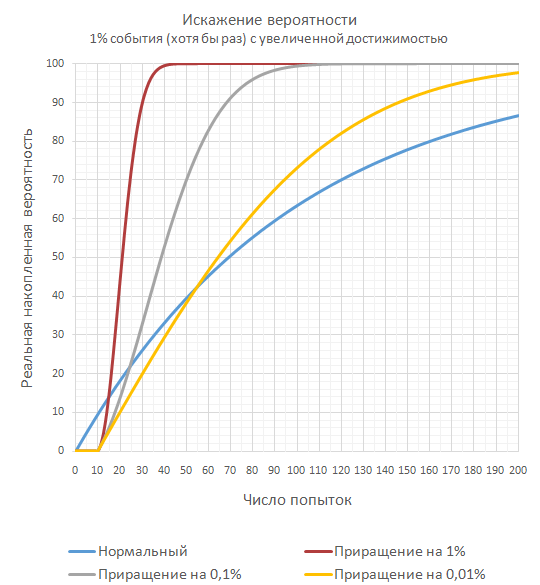
Впрочем, если ваша основная цель, как разработчика, гарантировать то, что пользователь в 1% событии не попадёт на серию из 1000 промахов подряд, то легче и прозрачнее будет после 200 промахов подряд выставлять 100% попадание. Это избавит вас от редких недоумений игроков и позволит оставить программный код лаконичнее и дружелюбнее для будущих доработок.
Разные способы начисления бонусов к меткости
Если бонусов к меткости в игре немного и они легко контролируются разработчиком, то проще всего использовать самый простой подход с линейным увеличением меткости простым сложением с базовой величиной. Этот способ легче всего внедрить в игру и всегда понятен игрокам. При таком подходе возможно достижение 100% меткости, что не всегда соответствует планам разработчика.
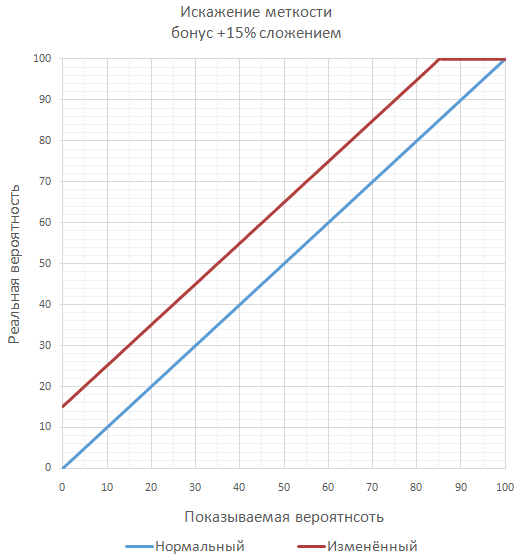
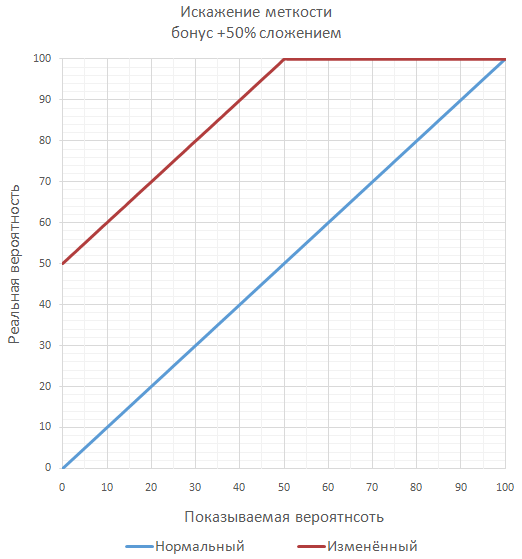
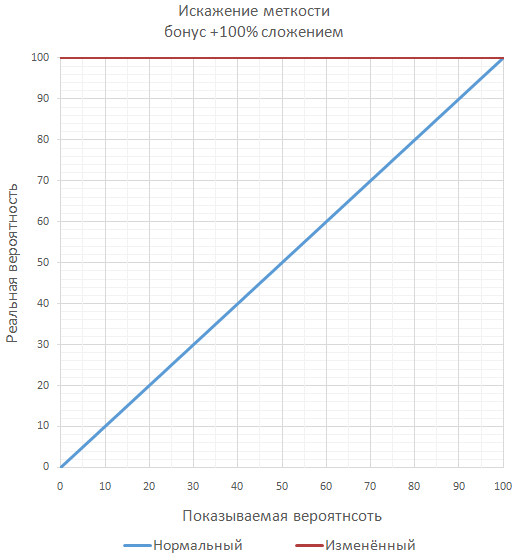
Если в игре планируется множество значительных бонусов к меткости, то, чтобы не переваливать за гарантированные 100% меткости, можно вычислять окончательную меткость как серию дополнительных бросков (чаще всего маловероятных по отдельности). Например, при меткости 70% и бонусе 50% окончательная вероятность попадания будет равна 85%, как проверка двух последовательных бросков, когда достаточно хотя бы одного попадания.
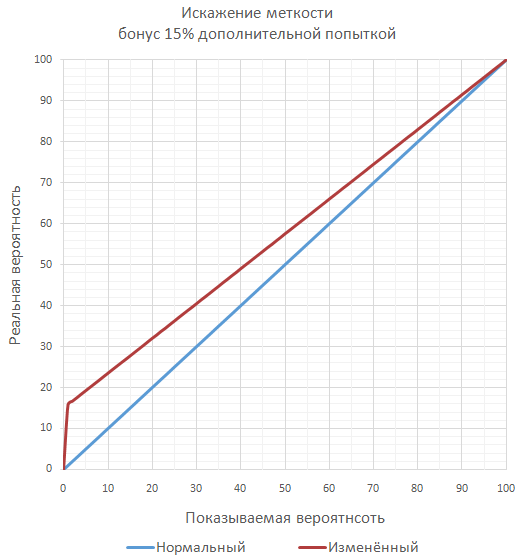
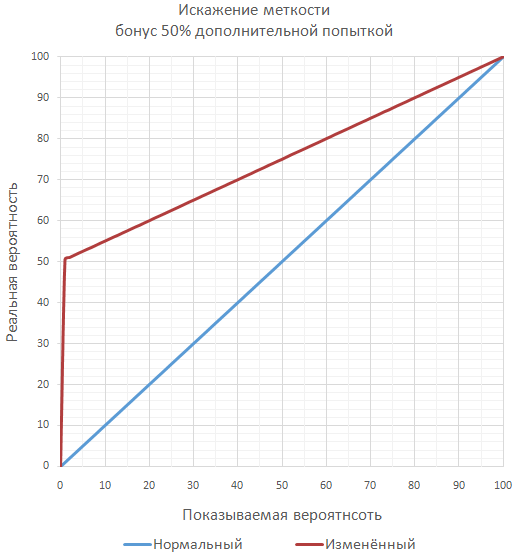
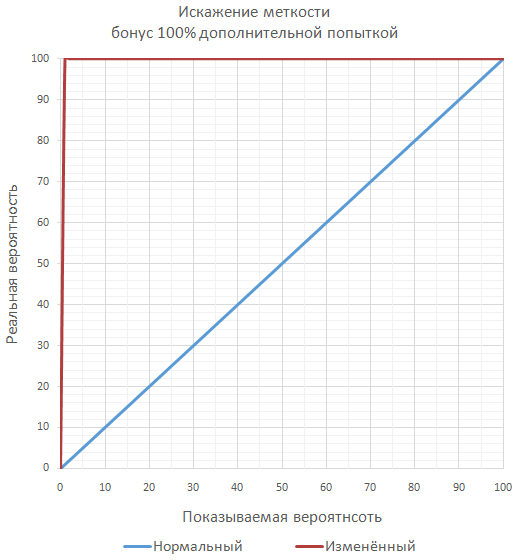
Немного экзотическим является подход по изменению сути бонуса к меткости на бонус уменьшения вероятности промаха.
// newAccuracy - новая меткость в %
// baseAccuracy - изначальная меткость в %
// bonusAccuracy - бонус к меткости в %
let newAccuracy = 100 - ( (1 - baseAccuracy * 0.01) / (1 + bonusAccuracy * 0.01) ) * 100;
Гарантирует, что всегда будет вероятность промаха при любом бонусе. Благодаря этому игра может давать бонусы к «меткости» больше 100%, хоть 1000%. И всё равно будет оставаться вероятность промаха. Но игрока это скорее может запутать, а, значит, и разочаровать.
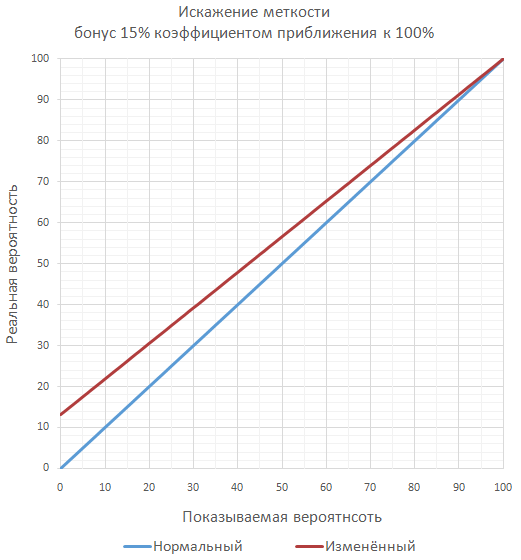
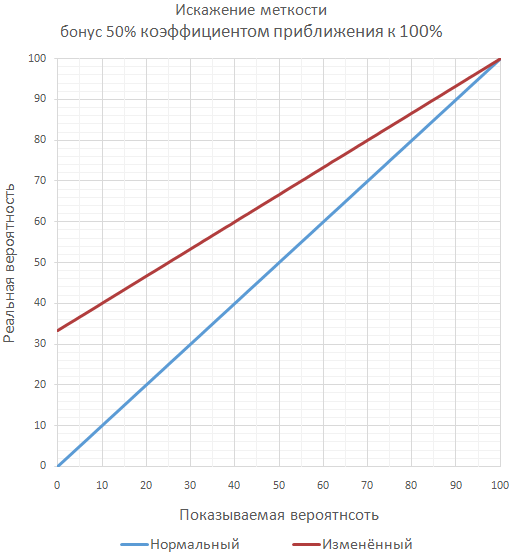
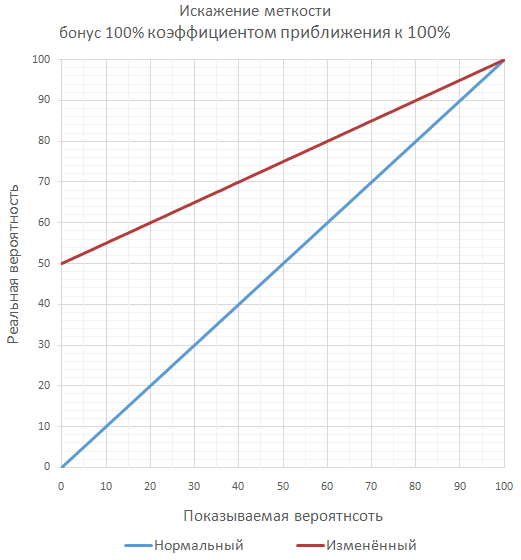
Чаще всего используется подход с простым суммированием бонусов, как наиболее понятный для игрока, и лёгкий для реализации разработчиком.
Распределение урона на основе дайсов
Данный пункт целиком основан на наглядных данных публикации «Probability and Games: Damage Rolls from Red Blob Games [6]». Здесь я кратко представляю некоторые примеры и выводы этой публикации. В оригинальной статье Вы получите более детальные выводы и интерактивные графики распределений, а также интерактивно настраиваемые функции для подбора разных уникальных комбинаций.
Самый наглядный (но не единственный) пример различного подсчета урона дайсами представлен на основе вычисления урон при максимальном значении, равном 12. Результат может быть получен с помощью разных кубиков (например, если вы играете в настольную игру и каких-то специальных кубиков у вас нет):
1d12 — одним кубиком с 12 гранями

2d6 — двумя кубиками с 6 разными гранями
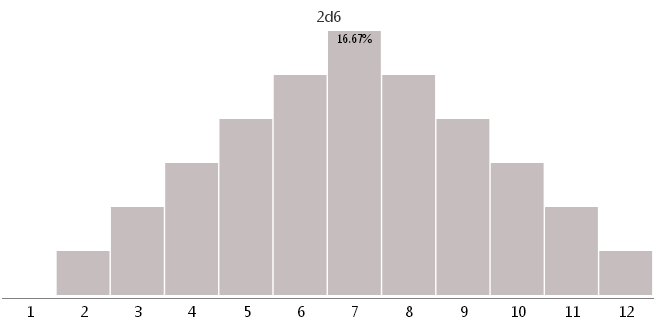
3d4 — тремя кубиками с 4 разными гранями
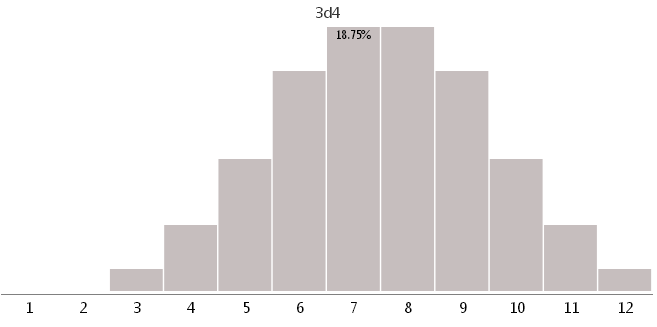
4d3 — четырьмя кубиками с 3 разными гранями
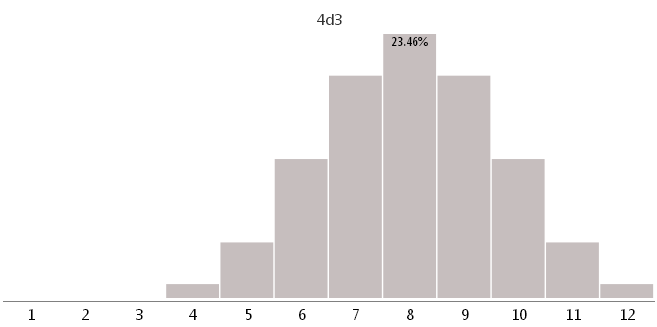
6d2 — шестью кубиками с 2 разными гранями
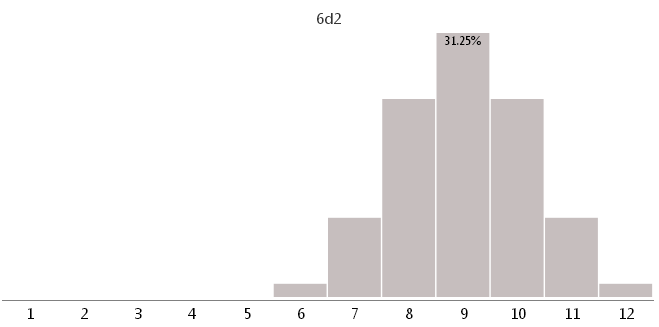
Как видно, использование неподходящих кубиков может очень сильно изменить игровой баланс.
Заключение
Таким образом, были рассмотрены следующие темы:
- манипуляции с меткостью с помощью разных способов её проверки;
- разные способы начисления бонусов к меткости;
- различное распределение урона на основе дайсов.
Каждый из способов может быть полезен разработчику. Для игр с более казуальной аудиторией чаще выбирают щадящие алгоритмы, в которых вероятность успеха игрока завышается, а чтобы поднять азарт создаётся иллюзия маловероятной победы (подробнее в одной из прошлых статей: [7]).
Список литературы
1. Заблуждения игроков при оценке рисков. Контроль генератора случайных чисел в разработке.
2. Fire Emblem Wiki — Random Number Generator.
3. Neverwinter Nights 2 — Class Abilities — Slippery Mind.
4. Neverwinter Nights — Pixie Warrior.
5. «Not So Random Randomness» in Game Design and Programming.
6. Probability and Games: Damage Rolls from Red Blob Games.
7. Генерация Close call в играх: «На волосок от поражения» или «Чуть-чуть не победил».






