Введение
На Habr были опубликованы несколько статей [1,2,3], прямо или косвенно касающиеся указанной темы. В связи с этим, нельзя не отметить публикацию [1] с названием “Математика на пальцах: линейно-квадратичный регулятор”, которая популярно поясняет принцип работы оптимального LQR контролера.
Мне захотелось продолжить указанную тему, рассмотрев практическое применения метода динамической оптимизации, но уже на конкретном примере средствами Python. Сначала пару слов о терминологии и методе динамической оптимизации.
Методы оптимизации делятся на статические и динамические. Объект управления находится в состоянии непрерывного движения под действием различных внешних и внутренних факторов. Следовательно, оценка результата управления дается за время управления Т, и это задача динамической оптимизации.
С помощью методов динамической оптимизации решаются задачи, связанные с распределением ограниченных ресурсов на протяжении некоторого промежутка времени, а целевая функция записывается в виде интегрального функционала.
Математическим аппаратом решения таких задач являются вариационные методы: классическое вариационное исчисление, принцип максимума Л.С. Понтрягина и динамическое программирование Р. Беллмана.
Анализ и синтез систем управления выполняется во временной, частотной областях и в пространстве состояний. Анализ и синтез систем управления в пространстве состояний введен в учебные программы, однако приведенные в учебных материалах методики с применением SQR контролера рассчитаны на применение Matlab и не содержат практически реализуемых примеров анализа.
Целью настоящей публикации является рассмотрение методики анализа и синтеза линейных систем управления в пространстве состояний на известном примере оптимизации системы управления электроприводом и летательным аппаратом средствами языка программирования Python.
Математическое обоснование метода динамической оптимизации
Для оптимизации используют критерии амплитудного (МО), симметричного (СО) и компромиссного оптимумов (КО).
При решении задач оптимизации в пространстве состояний, линейная стационарная система задана векторно — матричными уравнениями:
Интегральные критерии минимума расхода энергии на управление и максимального быстродействия задаются функционалами:
Закон управления u находится в форме линейной обратной связи по переменным состояния x или по переменным выхода у:
Такое управление минимизирует квадратичные критерии качества (2),(3). В соотношениях (1)÷(3) Q и R – симметричные положительно определенные матрицы размерностью [n×n]и[m×m] соответственно; К – матрица постоянных коэффициентов размерностью [m×n], на значения которых нет ограничений. Если входной параметр N опущен, он принимается нулевым.
Решение данной задачи, которая называется задачей линейной интегральной квадратичной оптимизации (LQR-оптимизации), в пространстве состояний определяется выражением:
где матрица Р должна удовлетворять уравнению Рикатти:
Критерии (2),(3) также противоречивы, так как для реализации первого слагаемого требуется источник бесконечно большой мощности, а для второго – источник бесконечно малой мощности. Это можно объяснить следующим выражением:
в котором является нормой
является мерой количества энергии, используемой для управления, это штраф за энергетические затраты системы.
От весовых матриц Q, R и N зависят ограничения соответствующих координат. Если какой-либо элемент этих матриц равен нулю, то соответствующая координата ограничений не имеет. На практике выбор значений матриц Q, R, N осуществляется методом экспертных оценок, проб, ошибок и зависит от опыта и знаний инженера-проектировщика.
Для решения подобных задач использовались следующие операторы MATLAB:
Модель объекта управления
Составляющие функционала:
где х0 – вектор начальных условий;
Особенности реализации метода динамической оптимизации средствами Python
Хотя в библиотеке Python Control Systems Library[4], есть функции: control.lqr, control.lyap, однако использование control.lqr возможно только при условии установки модуля slycot, которая является проблемой[5]. При использовании функции lyap в контексте задачи, оптимизации приводит к ошибке control.exception.ControlArgument: Q must be a symmetric matrix [6].
Поэтому, для реализации функций lqr() и lyap(), я использовал scipy.linalg:
from numpy import*
from scipy.linalg import*
def lqr(A,B,Q,R):
S =matrix(solve_continuous_are(A, B, Q, R))
K = matrix(inv(R)*(B.T*S))
E= eig(A-B*K)[0]
return K, S, E
P1=solve_lyapunov(NN,Ct*Q*C)Кстати, совсем отказываться от control не следует, поскольку функции step(),pole(), ss(),tf(),feedback(),acker(),place () и другие хорошо работают.
Пример LQR-оптимизации в электроприводе
(пример взят из публикации [7])Рассмотрим синтез линейно-квадратичного регулятора, удовлетворяющего критерию (2) для объекта управления, заданного в пространстве состояний матрицами:
В качестве переменных состояния рассматриваются:
При решении задачи принимаем матрицу Q диагональной. В результате моделирования установлено, что минимальные значения элементов матриц R= 84, а
Листинг программы (рис.1).
# -*- coding: utf8 -*-
from numpy import*
from control.matlab import *
from matplotlib import pyplot as plt
from scipy.linalg import*
def lqr(A,B,Q,R):
S =matrix(solve_continuous_are(A, B, Q, R))
K = matrix(inv(R)*(B.T*S))
E= eig(A-B*K)[0]
return K, S, E
# Коэффициенты объекта
A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]);
B=matrix([[2300], [0], [0]]);
C=eye(3)
D=zeros([3,1])
# Матрицы весовых коэффициентов
R=[[84]]
Q=matrix([[0.01, 0, 0],[0, 0.01, 0],[0, 0, 0.01]]);
# Синтез LQR-оптимального регулятора
[K,S,E]=lqr(A,B,Q,R)
# Вычисление составляющих функционала
N=A-B*K;
NN=N.T;
w=ss(N,B,C,D)
x0=matrix([[220], [147], [162]]);
Ct=C.T;
P1=solve_lyapunov(NN,Ct*Q*C)
Kt=K.T;
x0t=x0.T;
Jx=abs((x0t*P1*x0)[0,0])
P2=solve_lyapunov(NN,Kt*R*K);
Ju=abs((x0t*P2*x0)[0,0])
fig = plt.figure()
plt.suptitle('Переходные функции в системе управления при R = %s,\n\
$J_{x}$= %s; $J_{u}$ = %s,Q=[[0.01,0,0],[0, 0.01,0],[0,0,0.01]]'%(R[0][0],round(Jx,1),round(Ju,1)))
ax1 = fig.add_subplot(311)
y,x=step(w[0,0])
ax1.plot(x,y,"b")
plt.ylabel('$x_{1}$,B')
ax1.grid(True)
ax2 = fig.add_subplot(312)
y,x=step(w[1,0])
ax2.plot(x,y,"b")
plt.ylabel('$x_{2}$,A')
ax2.grid(True)
ax3 = fig.add_subplot(313)
y,x=step(w[2,0])
ax3.plot(x,y,"b")
plt.ylabel('$x_{3}$,$C^{-1}$')
ax3.grid(True)
plt.xlabel('Время, с.')
plt.show()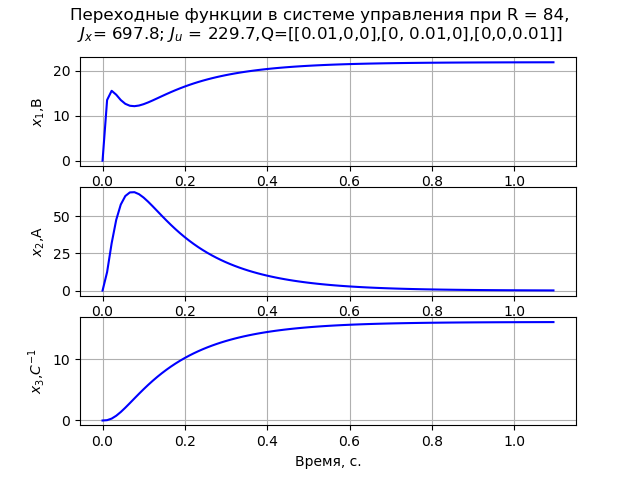
Рис. 1
Листинг программы (рис.2).
# -*- coding: utf8 -*-
from numpy import*
from control.matlab import *
from matplotlib import pyplot as plt
from scipy.linalg import*
def lqr(A,B,Q,R):
S =matrix(solve_continuous_are(A, B, Q, R))
K = matrix(inv(R)*(B.T*S))
E= eig(A-B*K)[0]
return K, S, E
# Коэффициенты объекта
A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]);
B=matrix([[2300], [0], [0]]);
C=eye(3)
D=zeros([3,1])
# Матрицы весовых коэффициентов
R=[[840]]
Q=matrix([[0.01, 0, 0],[0, 0.01, 0],[0, 0, 0.01]]);
# Синтез LQR-оптимального регулятора
[K,S,E]=lqr(A,B,Q,R)
# Вычисление составляющих функционала
N=A-B*K;
NN=N.T;
w=ss(N,B,C,D)
x0=matrix([[220], [147], [162]]);
Ct=C.T;
P1=solve_lyapunov(NN,Ct*Q*C)
Kt=K.T;
x0t=x0.T;
Jx=abs((x0t*P1*x0)[0,0])
P2=solve_lyapunov(NN,Kt*R*K);
Ju=abs((x0t*P2*x0)[0,0])
fig = plt.figure()
plt.suptitle('Переходные процессы в системе управления при R = %s,\n\
$J_{x}$= %s; $J_{u}$ = %s,Q=[[0.01,0,0],[0, 0.01,0],[0,0,0.01]]'%(R[0][0],round(Jx,1),round(Ju,1)))
ax1 = fig.add_subplot(311)
y,x=step(w[0,0])
ax1.plot(x,y,"b")
plt.ylabel('$x_{1}$,B')
ax1.grid(True)
ax2 = fig.add_subplot(312)
y,x=step(w[1,0])
ax2.plot(x,y,"b")
plt.ylabel('$x_{2}$,A')
ax2.grid(True)
ax3 = fig.add_subplot(313)
y,x=step(w[2,0])
ax3.plot(x,y,"b")
plt.ylabel('$x_{3}$,$C^{-1}$')
ax3.grid(True)
plt.xlabel('Время, с.')
plt.show()
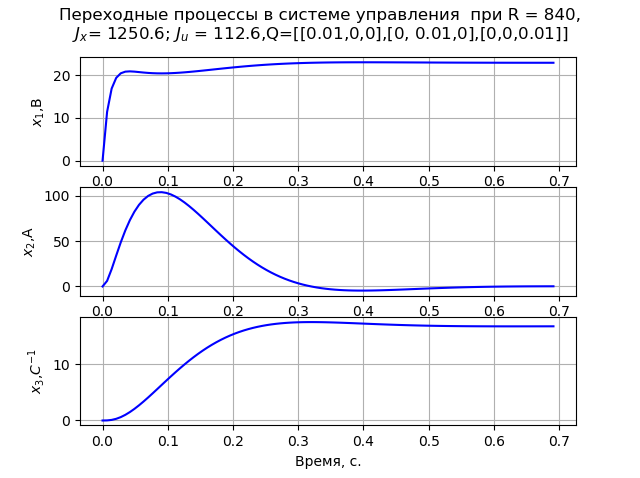
Рис. 2
Соответствующим выбором матриц R и Q можно уменьшить пусковой ток двигателя до допустимых значений, равных (2–2,5)Iном (рис. 3). Например, при R = 840 и
Q = ([[0.01,0,0],[0,0.88,0],[0,0,0.01]] его значение равно 292 А, а время переходного процесса при этих условиях – 1,57 с.
Листинг программы (рис.3).
# -*- coding: utf8 -*-
from numpy import*
from control.matlab import *
from matplotlib import pyplot as plt
from scipy.linalg import*
def lqr(A,B,Q,R):
S =matrix(solve_continuous_are(A, B, Q, R))
K = matrix(inv(R)*(B.T*S))
E= eig(A-B*K)[0]
return K, S, E
# Коэффициенты объекта
A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]);
B=matrix([[2300], [0], [0]]);
C=eye(3)
D=zeros([3,1])
# Матрицы весовых коэффициентов
R=[[840]]
Q=matrix([[0.01,0,0],[0,0.88,0],[0,0,0.01]]);
# Синтез LQR-оптимального регулятора
[K,S,E]=lqr(A,B,Q,R)
# Вычисление составляющих функционала
N=A-B*K;
NN=N.T;
w=ss(N,B,C,D)
x0=matrix([[220], [147], [162]]);
Ct=C.T;
P1=solve_lyapunov(NN,Ct*Q*C)
Kt=K.T;
x0t=x0.T;
Jx=abs((x0t*P1*x0)[0,0])
P2=solve_lyapunov(NN,Kt*R*K);
Ju=abs((x0t*P2*x0)[0,0])
fig = plt.figure()
plt.suptitle('Переходные процессы при допустимом пусковом токе R = %s,\n\
$J_{x}$= %s; $J_{u}$ = %s,Q=[[0.01,0,0],[0,0.88,0],[0,0,0.01]]'%(R[0][0],round(Jx,1),round(Ju,1)))
ax1 = fig.add_subplot(311)
y,x=step(w[0,0])
ax1.plot(x,y,"b")
plt.ylabel('$x_{1}$,B')
ax1.grid(True)
ax2 = fig.add_subplot(312)
y,x=step(w[1,0])
ax2.plot(x,y,"b")
plt.ylabel('$x_{2}$,A')
ax2.grid(True)
ax3 = fig.add_subplot(313)
y,x=step(w[2,0])
ax3.plot(x,y,"b")
plt.ylabel('$x_{3}$,$C^{-1}$')
ax3.grid(True)
plt.xlabel('Время, с.')
plt.show()
Рис.3
Во всех рассмотренных случаях обратные связи по напряжению и току являются отрицательными, а по скорости – положительными, что нежелательно по требованиям устойчивости. Кроме того, синтезированная система является астатической по заданию и статической по нагрузке. Поэтому рассмотрим синтез ПИ-регулятора в пространстве состояний с дополнительной переменной состояния
Исходную информацию представим в виде матриц:
Переходные процессы по заданию, соответствующие критерию МО, получены при R= 100, q11 = q22 = q33 =0.001 и q44 = 200. На рисунке 4 представлены переходные процессы переменных состояния, подтверждающие астатизм системы по заданию и по нагрузке.
Листинг программы (рис.4).
# -*- coding: utf8 -*-
from numpy import*
from control.matlab import *
from matplotlib import pyplot as plt
from scipy.linalg import*
def lqr(A,B,Q,R):
S =matrix(solve_continuous_are(A, B, Q, R))
K = matrix(inv(R)*(B.T*S))
E= eig(A-B*K)[0]
return K, S, E
# Коэффициенты объекта
A=matrix([[-100,0,0,0],[143.678, -16.667,-195.402,0],[0,1.046,0,0] ,[0,0,1,0]]);
B=matrix([[2300], [0], [0],[0]]);
C=matrix([[1, 0, 0,0],[0, 1, 0,0],[0, 0, 1,0],[0, 0, 0,1]]);
D=matrix([[0],[0],[0],[0]]);
# Матрицы весовых коэффициентов
R=[[100]];
Q=matrix([[0.001, 0, 0,0],[0, 0.001, 0,0],[0, 0, 0.01,0],[0, 0,0,200]]);
# Синтез LQR-оптимального регулятора
(K,S,E)=lqr(A,B,Q,R)
# Вычисление составляющих функционала
N=A-B*K;
NN=N.T;
w=ss(N,B,C,D)
x0=matrix([[220], [147], [162],[0]]);
Ct=C.T;
P1=solve_lyapunov(NN,Ct*Q*C)
Kt=K.T;
x0t=x0.T;
Jx=abs((x0t*P1*x0)[0,0])
P2=solve_lyapunov(NN,Kt*R*K);
Ju=abs((x0t*P2*x0)[0,0])
fig = plt.figure(num=None, figsize=(9, 7), dpi=120, facecolor='w', edgecolor='k')
plt.suptitle('Переходные процессы в системе с оптимальным LQR ПИ-регулятором',size=14)
ax1 = fig.add_subplot(411)
y,x=step(w[0,0])
ax1.plot(x,y,"b")
plt.ylabel('out(1)')
ax1.grid(True)
ax2 = fig.add_subplot(412)
y,x=step(w[1,0])
ax2.plot(x,y,"b")
plt.ylabel('out(2)')
ax2.grid(True)
ax3 = fig.add_subplot(413)
y,x=step(w[2,0])
ax3.plot(x,y,"b")
plt.ylabel('out(3)')
ax3.grid(True)
ax4 = fig.add_subplot(414)
y,x=step(w[3,0])
ax4.plot(x,y,"b")
plt.ylabel('out(4)')
ax4.grid(True)
plt.xlabel('Время, с.')
plt.show()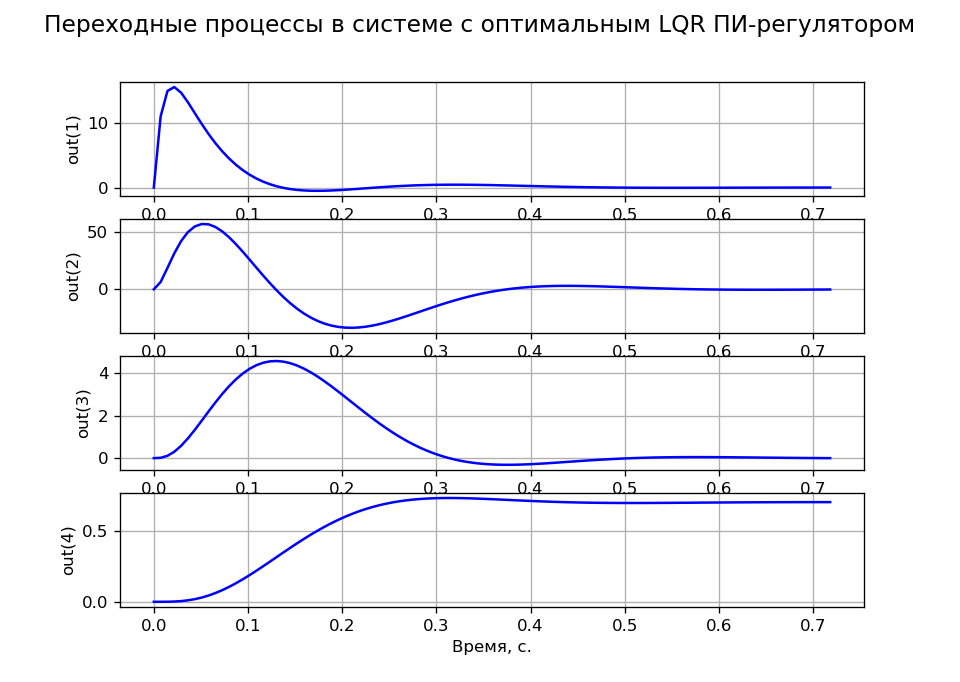
Рис. 4
Для определения матрицы К в библиотеке Python Control Systems Library есть две функции К=acker(A,B,s) и К = place (A,B,s), где s – вектор — строка желаемых полюсов передаточной функции замкнутой системы управления. Первая команда может быть использована только для систем с одним входом по u при n≤5. Вторая не имеет таких ограничений, однако кратность полюсов не должна превышать ранг матрицы В. Пример использования оператора acker() приведен в листинге и на (рис.5).
Листинг программы (рис.5).
# -*- coding: utf8 -*-
from numpy import*
from control.matlab import *
from matplotlib import pyplot as plt
i=(-1)**0.5
A=matrix([[-100,0,0],[143.678, -16.667,-195.402],[0,1.046,0]]);
B=matrix([[2300], [0], [0]]);
C=eye(3)
D=zeros([3,1])
p=[[-9.71+14.97*i -9.71-14.97*i -15.39 -99.72]];
k=acker(A,B,p)
H=A-B*k;
Wss=ss(H,B,C,D);
step(Wss)
w=tf(Wss)
fig = plt.figure()
plt.suptitle('Пример использования оператора acker()')
ax1 = fig.add_subplot(311)
y,x=step(w[0,0])
ax1.plot(x,y,"b")
ax1.grid(True)
ax2 = fig.add_subplot(312)
y,x=step(w[1,0])
ax2.plot(x,y,"b")
ax2.grid(True)
ax3 = fig.add_subplot(313)
y,x=step(w[2,0])
ax3.plot(x,y,"b")
ax3.grid(True)
plt.xlabel('Время, с.')
plt.show()
Рис. 5
Вывод
Приведенная в публикации реализация LQR- оптимизации электропривода с учётом использование новых lqr() и lyap() функций позволит при изучении соответствующего раздела теории управления отказаться от использования лицензионной программы MATLAB.
Пример LQR-оптимизации в летательном аппарате (ЛА)
(пример взят из публикации Astrom и Mruray, Глава 5 [8] и доработан автором статьи в части замены функции lqr() и приведения терминологии к общепринятой)Теоретическая часть, краткая теория, LQR оптимизации уже была рассмотрена выше, поэтому перейдём к анализу кода с соответствующими комментариями:
Необходимые библиотеки и функция LQR контролера.
from scipy.linalg import* #модули scipy для функции lqr
from numpy import * #модули numpy для алгебры матриц
from matplotlib.pyplot import * # модули для построения графиков
from control.matlab import * # функции control..ss() и control..step()
# Параметры модели и функция lqr()
m = 4; # масса ЛА в кг.
J = 0.0475; # момент инерции вращения вокруг оси тангажа в кг*и**2
#Танга́ж- это угловое движение ЛА относительно главной #горизонтальной оси инерции.
r = 0.25; # плечо силы тяги в м.
g = 9.8; # ускорение свободного падения в м/с**2
c = 0.05; # коэффициент демпфирования (расчетный)
def lqr(A,B,Q,R):
X =matrix(solve_continuous_are(A, B, Q, R))
K = matrix(inv(R)*(B.T*X))
E= eig(A-B*K)[0]
return X, K, E
Начальные условия и основные матрицы A,B,C,D модели.
xe = [0, 0, 0, 0, 0, 0];# начальное состояние x при равновесии (список)
ue = [0, m*g]; # вектор управления
# Динамическая матрица
A = matrix(
[[ 0, 0, 0, 1, 0, 0],
[ 0, 0, 0, 0, 1, 0],
[ 0, 0, 0, 0, 0, 1],
[ 0, 0, (-ue[0]*sin(xe[2]) - ue[1]*cos(xe[2]))/m, -c/m, 0, 0],
[ 0, 0, (ue[0]*cos(xe[2]) - ue[1]*sin(xe[2]))/m, 0, -c/m, 0],
[ 0, 0, 0, 0, 0, 0 ]])
# Входная матрица
B = matrix(
[[0, 0], [0, 0], [0, 0],
[cos(xe[2])/m, -sin(xe[2])/m],
[sin(xe[2])/m, cos(xe[2])/m],
[r/J, 0]])
# Выходная матрица
C = matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]])
D = matrix([[0, 0], [0, 0]])
Строим входы и выходы, соответствующие пошаговым изменениям в положении xy. Векторы xd и yd соответствуют желаемым установившимся состояниям в системе. Матрицы Cx и Cy являются соответствующими выходами модели. Для описания динамики системы используем систему векторно — матричных уравнений:
Динамику замкнутого контура можно смоделировать с помощью функции step(), для K\cdot xd и K\cdot xd в качестве входных векторов, где:
xd = matrix([[1], [0], [0], [0], [0], [0]]);
yd = matrix([[0], [1], [0], [0], [0], [0]]);
Текущая библиотека control 0.8.1 поддерживает только часть функций SISO Matlab по созданию контролеров обратной связи, поэтому для считывания данных с контролера, поэтому необходимо создать индексные вектора lat(),alt() для боковой -x и вертикальной — y динамики.
lat = (0,2,3,5);
alt = (1,4);
# Введение индексных векторов
Ax = (A[lat, :])[:, lat];
Bx = B[lat, 0];
Cx = C[0, lat];
Dx = D[0, 0];
Ay = (A[alt, :])[:, alt];
By = B[alt, 1]; Cy = C[1, alt]; Dy = D[1, 1];
# Использование диагональных матриц для определения K
Qx1 = diag([1, 1, 1, 1, 1, 1]);
Qu1a = diag([1, 1]);
X,K,E =lqr(A, B, Qx1, Qu1a)
K1a = matrix(K);
# Ввод единичного управления по координате x
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);
(Yx, Tx) = step(H1ax, T=linspace(0,10,100));
#Ввод единичного управления по координате y
H1ay = ss(Ay - By*K1a[1,alt], By*K1a[1,alt]*yd[alt,:], Cy, Dy);
(Yy, Ty) = step(H1ay, T=linspace(0,10,100));
Вывод графиков последовательно по одному для каждого задания.
figure();
title("Изменение на единицу x и y")
plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--');
plot([0, 10], [1, 1], 'k-');
axis([0, 10, -0.1, 1.4]);
ylabel('относительное перемещение');
xlabel('время');
legend(('x', 'y'), loc='lower right');
grid()
show()
График:
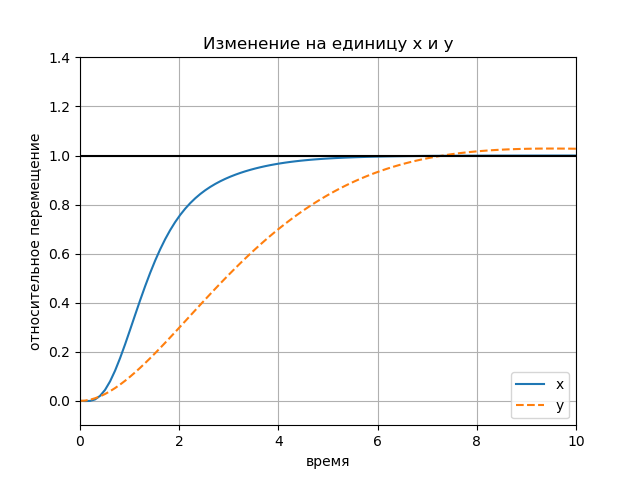
Влияние амплитуды входных воздействий
# Влияние амплитуды входных воздействий
Qu1a = diag([1, 1]);
X,K,E =lqr(A, B, Qx1, Qu1a)
K1a = matrix(K);
H1ax = ss(Ax - Bx*K1a[0,lat], Bx*K1a[0,lat]*xd[lat,:], Cx, Dx);
Qu1b = (40**2)*diag([1, 1]);
X,K,E =lqr(A, B, Qx1, Qu1b)
K1b = matrix(K);
H1bx = ss(Ax - Bx*K1b[0,lat], Bx*K1b[0,lat]*xd[lat,:],Cx, Dx);
Qu1c = (200**2)*diag([1, 1]);
X,K,E =lqr(A, B, Qx1, Qu1c)
K1c = matrix(K);
H1cx = ss(Ax - Bx*K1c[0,lat], Bx*K1c[0,lat]*xd[lat,:],Cx, Dx);
figure();
[Y1, T1] = step(H1ax, T=linspace(0,10,100));
[Y2, T2] = step(H1bx, T=linspace(0,10,100));
[Y3, T3] = step(H1cx, T=linspace(0,10,100));
plot(T1.T, Y1.T, 'r-');
plot(T2.T, Y2.T, 'b-');
plot(T3.T, Y3.T, 'g-');
plot([0 ,10], [1, 1], 'k-');
axis([0, 10, -0.1, 1.4]);
title("Влияние амплитуды входных воздействий")
legend(('1', '$1,6\cdot 10^{3}$','$4\cdot 10^{4}$'), loc='lower right');
text(5.3, 0.4, 'rho');
ylabel('относительное перемещение');
xlabel('время');
grid()
show()
График:

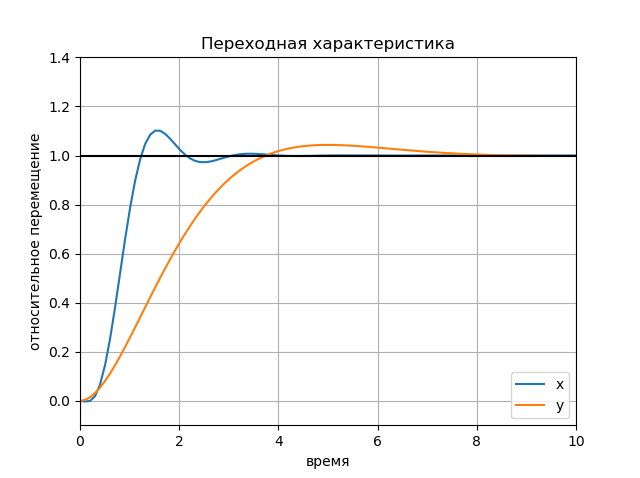
Переходная характеристика
# Изменение Qx влияет на выход
Qx2 = C.T * C;
Qu2 = 0.1 * diag([1, 1]);
X,K,E =lqr(A, B, Qx2, Qu2)
K2 = matrix(K);
H2x = ss(Ax - Bx*K2[0,lat], Bx*K2[0,lat]*xd[lat,:], Cx, Dx);
H2y = ss(Ay - By*K2[1,alt], By*K2[1,alt]*yd[alt,:], Cy, Dy);
figure();
[Y2x, T2x] = step(H2x, T=linspace(0,10,100));
[Y2y, T2y] = step(H2y, T=linspace(0,10,100));
plot(T2x.T, Y2x.T, T2y.T, Y2y.T)
plot([0, 10], [1, 1], 'k-');
axis([0, 10, -0.1, 1.4]);
title("Переходная характеристика")
ylabel('относительное перемещение');
xlabel('время');
legend(('x', 'y'), loc='lower right');
grid()
show()
График:
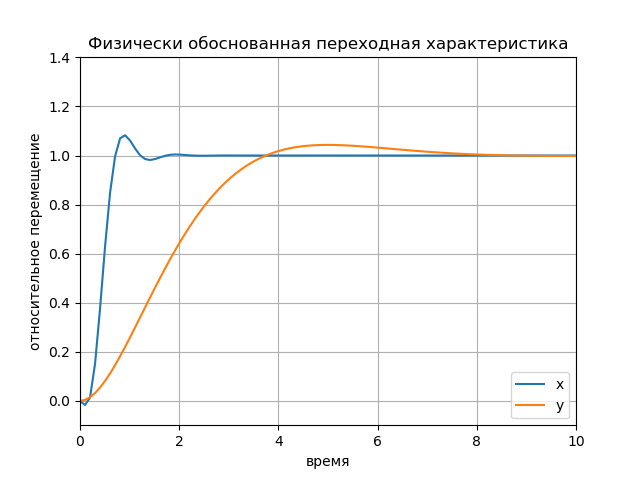
Физически обоснованная переходная характеристика
#Физически обоснованной переходная характеристика
# становиться при погрешностях измерений бокового перемещения
# не более 1 си. и вертикального не менее 10 см.
Qx3 = diag([100, 10, 2*pi/5, 0, 0, 0]);
Qu3 = 0.1 * diag([1, 10]);
X,K,E =lqr(A, B, Qx3, Qu3)
K3 = matrix(K);
H3x = ss(Ax - Bx*K3[0,lat], Bx*K3[0,lat]*xd[lat,:], Cx, Dx);
H3y = ss(Ay - By*K3[1,alt], By*K3[1,alt]*yd[alt,:], Cy, Dy);
figure();
[Y3x, T3x] = step(H3x, T=linspace(0,10,100));
[Y3y, T3y] = step(H3y, T=linspace(0,10,100));
plot(T3x.T, Y3x.T, T3y.T, Y3y.T)
axis([0, 10, -0.1, 1.4]);
title("Физически обоснованная переходная характеристика")
ylabel('относительное перемещение');
xlabel('время');
legend(('x', 'y'), loc='lower right');
grid()
show()
График:
Вывод:
Приведенная в публикации реализация LQR- оптимизации в ЛА с учётом использования новой lqr() функции позволит при изучении соответствующего раздела теории управления отказаться от использования лицензионной программы MATLAB.
Ссылки
1. Математика на пальцах: линейно-квадратичный регулятор.
2. Пространство состояний в задачах проектирования систем оптимального управления.
3. Использование библиотеки Python Control Systems Library для проектирования систем автоматического управления.
4. Python Control Systems Library.
5. Python — не может импортировать модуль slycot в spyder (RuntimeError & ImportError).
6. Python Control Systems Library.
7. Критерии оптимального управления и lqr-оптимизация в электроприводе.







