Комментарии 38
Да, Вы правы, я внес правку для прояснения этого момента

А в ЦОС подобное разделение так и вообще не имеет смысла — там что интерполяция, что экстраполяция равнозначны.
Кстати, есть еще Безье-интерполяция, которая не укладывается в данное определение интерполяции, ведь часть точек — управляющие.
Я понимаю, что кривую Безье в каждой точке можно вычислить с помощью последовательностей кусочно-линейных интерполяций и что в конце получится функция линейная по точкам и полиномиальная по параметру, но исходная задача не подпадает ни под определение интерполяции ни под определение кусочной интерполяции.
Никто не мешает интерполяцию использовать для экстраполяции:
Главное, чтобы был результат и понимание процесса. Поэтому автор поступил грамотно — дал определение терминов в начале.
Как весь этот матан в статье позволит перейти к аппроксимации комплексными синусоидами, например? Как он он поможет победить численную нестабильность в расчётах на большом количестве данных и полиномах степени выше 1?
Мне статья понравилась.
Если уж задаться вопросом, кому адресована эта статья, то это скорее читатель, который уже видел линейную регрессию, но знает её «только с одной стороны» (например, один раз делал на лабе по готовым формулам). Здесь же удалось собрать целый ряд разных подходов: с точки зрения матана, теорвера, линейки и т.д. Чем с большего числа сторон Вы взглянете на явление, тем глубже его поймете. Иногда задача решается удачным выбором точки зрения.
По поводу регрессии синусоидами, то процитирую себя же из статьи: «Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).» Берите синусы в качестве базисных функций и будут Вам синусы. Более того, гифка в разделе «произвольный базис» показывает регрессию в полиномиальном базисе.
По поводу нестабильности: это отдельная тема и здесь я лишь упомянул, что она существует. Охватить всё в одной статье невозможно, да и чтоб начать разбираться с нестабильностью, неплохо бы сначала разобраться в основах.
Берите синусы в качестве базисных функций и будут Вам синусыТо есть готовых, конкретных и пригодных к кодированию формул опять не будет. И не «синусы», а «комплексные синусоиды» — это не одно и то же. Если бы я на просьбу математика о программе для численных вычислений ответил «в учебнике [Страуструпа] всё написано, берите компилятор с++ и будет вам счастье» — вряд ли ему такой ответ понравился бы. И вряд ли бы он смог аналог матлаба наваять.
Я не уверен что такое "комплексная синусоида". Это exp(i x), где x — действительное число, а i — мнимая единица, или sin(Z), где Z комплексное, или Z sin(x), где x — действительное число, а Z — комплексное, или это что-то ещё? Сначала сформулируйте адекватно задачу: укажите что и на каком семействе функций Вы хотите "регрессировать" и тогда я смогу ответить, знаю ли я как такое решается и если да, то можно ли получить этот ответ из статьи. Кстати, если я расскажу про функции комплексного переменного, то будут претензии, что я ничего не написал про кватернионные синусы? Так нужно сразу написать про функции, действующие на любом линейном пространстве? Но ведь были претензии, что статья недостаточно элементарная. Теперь она уже недостаточно продвинутая?
Раз уже затронули комплексные числа, то на всякий случай прокомментирую их. Задача линейной регрессии совершенно "прямолинейно" обобщается и на комплексные числа. Если переписать всю статью в терминах комплексных чисел, то единственная заметная разница — вместо транспонированных матриц будут стоять эрмитово-сопряжённые, ну может ещё где-то появятся знаки сопряжения. Но приводить линейную регрессию для комплексных чисел я считаю излишеством: во-первых, это для понимания сложнее обычной регрессии (хотя формулы почти те же) и начинать с такого явно не стоит, во-вторых, это всё-таки довольно редкая задача — даже sklearn.LinearRegression выдаёт "Complex data not supported\n"
По поводу готовых формул для кодирования. Видите ли, уметь что-то запрограммировать по готовым формулам и понимать математический аппарат за ними — это два разных навыка. Эта статья ориентирована на развитие второго и для задачи "просто надо чтоб работало" будет малополезной. Но и так есть довольно много других хороших статей и лекций на ютубе, где рассматривается именно практическая часть, будь то самостоятельная имплементация регрессии или использование готовых библиотечных функций. А вот статей, которые показывают "математическое закулисье" мало, вот на эту нишу я и ориентировался.
Я не уверен что такое «комплексная синусоида». Это exp(i x), где x — действительное число, а i — мнимая единица, или sin(Z), где Z комплексное, или Z sin(x), где x — действительное число, а Z — комплексное, или это что-то ещё?Гугл даёт вполне однозначный ответ — хотя я предпочитаю более компактную запись в виде ix (наверняка её можно записать ещё более компактно с помощью статистических эстиматоров — только у меня не получилось). Конечно, можно рассмотреть действительную и мнимые компоненты по отдельности — но это лишает возможности контролировать амплитуду и фазу при аппроксимации.
Сначала сформулируйте адекватно задачуЗадачи типичные — шумоподавление квадратурного сигнала, аппроксимация спектра импульсной характеристики инвариантной к временной задержке, определение частоты.
Я не занимаюсь теорией обработки сигналов и могу не совсем понимать условие. Правильно ли я понимаю, что задача состоит, например, в следующем: для некоторой функции f, которая являет собой линейную комбинацию A_1 exp(i w_1 t) + A_2 exp(i w_2 t) +...+ A_2 exp(i w_N t) (сигнал) плюс случайная величина e (шум), необходимо найти A_1,...,A_N при известных w_1,...,w_n? Если да, то нужно воспользоваться разделом "Произвольный базис" и установить там базисные функции exp(i w_1 t),...,exp(i w_N t), а потом воспользоваться приведённой там формулой с учётом моего предыдущего комментария (транспонирование -> эрмитово сопряжение). Long story short, вот демонстрационный кусок кода для Mathematica
Remove["Global`*"]
basisF[t_] := {Exp[0.1*t*I], Exp[0.2*t*I], Exp[0.15*t*I]};
signalA = {5, 2, 3};
noiseA = 0.1/Sqrt[2];
sampleN = 100;
signal[t_] := signalA.basisF[t];
noise[t_] :=
noiseA*(RandomVariate[NormalDistribution[0, 1]] +
I*RandomVariate[NormalDistribution[0, 1]]);
Print["Signal to noise ratio = ", Norm[signalA]/noiseA]
(*Generate noisy signal*)
y = Table[N[signal[t] + noise[t]], {t, 0, sampleN}];
(*Construct features*)
\[CapitalPhi] = Table[N[basisF[t]], {t, 0, sampleN}];
(*Apply formula*)
w[y_, \[CapitalPhi]_] :=
Inverse[ConjugateTranspose[\[CapitalPhi]].\[CapitalPhi]].\
ConjugateTranspose[\[CapitalPhi]].y;
(*Result*)
recovered = Abs[w[y, \[CapitalPhi]]];
Print["Initial amplitudes:", signalA]
Print["Recovered amplitudes:", recovered]Signal to noise ratio = 87.178
Initial amplitudes:{5,2,3}
Recovered amplitudes:{5.00467,2.01432,2.99681}Ясно что при определённых условиях здесь могут быть проблемы, например кратные частоты при слишком малой частоте дискретизации могут привести к двум линейно зависимым столбцам матрицы. В статье эта проблема упоминается. Если это не та задача, что Вам интересна, то сформулируйте условие более понятно для неспециалиста в обработке сигналов.
a*Exp[k*t*I+phase]при аппроксимации которым ищется не только a, но и phase.
На самом деле, она там есть. w[y, [CapitalPhi]] — комплексное число и как у каждого уважающего себя комплексного числа у него есть и модуль Abs[w[y, [CapitalPhi]]], который я вывожу, и фаза, которую печатать не стал (всё равно в начальных условиях она везде ноль). Вот очень минималистичный пример с фазой
sampleN = 100;
signal[t_] =
5*Exp[0.1*t*I + 0.5*I] + 2*Exp[0.2*t*I + 0.8*I] +
3*Exp[0.15*t*I + 1.5*I];
noise[t_] :=
0.1*(RandomVariate[NormalDistribution[0, 1]] +
I*RandomVariate[NormalDistribution[0, 1]]);
y = Table[N[signal[t] + noise[t]], {t, 0, sampleN}];
\[CapitalPhi] = Table[N[basisF[t]], {t, 0, sampleN}];
w[y_, \[CapitalPhi]_] :=
Inverse[ConjugateTranspose[\[CapitalPhi]].\[CapitalPhi]].\
ConjugateTranspose[\[CapitalPhi]].y;
AbsArg[w[y, \[CapitalPhi]]]{{4.99847, 0.501885}, {1.9858, 0.802154}, {3.01153, 1.50344}}Раз уже затронули комплексные числа, то на всякий случай прокомментирую ихДавайте и я прокомментирую — всё, что может быть выражено через комплексные (и прочие) числа, должно через них и выражаться. Gimbal lock — наглядный пример ситуации, когда матричная алгебра заходит в тупик. Ещё наглядный пример — вот в этой статье вы можете сравнить решение автора традиционным подходом и решения через комплексные числа в комментариях.
1) Некоторые задачи естественно решаются с помощью одного аппарата, другие — с помощью другого. В частности, комплексные числа особенно хороши для двумерных задач, красиво решают задачи электротехники и т.п. При этом комплексные числа вовсе не исключают векторы, так например, при решении задачи движения нерелятивистской частицы со спином удобно объединить два комплексных числа в вектор.
Вообще, матрицы сами по себе, это просто таблицы с числами. Обычно эти числа — координаты чего-то (например тензора) в определенном базисе. Смысл в эти таблички вдыхает линейная алгебра (тензорный анализ).
2) Мне понравились Ваши комплексные гильоши ^^
3) Gimbal lock возникает не столько из-за матриц как таковых, сколько от неудачной параметризации (углы Эйлера). Можно выбрать другую параметризацию в матрицах или использовать единичные кватернионы. Кватернионы и правда удобны для представления вращений, но тоже не лишены проблем параметризации (двойное покрытие). Вообще, споры о том, что лучше — кватернионы или 3D векторы — восходит к Гиббсу и Гамильтону и мне тоже немного жалко, что сейчас кватернионы используются намного реже векторов.
Можно выбрать другую параметризацию в матрицах или использовать единичные кватернионыТак в этом-то и дело — чтобы описать через матрицы кватернионы, нужно заранее знать про кватернионы. Имея на руках матрицы поворота, полученные из комплексных чисел, нельзя получить из них матрицу для умножения кватернионов, просто увеличив размерность.
Также вычисления матрицами носит дискретный характер и посчитать производную или промежуточные значения будет непросто.
Также матрицы имеют очевидное ограничение на размерность. Оперировать бесконечными матрицами не получится ни в теории, ни на практике.
что лучше — кватернионы или 3D векторыЕсли поставить задачу о построении спирали, закрученной в спираль, закрученной в спираль (повторить n раз) и посчитать её длину, то ответ будет однозначным.
Также вычисления матрицами носит дискретный характер и посчитать производную или промежуточные значения будет непросто.
Вычисления с матрицами носят не более дискретный характер, чем с числами.
Если рассматривать матрицы фиксированного размера, то они образуют непрерывное многообразие. В тексте статьи я приводил ссылку на Matrix Cookbook. Там куча формул с дифференциированием и матриц и по матрицам, при чем многие одномерные тождества находят свои естественные матричные обобщения.
Также матрицы имеют очевидное ограничение на размерность. Оперировать бесконечными матрицами не получится ни в теории, ни на практике.
Бесконечномерные матрицы вполне себе использовались в вычислениях (например, матричная форма квантовой механики). Впрочем, насколько я понимаю, функциональный анализ предлагает более удачные альтернативы бесконечным матрицам.
Если поставить задачу о построении спирали, закрученной в спираль, закрученной в спираль (повторить n раз) и посчитать её длину, то ответ будет однозначным.
А Вы попробуйте с помощью кватернионов представить произвольное линейное преобразование и потом найти его собственные вектора и числа. Напишете условие для кватернионов, оно сведется к условиям на компоненты и придется решать систему линейных уравнений, которые удобно решать с помощью матриц.
Вы черри-пикаете задачи с вращением и утверждаете, что кватернионы/комплексные числа лучше. Для этих задач может и да, но область применения матриц огромна.
Окей, я понимаю что раньше матрицы сильно облегчали вычисления, но сейчас же у нас есть системы компьютерной алгебры! Когда мне нужно решить систему уравнений, я и вызываю метод с названием «решить систему уравнений», а СКА уже сама определяет, является ли она линейной, недо/переопределённой и т.д. Нет никакой необходимости заполнять матрицу вручную.
В программировании так и тем более — удобнее оперировать типами, а не реализацией. Понятно, что в памяти компьютера всё так или иначе хранится в тензорном виде, но всё-таки удобнее писать
Complex a;
Dual b;
Dual<Complex> c;а не
Matrix<2,1> complex_a;
Matrix<2,1> dual_b;
Matrix<2,2> dual_of_complex_c;чтобы при их умножении соответствующие матрицы автоматически выбирались в зависимости от типа.
Мне понравились Ваши комплексные гильоши ^^Спасибо)
Если вместо комплексных чисел взять кватернионы, то можно строить узоры на поверхности сферы. В статике они, правда, выглядят не особо интересно:



А делалось это не ради узоров, а ради синтеза звука.
гифка в разделе «произвольный базис» показывает регрессию в полиномиальном базисеЭта гифка сделана в стороннем инструменте используя метод под названием «полиномиальная регрессия», а вовсе не комбинацию статистических эстиматоров. Это не выглядит похожим на численную проверку ваших теоретических изысканий.
К сожалению, это не моё теоретическое изыскание, а вполне стандартный подход, преподаваемый во всех курсах ML. Вот, например, этот подход в известном курсе Воронцова http://www.machinelearning.ru/wiki/images/a/a2/Voron-ML-regression-slides.pdf (4-й слайд). На самом деле, я был бы искренне горд собой, будь это моим теоретическим изысканием.
По поводу стороннего инструмента, претензия мне совсем непонятна. С чего вдруг стало зазорно при иллюстрации подхода приводить примеры известных библиотек где он используется? И в выделеном куске кода как раз прекрасно видно, что "Полиномиальная регрессия" — это обычная линейная регрессия с базисом из полиномов (команда: make_pipeline(PolynomialFeatures(.), LinearRegression())). И даже можно догадаться, что PolynomialFeatures(.) строит нам строчки матрицы Phi (см. раздел перед гифкой). Или описание теории можно сопровождать исключительно своими велосипедами с квадратными колёсами? Или при упоминании третьесторонних библиотек ни в коем случае нельзя описывать на чём они базируются — преподавать как магию, а код как заклинания?
Отличная статья, спасибо! В университетском курсе всегда не хватало полноты картины, особенно когда на новом предмете пытались выдать регрессию за что то новое, не показывая связь с тем же самым тервером.
Я полагаю, под О(1) имеется в виду независимость от количества датапоинтов N, но не от размерности задачи n. В противном случае, я сомневаюсь в существовании подобных алгоритмов — результат работы регрессии составляют n чисел и независимый от размерности алгоритм не смог бы их даже распечатать "в один присест".
Если же достаточно независимости от N, то в некоторых разумных предположениях можно придумать подобный алгоритм, как раз основываясь на столь любимых Вами матрицах. Для этого обратимся к формуле раздела "Произвольный базис" и обратим внимание, что часть Phi^T y имеет размерность 1 х (n+1)

и всё остальное под минус первой степенью имеет размерность (n+1) х (n+1).

Основываясь на матричном умножении, легко доказать следующие два утверждения, проиллюстрированные графически


Строгих доказательств приводить не буду — любой видевший хоть обложку книги по матанализу должен уметь доказывать такое самостоятельно. Вместо этого приведу демонстрационный код
import numpy as np
# does regression
class Regressor:
def __init__(self, dimensions):
self.XTy = np.zeros(dimensions)
self.XTX = np.zeros((dimensions, dimensions))
def push_features(self, f, y):
self.XTy += f * y
self.XTX += f * f[np.newaxis].T
def get_regression_params(self):
return np.dot(np.linalg.inv(self.XTX), self.XTy)
# generates features from raw data
features = lambda x: np.concatenate(([1.0], x))
f = 10 # number of dimensions
r = Regressor(f + 1)
# create a dataset
N = 100 # numer of datapoints
np.random.seed(42)
X = np.random.rand(N, f)
Y = np.random.rand(N, 1) # should always be 1
# test regressor
for x,y in zip(X, Y):
r.push_features(features(x), y)
w = r.get_regression_params()
print('my:', w)
# do the same with scikit-learn
from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True) # Regressor fits with intersept
model.fit(X, Y)
print('sklearn:', model.intercept_, model.coef_)my: [ 0.50998109 0.04065423 -0.22417411 0.12527675 -0.01315162 0.06585738
0.05293676 0.06372162 -0.03954708 0.07962786 -0.05955656]
sklearn: [0.50998109] [[ 0.04065423 -0.22417411 0.12527675 -0.01315162 0.06585738 0.05293676
0.06372162 -0.03954708 0.07962786 -0.05955656]]Вся процедура происходит в классе Regressor. Он специально так спроектирован, чтоб подчёркивать независимость от количества датапоинтов N — их даже подавать туда надо по одной через push_features, потому что класс без понятия, сколько их будет. Вся память класса резервируется в конструкторе и больше никогда не увеличивается. С количеством датапоинтов я определяюсь уже после создания экземпляра класса. Не хотел усложнять код, но всё же написал сразу с генерацией фич features. Можно заказать r = Regressor(f) и подавать сырые иксы r.push_features(x, y), тогда результатом будет регрессия без свободного члена, эквивалент LinearRegression(fit_intercept=False).
По поводу сделанных предположений. Я полагаю, что выполняемые мной арифметические действия не приводят к переполнениям или большой потере точности. Ясно, что на практике это потребует дополниительного исследования и хотя бы "обвязки ифами", чтоб предупредить пользователя, что произошло переполнение или точность работы скомпрометирована.
avg += input[value]
avg -= delayed[value]вне зависимости от количества усредняемых данных.
Если памяти не хватает для хранения линии задержки — её можно организовать на внешнем устройстве, например, закольцованной магнитной ленте. В этом условии была подсказка на решение.
Для обеспечения устойчивости вычислений нужно использовать либо целочисленную арифметику, либо вводить обратную связь для компенсации накопленных погрешностей.
В разделе "Статистика" я пояснил откуда взялось такое название ("регрессия к среднему"). Вот кстати неплохое науч-поп видео про регрессию к среднему. Слово "редукция" тоже подходит, как по мне, но про dimension reduction обычно говорят в контексте метода главных компонент (PCA).
Насколько я понял, в статье рассмотрена регрессия (прогнозирование числовых значений) для бинарных тензоров. То есть для данных, которые можно выразить в матричном виде. Встречался ли автор с задачами регрессии значений полиарных тензоров (имеющих три и более измерений)?
Я конечно не уверена, но кажется там ошибка в формуле коэффициента b - лишний знак квадрата. Я выводила, и квадрата там не получилось, + опеределение дисперсии в этом месте вроде как предполагает просто квадрат мат ожидания.

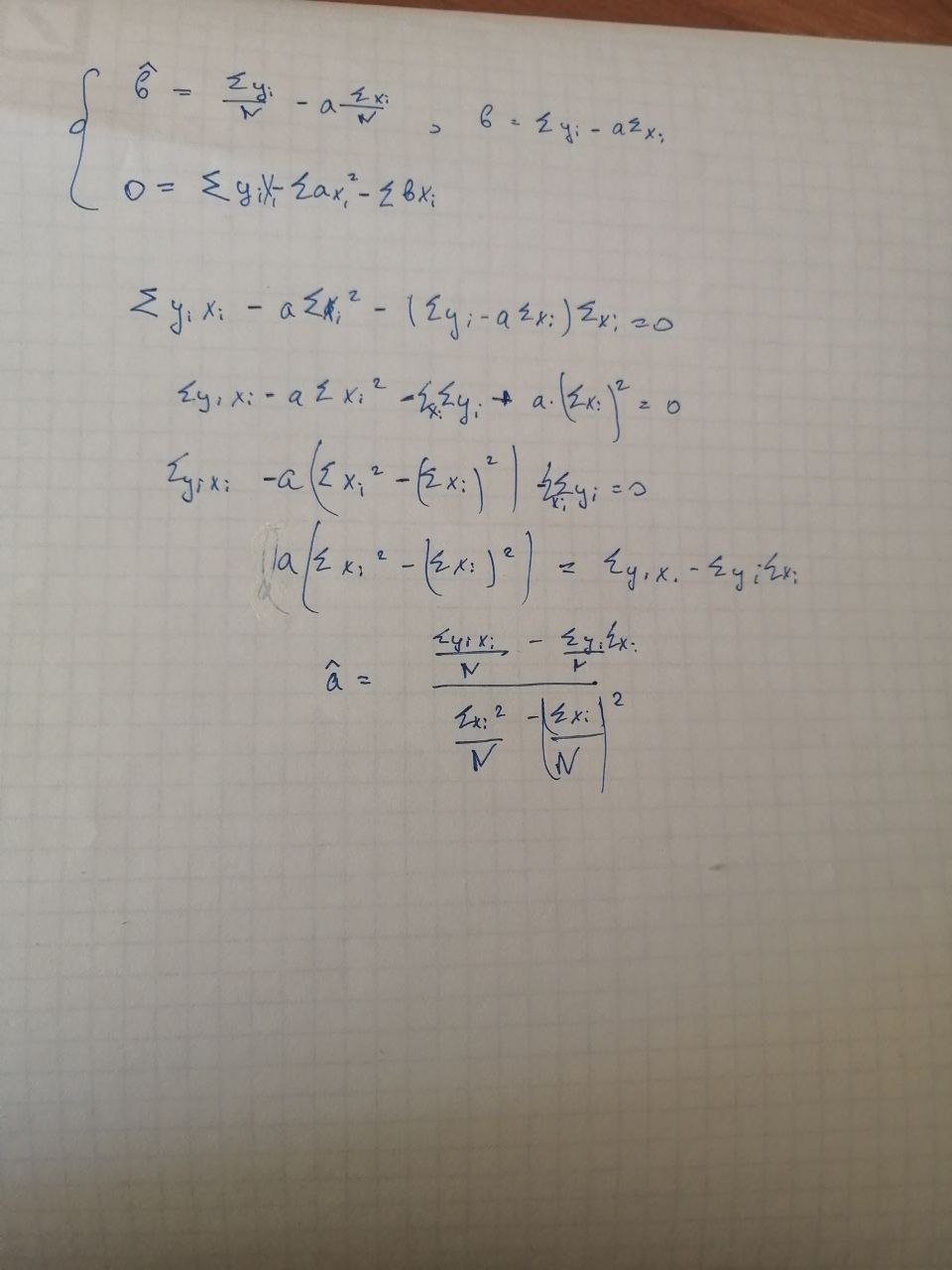
Спасибо за замечательную статью! Так намного лучше учить ML, чем "fit -> transpose" без понимания причинно-следственных связей "под капотом".

Основы линейной регрессии