Searching is the method to search for a specific element in a group of an element. It needs a unique identity that is associated with the desired element. As a unique identity of that desired element has been found, the index to that desired element is returned. The index indicates the location or address where that specific element has been found in the list elements of the array. If the desired data is found, particular data has been returned. Otherwise, it returned a null value.
There are several categories of search algorithms such as:
Linear search
Binary search
Interpolation search
Hash table search
A binary search algorithm is an approach for finding a position of a specified value within a sorted array. Binary search is the fastest and efficient searching technique used to find an element's position in a linear array.
Binary search can be applicable only on sorted arrays. For binary search, data should be sorted first, and it must be organized in either ascending order if the data is in the form of numbers or in alphabetical (A to Z) order if it is in strings format. To apply binary search at an array of data in an unsorted form, it must be sorted first using a sorting process in ascending order and then applying binary search.
In this technique, the array should be sorted first, and then the searching process is based on finding the midpoint by dividing the array into two halves. The essential purpose of binary search is to search the midpoint. If the desired element is not found on the first check, then the array is more divided into sub-arrays by repeating the same procedure. The binary search difficulty rises with more number elements in an array. Binary search is usually recognized as a logarithmic search or half interval search.
Working Principle of Binary Search
Its working principle is based on the "Divide and Conquer” rule. A divide and conquer method works by repetitively breaking down a problem into subproblems of a similar sort till these become meek sufficient to be solved straight.
Let's understand the working principle of binary search with the help of an example. The precondition for binary search is that the array should be sorted. If the data is not sorted, we can't apply binary search on that array. So let's understand the concept of binary search.
Firstly read the search element from the user as an input.
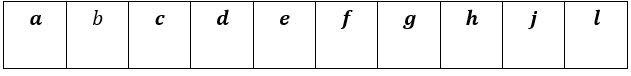
In this array, there are a total of 10 elements from 0 to 9 and arranged in ascending order.
The next step is to search the mid element in the sorted list of arrays. Now, we are going to find a mid-element of the array.
Because we want to find the mid-position of the array to divide it into two halves. For this purpose, let’s say the left value is 'a' and the right value is ‘l’. In the array. So, the formula will become like this:
Then comparison will be made between the search elements with the mid element in the sorted list. Suppose if 'x' is a searching element in the array, then there will be three cases.
Case 1:
If both elements are matched/found, then display "Given element is found” and end the function
Case 2:
If the desired search element is smaller than the mid element, then again perform the above procedure for the left sublist of the mid element.
Case 3:
If the desired search element is larger than the mid element, then again perform an above process for the right sublist of a mid element.
Further, a similar process will be repeated till we reach the desired search element. If the element also doesn't match the search element, then display "Element is not found in the list”.
Example
Let’s consider another example to understand the concept of binary search. We have taken the following array having elements from 0 to 9 as shown below:

Suppose if we have to search for 25. So the algorithm will check whether 25 exists in this array or not. If it exists in an array, then it has to return the index at which it was found. If it does not exist in that array, then it has to return -1. So, the first thing in a binary search algorithm is to define the range of elements to search. The leftmost position in the array is the starting index, and the rightmost position is the ending index. The next step is to look for the middle index. The index should be in integer form. So, we will take a floor value of 4.5, which is 4.In this way, the middle index will be 4.


The next step is to find the position of the searching element in the array concerning the middle. Now the middle element is 20. As searching element 25 is greater than 20. So, it will be present somewhere after 20. So we are only interested in elements to the right of the middle index. If A[Mid]< searching element, then search to the right of the middle element. Now search will start in this way, the starting index will be equal to Mid+1, and the end will remain the same.

Now, we again have to find the mid-index by following the same procedure as above.


The searching element that will be again checked is for the middle. In this case, the middle element is 50 at the 7th index position. So searching element 25 will come either left or right of the 50. As 25 is less than 50, so we will restrict our search to the left of 50. If the A[Mid]> searching element, then search to the left of the middle element. So, now the start will remain the same, and the end will be updated with Mid-1. Now the array will look like this.


We're searching for 25 in an array. And the middle element is also 25 at the 5th index position. And so we have found our searching element 25. And condition A[Mid]= searching element is fully filled.
Pseudo Code/Logic of Binary Search:
For that purpose, the binary Search function is used, which always stores numbers in integer format. In binary search function, there is a total of four parameters:
Int ar[ ]: It is an input array that contains input data in ascending order.
int x: It means left side element.
int y: It means right-side element.
Int z: It is a searching element.
If the left or zeroth element is less than or equal to the right (x<=y), it moves to the subsequent conditions. So, first, we need to find the mid element (x+y)/2, which will be stored in a mid variable whose data type is integer 'int'.If you need to search the particular element named 'z'. This specific element is compared with an array of mid "ar[Mid]".So, if ar[Mid] is precisely equal to z, it will return the middle element.
If the mid element is not matched with the searching element, it will go to the next condition. The next condition will be ar[Mid] > z, then find out the binary search algorithm on the left side. If the aforementioned conditions are false, it will move to the next condition that is ar[Mid]< z, and a binary search is performed. Finally, if the element is not present, then the return will be -1, which indicates the searching element is not in that particular list.
int bin_S( int ar[] , int x , int y, int z){
if (x <= y) {
int Mid = (x + y)/2;
if (ar[Mid] == z)
return Mid ;
if (ar[Mid] > z)
return bin_S(arr, x, Mid-1, z);
if (ar[Mid] < z)
return bin_S(arr, Mid+1, y, z);
}
return -1 ;
}Time Complexity Analysis
For time complexity analysis, we need to take the worst-case time. This worst-case depends on the size of the array. The worst-case scenario is that we keep dividing the array into halves and searching for the element. And finally, we will come to an element in the range of search for which we want to search. And we realize one element in our range is not equal to the element we are searching for in list elements, and we say that element is not found. So this is how the worst case of binary search works. So let’s find the time it would take. In binary search, we have to perform the comparison of the search element with the middle element. If the algorithm performs a minimum number of comparisons, then it would be the best case. And if the algorithm performs a maximum number of comparisons, then it would be the worst case. The time taken to complete a maximum number of comparisons will be less than the time taken to perform a minimum number of comparisons. The best case would occur when the search element is equal to the very first middle element of an array. The worst-case will arise when the search element is present at the beginning of the array list or end of the array. In binary search:
The worst case is "O(1)."
The best case is "O(log n)."
The average case is "O(log n)."
Binary Search Tree
Binary search in which for each node, the left child of that node is less than node, and the right child is greater than a node.
Left Child < Node
Right Child > Node
Binary search specialty lies in the fact that inorder traversal of this binary tree will result in sorted order of these elements. So, first, we must see the left subtree, then the right subtree of the binary search. Another essential property of a binary search tree is that it is easy to search for elements in the binary search tree. Therefore, we keep minimizing the range of searches using a binary search tree.
Binary Search Tree Pseudo Code
To understand pseudocode, let’s take an example in which we have to search for an element 5. First, we check whether the tree is empty or not. If the tree is empty, then the value will not be found. The binary Tree will be empty when there is no value at the root. So, in that case, the program will be returned null. Now in a case when a tree is not empty, we compare the searching element with the root. If the searching element is smaller than the root, then we must search in the left subtree. If the searching element is larger than the root, then we must search in the right subtree. If the searching element is equal to root, then it will return that element that has been found.

var v = "Value";
var r = "Root";
var n = null;
var l = "Left";
function search(v, r){
if(r==n){
return n;
}
if(r.data == v){
return r;
}
if(r.data > v){
return search(v, r.l);
}
if (r.data < v){
return search (v, r.r);
}
}Advantages and Disadvantages of Binary Search
Advantages:
We search elements in complete input in linear search, but in binary search, we eradicate half of the list.
It is one of the fastest searching algorithms.
Binary search is consistently implemented on the extensive list of data. It works much better as compared to linear search.
Disdvantages:
Binary search requires more memory or space in the computer.
It requires more cache memory for a random access operation.









