e1vanov 13 мая 2022 в 18:33

W-функция Ламберта и ее приложения

3 мин

13K

Python*Программирование*Алгоритмы*Математика*

Из песочницы

+25

Комментарии 14

KvanTTT 13 мая 2022 в 19:40

В детстве в школе "изобрел" тетрацию или гипероператор-4 (только потом узнал как это называется). И только когда вырос, узнал, что некоторые уравнения с тетрацией решаются с использованием W-функции ламберта. Самое простое:

x^x = x, x - ?
x = ln(k) / W(ln(k))

Так что эта функция вызывает у меня приятные ностальгические воспоминания :)

Вычисление W-функции Ламберта

Разве не более эффективней раскладывать в ряд Тейлора и не использовать ни логарифмы, ни рекурсию? https://en.wikipedia.org/wiki/Lambert_W_function#Asymptotic_expansions

Sdima1357 13 мая 2022 в 22:01

x^x=x для х не равного 0 имеем х^(х-1) = 1 , имеет два вполне очевидных корня +1 и -1 или я что-то путаю?

KvanTTT 13 мая 2022 в 22:10

Извините, опечатался. Имел в виду x ^ x = k, где k — константа. В решении написано правильно с k.

e1vanov 14 мая 2022 в 00:53

Доброй ночи! Я использую рекурсию и логарифмы при подсчете значений так называемой -1-ветви функции Ламберта, а разложение в ряд Тейлора дает значение 0-ветви в окрестности нуля

KvanTTT 14 мая 2022 в 13:56

Кстати, можно переписать функцию так, чтобы не использовать рекурсию, так эффективней, как-то так:

def LambertW_1(x):
    result = log(-x)
    for t in range(99):
        result = log(x / result)
    return result

e1vanov 15 мая 2022 в 09:23

Да, хороший вариант

KvanTTT 14 мая 2022 в 13:45

Если использовать тетрацию, то запись уравнения выглядела бы так: x^^2 = k.

alxndrlsn 15 мая 2022 в 09:20

любопытно... а меня с некоторых пор "тревожила" идея "мультипликата", в основе которой лежит предположение о том, что если для интегрируемой функции g(x) имеется ее первообразная G(x), то для функции f(x) представленной в виде экспоненты в степени g(x), тоже должна быть некая первообразная F(x) (и может даже только одна?), получаемая из f(x) некоторым преобразованием ("мультиплицированием"), которое соответствует интегрированию степени экспоненты (прошу прощения за невнятное пояснение, лучше взгляните на рисунок - осторожно! может быть заразно!):

M и ? - это и есть те недоступные моему пониманию функции

Может быть, кто-то тоже переболел такими "фантазиями" и разрешился от них?

R3EQ 13 авг 2022 в 23:03

В детстве в школе "изобрел" тетрацию или гипероператор-4

Я думаю, что каждый ученик, интересующийся математикой, "изобретал" гипероператоры. Неудивительно.

belch84 14 мая 2022 в 10:41

Можно подойти к решению уравнения

немного иначе.
Функция Ламберта является решением обыкновенного дифференциального уравнения (ОДУ)

Если доступно средство для численного решения дифференциальных уравнений, можно найти его решение, и вычислить корень по приведенной в публикации формуле

Конечно, численное решение дифференциального уравнения устроено намного сложнее, и при этом трудно достигнуть очень высокой точности, но при наличии готовой программы для решения ОДУ можно решить исходное уравнение совсем без программирования. Для уравнения

у меня получился корень 1.03215

Сравнение точного графика ф-ции Ламберта и решения дифференциального уравнения

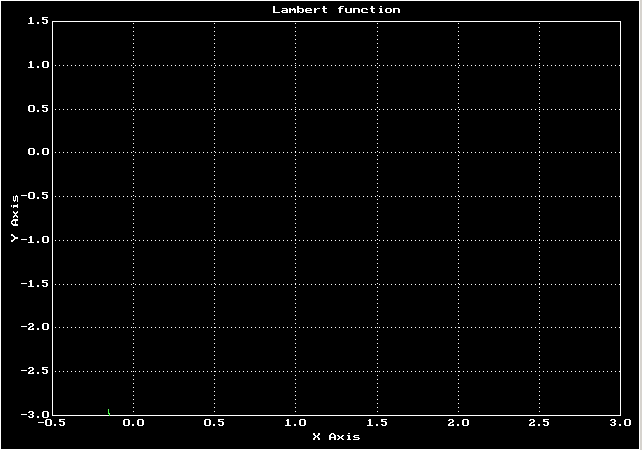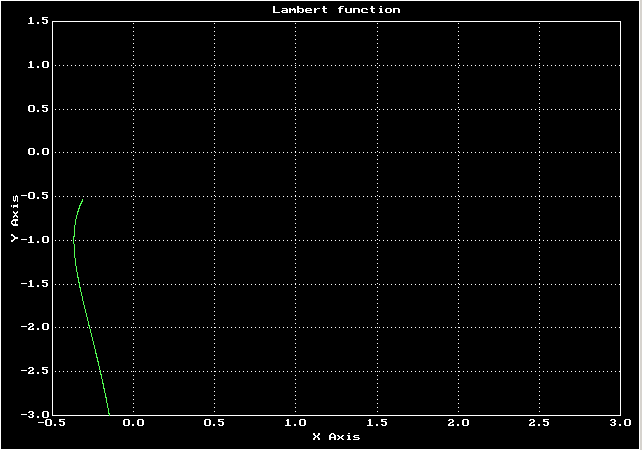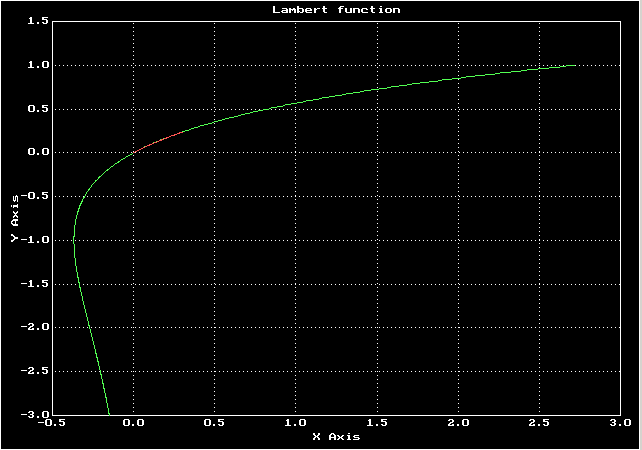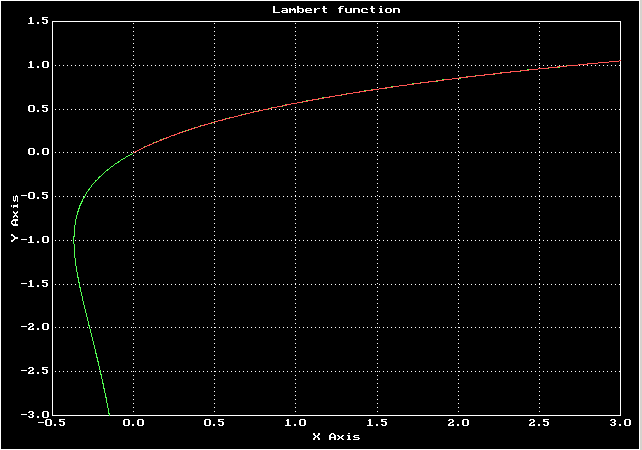
Зеленый — график функции Ламберта, красный — решение дифференциального уравнения

Un_ka 14 мая 2022 в 12:46

Графики были построены в GeoGebra?

e1vanov 14 мая 2022 в 20:09

В том числе. Еще использовались desmos и встроенное в macOS приложение "графический калькулятор"

yurixi 24 мая 2022 в 00:04

Есть такая функция, (1/(e^x-1)-1/x+1/2), она нечётная. Если заменить x на e^x и вычислить для получившейся g(x) интеграл int g(x) e^(sx) dx, то (с учётом, что интеграл чистой экспоненты вклада не даёт) нули будут совпадать с нетривиальными нулями дзета-функции. Если обозначить e^x = (-w)-1, то нули самой функции g(x) будут выполнять условие e^(-w)=e (-w), значит,
w e^w =-1/e. То есть, нули этой функции это все значения, включая комплексные, аналитического продолжения функции ламберта от -1/e.
Такие нули выполняют равенство e^e^x=1+e^x.
У функции g(x) есть и полюса, все решения e^e^x=1. Вместе полюса и нули определяют функцию, и параметризированный интеграл приводит к нетривиальным нулям дзета-функции. Можно сказать, что дзета-функция и функция ламберта не просто состоят в некоторой группе, они связаны напрямую.