Аннотация
В данной статье хочу рассказать как можно эффективно распараллелить алгоритм SSSP — поиска кратчайшего пути в графе с использованием графических ускорителей. В качестве графического ускорителя будет рассмотрена карта GTX Titan архитектуры Kepler.
Введение
В последнее время все большую роль играют графические ускорители (GPU) в не графических вычислениях. Потребность их использования обусловлена их относительно высокой производительностью и более низкой стоимостью. Как известно, на GPU хорошо решаются задачи на структурных сетках, где параллелизм так или иначе легко выделяется. Но есть задачи, которые требуют больших мощностей и используют неструктурные сетки. Примером такой задачи является Single Shortest Source Path problem (SSSP) – задача поиска кратчайших путей от заданной вершины до всех остальных во взвешенном графе. Для решения данной задачи на CPU существует, по крайней мере, два известных алгоритма: алгоритм Дейсктры и алгоритм Форда-Беллмана. Так же существуют параллельные реализации алгоритма Дейстры и Форда-Беллмана на GPU. Вот основные статьи, в которых описаны решения данной задачи:
- Accelerating Large Graph Algorithms on the GPU Using CUDA, Pawan Harish and P.J. Narayanan
- A New GPU-based Approach to the Shortest Path Problem, Hector Ortega-Arranz, Yuri Torres, Diego R. Llanos, and Arturo Gonzalez-Escribano
Есть и другие англоязычные статьи. Но во всех данных статьях используется один и тот же подход – идея алгоритма Дейсктры. Я опишу, как можно использовать идею алгоритма Форда-Беллмана и преимущества архитектуры Kepler для решения поставленной задачи. Об архитектуре GPU и об упомянутых алгоритмах уже много написано, поэтому в этой статье я не стану дополнительно писать про это. Так же, считается, что понятия варп(warp), cuda блок, SMX, и прочие базовые вещи, связанные с CUDA читателю знакомы.
Описание структуры данных
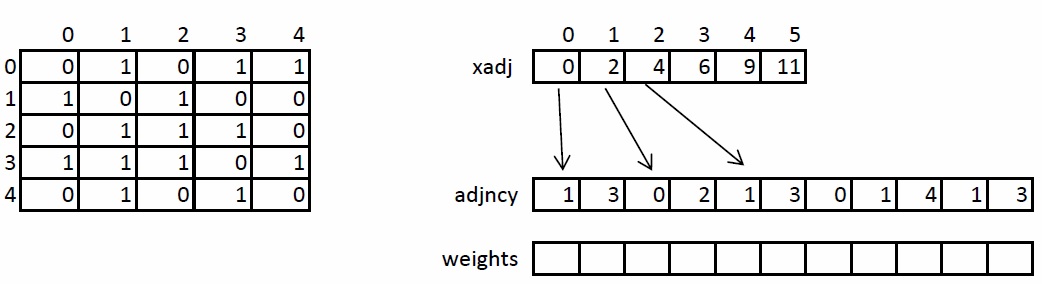
Кратко рассмотрим структуру хранения неориентированного взвешенного графа, так как в дальнейшем она будет упоминаться и преобразовываться. Граф задается в сжатом CSR формате. Данный формат широко распространен для хранения разреженных матриц и графов. Для графа с N вершинами и M ребрами необходимо три массива: xadj, adjncy, weights. Массив xadj размера N + 1, остальные два – 2*M, так как в неориентированном графе для любой пары вершин необходимо хранить прямую и обратную дуги.
Принцип хранения графа следующий. Весь список соседей вершины I находится в массиве adjncy с индекса xadj[I] до xadj[I+1], не включая его. По аналогичным индексам хранятся веса каждого ребра из вершины I. Для иллюстрации на рисунке слева показан граф из 5 вершин, записанный с помощью матрицы смежности, а справа – в CSR формате.
Реализация алгоритма на GPU
Подготовка входных данных
Для того чтобы увеличить вычислительную нагрузку на один потоковый мультипроцессор (SMX), необходимо преобразовать входные данные. Все преобразования можно разделить на два этапа:
- Расширение формата CSR в координатный формат (COO)
- Сортировка COO формата
На первом этапе необходимо расширить формат CSR следующим образом: введем еще один массива startV, в котором будем хранить начала дуг. Тогда в массиве adjncy будут храниться их концы. Таким образом, вместо хранения соседей, будем хранить дуги. Пример данного преобразования на графе, описанном выше:
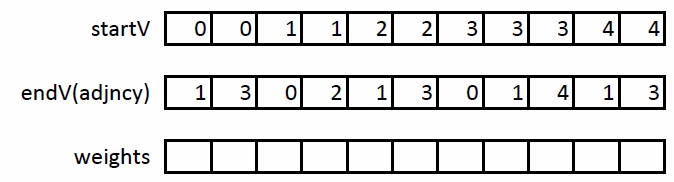
На втором этапе необходимо отсортировать полученные ребра так, чтобы каждая пара (U,V) встречалась ровно один раз. Таким образом, при обработке ребра (U,V) можно сразу обработать ребро (V,U), не считывая повторно данные об этом ребре из глобальной памяти GPU.
Основное вычислительное ядро
За основу для реализации на GPU взят алгоритм Форда-Беллмана. Данный алгоритм хорошо подходит для реализации на GPU в силу того, что ребра можно просматривать независимо друг от друга и данные ребер и их весов расположены подряд, что улучшает пропускную способность памяти GPU:int k = blockIdx.x * blockDim.x + threadIdx.x;
if(k < maxV)
{
double w = weights[k];
unsigned en = endV[k];
unsigned st = startV[k];
if(dist[st] > dist[en] + w) // (*)
{
dist[st] = dist[en] + w;
modif[0] = iter;
}
else if(dist[en] > dist[st] + w) // (**)
{
dist[en] = dist[st] + w;
modif[0] = iter;
}
}
В данном ядре, каждая нить обрабатывает два ребра (прямое и обратное), пытаясь улучшить расстояние по одному из них. Ясно, что оба условия if блока не могут выполниться одновременно. В отличие от алгоритма Форда-Беллмана, где каждое ребро просматривается последовательно, в реализованном на GPU алгоритме может возникнуть ситуация «гонки» потоков – когда два или более потока заходят обновить одну и ту же ячейку dist[I]. Покажем, что в данном случае алгоритм останется корректным.
Предположим, что есть две нити K1 и K2, которые хотят обновить ячейку dist[I]. Это означает, что выполнилось условие (*) или (**). Возможны два случая. Первый – одна из двух нитей записала наименьшее значение. Тогда на следующей итерации для этих двух нитей условие будет ложно, а значение в ячейке dist[I] окажется минимальным. Второй – одна из двух нитей записала не минимальное значение. Тогда на следующей итерации для одной из нитей условие будет истинно, а для другой – ложно. Тем самым, результат будет одинаковый в обоих случаях, но достигнут за разное количество итераций.
Согласно оптимизированному варианту алгоритма Форда-Беллмана, если на какой-либо итерации не было изменений в массиве dist, то дальше итерировать не имеет смысла. На GPU для этих целей была введена переменная modif, в которую нити записывали номер текущей итерации.
Одна итерация – один запуск ядра. В базовом варианте, на CPU в цикле запускаем ядро, далее считываем переменную modif и, если она не изменилась с предыдущей итерации, то в массиве dist ответ задачи – кратчайший путь из заданной вершины до всех остальных.
Оптимизация реализованного алгоритма
Далее рассмотрим некоторые оптимизации, которые позволяют существенно улучшить производительность алгоритма. Знание конечной архитектуры может быть полезным при выполнении оптимизаций.
Современные CPU имеют трехуровневый кэш. Размер кэша первого уровня равен 64КБ и содержится на всех вычислительных ядрах процессора. Размер кэша второго уровня варьируется от 1 до 2МБ. Кэш третьего уровня является общим для всего CPU и имеет размер порядка 12-15МБ.
Современные GPU имеют двухуровневый кэш. Размер кэша первого уровня равен 64КБ. Используется для разделяемой памяти и вытеснения регистров. Для разделяемой памяти доступно не более 48КБ. Содержится в каждом вычислительном блоке. Максимальный размер кэша второго уровня составляет 1,5МБ и является общим для всего GPU. Используется для кэширования данных, загружаемых из глобальной памяти GPU. В самом современном чипе GPU GK110 имеется 15 вычислительных блоков. Получается, что на один блок приходится примерно 48КБ кэша первого уровня и 102КБ кэша второго уровня. По сравнению с CPU, это очень мало, поэтому операции чтения из глобальной памяти графического процессора дороже, чем из оперативной памяти центрального процессора. Также в архитектуре Kepler появилась возможность прямого доступа в текстурный read-only кэш. Для этого необходимо добавить в ядре перед соответствующим формальным параметром const __restrict.
Использование текстурного кэша
В данной задаче требуется постоянно обновлять и считывать массив расстояний dist. Данный массив занимает достаточно мало места в глобальной памяти GPU по сравнению с информацией о дугах и их весах. Например, для графа с количеством вершин 220 (примерно 1 млн) массив dist будет занимать 8МБ. Несмотря на это, доступ к этому массиву осуществляется случайным образом, что плохо для GPU, так как порождаются дополнительные загрузки из глобальной памяти на каждый вычислительный варп. Для того чтобы минимизировать количество загрузок на один варп, необходимо сохранить данные в L2 кэше, прочитанные, но не использованные данные другими варпами.Так как текстурный кэш является read-only, то для того чтобы им воспользоваться пришлось ввести две разные ссылки на один и тот же массив расстояний dist. Соответствующий код:
__global__ void relax_ker (const double * __restrict dist, double *dist1, … …)
{
int k = blockIdx.x * blockDim.x + threadIdx.x + minV;
if(k < maxV)
{
double w = weights[k];
unsigned en = endV[k];
unsigned st = startV[k];
if(dist[st] > dist[en] + w)
{
dist1[st] = dist[en] + w;
modif[0] = iter;
}
else if(dist[en] > dist[st] + w)
{
dist1[en] = dist[st] + w;
modif[0] = iter;
}
}
}
В итоге получилось так, что внутри ядра все операции чтения ведутся с одним массивом, а все операции записи с другим. Но обе ссылки dist и dist1 указывают на один и тот же участок памяти GPU.
Локализация данных для лучшего использования кэша
Для лучшей работы описанной выше оптимизации необходимо, чтобы как можно дольше загруженные данные находились в L2 кэше. Доступ к массиву dist осуществляется по заранее известным индексам, хранящимся в массивах endV и startV. Для локализации обращений поделим массив dist на сегменты определенной длины, например, P элементов. Так как всего в графе N вершин, то получим (N / P + 1) разных сегментов. Далее, будем пересортировывать ребра в данные сегменты следующим образом. В первую группу отнесем ребра, концы которых попадают в нулевой сегмент, а начала – сначала в нулевой, затем в первый и т.д. Во вторую группу отнесем ребра, концы которых попадают в первый сегмент, а начала – сначала в нулевой, затем в первый и т.д.После данной перестановки ребер, значения элементов массива dist, соответствующие, например, первой группе будут находиться в кэше максимально долго, так как нити в первой группе будут запрашивать данные из нулевого сегмента для концевых вершин и нулевого, первого и т.д. для начальных вершин. Причем ребра расположены так, что нити будут запрашивать данные не более чем из трех различных сегментов.
Результаты тестирования алгоритма
Для тестирования использовались синтетические неориентированные RMAT-графы, которые хорошо моделируют реальные графы из социальных сетей и Интернета. Графы имеют среднюю связность 32, количество вершин является степень двойки. В таблице ниже приведены графы, на которых проводилось тестирование.| Количество вершин 2^N | Количество вершин | Количество дуг | Размер массива dist в МБ | Размер массивов ребер и весов в МБ |
| 14 | 16 384 | 524 288 | 0,125 | 4 |
| 15 | 32 768 | 1 048 576 | 0,250 | 8 |
| 16 | 65 536 | 2 097 152 | 0,500 | 16 |
| 17 | 131 072 | 4 194 304 | 1 | 32 |
| 18 | 262 144 | 8 388 608 | 2 | 64 |
| 19 | 524 288 | 16 777 216 | 4 | 128 |
| 20 | 1 048 576 | 33 554 432 | 8 | 256 |
| 21 | 2 097 152 | 67 108 864 | 16 | 512 |
| 22 | 4 194 304 | 134 217 728 | 32 | 1024 |
| 23 | 8 388 608 | 268 435 456 | 64 | 2048 |
| 24 | 16 777 216 | 536 870 912 | 128 | 4096 |
Из таблицы видно, что массив расстояний dist для графа с количеством вершин 218 и более не помещается целиком в L2 кэш на GPU. Тестирование производилось на GPU Nividia GTX Titan, у которого 14 SMX с 192 cuda ядрами (всего 2688) и на процессоре Intel core i7 3го поколения с частотой 3,4ГГц и 8МБ кэша. Для сравнения производительности на CPU использовался оптимизированный алгоритм Дейкстры. Никаких оптимизаций в виде перестановки данных перед работой на CPU не производились. Вместо времени показателем производительности будем считать количество дуг, обработанных за секунду времени. В данном случае, необходимо поделить полученное время на количество дуг в графе. В качестве конечного результата бралось среднее значение по 32 точкам. Также вычислялось максимальное и минимальное значения.
Для компиляции использовались компиляторы Intel 13й версии и NVCC CUDA 5.5 с флагами –O3 –arch=sm_35.
В качестве результата проделанной работы рассмотрим следующий график:

На данном графике изображены кривые средней производительности для следующих алгоритмов:
- cache && restrict on — алгоритм GPU со всеми оптимизациями
- cache off — алгоритм GPU без оптимизации перестановок для улучшенного кэширования
- restrict off — алгоритм GPU без оптимизации текстурного кэша
- cache && restrict off — базовый алгоритм GPU без оптимизаций
- CPU — базовый алгоритм на CPU
Видно, что обе оптимизации сильно влияют на производительность. Стоит отметить, что неверное использование оптимизации const __restrict может ухудшить производительность. Полученное ускорение можно увидеть на данном графике:
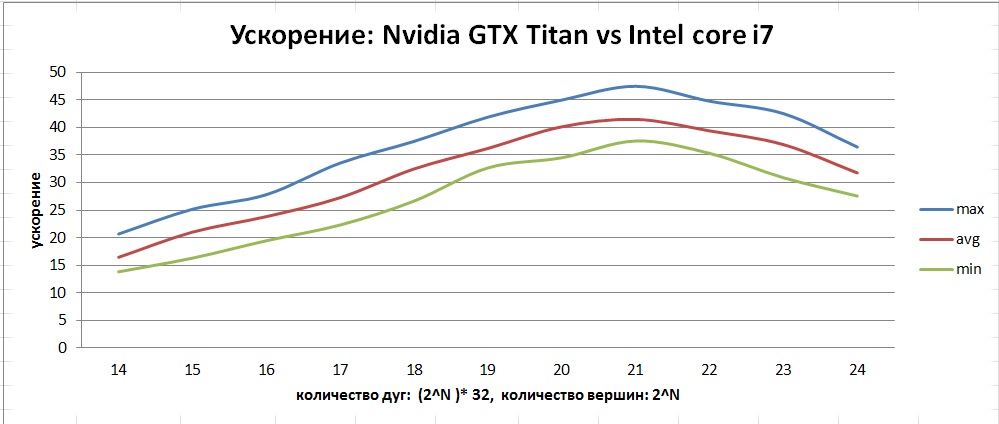
По приведенному графику видно, что в отличие от CPU, на GPU наблюдается бОльший диапазон отклонений от среднего. Это связано с особенностью реализации алгоритма в виде «гонки» потоков, так как от запуска к запуску можем получить разное количество итераций.
Заключение
В результате проделанной работы был разработан, реализован и оптимизирован алгоритм SSSP — поиска кратчайших путей в графе. Данный алгоритм ищет кратчайшие расстояния в графе от заданной вершины до всех остальных. Среди всех графов, которые поместились в память GTX Titan максимальную производительность показывают графы с количеством вершин до 221 — порядка 1100 млн ребер в секунду. Максимальное среднее ускорение, которое удалось достичь — порядка 40 на графах с количеством вершин от 1 до 4 млн.