Если вас интересует, как помочь обездвиженному человеку управлять компьютером для общения с внешним миром – вам сюда. Если вам интересно, какое отношение к этому имеют мел-частотные кепстральные коэффициенты и нейронные сети – вам тоже сюда.
Часть I. Программа для управления компьютером при помощи голоса
Ко мне обратился человек с просьбой написать программу, которая позволила бы управлять компьютерной мышью при помощи голоса. Тогда я и представить себе не мог, что, практически полностью парализованный человек, который даже не может сам повернуть голову, а может лишь разговаривать, способен развить бурную деятельность, помогая себе и другим жить активной жизнью, получать новые знания и навыки, работать и зарабатывать, общаться с другими людьми по всему свету, участвовать в конкурсе социальных проектов.
Позволю себе привести здесь пару ссылок на сайты, автором и/или идейным вдохновителем которых является этот человек – Александр Макарчук из города Борисов, Беларусь:
 |
«У Совы» — школа дистанционного обучения для людей с ограниченными возможностями. sova.by |
 |
«Без ограничений» — советы для тех, кому нужно работать на компьютере без рук bezogranicheniy.ru |
Для работы на компьютере Александр использовал программу «Vocal Joystick» — разработку студентов Университета штата Вашингтон, выполненную на деньги Национального Научного Фонда (NSF). См. melodi.ee.washington.edu/vj
Не удержался
Кстати, на сайте университета (http://www.washington.edu/) 90% статей именно про деньги. Трудно найти что-нибудь про научную работу. Вот, например, выдержки с первой страницы: «Том, выпускник университета, раньше питался грибами и с трудом платил за квартиру. Теперь он старший менеджер ИТ-компании и кредитует университет», «Большие Данные помогают бездомным», «Компания обязалась заплатить 5 миллионов долларов за новый учебный корпус».
Это одному мне режет глаз?
Это одному мне режет глаз?
Программа была сделана в 2005-2009 годах и хорошо работала на Windows XP. В более свежих версиях Windows программа может зависнуть, что неприемлемо для человека, который не может встать со стула и её перезапустить. Поэтому программу нужно было переделать.
Исходных текстов нет, есть только отдельные публикации, приоткрывающие технологии, на которых она основана (MFCC, MLP – читайте об этом во второй части).
По образу и подобию была написана новая программа (месяца за три).
Собственно, посмотреть, как она работает, можно здесь:
Скачать программу и/или посмотреть исходные коды можно здесь.
Никаких особенных действий для установки программы выполнять не надо, просто щёлкаете на ней, да запускаете. Единственное, в некоторых случаях требуется, чтобы она была запущена от имени администратора (например, при работе с виртуальной клавиатурой “Comfort Keys Pro”):

Пожалуй, стоит упомянуть здесь и о других вещах, которые я ранее делал для того, чтобы можно было управлять компьютером без рук.
Если у вас есть возможность поворачивать голову, то хорошей альтернативой eViacam может послужить гироскоп, крепящийся к голове. Вы получите быстрое и точное позиционирование курсора и независимость от освещения.
Подробнее – здесь.
Если вы можете двигать только зрачками глаз, то можно использовать трекер направления взгляда и программу к нему (могут быть сложности, если вы носите очки).
Подробнее – здесь.
Часть II. Как это устроено?
Из опубликованных материалов о программе «Vocal Joystick» было известно, что работает она следующим образом:
- Нарезка звукового потока на кадры по 25 миллисекунд с перехлёстом по 10 миллисекунд
- Получение 13 кепстральных коэффициентов (MFCC) для каждого кадра
- Проверка того, что произносится один из 6 запомненных звуков (4 гласных и 2 согласных) при помощи многослойного персептрона (MLP)
- Воплощение найденных звуков в движение/щелчки мыши
Первая задача примечательна лишь тем, что для её решения в реальном времени пришлось вводить в программу три дополнительных потока, так как считывание данных с микрофона, обработка звука, проигрывание звука через звуковую карту происходят асинхронно.
Последняя задача просто реализуется при помощи функции SendInput.
Наибольший же интерес, мне кажется, представляют вторая и третья задачи. Итак.
Задача №2. Получение 13 кепстральных коэффициентов
Если кто не в теме – основная проблема узнавания звуков компьютером заключается в следующем: трудно сравнить два звука, так как две непохожие по очертанию звуковые волны могут звучать похоже с точки зрения человеческого восприятия.
И среди тех, кто занимается распознаванием речи, идёт поиск «философского камня» — набора признаков, которые бы однозначно классифицировали звуковую волну.
Из тех признаков, что доступны широкой публике и описаны в учебниках, наибольшее распространение получили так называемые мел-частотные кепстральные коэффициенты (MFCC).
История их такова, что изначально они предназначались совсем для другого, а именно, для подавления эха в сигнале (познавательную статью на эту тему написали уважаемые Оппенгейм и Шафер, да пребудет радость в домах этих благородных мужей. См. A. V. Oppenheim and R.W. Schafer, “From Frequency to Quefrency: A History of the Cepstrum”).
Но человек устроен так, что он склонен использовать то, что ему лучше знакомо. И тем, кто занимался речевыми сигналами, пришло в голову использовать уже готовое компактное представление сигнала в виде MFCC. Оказалось, что, в общем, работает. (Один мой знакомый, специалист по вентиляционным системам, когда я его спросил, как бы сделать дачную беседку, предложил использовать вентиляционные короба. Просто потому, что их он знал лучше других строительных материалов).
Являются ли MFCC хорошим классификатором для звуков? Я бы не сказал. Один и тот же звук, произнесённый мною в разные микрофоны, попадает в разные области пространства MFCC-коэффициентов, а идеальный классификатор нарисовал бы их рядом. Поэтому, в частности, при смене микрофона вы должны заново обучать программу.
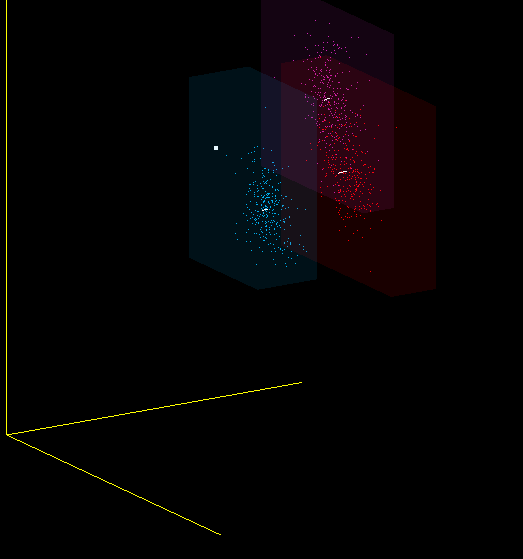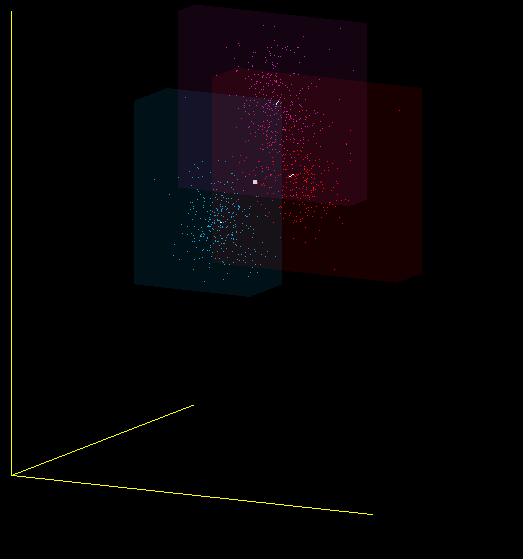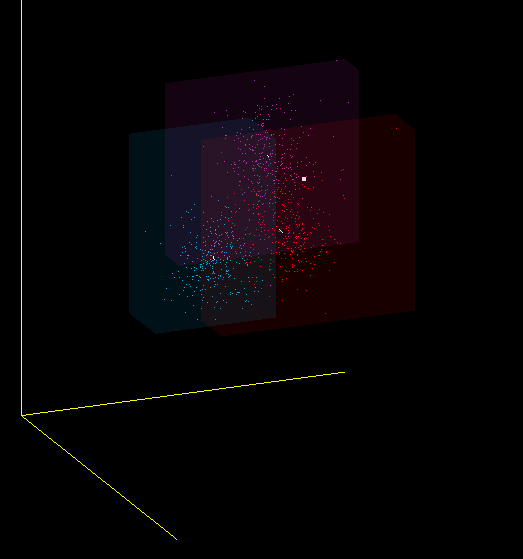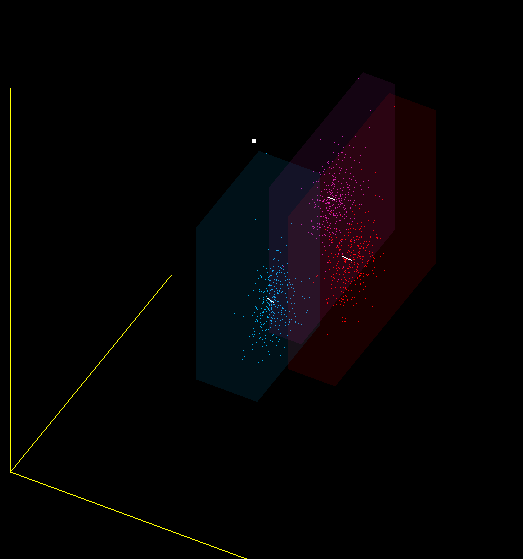
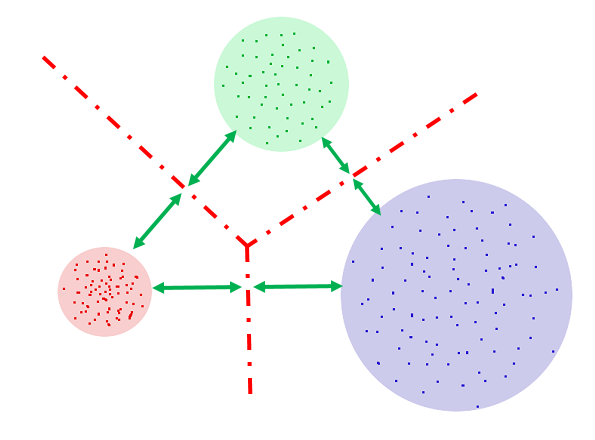
Это всего лишь одна из проекций 13-мерного пространства MFCC в 3-мерное, но и на ней видно, что я имею в виду – красные, фиолетовые и синие точки получены от разных микрофонов: (Plantronix, встроенный массив микрофонов, Jabra), но звук произносился один.
Однако, поскольку ничего лучшего я предложить не могу, также воспользуюсь стандартной методикой – вычислением MFCC-коэффициентов.
Чтобы не ошибиться в реализации, в первых версиях программы в качестве основы был использован код из хорошо известной программы CMU Sphinx, точнее, её реализации на языке C, именующейся pocketsphinx, разработанной в Университете Карнеги-Меллона (мир с ними обоими! (с) Хоттабыч).
Исходные коды pocketsphinx открыты, да вот незадача – если вы их используете, то должны в своей программе (как в исходниках, так и в исполняемом модуле) прописать текст, содержащий, в том числе, следующее:
* This work was supported in part by funding from the Defense Advanced
* Research Projects Agency and the National Science Foundation of the
* United States of America, and the CMU Sphinx Speech Consortium.Мне это показалось неприемлемым, и пришлось код переписать. Это сказалось на быстродействии программы (в лучшую сторону, кстати, хотя «читабельность» кода несколько пострадала). Во многом благодаря использованию библиотек “Intel Performance Primitives”, но и сам кое-что оптимизировал, вроде MEL-фильтра. Тем не менее, проверка на тестовых данных показала, что получаемые MFCC-коэффициенты полностью аналогичны тем, что получаются при помощи, например, утилиты sphinx_fe.
В программах sphinxbase вычисление MFCC-коэффициентов производится следующими шагами:
| Шаг | Функция sphinxbase | Суть операции |
|---|---|---|
| 1 | fe_pre_emphasis | Из текущего отсчёта вычитается большая часть предыдущего отсчета (например, 0.97 от его значения). Примитивный фильтр, отбрасывающий нижние частоты. |
| 2 | fe_hamming_window | Окно Хемминга – вносит затухание в начале и конце кадра |
| 3 | fe_fft_real | Быстрое преобразование Фурье |
| 4 | fe_spec2magnitude | Из обычного спектра получаем спектр мощности, теряя фазу |
| 5 | fe_mel_spec | Группируем частоты спектра [например, 256 штук] в 40 кучек, используя MEL-шкалу и весовые коэффициенты |
| 6 | fe_mel_cep | Берём логарифм и применяем DCT2-преобразование к 40 значениям из предыдущего шага. Оставляем первые 13 значений результата. Есть несколько вариантов DCT2 (HTK, legacy, классический), отличающихся константой, на которую мы делим полученные коэффициенты, и особой константой для нулевого коэффициента. Можно выбрать любой вариант, сути это не изменит. |
В эти шаги ещё вклиниваются функции, которые позволяют отделить сигнал от шума и от тишины, типа fe_track_snr, fe_vad_hangover, но нам они не нужны, и отвлекаться на них не будем.
Были выполнены следующие замены для шагов по получению MFCC-коэффициентов:
| Шаг | Функция sphinxbase | Переделка |
|---|---|---|
| 1 | fe_pre_emphasis | cas_pre_emphasis (через frame[i] -= frame[i — 1] * pre_emphasis_alpha;) |
| 2 | fe_hamming_window | for(i=0;i<MM_SOUND_BUFFER_LEN;i++) buf_in[i]*=(0.53836-0.46164*cos(2*3.14159*i/(MM_SOUND_BUFFER_LEN-1))); |
| 3 | fe_fft_real | ippsDFTFwd_RToCCS_32f |
| 4 | fe_spec2magnitude | for(i=0;i<=DFT_SIZE/2;i++) buf_ipp[i]=buf_ipp[i*2]*buf_ipp[i*2]+buf_ipp[i*2+1]*buf_ipp[i*2+1]; |
| 5 | fe_mel_spec | cas_mel_spec (через предрасчитанную таблицу) |
| 6 | fe_mel_cep | CS_mel_cep (через логарифм + ippsDCTFwd_32f_I) |
Что же дальше? У нас есть вектор 13-мерного пространства. Как определить, к какому звуку он относится?
Задача №3. Проверка того, что произносится один из 6 запомненных звуков
В программе-оригинале «Vocal Joystick» для классификации использовался многослойный персептрон (MLP) – нейронная сеть без новомодных наворотов.
Давайте посмотрим, насколько оправдано применение нейронной сети здесь.
Вспомним, что делают нейроны в искусственных нейронных сетях.
Если у нейрона N входов, то нейрон делит N-мерное пространство пополам. Рубит гиперплоскостью наотмашь. При этом в одной половине пространства он срабатывает (выдаёт положительный ответ), а в другой – не срабатывает.
Давайте посмотрим на [практически] самый простой вариант – нейрон с двумя входами. Он, естественно, будет делить пополам двумерное пространство.
Пусть на вход подаются значения X1 и X2, которые нейрон умножает на весовые коэффициенты W1 и W2, и добавляет свободный член C.
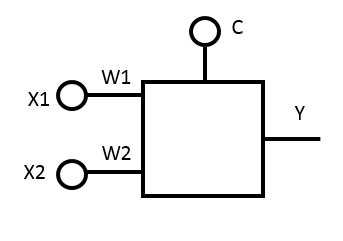
Итого, на выходе нейрона (обозначим его за Y) получаем:
Y=X1*W1+X2*W2+C
(опустим пока тонкости про сигмоидальные функции)
Считаем, что нейрон срабатывает, когда Y>0. Прямая, заданная уравнением 0=X1*W1+X2*W2+C как раз и делит пространство на часть, где Y>0, и часть, где Y<0.
Проиллюстрируем сказанное конкретными числами.
Пусть W1=1, W2=1, C=-5;
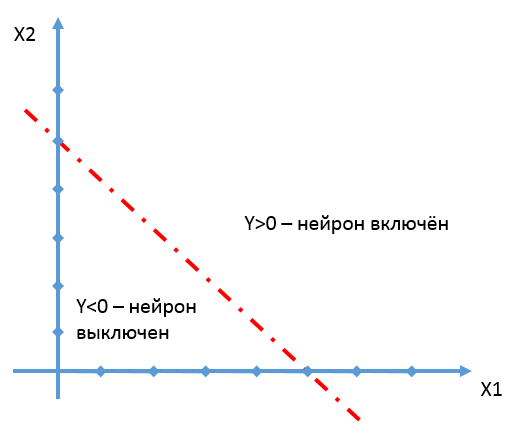
Теперь посмотрим, как нам организовать нейронную сеть, которая бы срабатывала на некоторой области пространства, условно говоря – пятне, и не срабатывала во всех остальных местах.
Из рисунка видно, что для того, чтобы очертить область в двумерном пространстве, нам потребуется по меньшей мере 3 прямых, то есть 3 связанных с ними нейрона.

Эти три нейрона мы объединим вместе при помощи ещё одного слоя, получив многослойную нейронную сеть (MLP).

А если нам нужно, чтобы нейронная сеть срабатывала в двух областях пространства, то потребуется ещё минимум три нейрона (4,5,6 на рисунках):

И тут уж без третьего слоя не обойтись:

А третий слой – это уже почти Deep Learning…

Теперь обратимся за помощью к ещё одному примеру. Пусть наша нейронная сеть должна выдавать положительный ответ на красных точках, и отрицательный – на синих точках.

Если бы меня попросили отрезать прямыми красное от синего, то я бы сделал это как-то так:

Но нейронная сеть априори не знает, сколько прямых (нейронов) ей понадобится. Этот параметр надо задать перед обучением сети. И делает это человек на основе… интуиции или проб и ошибок.
Если мы выберем слишком мало нейронов в первом слое (три, например), то можем получить вот такую нарезку, которая будет давать много ошибок (ошибочная область заштрихована):

Но даже если число нейронов достаточно, в результате тренировки сеть может «не сойтись», то есть достигнуть некоторого стабильного состояния, далёкого от оптимального, когда процент ошибок будет высок. Как вот здесь, верхняя перекладина улеглась на два горба и никуда с них не уйдёт. А под ней большая область, порождающая ошибки:

Снова, возможность таких случаев зависит от начальных условий обучения и последовательности обучения, то есть от случайных факторов:
— Что ты думаешь, доедет то колесо, если б случилось, в Москву или не доедет?
— А ты как думаешь, сойдётся ента нейронная сеть или не сойдётся?
Есть ещё один неприятный момент, связанный с нейронными сетями. Их «забывчивость».
Если начать скармливать сети только синие точки, и перестать скармливать красные, то она может спокойно отхватить себе кусок красной области, переместив туда свои границы:

Если у нейронных сетей столько недостатков, и человек может провести границы гораздо эффективнее нейронной сети, зачем же их тогда вообще использовать?
А есть одна маленькая, но очень существенная деталь.
Я очень хорошо могу отделить красное сердечко от синего фона отрезками прямых в двумерном пространстве.
Я неплохо смогу отделить плоскостями статую Венеры от окружающего её трёхмерного пространства.
Но в четырёхмерном пространстве я не смогу ничего, извините. А в 13-мерном — тем более.
А вот для нейронной сети размерность пространства препятствием не является. Я посмеивался над ней в пространствах малой размерности, но стоило выйти за пределы обыденного, как она меня легко уделала.
Тем не менее вопрос пока открыт – насколько оправдано применение нейронной сети в данной конкретной задаче, учитывая перечисленные выше недостатки нейронных сетей.
Забудем на секунду, что наши MFCC-коэффициенты находятся в 13-мерном пространстве, и представим, что они двумерные, то есть точки на плоскости. Как в этом случае можно было бы отделить один звук от другого?
Пусть MFCC-точки звука 1 имеют среднеквадратическое отклонение R1, что [грубо] означает, что точки, не слишком далеко отклоняющиеся от среднего, наиболее характерные точки, находятся внутри круга с радиусом R1. Точно так же точки, которым мы доверяем у звука 2 находятся внутри круга с радиусом R2.

Внимание, вопрос: где провести прямую, которая лучше всего отделяла бы звук 1 от звука 2?
Напрашивается ответ: посередине между границами кругов. Возражения есть? Возражений нет.
Исправление: В программе эта граница делит отрезок, соединяющий центры кругов в соотношении R1:R2, так правильнее.
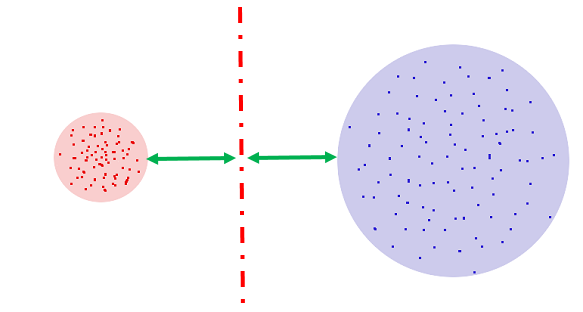
Далее, представим, что звука три. В этом случае проведём границы между каждой парой звуков.
И, наконец, не забудем, что где-то в пространстве есть точка, которая является представлением полной тишины в MFCC-пространстве. Нет, это не 13 нулей, как могло бы показаться. Это одна точка, у которой не может быть среднеквадратического отклонения. И прямые, которыми мы отрежем её от наших трёх звуков, можно провести прямо по границам окружностей:

На рисунке ниже каждому звуку соответствует кусок пространства своего цвета, и мы можем всегда сказать, к какому звуку относится та или иная точка пространства (или не относится ни к какому):

Ну, хорошо, а теперь вспомним, что пространство 13-мерное, и то, что было хорошо рисовать на бумаге, теперь оказывается тем, что не укладывается в человеческом мозгу.
Так, да не так. К счастью, в пространстве любой размерности остаются такие понятия, как точка, прямая, [гипер]плоскость, [гипер]сфера.
Мы повторяем все те же действия и в 13-мерном пространстве: находим дисперсию, определяем радиусы [гипер]сфер, соединяем их центры прямой, рубим её [гипер]плоскостью в точке, равно отдалённой от границ [гипер]сфер.
Никакая нейронная сеть не сможет более правильно отделить один звук от другого.
Здесь, правда, следует сделать оговорку. Всё это справедливо, если информация о звуке – это облако точек, отклоняющихся от среднего одинаково во всех направлениях, то есть хорошо вписывающееся в гиперсферу. Если бы это облако было фигурой сложной формы, например, 13-мерной изогнутой сосиской, то все приведённые выше рассуждения были бы не верны. И возможно, при правильном обучении, нейронная сеть смогла бы показать здесь свои сильные стороны.
Но я бы не рисковал. А применил бы, например, наборы нормальных распределений (GMM), (что, кстати и сделано в CMU Sphinx). Всегда приятнее, когда ты понимаешь, какой конкретно алгоритм привёл к получению результата. А не как в нейронной сети: Оракул, на основе своего многочасового варения бульона из данных для тренировки, повелевает вам принять решение, что запрашиваемый звук – это звук №3. (Меня особенно напрягает, когда нейронной сети пытаются доверить управление автомобилем. Как потом в нестандартной ситуации понять, из-за чего машина повернула влево, а не вправо? Всемогущий Нейрон повелел?).
Но наборы нормальных распределений – это уже отдельная большая тема, которая выходит за рамки этой статьи.
Надеюсь, что статья была полезной, и/или заставила ваши мозговые извилины поскрипеть.