Здесь даже можно будет замоделировать трансформатор и операционный усилитель, но все по порядку.
Электрические цепи можно описать следующими уравнениями:
(Напряжение падения на катушке равно минус ЭДС)
В механике есть следующие уравнения:
(Внешняя сила, действующая на пружину равна минус силе состороны пружины, если в точке приложение силы нет массы)
Как вы наверно догадались, электрические и механические величины можно сопоставить двумя способами:
Обычно, когда пытаются провести электро-механическую аналогию, используют первый способ, хотя кое-где можно встретить и второй, им-то мы и воспользуемся.
Но мы будем моделировать во вращательной механике, где каждую поступательную величину мы заменим соответствующим моментом или угловой величиной:
Но для простоты обозначать будем как в поступательной механике:
Так как в электричестве есть понятия потенциал (в точке) и напряжение (между точками), потенциал мы будем моделировать скоростью вращения вала, а напряжение — разностью скоростей двух валов. Ее можно получить при помощи дифференциала (как в автомобиле), у которого один из боковых валов инвертирован:

Выше были изложены пространные теоретические рассуждения, почему мы будем делать именно так. Дальше будет непосредственно описано, как мы это будем делать.
Можно моделировать как вал, вращающийся с постоянной скоростью (который ну ни как невозможно остановить), и подключенный к разностному входу дифференциала. С двух других его концов можно снимать напряжение (они крутятся друг относительно друга с постоянной скоростью).
То же самое, но только используется вал, выдающий постоянный крутящий момент. Такой вал без нагрузки будет разгонятся до бесконечно большой скорости вращения.
От дифференциала идут лопасти и опускаются в стакан с жидкостью.
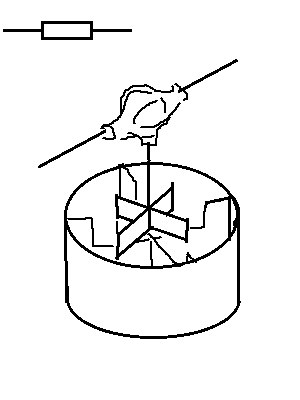
Чем более вязкая жидкость — тем больше проводимость, тем меньше сопротивление. Между несоединенными валами бесконечное сопротивление. А у резистора, у которого заклинило лопасти — сопротивление нулевое. Можно пофантазировать о напряжении пробоя, и трении между валом и его держателями, но по моему это сходство как-то не очень.

Так же как и в идеальном конденсаторе нет тока утечки, также и в его модели совсем нет трения. Так же как сила тока заряжает конденсатор, так же момент сил между валами разгоняет маховик. В таком конденсаторе на одной пластине всегда заряд , а на другой –
, а на другой –  .
.
Также емкостью может обладать одиночная сфера (или проводник другой формы). Если он заряжен зарядом Q, то на его поверхности будет потенциал . Их отношение и будет емкостью этого проводника. Это можно замоделировать маховиком без дифференциала.
. Их отношение и будет емкостью этого проводника. Это можно замоделировать маховиком без дифференциала.


(«Заземлением» будем обозначать неподвижные части конструкции)
Где v — разность скоростей двух валов, а x — их относительное смещение.
Если считать, что жесткость пружинки достаточно велика, а момент сил, передаваемый из одного вала в другой, достаточно мал, то катушку можно замоделировать так:

Если пофантазировать, то можно провести аналогию между петлей гистерезиса ферромагнетиков и неупругой деформацией пружинки. Правда в ферромагнетиках нет аналога усталости металла.
А также, модель катушки можно использовать как модель амперметра, если присоединить стрелку к выходу дифференциала.
Ее направление отклонения от положения равновесия будет свидетельствовать о том, в какую сторону вал №1 толкает вал №2. А ее величина — о моменте сил, с которым один вал воздействует на другой, т.е. о силе тока через моделируемую катушку.
И из казалось бы самого простого закона получается, что минус [ЭДС катушки] = [напряжению падения на ней] = разности скоростей валов = производной по времени относительного смещения двух валов. В катушке, которая ни к чему не подключена всегда ток =0, а в ее модели пружина не деформирована. Но если в катушке есть ток, а потом ее накоротко замкнуть (сверхпроводником), то ток в ней так и останется, а ее модель так и будет оставаться в деформированном состоянии.
получается, что минус [ЭДС катушки] = [напряжению падения на ней] = разности скоростей валов = производной по времени относительного смещения двух валов. В катушке, которая ни к чему не подключена всегда ток =0, а в ее модели пружина не деформирована. Но если в катушке есть ток, а потом ее накоротко замкнуть (сверхпроводником), то ток в ней так и останется, а ее модель так и будет оставаться в деформированном состоянии.
В принципе в катушке можно обойтись без дифференциала, но в трансформаторе, который содержит в себе пару катушек, так уже не получится.


Изначально конденсатор не заряжен.
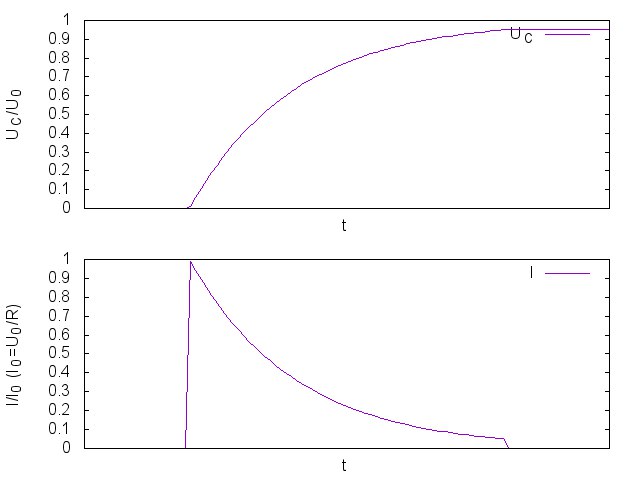
Включаем ключ (после этого ), и на резисторе оказывается напряжение питания, через него начинает течь ток и заряжать конденсатор, что эквивалентно тому, что на конденсаторе начинает расти напряжение, а на резисторе соответственно падать, и ток соответственно тоже начинает падать. Если через некоторое время ключ разомкнуть, то конденсатор так и останется заряженным, а напряжение на резисторе упадет до 0.
), и на резисторе оказывается напряжение питания, через него начинает течь ток и заряжать конденсатор, что эквивалентно тому, что на конденсаторе начинает расти напряжение, а на резисторе соответственно падать, и ток соответственно тоже начинает падать. Если через некоторое время ключ разомкнуть, то конденсатор так и останется заряженным, а напряжение на резисторе упадет до 0.
Изначально маховик покоится.
Включаем ключ (после этого сумма скоростей маховика и лопастей резистора равна скорости источника напряжения), маховик в начальный момент покоится, а лопасти резистора (невесомые) начинают вращаться, но из-за трения возникает момент сил, который разгоняет маховик. Чем быстрее крутится маховик, тем медленнее крутятся лопасти резистора, и тем с меньшей силой вращают маховик. Если через некоторое время ключ разомкнуть, то маховик продолжит вращаться не меняя своей скорости, а скорость лопастей резистора упадет до 0.

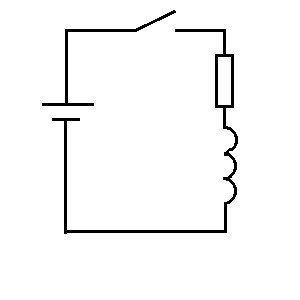
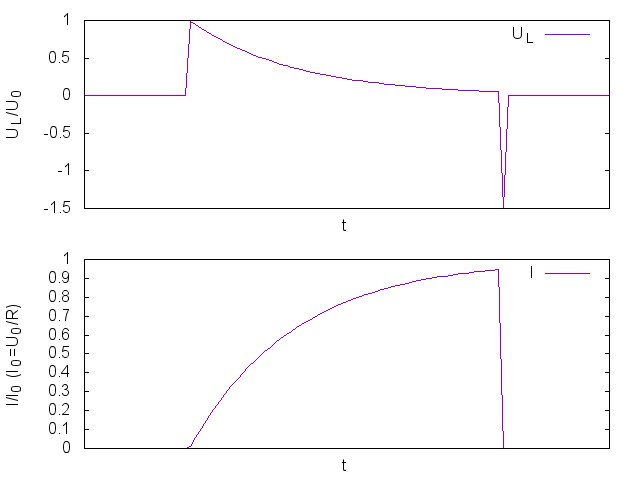
Вначале ток равен нулю. Мы включаем ключ (после этого ), и на катушку подается напряжение питания, и оно начинает постепенно разгонять ток через катушку. По мере увеличения тока, увеличивается напряжение падения на резисторе, а значит напряжение, разгоняющее ток в катушке, падает, а значит ток постепенно перестает расти. Если через некоторое время ключ разомкнуть, то в результате практически мгновенной остановки тока на катушке будет очень короткий всплеск ЭДС, полярность которого будет обратна полярности источника напряжения.
), и на катушку подается напряжение питания, и оно начинает постепенно разгонять ток через катушку. По мере увеличения тока, увеличивается напряжение падения на резисторе, а значит напряжение, разгоняющее ток в катушке, падает, а значит ток постепенно перестает расти. Если через некоторое время ключ разомкнуть, то в результате практически мгновенной остановки тока на катушке будет очень короткий всплеск ЭДС, полярность которого будет обратна полярности источника напряжения.
Вначале пружинка не растянута. Мы включаем ключ (после этого сумма скоростей деформации пружинки и лопастей резистора равна скорости источника напряжения), и пружинка начинает растягиваться так, как будто в самый начальный момент сопротивление резистора =0. Уже растянутая пружинка начинает оказывать силу на резистор, в результате чего в резисторе возникает разность скоростей, а в пружинке разность скоростей начинает уменьшаться. Чем больше пружинка натянута, тем большую силу она оказывает на резистор, тем больше разность скоростей в резисторе, и тем меньше разность скоростей в катушке (вернее в ее модели), и тем медленнее растягивается пружинка катушки дальше. Если через некоторое время ключ разомкнуть, то в результате практически мгновенного падения нагрузки на пружинку, она очень быстро сожмется в исходное положение.
Механическую модель можно упростить, представив себе покоящуюся на воде невесомую лодку, к которой прикреплена пружинка, а другой конец пружинки внезапно начинают тянуть с постоянной скоростью. Вначале лодка покоится. Потом пружинка начинает натягиваться, и чем больше натягивается, тем больше увлекает за собой лодку, и тем меньше разность между скоростями двух концов пружинки. А если пружинку отпустить (масса кораблика и масса пружинки =0), то кораблик тут же остановится, а пружинка тут же сожмется.
Сам трансформатор описывается также как катушка:

где
Иначе говоря трансформатор описывается системой уравнений:
%0A)
И чтобы получить механическую модель трансформатора, достаточно взять механические модели двух катушек, и соединить их пружинкой через рычаг:
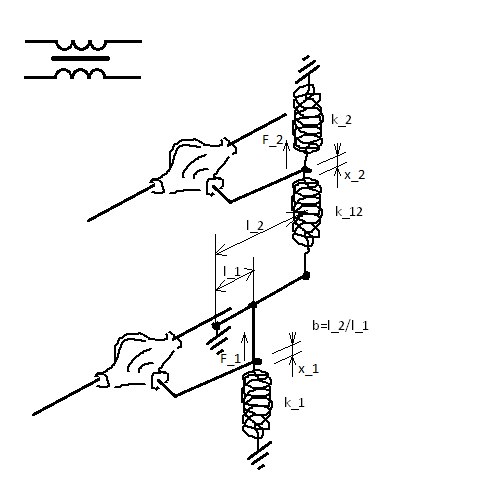
Можно все поступательные пружинки заменить на вращательные, а рычаг заменить на редуктор:

Найдем уравнения, описывающие эту систему.
Предположим, что нижнее плечо сместилось вверх на (в месте крепления пружины) под действием силы
(в месте крепления пружины) под действием силы  , а верхнее сместилось вверх на
, а верхнее сместилось вверх на  (в месте крепления пружины) под действием силы
(в месте крепления пружины) под действием силы  . Записав вторые законы Ньютона для обоих невесомых плеч, идущих от дифференциалов, получим систему:
. Записав вторые законы Ньютона для обоих невесомых плеч, идущих от дифференциалов, получим систему:
%5C%5C%0AF_2%3Dk_2%20x_2%2Bk_%7B12%7D(x_2-bx_1)%0A%5Cend%7Bcases%7D%0A)
что тоже самое с
x_1-bk_%7B12%7Dx_2%5C%5C%0AF_2%3D-bk_%7B12%7Dx_1%2B(k_2%2Bk_%7B12%7D)x_2%0A%5Cend%7Bcases%7D%0A)
ее можно разрешить относительно и
и  :
:

где))
Сравнивая эту систему с (1) получается, что матрицу

следует сопоставлять с матрицей
%7D%0A)
И если у нас есть трансформатор, у которого все витки одинаковые по форме и сечению, на 1й обмотке витков, на второй —
витков, на второй —  , и
, и  — доля от магнитного потока, создаваемого 1й катушкой, которая проходит через 2ю катушку (или наоборот — они совпадают) (Если катушки находятся на большом расстоянии, то
— доля от магнитного потока, создаваемого 1й катушкой, которая проходит через 2ю катушку (или наоборот — они совпадают) (Если катушки находятся на большом расстоянии, то  и это фактически две разные катушки. А если катушки близко друг к другу и к тому же соединены сердечником, то
и это фактически две разные катушки. А если катушки близко друг к другу и к тому же соединены сердечником, то  .), то матрица индуктивностей будет выглядеть так:
.), то матрица индуктивностей будет выглядеть так:

где — коэффициент, зависящий от размеров трансформатора и материала сердечника.
— коэффициент, зависящий от размеров трансформатора и материала сердечника.
Если в его модели взять , то из соотношений
, то из соотношений

отношения жесткостей пружин будут выглядеть так:
)


а матрица индуктивностей модели так:
![[L] =
\begin{pmatrix}
(k_2+k_{12})/b^2 & k_{12}/b \\
k_{12}/b & k_2+k_{12}
\end{pmatrix}
\frac{1}{k_2^2+2k_{12}k_2}](https://tex.s2cms.ru/svg/%5BL%5D%20%3D%20%0A%5Cbegin%7Bpmatrix%7D%0A(k_2%2Bk_%7B12%7D)%2Fb%5E2%20%20%20%20%26%20k_%7B12%7D%2Fb%20%20%5C%5C%0Ak_%7B12%7D%2Fb%20%20%20%20%20%20%20%20%26%20k_2%2Bk_%7B12%7D%20%20%20%20%0A%5Cend%7Bpmatrix%7D%0A%5Cfrac%7B1%7D%7Bk_2%5E2%2B2k_%7B12%7Dk_2%7D%0A)
т.к.![c \in [0..1]](https://tex.s2cms.ru/svg/c%20%5Cin%20%5B0..1%5D) , то
, то  =>
=> 
то соотношения жесткостей тоже >0 (если исключить из модели рычаг, т.е. b=1, то одно из этих соотношений окажется отрицательным, а пружин с отрицательной жесткостью не бывает).
И обратно: при любых соотношения жесткостей пружин


и при любом соотношении плеч рычага b>0
![c=\frac{1}{\sqrt{1+a_1/b^2 +a_2+a_1a_2/b^2}} \in [0..1]](https://tex.s2cms.ru/svg/c%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B1%2Ba_1%2Fb%5E2%20%2Ba_2%2Ba_1a_2%2Fb%5E2%7D%7D%20%5Cin%20%5B0..1%5D)
%20%3D%20(1%2Ba_2)%2Fb)
%20%3D%20(1%2Bb%5E2a_1)%2Fb)
При
 и модели катушек становятся практически независимыми.
и модели катушек становятся практически независимыми.
При
 и модели катушек становятся жестко соединены через рычаг без пружинки. А индуктивности начинают стремится к
и модели катушек становятся жестко соединены через рычаг без пружинки. А индуктивности начинают стремится к
![[L_{11}]=\frac{k_2+k_{12}}{b^2(k_2^2+2k_{12}k_2)}\to \frac{1}{2b^2k_2}=\frac{1}{2k_1}](https://tex.s2cms.ru/svg/%5BL_%7B11%7D%5D%3D%5Cfrac%7Bk_2%2Bk_%7B12%7D%7D%7Bb%5E2(k_2%5E2%2B2k_%7B12%7Dk_2)%7D%5Cto%20%5Cfrac%7B1%7D%7B2b%5E2k_2%7D%3D%5Cfrac%7B1%7D%7B2k_1%7D)
![[L]\to
\frac{1}{2}
\begin{pmatrix}
1/k_1 & 1/bk_2\\
1/bk_2 & 1/k_2
\end{pmatrix}](https://tex.s2cms.ru/svg/%5BL%5D%5Cto%0A%5Cfrac%7B1%7D%7B2%7D%0A%5Cbegin%7Bpmatrix%7D%0A1%2Fk_1%20%20%20%26%201%2Fbk_2%5C%5C%0A1%2Fbk_2%20%20%26%201%2Fk_2%0A%5Cend%7Bpmatrix%7D%0A)

и рассчитаем ее

->

пусть

%7D%0A)
тогда

последнее уравнение можно переписать в виде

OPOC:
%7D%3E0)
Этот вклад будет виден только сразу после включения схемы, потом затухнет и не будет участвовать в установившемся режиме трансформации.
Если изменить уравнение так:

и искать ЧРНС в виде , то придем к алгебраическому уравнению
, то придем к алгебраическому уравнению

=>
%5E2%7D%7D)
%20%3D%20%5Cfrac%7B%5Comega%7D%7BM_%7B22%7DR_2%7D)
т.к. , то
, то
%5E2%7D%7D%0A%5Ccos(%5Comega%20t-arctg%20%5Cfrac%7B%5Comega%7D%7BM_%7B22%7DR_2%7D)%3D)
![=\frac{-cU_0}{\sqrt{\omega^2\frac{N_1^2N_2^2}{L_0}(1-c^2)+\frac{N_1^2}{N_2^2}R_2^2}}\cos(\omega t-arctg\frac{\omega N_2^2(1-c^2)L_0}{R_2})\xrightarrow[c\to 1]{}](https://tex.s2cms.ru/svg/%3D%5Cfrac%7B-cU_0%7D%7B%5Csqrt%7B%5Comega%5E2%5Cfrac%7BN_1%5E2N_2%5E2%7D%7BL_0%7D(1-c%5E2)%2B%5Cfrac%7BN_1%5E2%7D%7BN_2%5E2%7DR_2%5E2%7D%7D%5Ccos(%5Comega%20t-arctg%5Cfrac%7B%5Comega%20N_2%5E2(1-c%5E2)L_0%7D%7BR_2%7D)%5Cxrightarrow%5Bc%5Cto%201%5D%7B%7D)
![\xrightarrow[c\to 1]{} -\frac{N_2}{N_1}\frac{U_0\cos \omega t}{R_2}](https://tex.s2cms.ru/svg/%5Cxrightarrow%5Bc%5Cto%201%5D%7B%7D%20-%5Cfrac%7BN_2%7D%7BN_1%7D%5Cfrac%7BU_0%5Ccos%20%5Comega%20t%7D%7BR_2%7D)
В случае с механической моделью этой схемы
![[I_2]=\frac{-b[U_0]}{\sqrt{\frac{\omega^2}{k_{12}^2}+(\frac{k_2}{k_{12}}+1)^2[R_2]^2}}\cos(\omega t-arctg\frac{\omega}{(k_2+k_{12})[R_2]})\xrightarrow[k_{12}\to \infty]{} \frac{-b[U_0]\cos \omega t}{[R_2]}](https://tex.s2cms.ru/svg/%5BI_2%5D%3D%5Cfrac%7B-b%5BU_0%5D%7D%7B%5Csqrt%7B%5Cfrac%7B%5Comega%5E2%7D%7Bk_%7B12%7D%5E2%7D%2B(%5Cfrac%7Bk_2%7D%7Bk_%7B12%7D%7D%2B1)%5E2%5BR_2%5D%5E2%7D%7D%5Ccos(%5Comega%20t-arctg%5Cfrac%7B%5Comega%7D%7B(k_2%2Bk_%7B12%7D)%5BR_2%5D%7D)%5Cxrightarrow%5Bk_%7B12%7D%5Cto%20%5Cinfty%5D%7B%7D%20%5Cfrac%7B-b%5BU_0%5D%5Ccos%20%5Comega%20t%7D%7B%5BR_2%5D%7D)
где величины в квадратных скобках следует заменить их механическими аналогами.
Как и ожидалось, жесткость первой пружинки ни какой роли не играет (при любом c).
Если упростить механический аналог этой схемы, то у нас получится невесомый кораблик на воде, через пружинку привязанный к берегу, и который через другую пружинку и рычаг двигают туда-сюда по гармоническому закону.

Из нелинейных элементов диод можно храповиком замоделировать, операционный усилитель (который работает так: если напряжение на входе + больше чем напряжение на входе -, то он выдает +U, а если наоборот, то -U) — как на картинке, а транзистор — я не придумал как.

В моделях резистора, диода и одиночной катушки можно обойтись без дифференциала. Если пофантазировать, трение валов в креплениях можно интерпретировать как ток утечки через изолятор провода, деформацию валов — как паразитную индуктивность проводов, а момент инерции валов — как паразитную емкость. А вот модели проводов в себе не содержат сопротивления — они сверхпроводящие.
Было бы прикольно, если б кто-нибудь в реальности что-нибудь такое сделал (например из лего-техника, или на 3d принтере напечатал), да на ютуб выложил.
Электрические цепи можно описать следующими уравнениями:
для катушки
для конденсатора
для резистора
(Напряжение падения на катушке равно минус ЭДС)
В механике есть следующие уравнения:
для массивного тела
для пружины
для вязкого трения
(Внешняя сила, действующая на пружину равна минус силе состороны пружины, если в точке приложение силы нет массы)
Как вы наверно догадались, электрические и механические величины можно сопоставить двумя способами:
| электро | мех.1 | мех.2 |
|---|---|---|
| U | F | v |
| I | v | F |
| Ф | p | x |
| Q | x | p |
| L | m | 1/k |
| C | 1/k | m |
| R |
Обычно, когда пытаются провести электро-механическую аналогию, используют первый способ, хотя кое-где можно встретить и второй, им-то мы и воспользуемся.
Но мы будем моделировать во вращательной механике, где каждую поступательную величину мы заменим соответствующим моментом или угловой величиной:
, где
— угловая жесткость
, где
— угловая вязкость
Но для простоты обозначать будем как в поступательной механике:
- напряжение
— скоростью вращения вала
- силу тока
— моментом сил, возникающим в валу
- магнитный поток через катушку
— угловой деформацией пружинки
- заряд конденсатора
— моментом импульса маховика
- индуктивность катушки
— обратной угловой жесткости пружинки
- емкость конденсатора
— моментом инерции маховика
- сопротивление резистора
— обратной углового коэффициента вязкого трения чего-то в чем-то
Так как в электричестве есть понятия потенциал (в точке) и напряжение (между точками), потенциал мы будем моделировать скоростью вращения вала, а напряжение — разностью скоростей двух валов. Ее можно получить при помощи дифференциала (как в автомобиле), у которого один из боковых валов инвертирован:

Выше были изложены пространные теоретические рассуждения, почему мы будем делать именно так. Дальше будет непосредственно описано, как мы это будем делать.
Перейдем к моделированию электрических компонентов:
Источник напряжения
Можно моделировать как вал, вращающийся с постоянной скоростью (который ну ни как невозможно остановить), и подключенный к разностному входу дифференциала. С двух других его концов можно снимать напряжение (они крутятся друг относительно друга с постоянной скоростью).
Источник тока
То же самое, но только используется вал, выдающий постоянный крутящий момент. Такой вал без нагрузки будет разгонятся до бесконечно большой скорости вращения.
Резистор я бы замоделировал так:
От дифференциала идут лопасти и опускаются в стакан с жидкостью.

Чем более вязкая жидкость — тем больше проводимость, тем меньше сопротивление. Между несоединенными валами бесконечное сопротивление. А у резистора, у которого заклинило лопасти — сопротивление нулевое. Можно пофантазировать о напряжении пробоя, и трении между валом и его держателями, но по моему это сходство как-то не очень.
Конденсатор — маховик, присоединенный к дифференциалу

Так же как и в идеальном конденсаторе нет тока утечки, также и в его модели совсем нет трения. Так же как сила тока заряжает конденсатор, так же момент сил между валами разгоняет маховик. В таком конденсаторе на одной пластине всегда заряд
Также емкостью может обладать одиночная сфера (или проводник другой формы). Если он заряжен зарядом Q, то на его поверхности будет потенциал
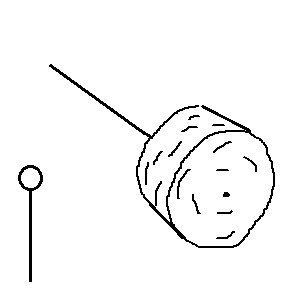
Катушка — пружинкой, присоединенной к дифференциалу
(«Заземлением» будем обозначать неподвижные части конструкции)
Где v — разность скоростей двух валов, а x — их относительное смещение.
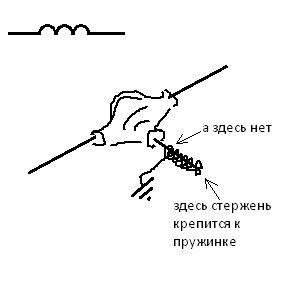
Если считать, что жесткость пружинки достаточно велика, а момент сил, передаваемый из одного вала в другой, достаточно мал, то катушку можно замоделировать так:
Если пофантазировать, то можно провести аналогию между петлей гистерезиса ферромагнетиков и неупругой деформацией пружинки. Правда в ферромагнетиках нет аналога усталости металла.
А также, модель катушки можно использовать как модель амперметра, если присоединить стрелку к выходу дифференциала.
Ее направление отклонения от положения равновесия будет свидетельствовать о том, в какую сторону вал №1 толкает вал №2. А ее величина — о моменте сил, с которым один вал воздействует на другой, т.е. о силе тока через моделируемую катушку.
И из казалось бы самого простого закона
В принципе в катушке можно обойтись без дифференциала, но в трансформаторе, который содержит в себе пару катушек, так уже не получится.

Рассмотрим парочку переходных процессов.
Источник напряжения, ключ, резистор, (изначально незаряженный) конденсатор.

Изначально конденсатор не заряжен.
Включаем ключ (после этого
Изначально маховик покоится.
Включаем ключ (после этого сумма скоростей маховика и лопастей резистора равна скорости источника напряжения), маховик в начальный момент покоится, а лопасти резистора (невесомые) начинают вращаться, но из-за трения возникает момент сил, который разгоняет маховик. Чем быстрее крутится маховик, тем медленнее крутятся лопасти резистора, и тем с меньшей силой вращают маховик. Если через некоторое время ключ разомкнуть, то маховик продолжит вращаться не меняя своей скорости, а скорость лопастей резистора упадет до 0.
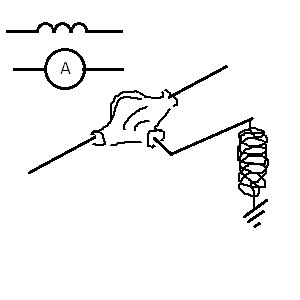
Источник напряжения, ключ, резистор, катушка.
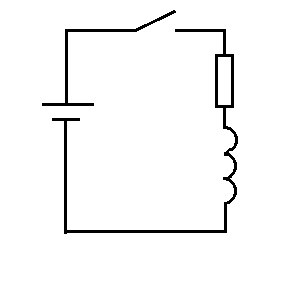
Вначале ток равен нулю. Мы включаем ключ (после этого
Вначале пружинка не растянута. Мы включаем ключ (после этого сумма скоростей деформации пружинки и лопастей резистора равна скорости источника напряжения), и пружинка начинает растягиваться так, как будто в самый начальный момент сопротивление резистора =0. Уже растянутая пружинка начинает оказывать силу на резистор, в результате чего в резисторе возникает разность скоростей, а в пружинке разность скоростей начинает уменьшаться. Чем больше пружинка натянута, тем большую силу она оказывает на резистор, тем больше разность скоростей в резисторе, и тем меньше разность скоростей в катушке (вернее в ее модели), и тем медленнее растягивается пружинка катушки дальше. Если через некоторое время ключ разомкнуть, то в результате практически мгновенного падения нагрузки на пружинку, она очень быстро сожмется в исходное положение.
Механическую модель можно упростить, представив себе покоящуюся на воде невесомую лодку, к которой прикреплена пружинка, а другой конец пружинки внезапно начинают тянуть с постоянной скоростью. Вначале лодка покоится. Потом пружинка начинает натягиваться, и чем больше натягивается, тем больше увлекает за собой лодку, и тем меньше разность между скоростями двух концов пружинки. А если пружинку отпустить (масса кораблика и масса пружинки =0), то кораблик тут же остановится, а пружинка тут же сожмется.

И, наконец, механическая модель трансформатора.
Сам трансформатор описывается также как катушка:
где
- U — столбец напряжений
и
на 1й и 2й катушках.
- Ф — столбец магнитных потоков
и
через 1ю и 2ю катушку.
- I — столбец токов
и
через 1ю и 2ю катушку.
- L — симметричная (
) матрица взаимных индуктивностей
между соответствующими катушками.
Иначе говоря трансформатор описывается системой уравнений:
И чтобы получить механическую модель трансформатора, достаточно взять механические модели двух катушек, и соединить их пружинкой через рычаг:
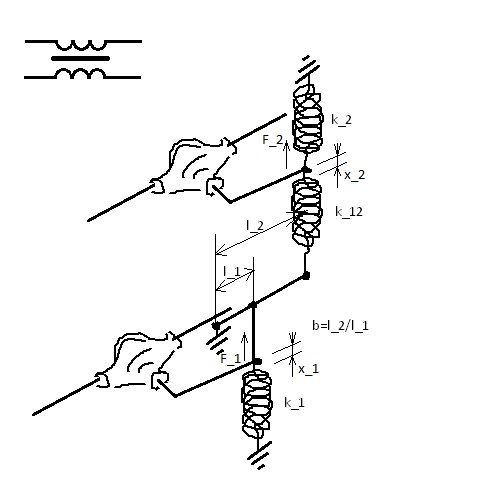
Можно все поступательные пружинки заменить на вращательные, а рычаг заменить на редуктор:

Найдем уравнения, описывающие эту систему.
Предположим, что нижнее плечо сместилось вверх на
что тоже самое с
ее можно разрешить относительно
где
Сравнивая эту систему с (1) получается, что матрицу
следует сопоставлять с матрицей
И если у нас есть трансформатор, у которого все витки одинаковые по форме и сечению, на 1й обмотке
где
Если в его модели взять
отношения жесткостей пружин будут выглядеть так:
а матрица индуктивностей модели так:
т.к.
то соотношения жесткостей тоже >0 (если исключить из модели рычаг, т.е. b=1, то одно из этих соотношений окажется отрицательным, а пружин с отрицательной жесткостью не бывает).
И обратно: при любых соотношения жесткостей пружин
и при любом соотношении плеч рычага b>0
При
При
Для примера работы трансформатора рассмотрим схему: источник переменного напряжения, трансформатор, резистор
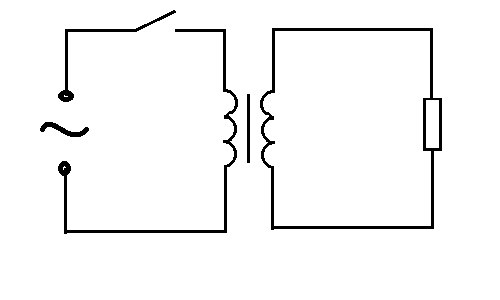
и рассчитаем ее
->
пусть
тогда
последнее уравнение можно переписать в виде
OPOC:
Этот вклад будет виден только сразу после включения схемы, потом затухнет и не будет участвовать в установившемся режиме трансформации.
Если изменить уравнение так:
и искать ЧРНС в виде
=>
т.к.
В случае с механической моделью этой схемы
где величины в квадратных скобках следует заменить их механическими аналогами.
Как и ожидалось, жесткость первой пружинки ни какой роли не играет (при любом c).
Если упростить механический аналог этой схемы, то у нас получится невесомый кораблик на воде, через пружинку привязанный к берегу, и который через другую пружинку и рычаг двигают туда-сюда по гармоническому закону.

Нелинейные элементы
Из нелинейных элементов диод можно храповиком замоделировать, операционный усилитель (который работает так: если напряжение на входе + больше чем напряжение на входе -, то он выдает +U, а если наоборот, то -U) — как на картинке, а транзистор — я не придумал как.

Вместо заключения
В моделях резистора, диода и одиночной катушки можно обойтись без дифференциала. Если пофантазировать, трение валов в креплениях можно интерпретировать как ток утечки через изолятор провода, деформацию валов — как паразитную индуктивность проводов, а момент инерции валов — как паразитную емкость. А вот модели проводов в себе не содержат сопротивления — они сверхпроводящие.
Было бы прикольно, если б кто-нибудь в реальности что-нибудь такое сделал (например из лего-техника, или на 3d принтере напечатал), да на ютуб выложил.