На сайте бесплатных лекций MIT OpenCourseWare выложен курс лекций по космологии Алана Гуса, одного из создателей инфляционной модели вселенной.
Вашему вниманию предлагается перевод пятой лекции: «Космологическое красное смещение и динамика однородной расширяющейся вселенной, часть 1».
Сегодня мы закончим рассмотрение кинематики однородно расширяющейся вселенной, которую мы обсуждали в прошлый раз. Единственный вопрос из этой темы, который мы еще не затрагивали — это космологическое красное смещение. Затем мы перейдем к динамике однородного расширения — каким образом гравитация влияет на расширение вселенной. Это будет основной темой сегодняшней и нескольких следующих лекций.
Напомню, что в конце последней лекции речь шла о синхронизации часов в системе координат, которую мы будем использовать для описания однородно расширяющейся вселенной. Вспомним, что мы ввели сопутствующие координаты, которые расширяются вместе со вселенной. Мы будем предполагать, что вселенная совершенно однородна и изотропна, и все объекты покоятся в этой системе координат.
В реальной вселенной имеется некоторое движение вещества относительно этой системы координат, потому что вселенная не совсем однородна. Но сейчас мы будем работать с приближением, в котором наша модельная вселенная абсолютно однородна и все вещество покоится относительно расширяющейся системы координат.
Теперь вспомним, как мы определили космологическое время на прошлой лекции. Представим себе, что в каждой точке вселенной имеются часы, находящиеся в покое относительно вещества, а значит и расширяющейся сопутствующей системы координат. Все такие часы измеряют локальное время, и мы хотим договориться о их синхронизации. В прошлый раз мы выяснили, что можем синхронизировать часы, если имеются какие-нибудь космологические явления, которые можно увидеть из любой точки вселенной, и которые меняются со временем. Мы привели два примера: один — изменение постоянной Хаббла, которую можно измерить локально и договориться установить свои часы на ноль, когда постоянная Хаббла примет определенное значение.
Второй пример — температура космического микроволнового фонового излучения. В нашей модельной вселенной можно договориться установить свои часы на ноль, когда температура космического фонового излучения достигнет 5 градусов или любого заданного числа. Если имеются подобные явления, а они есть в нашей вселенной, то можно синхронизировать все часы. Важно понимать, что как только часы будут однажды синхронизированы, они останутся синхронизированными вследствие нашего предположения об однородности. То есть, если все договорятся, что температура космического фонового излучения в нулевое время равна 10 градусам, и все подождут 15 минут, то все увидят одно и то же падение температуры в течение этого промежутка времени, иначе это было бы нарушением нашей гипотезы об абсолютной однородности.
СТУДЕНТ: Верно ли, что температура фонового излучения одинакова для всех инерциальных наблюдателей?
ПРЕПОДАВАТЕЛЬ: Она не совсем одинакова для разных инерциальных наблюдателей. Она одинакова для привилегированного класса наблюдателей, которые находятся в покое относительно усредненного распределения вещества и, значит, относительно сопутствующей системы координат. Если вы начнете перемещаться через космическое фоновое излучение, то вы больше не будете видеть равномерное распределение температуры. Вы увидите излучение более горячее в одном направлении и более холодное в обратном. На самом деле, как я уже упоминал, мы видим этот эффект в нашей реальной вселенной. Мы, по-видимому, движемся относительно космического фонового излучения, примерно с 1/1000 от скорости света. Так что температура излучения не инвариантна по отношению к движению наблюдателя.
Можно задаться другим вопросом – одинакова ли температура фонового излучения в различных местах видимой вселенной? Насколько мы можем судить, да. Существует прямой способ измерения температуры фонового излучения, о котором мы, возможно, поговорим позже в курсе, при помощи наблюдения за определенными спектральными линиями в далеких галактиках. В некоторых галактиках, где видны эти линии, можно напрямую измерять температуру космического микроволнового фонового излучения. В нашей модели мы предполагаем полную однородность, что все везде одинаково. Хотя однородность в реальной вселенной не полная, есть веские доказательства приближенной однородности нашей вселенной.
СТУДЕНТ: Если некоторые наблюдатели живут рядом с черными дырами, повлияет ли это на синхронизацию часов для таких наблюдателей?
ПРЕПОДАВАТЕЛЬ: конечно, повлияет. Можно космологически синхронизировать часы, только предполагая, что вселенная абсолютно однородна. Как только появляются неоднородности, такие как черные дыры, или даже просто звезды, подобные Солнцу, они создают отклонения, которые препятствуют синхронизации часов друг с другом. Как только появляется концентрация массы, однородность становится лишь приблизительной. Но эти отклонения невелики. Отклонения, возникающие из-за Солнца, составляют порядка одной миллионной. Поэтому, в очень хорошем приближении вселенная описывается нашей однородной моделью. Хотя, если очень приблизиться к одной из сверхмассивных черных дыр, находящихся в центрах галактик, окажется, что она оказывает очень сильное влияние на ход ваших часов.
Следующая тема, как я и обещал — космологическое красное смещение. В третьей лекции, мы говорили о доплеровском сдвиге для звуковых волн и о релятивистском доплеровском сдвиге для световых волн, с учетом специальной теории относительности. Однако, космология не полностью описывается специальной теорией относительности, хотя специальная теория относительности используется для описания локальных событий в космологии. Специальная теория относительности не включает в себя эффекты гравитации, а в глобальном масштабе эффекты гравитации очень важны для космологии. Поэтому специальной теории относительности недостаточно, чтобы понять многие свойства вселенной, включая космологическое красное смещение. Однако оказывается, что есть способ описания космологического красного смещения, который объясняет его еще проще, чем специальная теория относительности. Сначала я опишу его, а затем мы поговорим о том, как этот очень простой на вид результат соотносится с выводом специальной теории относительности, который также должен быть правильным, по крайней мере, локально.
Итак, предположим, что мы смотрим на далекую галактику, и свет излучается источником, находящимся в этой галактике. Мы хотим понять, какова зависимость между частотой света при излучении, и частотой, которую мы увидим при получения света.

Чтобы представить себе эту ситуацию, давайте введем систему координат, . Это будет наша сопутствующая система координат.
. Это будет наша сопутствующая система координат.  измеряется в делениях. Мы поместим себя в начало координат, а удаленную галактику на некотором удалении от нас. Она имеет определенную координату
измеряется в делениях. Мы поместим себя в начало координат, а удаленную галактику на некотором удалении от нас. Она имеет определенную координату  (
( обозначает сопутствующий).
обозначает сопутствующий).  – это сопутствующее расстояние от нас до галактики. Физическое расстояние, которое мы назовем
– это сопутствующее расстояние от нас до галактики. Физическое расстояние, которое мы назовем  (
( означает физический), зависит от времени, потому что вселенная расширяется. Как мы уже говорили,
означает физический), зависит от времени, потому что вселенная расширяется. Как мы уже говорили,  . Масштабный фактор
. Масштабный фактор  , который зависит от времени, умножается на сопутствующее расстояние, которое не зависит от времени. Таким образом, физические расстояния просто увеличиваются пропорционально масштабному фактору
, который зависит от времени, умножается на сопутствующее расстояние, которое не зависит от времени. Таким образом, физические расстояния просто увеличиваются пропорционально масштабному фактору  .
.
Предположим теперь, что галактика излучает световую волну, и мы пытаемся определить расстояние между гребнями волны, которое равно длине волны. Поскольку нас будут интересовать только гребни, мы просто представим, что каждый гребень — это импульс, и то, что происходит между ними, нас не интересует. Мы будем следить за последовательными световыми импульсами, излучаемыми галактикой.
Важно, что мы знаем для нашей модели, как распространяются световые волны в сопутствующей системе координат. Если — сопутствующая координата, то
— сопутствующая координата, то  – сопутствующая скорость света, которая равна обычной скорости света
– сопутствующая скорость света, которая равна обычной скорости света  , но деленной на масштабный фактор:
, но деленной на масштабный фактор:
Масштабный фактор здесь играет роль преобразования метров в деления. измеряется в метрах в секунду. Деля
измеряется в метрах в секунду. Деля  на
на  мы получаем скорость света в делениях в секунду, как и хотели, потому что
мы получаем скорость света в делениях в секунду, как и хотели, потому что  измеряется не в метрах, а в делениях. Деление — это произвольная единица, которую мы выбираем для описания нашей сопутствующей системы координат.
измеряется не в метрах, а в делениях. Деление — это произвольная единица, которую мы выбираем для описания нашей сопутствующей системы координат.
Важная особенность этого уравнения, заключается в том, что скорость света в сопутствующей системе координат зависит от времени, но не зависит от . Наша вселенная однородна, поэтому все точки
. Наша вселенная однородна, поэтому все точки  равнозначны. Поэтому, в каждый момент времени два световых импульса будут двигаться с одинаковой сопутствующей скоростью, независимо от того, где они находятся. Это все, что нам нужно. Первый импульс покидает удаленную галактику и движется к нам, второй импульс следует за первым. Второй импульс в любой момент времени будет двигаться с той же сопутствующей скоростью, что и первый импульс, даже если его сопутствующая скорость меняется со временем.
равнозначны. Поэтому, в каждый момент времени два световых импульса будут двигаться с одинаковой сопутствующей скоростью, независимо от того, где они находятся. Это все, что нам нужно. Первый импульс покидает удаленную галактику и движется к нам, второй импульс следует за первым. Второй импульс в любой момент времени будет двигаться с той же сопутствующей скоростью, что и первый импульс, даже если его сопутствующая скорость меняется со временем.
Это означает следующее. Сопутствующая скорость импульсов может меняться со временем, но до тех пор, пока они оба двигаются с одинаковой сопутствующей скоростью, в любой момент времени они будут находиться ровно на одном и том же расстоянии друг от друга в сопутствующей системе координат. , сопутствующее расстояние между двумя импульсами, не меняется со временем. Если сопутствующее расстояние не меняется со временем, а физическое расстояние всегда равно произведению масштабного фактора на сопутствующее расстояние, то физическая длина волны светового импульса будет просто растянута пропорционально масштабному фактору. Длина волны будет увеличиваться вместе с расширением вселенной, точно так же, как любое другое расстояние в нашей модели вселенной будет увеличиваться по мере расширения вселенной. Это ключевая идея, она очень проста, и в ней все содержится.
, сопутствующее расстояние между двумя импульсами, не меняется со временем. Если сопутствующее расстояние не меняется со временем, а физическое расстояние всегда равно произведению масштабного фактора на сопутствующее расстояние, то физическая длина волны светового импульса будет просто растянута пропорционально масштабному фактору. Длина волны будет увеличиваться вместе с расширением вселенной, точно так же, как любое другое расстояние в нашей модели вселенной будет увеличиваться по мере расширения вселенной. Это ключевая идея, она очень проста, и в ней все содержится.
То, что постоянно, означает, что
постоянно, означает, что  , физическое расстояние, пропорционально
, физическое расстояние, пропорционально  , а это означает, что длина волны света
, а это означает, что длина волны света  , как функция от t, пропорциональна
, как функция от t, пропорциональна  .
.
Длина волны связана с периодом волны отношением . Длина волны — это расстояние, которое волна проходит за один период. Поэтому, если
. Длина волны — это расстояние, которое волна проходит за один период. Поэтому, если  пропорциональна
пропорциональна  , то и
, то и  , период волны, будет пропорционален
, период волны, будет пропорционален  . Поэтому:
. Поэтому:
Таким образом, отношение длин волн — это просто число раз, в которое вселенная растянулась. Оно равно отношению масштабных факторов в начальное и конечное время. Мы определяли красное смещение при помощи периода волны. Отношение периодов, или отношение длин волн, или отношение масштабных факторов, равняется 1 + z.
Связь космологического красного смещения со специальной теорией относительности
Каким образом космологическое красное смещение связано с красным смещением специальной теории относительности, формулу для которого мы вывели ранее? Наш результат отличается в двух отношениях от расчета, который мы сделали на третей лекции. Первая причина, которая важна для нас, это то, что космологический расчет учитывает эффекты, которые не были приняты во внимание предыдущими расчетами. В частности, несмотря на то, что мы получили ответ при помощи очень простого кинематического аргумента, в котором, на первый взгляд, практически нет никакой математики, он на самом деле очень сильный, поскольку он учитывает не только специальную теорию относительности, но и общую теорию относительности. Он включает в себя все эффекты гравитации. Гравитация не влияет на факт, что сопутствующая скорость света равна . Это всего лишь преобразование единиц, вместе с фундаментальным физическим предположением, что скорость света всегда равна
. Это всего лишь преобразование единиц, вместе с фундаментальным физическим предположением, что скорость света всегда равна  относительно любого наблюдателя.
относительно любого наблюдателя.
Поэтому, когда мы учитываем гравитацию, это соотношение продолжает сохраняться, а это было единственное, что мы использовали, так что гравитация не может повлиять на ответ. Не упустили ли мы что-нибудь из специальной теории относительности? Я не учел замедление времени, которое имело решающее значение для нашего релятивистского вычисления красного смещения.
Сделал ли я ошибку? Нужно ли куда-нибудь добавить замедление времени? На самом деле, нет. У нас было двое часов, задействованных в нашем расчете: часы в галактике и наши часы, которые мы использовали для измерения периода излучения и периода приема. Но оба этих часов находятся в покое относительно локального вещества, даже несмотря на то, что они движутся относительно друг друга. Поэтому, по определению, они измеряют космологическое время. Космологическое время — это очень своеобразный вид времени, это не время в какой-либо инерциальной системе. Часы двигаются относительно друг друга, поэтому, если бы мы определяли время в инерционной системе, такие часы никогда не могли бы быть синхронизированы и время бы на них не совпадало.
Но в системе космологического времени, они показывают одно и то же время. Поскольку каждые часы находятся в покое относительно локального вещества, они измеряют , космологическое время. Таким образом, не нужно никакого замедления времени. Дело не в том, что мы его забыли, его там нет. Оно не используется при вычислениях.
, космологическое время. Таким образом, не нужно никакого замедления времени. Дело не в том, что мы его забыли, его там нет. Оно не используется при вычислениях.
Таким образом, полученный результат, каким бы простым он ни казался, на самом деле полностью охватывает эффекты как специальной теории относительности, так и гравитации. Позвольте заметить, что не очевидно, где здесь гравитация. Я сказал вам, что результат включает в себя все эффекты гравитации. Где же спрятана гравитация? Я хочу задать этот вопрос вам. Каким образом гравитация влияет на вычисления, несмотря на то, что я не упоминал гравитацию, когда делал расчет?
СТУДЕНТ: Через масштабный фактор.
ПРЕПОДАВАТЕЛЬ: Правильно, через масштабный фактор. Мы еще не говорили о том, как меняется . Изменение
. Изменение  будет явно включать в себя эффекты гравитации. Вот почему наш результат зависит от гравитации, хотя нам не нужно было использовать или упоминать гравитацию, чтобы получить ответ. Ответ для космологического красного смещения получился настолько простым, потому что
будет явно включать в себя эффекты гравитации. Вот почему наш результат зависит от гравитации, хотя нам не нужно было использовать или упоминать гравитацию, чтобы получить ответ. Ответ для космологического красного смещения получился настолько простым, потому что  уже включает в себя много информации. Мы просто воспользовались этим, чтобы получить очень простое выражение, зависящее от
уже включает в себя много информации. Мы просто воспользовались этим, чтобы получить очень простое выражение, зависящее от  , не говоря пока ничего о том, как мы будем вычислять
, не говоря пока ничего о том, как мы будем вычислять  . Это первое отличие.
. Это первое отличие.
Другое важное различие между этими двумя вычислениями — это используемые в ответе переменные. На один и тот же вопрос может быть несколько разных ответов, в зависимости от того, какие используются переменные. В данном случае мы выражаем красное смещение для объектов, покоящихся в сопутствующей системе координат. Расчет в специальной теории относительности, с другой стороны, дает z в зависимости от скорости, измеренной в инерциальной системе координат. Таким образом, результаты выражаются в совершенно разных терминах.
для объектов, покоящихся в сопутствующей системе координат. Расчет в специальной теории относительности, с другой стороны, дает z в зависимости от скорости, измеренной в инерциальной системе координат. Таким образом, результаты выражаются в совершенно разных терминах.
Что будет, если мы попытаемся сравнить ответы, которые мы получили для релятивистского и для космологического красного смещения? Имеется только один случай, в котором их правомерно сравнивать. Поскольку расчет, который мы только что сделали, включает эффекты гравитации, а расчет при помощи специальной теории относительности не включает эффектов гравитации, единственным случаем, при котором мы можем их сравнить и убедиться, что они совпадают, является случай, когда гравитация пренебрежимо мала.
Можно рассматривать космологическую модель, где гравитация мала, в этом нет никакого противоречия. Если гравитация незначительна, как будет вести себя ? Если нет гравитации,
? Если нет гравитации,  должна линейно зависеть от
должна линейно зависеть от  . Это означает, что все скорости постоянны. Таким образом, в частном случае отсутствия гравитации,
. Это означает, что все скорости постоянны. Таким образом, в частном случае отсутствия гравитации,  растет линейно со временем. При этом всегда можно сделать так, чтобы константа, которая добавляется к линейному члену, стала нулем, просто установив нулевое время в момент, когда
растет линейно со временем. При этом всегда можно сделать так, чтобы константа, которая добавляется к линейному члену, стала нулем, просто установив нулевое время в момент, когда  равна нулю. Таким образом, при отсутствии гравитации можно сказать, что
равна нулю. Таким образом, при отсутствии гравитации можно сказать, что  должна быть пропорциональна t.
должна быть пропорциональна t.
Тогда для этого частного случая, наши два расчета должны совпасть. Вы можете это сами проверить. Это не так просто, для этого понадобится понимание взаимосвязи между двумя системами координат. Ответ специальной теории относительности дается в инерциальной системе координат, которая при наличии гравитации вообще не существует. Она связана с расширяющейся системой координат сложным образом, из-за замедления времени и Лоренцева сокращения, связанных с движением, которое происходит в расширяющейся вселенной.
Вам нужно будет выяснить взаимосвязь между этими двумя системами координат. Когда вы это сделаете, и сравните ответы, то обнаружите, что они действительно точно совпадают. Все это прекрасно согласуется со специальной теорией относительности, в частном случае, когда гравитация отсутствует.
Мы обсудили все, что я хотел рассказать о кинематике однородно расширяющейся вселенной, теперь мы готовы перейти к динамике. Нам нужно выяснить, каким образом гравитация влияет на вселенную, чтобы иметь возможность вычислить, как меняется со временем. Это будет единственная цель, понять поведение
меняется со временем. Это будет единственная цель, понять поведение  .
.
Этот вопрос, в некотором смысле, восходит к Исааку Ньютону. Хочу заметить, что одна из интересных вещей в космологии заключается в том, что, если посмотреть на историю космологии, многие великие физики допускали большие ошибки, пытаясь проанализировать космологические вопросы. Сегодня мы обсудим одну из ошибок Ньютона. Даже такие великие физики, как Ньютон, могли совершать глупые ошибки. Он действительно совершил глупую ошибку, анализируя космологические последствия своей собственной теории гравитации.
Ньютон, как и все до Хаббла считал, что вселенная статична. Он представлял вселенную как статичное распределение звезд, разбросанных в пространстве. В начале своей карьеры, насколько я знаю историю, он предполагал, что распределение звезд было конечным в бесконечном пространстве. Но в какой-то момент он понял, что если имеется конечное распределение массы в пустом пространстве, а все вещество притягивается друг к другу с силой притяжения обратно пропорциональной квадрату расстояния, о которой он знал, поскольку он открыл ее, в результате все должно сжаться в точку. Он решил, что его предположение не работает, но все равно он был уверен, что вселенная статична, поскольку все выглядело статично, звезды никуда не двигались.
Поэтому он задался вопросом, что можно изменить, и решил, что вместо того, чтобы предполагать, что звезды образуют конечное распределение, лучше предположить, что они распределены бесконечно в пространстве. Он рассуждал следующим образом, а это как раз и является заблуждением, что если звезды заполняют бесконечное пространство, то, даже если все они будут притягивать друг друга, у них не будет предпочтительного направления для движения. Поскольку у них не будет предпочтительного направления для движения, потому что на них действует притяжение со всех сторон, они остаются на месте. Таким образом, он полагал, что бесконечное, равномерное распределение вещества будет стабильным, что не будет никаких гравитационных сил, возникающих в таком бесконечном распределении массы.
Он, по-видимому, слышал разные аргументы в пользу этого. Один из аргументов, что бесконечное распределение будет стабильным, был аргумент, что на частицу действует бесконечная сила тянущая ее вправо и бесконечная сила, тянущая ее влево. Так как обе они бесконечны, они нейтрализуют друг друга. Ньютон не принял этот аргумент. Он был достаточно искушенным, чтобы понять, что бесконечность минус бесконечность не обязательно равна нулю. Тем не менее, Ньютон был убежден, что бесконечное распределение массы будет стабильным.
Аргумент, который убедил его, был не бесконечностью вещества с каждой стороны, а симметрией. Аргумент, который он принимал, заключался в том, что, если посмотреть на любую точку этого бесконечного распределения, если посмотреть вокруг этой точки, все направления будут выглядеть одинаково, с веществом, простирающейся до бесконечности, и поэтому не будет направления, в котором сила должна действовать на любую конкретную частицу. А если у силы нет направления, она должна быть равна нулю. Это был аргумент, который принимал Ньютон.
Сейчас мы обсудим это более подробно и попытаемся понять, как современные ученые относятся к этому аргументу. Кстати, хочу упомянуть исторический факт. Аргумент Ньютона, насколько мне известно, не подвергался сомнению ни у кого в течение сотен лет, вплоть до Альберта Эйнштейна. Альберт Эйнштейн, пытаясь описать космологию при помощи своей новой общей теории относительности, был первым человеком, осознавшим, что даже если у вас бесконечное распределение массы, она сколлапсирует. Эйнштейн понял, что то же самое произойдет и в Ньютоновской физике, это не особенность общей теории относительности. Просто исторически потребовалось создание общей теории относительности, чтобы заставить людей переосмыслить и понять, что Ньютон был неправ.
Трудность попытки проанализировать проблему так, как это сделал Ньютон, заключается в том, что Ньютон рассматривал гравитацию как силу, действующую на расстоянии. Если у нас есть два объекта, расположенных на расстоянии друг от друга, они будут притягивать друг друга с силой пропорциональной
друг от друга, они будут притягивать друг друга с силой пропорциональной  . Со времен Ньютона были придуманы другие способы описания Ньютоновской гравитации, которые делают происходящее гораздо более ясным. Трудность в использовании описания Ньютона заключается в том, что, если мы пытаемся сложить все эти силы, пропорциональные
. Со времен Ньютона были придуманы другие способы описания Ньютоновской гравитации, которые делают происходящее гораздо более ясным. Трудность в использовании описания Ньютона заключается в том, что, если мы пытаемся сложить все эти силы, пропорциональные  , мы получим расходящиеся суммы, интерпретацию которых нам нужно понять. Но чтобы понять, что Ньютон был не прав, проще всего взглянуть на другие формулировки гравитации Ньютона. Я опишу две из них, с обоими из которых, вы, возможно, уже знакомы.
, мы получим расходящиеся суммы, интерпретацию которых нам нужно понять. Но чтобы понять, что Ньютон был не прав, проще всего взглянуть на другие формулировки гравитации Ньютона. Я опишу две из них, с обоими из которых, вы, возможно, уже знакомы.
Первую я опишу по аналогии с законом Кулона. Закон Кулона действительно такой же, как закон силы тяжести. Закон Кулона гласит, что любая заряженная частица создает электрическое поле, которое равно заряду, деленному на расстояние в квадрате и умноженному на единичный вектор, направленный от заряда.
Это закон Кулона. Иногда в нем стоит константа, в зависимости от того, в каких единицах измеряется , но это для нас не важно. Я предполагаю, что мы используем это уравнение, где константа равна 1.
, но это для нас не важно. Я предполагаю, что мы используем это уравнение, где константа равна 1.
Как известно, из закона Кулона можно получить закон Гаусса. Если закон Кулона верен, то можно однозначно сказать, чему равен интеграл потока электрического поля по любой замкнутой поверхности. Он пропорционален общей сумме заряда внутри поверхности.
где равен общей сумме заряда внутри замкнутой поверхности.
равен общей сумме заряда внутри замкнутой поверхности.
Можно записать закон тяготения Ньютона, почти так, как его сформулировал Ньютон. Можно выразить гравитационное ускорение на заданном расстоянии от объекта:
Это такой же закон обратных квадратов и похож на закон Кулона, за исключением константы в начале. Константа имеет противоположный знак, что важно в некоторых случаях, но не сейчас. Важным является то, что это уравнение может быть переформулировано как закон Гаусса, и оно называется законом гравитации Гаусса. Единственное, чем оно отличается – это константа впереди:
Теперь давайте возьмем однородное распределение вещества, которое рассматривал Ньютон. Ньютон утверждал, что можно взять однородное распределение вещества, заполняющее все бесконечное пространство, и оно будет статично, то есть не будет ускорения. Отсутствие ускорения на языке Ньютона означает, что должно быть везде нулем. Но из последней формулы следует, что если
должно быть везде нулем. Но из последней формулы следует, что если  везде равно нулю, то интеграл от
везде равно нулю, то интеграл от  по любой замкнутой поверхности также будет равен нулю, и, поэтому, общая масса, заключенная внутри этой поверхности, тоже должна быть равна нулю. Но если у нас есть равномерное распределение массы, то суммарная заключенная масса, конечно, не будет равна нулю ни для какого ненулевого объема. Таким образом, ясно, что утверждение, что система статична, прямо противоречит формулировке Гаусса закона тяготения Ньютона.
по любой замкнутой поверхности также будет равен нулю, и, поэтому, общая масса, заключенная внутри этой поверхности, тоже должна быть равна нулю. Но если у нас есть равномерное распределение массы, то суммарная заключенная масса, конечно, не будет равна нулю ни для какого ненулевого объема. Таким образом, ясно, что утверждение, что система статична, прямо противоречит формулировке Гаусса закона тяготения Ньютона.
Просто ради интереса, я приведу вам еще один похожий аргумент, используя другую более современную формулировку Ньютоновской гравитации. Если вы ее не встречали и не понимаете, о чем я говорю, не беспокойтесь, это не так важно. Для тех из вас, кто с ней знаком, я ее приведу. Другой способ формулировки Ньютоновской гравитации — ввести гравитационный потенциал. Я буду использовать букву для гравитационного потенциала. Он связан с гравитационным ускорением следующим образом:
для гравитационного потенциала. Он связан с гравитационным ускорением следующим образом:  , где
, где  — это градиент
— это градиент  . Градиент
. Градиент  равен единичному вектору
равен единичному вектору  в направлении x умноженному на производную от
в направлении x умноженному на производную от  по
по  , плюс единичному вектору
, плюс единичному вектору  в направлении оси y, умноженному на производную от
в направлении оси y, умноженному на производную от  по
по  , плюс единичному вектору
, плюс единичному вектору  умноженному на производную от
умноженному на производную от  по
по  :
:
Как только мы определили гравитационный потенциал, можно написать дифференциальную форму закона Гаусса, которая становится так называемым уравнением Пуассона. Оно утверждает, что определяется как вторая производная от
определяется как вторая производная от  по
по  , плюс вторая производная от
, плюс вторая производная от  по
по  , плюс вторая производная от
, плюс вторая производная от  по
по  :
:
Это называется уравнением Пуассона. Если задана плотность массы, то можно найти гравитационный потенциал, затем можно вычислить его градиент, и найти . Это эквивалентно другим формулировкам гравитации. Но это дает нам еще одну проверку утверждения Ньютона о том, что существует однородное распределение вещества без каких-либо гравитационных сил. Если нет гравитационных сил, то
. Это эквивалентно другим формулировкам гравитации. Но это дает нам еще одну проверку утверждения Ньютона о том, что существует однородное распределение вещества без каких-либо гравитационных сил. Если нет гравитационных сил, то  должно быть равна нулю, как мы говорили минуту назад. А из того, что
должно быть равна нулю, как мы говорили минуту назад. А из того, что  равно нулю, следует, что градиент
равно нулю, следует, что градиент  равен нулю.
равен нулю.
Если посмотреть на формулу градиента, то это вектор. Для нулевого вектора каждый из трех его компонентов должен быть равен нулю, и, следовательно, производная от по
по  исчезнет, производная от
исчезнет, производная от  по
по  исчезнет и производная от
исчезнет и производная от  по
по  исчезнет. Это значит, что
исчезнет. Это значит, что  должен быть всюду постоянным, он не имеет производной по любой пространственной координате. Поэтому, если
должен быть всюду постоянным, он не имеет производной по любой пространственной координате. Поэтому, если  равно нулю, то градиент
равно нулю, то градиент  равен нулю, и
равен нулю, и  является константой во всем пространстве. Если
является константой во всем пространстве. Если  везде постоянен, что имеет место в случае отсутствия силы тяжести, тогда сразу видно, что
везде постоянен, что имеет место в случае отсутствия силы тяжести, тогда сразу видно, что  должен быть равна нулю, а значит ρ должна быть равна нулю, то есть не будет плотности массы. Но Ньютон хотел иметь ненулевую плотность массы, вещество, равномерно распределенное по бесконечному пространству. Это еще одна демонстрация того, что аргумент Ньютона был неверным.
должен быть равна нулю, а значит ρ должна быть равна нулю, то есть не будет плотности массы. Но Ньютон хотел иметь ненулевую плотность массы, вещество, равномерно распределенное по бесконечному пространству. Это еще одна демонстрация того, что аргумент Ньютона был неверным.
Итак, мы пришли к выводу, что Ньютон был неправ, но нам нужно более тщательно проанализировать аргумент Ньютона, чтобы понять, где именно он ошибся. Следующее, что я хочу обсудить, это неоднозначность, связанная со сложением Ньютоновских гравитационных сил для бесконечной вселенной. Я упомянул, что реальная проблема с вычислениями Ньютона заключается в том, что сумма, которую он вычислял, расходится, и нужно быть осторожным, при попытке ее вычисления.
Чтобы прояснить это, я хочу начать с примера интеграла, который дает неоднозначное значение. Я введу пару математических понятий. Давайте представим, что у нас есть некоторая произвольная функция , где
, где  будет просто одной переменной.
будет просто одной переменной.
Мы обобщим ее на три измерения, что нас и интересует, но начнем с одной переменной. Если у нас есть функция , мы можем рассмотреть интеграл от минус бесконечности до бесконечности от
, мы можем рассмотреть интеграл от минус бесконечности до бесконечности от  , я назову его
, я назову его  :
:
Именно такой интеграл получается при сложении всех гравитационных сил, действующих на тело. Теперь я хочу рассмотреть случай, когда конечен.
конечен.
Мне нужно сначала более точно определить, что я имею в виду под , интегралом от минус до плюс бесконечности. Мы можем определить интеграл от минус бесконечности до бесконечности как предел интеграла от
, интегралом от минус до плюс бесконечности. Мы можем определить интеграл от минус бесконечности до бесконечности как предел интеграла от  до
до  от
от  , при котором
, при котором  стремится к бесконечности:
стремится к бесконечности:
Нам нужно вычислить интеграл от до
до  . Если мы предположим, что
. Если мы предположим, что  конечна, интеграл тоже всегда конечен. Я предположу, что сама функция
конечна, интеграл тоже всегда конечен. Я предположу, что сама функция  конечна, мы будем беспокоиться только о сходимости интеграла при
конечна, мы будем беспокоиться только о сходимости интеграла при  , стремящемся к бесконечности. Итак, для любого заданного
, стремящемся к бесконечности. Итак, для любого заданного  интеграл — это какое-то число. Тогда можно задаться вопросом – стремится ли это число к пределу, когда
интеграл — это какое-то число. Тогда можно задаться вопросом – стремится ли это число к пределу, когда  стремится к бесконечности? Если это так, то мы назовем это значением
стремится к бесконечности? Если это так, то мы назовем это значением  . Это просто определение, что мы подразумеваем под интегралом от минус бесконечности до бесконечности.
. Это просто определение, что мы подразумеваем под интегралом от минус бесконечности до бесконечности.
Теперь рассмотрим случай, когда это значение существует, когда меньше бесконечности, то есть он имеет некоторое конечное значение. Но я хочу также рассмотреть интеграл, который я назову
меньше бесконечности, то есть он имеет некоторое конечное значение. Но я хочу также рассмотреть интеграл, который я назову  , который также определен как интеграл от минус бесконечности до бесконечности но от абсолютного значения
, который также определен как интеграл от минус бесконечности до бесконечности но от абсолютного значения  :
:
Теперь немного терминологии. Если меньше бесконечности, если он сходится, то
меньше бесконечности, если он сходится, то  называется абсолютно сходящимся. Абсолютно сходящийся означает, что интеграл сходится, даже если использовать абсолютную величину функции. Наоборот, если
называется абсолютно сходящимся. Абсолютно сходящийся означает, что интеграл сходится, даже если использовать абсолютную величину функции. Наоборот, если  расходится, но при этом
расходится, но при этом  сходится, то
сходится, то  называется условно сходящимся. Таким образом, если интеграл функции сходится, но интеграл абсолютного значения этой же функции не сходится, то такой случай называется условной сходимостью.
называется условно сходящимся. Таким образом, если интеграл функции сходится, но интеграл абсолютного значения этой же функции не сходится, то такой случай называется условной сходимостью.
Причина такого разделения, заключается в том, что условно сходящиеся интегралы очень опасны. Они опасны тем, что недостаточно хорошо определены. Можно получить любое значение, которое мы захотим, складывая подынтегральную функцию в различном порядке. До тех пор, пока мы придерживаемся определенного порядка, который подразумевается в символе интеграла, мы получаем уникальный ответ. Но, если, например, мы просто переместим начало интегрирования, мы можем получить другой ответ. Обычно мы такого не ожидаем. Обычно мы просто интегрируем вдоль числовой линии, неважно, с какого места мы начинаем вычислять интеграл. Таким образом, результат становится гораздо менее определенными, когда мы работаем с условно сходящимися интегралами.
Прежде чем перейти к конкретному интегралу, который нас интересует, с помощью которого мы попытаемся сложить гравитационные силы бесконечного распределения вещества, я приведу пример очень простой функции, которая иллюстрирует эту неоднозначность, когда интеграл сходится, но не абсолютно сходится. Можно получить любой ответ, какой мы захотим, складывая части интеграла в разном порядке. Пример, который я рассмотрю, будет функцией f(x), которая равна +1, если x>0 и -1, если x<0. Я не указываю чему она равна, если x=0, при интегрировании это не имеет значения. Единственная точка не имеет значения. Можно взять любое значение для функции при x=0, это ничего не изменит.
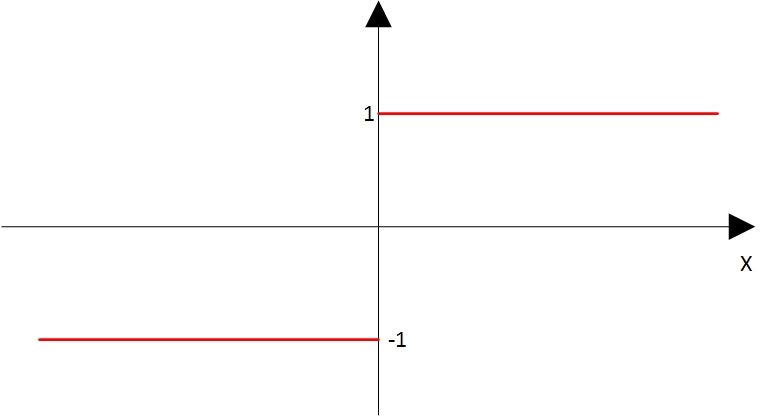
Если мы интегрируем ее симметрично, следуя определению того, что мы подразумеваем под интегрированием от минус бесконечности до бесконечности, мы получаем полное сокращение.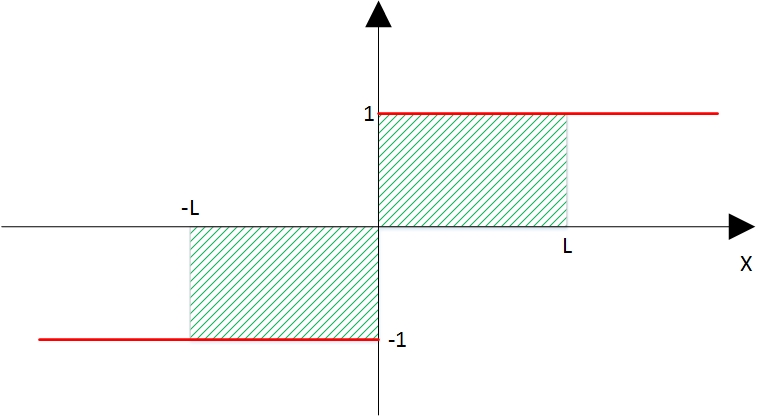
Когда мы интегрируем от до
до  , мы получаем ноль, потому что происходит полное сокращение между отрицательными частями и положительными частями интеграла. Тогда, если взять предел, когда
, мы получаем ноль, потому что происходит полное сокращение между отрицательными частями и положительными частями интеграла. Тогда, если взять предел, когда  стремится к бесконечности, предел нуля будет равен нулю. В этом утверждении нет никакой неоднозначности.
стремится к бесконечности, предел нуля будет равен нулю. В этом утверждении нет никакой неоднозначности.
Таким образом, складывая части интеграла в указанном порядке мы получаем интеграл, который равен нулю. Но результат зависит от того, в каком порядке мы складываем эти части. В частности, если просто изменить начало интегрирования, начиная двигаться в стороны от нового начала, мы получим другой ответ. Давайте опять рассмотрим предел, когда стремится к бесконечности, но вместо интегрирования от
стремится к бесконечности, но вместо интегрирования от  до
до  , мы будем интегрировать от
, мы будем интегрировать от  до
до  .
.
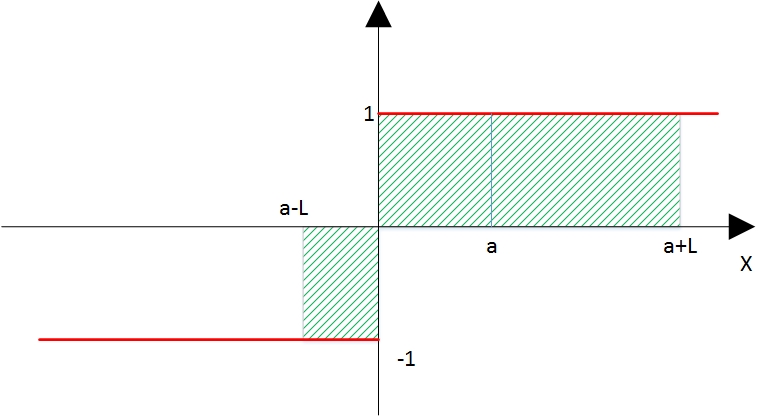
Это на самом деле тот же интеграл, мы просто сдвинули вправо наше начало интегрирования. В частном случае равно нулю, и мы получаем, то же, что и раньше, но, если
равно нулю, и мы получаем, то же, что и раньше, но, если  не равно нулю, это означает, что наш интеграл вычисляется, начиная от
не равно нулю, это означает, что наш интеграл вычисляется, начиная от  , а не от
, а не от  .
.
Сначала мы должны вычислить интеграл от до
до  , а затем взять предел, когда
, а затем взять предел, когда  стремиться к бесконечности, и посмотреть, что мы получим.
стремиться к бесконечности, и посмотреть, что мы получим.
Легко понять, что мы получим. Как только становится больше
становится больше  , ответ больше не меняется при увеличении
, ответ больше не меняется при увеличении  . Когда мы увеличиваем
. Когда мы увеличиваем  , у нас добавляется некоторая отрицательная часть слева, и такая же положительная справа, и они нейтрализуют друг друга. Когда
, у нас добавляется некоторая отрицательная часть слева, и такая же положительная справа, и они нейтрализуют друг друга. Когда  , интеграл будет от 0 до 2
, интеграл будет от 0 до 2 . В интеграле будут только положительные значения функции, промежуток интегрирования будет равен 2
. В интеграле будут только положительные значения функции, промежуток интегрирования будет равен 2 , это означает, что интеграл будет равен 2
, это означает, что интеграл будет равен 2 . Для любых больших значений
. Для любых больших значений  интеграл получится тем же самым, поскольку, при увеличении
интеграл получится тем же самым, поскольку, при увеличении  , как я уже сказал, мы просто сокращаем добавление положительных значений справа и отрицательных слева. Поэтому предел при таком интегрировании имеет вполне определенное значение, которое равно 2
, как я уже сказал, мы просто сокращаем добавление положительных значений справа и отрицательных слева. Поэтому предел при таком интегрировании имеет вполне определенное значение, которое равно 2 .
.
 – это число, с которого мы начали интегрирование, поэтому оно может быть каким угодно. Мы можем выбрать
– это число, с которого мы начали интегрирование, поэтому оно может быть каким угодно. Мы можем выбрать  каким хотим. Таким образом, мы можем получить любой ответ, который мы хотим, если мы можем добавлять части интеграла в произвольном порядке. Это фундаментальная неопределенность условно сходящихся интегралов. Мы увидим, что попытка сложить силы, действующие на частицу в бесконечном распределении массы, является именно таким условно сходящимся интегралом. Поэтому мы можем получить любой ответ, который захотим, и он не будет ничего значить, если только не проделывать все очень аккуратно.
каким хотим. Таким образом, мы можем получить любой ответ, который мы хотим, если мы можем добавлять части интеграла в произвольном порядке. Это фундаментальная неопределенность условно сходящихся интегралов. Мы увидим, что попытка сложить силы, действующие на частицу в бесконечном распределении массы, является именно таким условно сходящимся интегралом. Поэтому мы можем получить любой ответ, который захотим, и он не будет ничего значить, если только не проделывать все очень аккуратно.
Теперь я хочу вычислить силу, действующую на какую-либо частицу в бесконечном распределении вещества и показать, что я могу получить разные ответы, в зависимости от того, в каком порядке я буду складывать гравитационные силы. В каждом примере я буду складывать силы в определенном порядке, и получу определенный ответ, однако я получу разные ответы, в зависимости от того, какой порядок сложения я выберу.
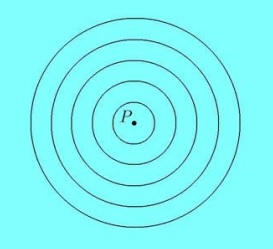
Давайте попытаемся вычислить гравитационную силу в некоторой точке в бесконечном распределении вещества. Вещество заполняет слайд, и все пространство, до бесконечности. Мы будем складывать гравитационный вклад всего этого вещества в определенном порядке.
в бесконечном распределении вещества. Вещество заполняет слайд, и все пространство, до бесконечности. Мы будем складывать гравитационный вклад всего этого вещества в определенном порядке.
В нашем первом расчете, мы сложим гравитационные силы от вещества, расположенного в концентрических оболочках с центром в точке . Cначала мы возьмем самую внутреннюю оболочку, затем вторую оболочку, третью оболочку, и т.д. идущие все дальше от центра. В этом случае легко понять, что сила, действующая на точку
. Cначала мы возьмем самую внутреннюю оболочку, затем вторую оболочку, третью оболочку, и т.д. идущие все дальше от центра. В этом случае легко понять, что сила, действующая на точку  , вычисленная в таком порядке, равна 0, поскольку для каждой оболочки
, вычисленная в таком порядке, равна 0, поскольку для каждой оболочки  находится в центре, и из соображения симметрии силы должны компенсироваться. На самом деле, известно, и мы вскоре воспользуемся этим фактом, что гравитационное поле оболочки внутри оболочки равно нулю. Это доказал еще Ньютон. А вне оболочки гравитационное поле выглядит точно так же, как если бы все вещество оболочки было сосредоточено в ее центре. Ясно, что в данном случае гравитационная сила в точке
находится в центре, и из соображения симметрии силы должны компенсироваться. На самом деле, известно, и мы вскоре воспользуемся этим фактом, что гравитационное поле оболочки внутри оболочки равно нулю. Это доказал еще Ньютон. А вне оболочки гравитационное поле выглядит точно так же, как если бы все вещество оболочки было сосредоточено в ее центре. Ясно, что в данном случае гравитационная сила в точке  равна 0.
равна 0.

Теперь мы рассмотрим более сложный случай, в котором мы также вычислим гравитационную силу в точке . Но мы будем использовать сферические оболочки с центром вокруг другой точки,
. Но мы будем использовать сферические оболочки с центром вокруг другой точки,  . Теперь
. Теперь  определяет оболочки которые мы будем использовать для складывания сил. Мы также сложим силы от всех оболочек от нуля до бесконечности, т.е. сложим все силы в точке
определяет оболочки которые мы будем использовать для складывания сил. Мы также сложим силы от всех оболочек от нуля до бесконечности, т.е. сложим все силы в точке  от всего бесконечного распределения вещества. Но мы будем складывать эти силы в другом порядке, потому что мы будем брать по порядку оболочки с центром в
от всего бесконечного распределения вещества. Но мы будем складывать эти силы в другом порядке, потому что мы будем брать по порядку оболочки с центром в  . Сначала мы рассмотрим вклад затененной области, которая является всеми оболочками вокруг
. Сначала мы рассмотрим вклад затененной области, которая является всеми оболочками вокруг  , имеющими радиусы меньше, чем расстояние от
, имеющими радиусы меньше, чем расстояние от  до
до  . Для всех этих оболочек точка
. Для всех этих оболочек точка  лежит вне оболочки. Поэтому каждая оболочка действует точно так же, как точечная масса, равная общей массе оболочки, сосредоточенная в точке
лежит вне оболочки. Поэтому каждая оболочка действует точно так же, как точечная масса, равная общей массе оболочки, сосредоточенная в точке  , центре всех оболочек. Таким образом, вещество, которое находится в затененной области, дает вклад в силу в точке
, центре всех оболочек. Таким образом, вещество, которое находится в затененной области, дает вклад в силу в точке  , равный силе, которая создала бы затененная масса, если бы она вся была сосредоточена в точке
, равный силе, которая создала бы затененная масса, если бы она вся была сосредоточена в точке  .
.
С другой стороны, все остальные оболочки будут оболочками, для которых находится внутри.
находится внутри.  больше не находится в центре этих оболочек, но Ньютон выяснил, что это не имеет значения. Внутри сферической оболочки гравитационная сила равна нулю в любом месте, независимо от того, насколько оно близко к границе. Все силы от разных частей оболочки в точности компенсируются. Если приблизиться к границе, то можно предположить, что возникнет притяжение в сторону этой границы. Действительно, в этом случае сила притяжения к конкретной частице на этой границе становится сильнее, потому что она пропорциональна
больше не находится в центре этих оболочек, но Ньютон выяснил, что это не имеет значения. Внутри сферической оболочки гравитационная сила равна нулю в любом месте, независимо от того, насколько оно близко к границе. Все силы от разных частей оболочки в точности компенсируются. Если приблизиться к границе, то можно предположить, что возникнет притяжение в сторону этой границы. Действительно, в этом случае сила притяжения к конкретной частице на этой границе становится сильнее, потому что она пропорциональна  . Но по мере приближения к границе, все больше вещества оказывается с противоположенной стороны. И эти два эффекта полностью компенсируют друг друга. Кстати, то, что сила, действующая на частицу внутри оболочки равна нулю, легко доказать, используя закон Гаусса для гравитации.
. Но по мере приближения к границе, все больше вещества оказывается с противоположенной стороны. И эти два эффекта полностью компенсируют друг друга. Кстати, то, что сила, действующая на частицу внутри оболочки равна нулю, легко доказать, используя закон Гаусса для гравитации.
Поэтому внешние оболочки не дают никакого вклада. Мы выяснили, что сила в точке равна силе, создаваемой затененной массой. Гравитационное ускорение в точке
равна силе, создаваемой затененной массой. Гравитационное ускорение в точке  определяется простой формулой: оно равно G умноженной на общую массу затененной области, деленной на
определяется простой формулой: оно равно G умноженной на общую массу затененной области, деленной на  , где
, где  равно расстоянию между
равно расстоянию между  и
и  , и умноженной на единичный вектор, направленный от
, и умноженной на единичный вектор, направленный от  в сторону
в сторону  :
:
И это ненулевое значение. Таким образом, мы получаем нулевой или ненулевой результат в зависимости от того, в каком порядке мы складываем силы от нашего бесконечного распределения вещества. Кроме того, мы можем получить любой ответ, потому что можем выбрать каким угодно. Ответ зависит от
каким угодно. Ответ зависит от  и становится сколь угодно большим, по мере увеличения
и становится сколь угодно большим, по мере увеличения  . Может показаться, что ответ уменьшается при увеличении
. Может показаться, что ответ уменьшается при увеличении  , но на самом деле он растет, поскольку масса
, но на самом деле он растет, поскольку масса  растет как
растет как  . Мы можем получить силу в любом направлении, выбрав
. Мы можем получить силу в любом направлении, выбрав  в нужной стороне от
в нужной стороне от  . Мы, действительно, можем получить любой ответ, используя такой способ сложения сил.
. Мы, действительно, можем получить любой ответ, используя такой способ сложения сил.
Проблема состоит в том, что этих оболочек на самом деле не существует. Мы просто мысленно работаем с этими оболочками. Вещество равномерно распределено и нет никаких оболочек. Оболочки являются чисто мысленными объектами, которые не должны влиять на ответ. Они только определяют порядок, в котором мы суммируем гравитационные силы.
Вашему вниманию предлагается перевод пятой лекции: «Космологическое красное смещение и динамика однородной расширяющейся вселенной, часть 1».
Сегодня мы закончим рассмотрение кинематики однородно расширяющейся вселенной, которую мы обсуждали в прошлый раз. Единственный вопрос из этой темы, который мы еще не затрагивали — это космологическое красное смещение. Затем мы перейдем к динамике однородного расширения — каким образом гравитация влияет на расширение вселенной. Это будет основной темой сегодняшней и нескольких следующих лекций.
Космологическое время
Напомню, что в конце последней лекции речь шла о синхронизации часов в системе координат, которую мы будем использовать для описания однородно расширяющейся вселенной. Вспомним, что мы ввели сопутствующие координаты, которые расширяются вместе со вселенной. Мы будем предполагать, что вселенная совершенно однородна и изотропна, и все объекты покоятся в этой системе координат.
В реальной вселенной имеется некоторое движение вещества относительно этой системы координат, потому что вселенная не совсем однородна. Но сейчас мы будем работать с приближением, в котором наша модельная вселенная абсолютно однородна и все вещество покоится относительно расширяющейся системы координат.
Теперь вспомним, как мы определили космологическое время на прошлой лекции. Представим себе, что в каждой точке вселенной имеются часы, находящиеся в покое относительно вещества, а значит и расширяющейся сопутствующей системы координат. Все такие часы измеряют локальное время, и мы хотим договориться о их синхронизации. В прошлый раз мы выяснили, что можем синхронизировать часы, если имеются какие-нибудь космологические явления, которые можно увидеть из любой точки вселенной, и которые меняются со временем. Мы привели два примера: один — изменение постоянной Хаббла, которую можно измерить локально и договориться установить свои часы на ноль, когда постоянная Хаббла примет определенное значение.
Второй пример — температура космического микроволнового фонового излучения. В нашей модельной вселенной можно договориться установить свои часы на ноль, когда температура космического фонового излучения достигнет 5 градусов или любого заданного числа. Если имеются подобные явления, а они есть в нашей вселенной, то можно синхронизировать все часы. Важно понимать, что как только часы будут однажды синхронизированы, они останутся синхронизированными вследствие нашего предположения об однородности. То есть, если все договорятся, что температура космического фонового излучения в нулевое время равна 10 градусам, и все подождут 15 минут, то все увидят одно и то же падение температуры в течение этого промежутка времени, иначе это было бы нарушением нашей гипотезы об абсолютной однородности.
СТУДЕНТ: Верно ли, что температура фонового излучения одинакова для всех инерциальных наблюдателей?
ПРЕПОДАВАТЕЛЬ: Она не совсем одинакова для разных инерциальных наблюдателей. Она одинакова для привилегированного класса наблюдателей, которые находятся в покое относительно усредненного распределения вещества и, значит, относительно сопутствующей системы координат. Если вы начнете перемещаться через космическое фоновое излучение, то вы больше не будете видеть равномерное распределение температуры. Вы увидите излучение более горячее в одном направлении и более холодное в обратном. На самом деле, как я уже упоминал, мы видим этот эффект в нашей реальной вселенной. Мы, по-видимому, движемся относительно космического фонового излучения, примерно с 1/1000 от скорости света. Так что температура излучения не инвариантна по отношению к движению наблюдателя.
Можно задаться другим вопросом – одинакова ли температура фонового излучения в различных местах видимой вселенной? Насколько мы можем судить, да. Существует прямой способ измерения температуры фонового излучения, о котором мы, возможно, поговорим позже в курсе, при помощи наблюдения за определенными спектральными линиями в далеких галактиках. В некоторых галактиках, где видны эти линии, можно напрямую измерять температуру космического микроволнового фонового излучения. В нашей модели мы предполагаем полную однородность, что все везде одинаково. Хотя однородность в реальной вселенной не полная, есть веские доказательства приближенной однородности нашей вселенной.
СТУДЕНТ: Если некоторые наблюдатели живут рядом с черными дырами, повлияет ли это на синхронизацию часов для таких наблюдателей?
ПРЕПОДАВАТЕЛЬ: конечно, повлияет. Можно космологически синхронизировать часы, только предполагая, что вселенная абсолютно однородна. Как только появляются неоднородности, такие как черные дыры, или даже просто звезды, подобные Солнцу, они создают отклонения, которые препятствуют синхронизации часов друг с другом. Как только появляется концентрация массы, однородность становится лишь приблизительной. Но эти отклонения невелики. Отклонения, возникающие из-за Солнца, составляют порядка одной миллионной. Поэтому, в очень хорошем приближении вселенная описывается нашей однородной моделью. Хотя, если очень приблизиться к одной из сверхмассивных черных дыр, находящихся в центрах галактик, окажется, что она оказывает очень сильное влияние на ход ваших часов.
Космологическое красное смещение
Следующая тема, как я и обещал — космологическое красное смещение. В третьей лекции, мы говорили о доплеровском сдвиге для звуковых волн и о релятивистском доплеровском сдвиге для световых волн, с учетом специальной теории относительности. Однако, космология не полностью описывается специальной теорией относительности, хотя специальная теория относительности используется для описания локальных событий в космологии. Специальная теория относительности не включает в себя эффекты гравитации, а в глобальном масштабе эффекты гравитации очень важны для космологии. Поэтому специальной теории относительности недостаточно, чтобы понять многие свойства вселенной, включая космологическое красное смещение. Однако оказывается, что есть способ описания космологического красного смещения, который объясняет его еще проще, чем специальная теория относительности. Сначала я опишу его, а затем мы поговорим о том, как этот очень простой на вид результат соотносится с выводом специальной теории относительности, который также должен быть правильным, по крайней мере, локально.
Итак, предположим, что мы смотрим на далекую галактику, и свет излучается источником, находящимся в этой галактике. Мы хотим понять, какова зависимость между частотой света при излучении, и частотой, которую мы увидим при получения света.
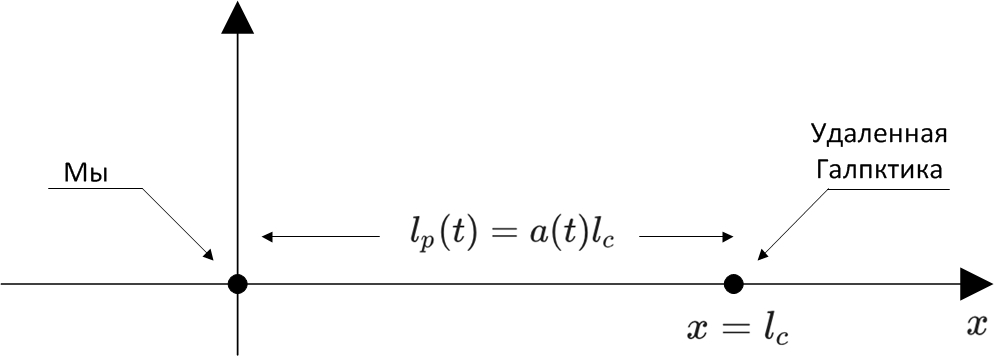
Чтобы представить себе эту ситуацию, давайте введем систему координат,
Предположим теперь, что галактика излучает световую волну, и мы пытаемся определить расстояние между гребнями волны, которое равно длине волны. Поскольку нас будут интересовать только гребни, мы просто представим, что каждый гребень — это импульс, и то, что происходит между ними, нас не интересует. Мы будем следить за последовательными световыми импульсами, излучаемыми галактикой.
Важно, что мы знаем для нашей модели, как распространяются световые волны в сопутствующей системе координат. Если
Масштабный фактор здесь играет роль преобразования метров в деления.
Важная особенность этого уравнения, заключается в том, что скорость света в сопутствующей системе координат зависит от времени, но не зависит от
Это означает следующее. Сопутствующая скорость импульсов может меняться со временем, но до тех пор, пока они оба двигаются с одинаковой сопутствующей скоростью, в любой момент времени они будут находиться ровно на одном и том же расстоянии друг от друга в сопутствующей системе координат.
То, что
Длина волны связана с периодом волны отношением
Таким образом, отношение длин волн — это просто число раз, в которое вселенная растянулась. Оно равно отношению масштабных факторов в начальное и конечное время. Мы определяли красное смещение при помощи периода волны. Отношение периодов, или отношение длин волн, или отношение масштабных факторов, равняется 1 + z.
Связь космологического красного смещения со специальной теорией относительности
Каким образом космологическое красное смещение связано с красным смещением специальной теории относительности, формулу для которого мы вывели ранее? Наш результат отличается в двух отношениях от расчета, который мы сделали на третей лекции. Первая причина, которая важна для нас, это то, что космологический расчет учитывает эффекты, которые не были приняты во внимание предыдущими расчетами. В частности, несмотря на то, что мы получили ответ при помощи очень простого кинематического аргумента, в котором, на первый взгляд, практически нет никакой математики, он на самом деле очень сильный, поскольку он учитывает не только специальную теорию относительности, но и общую теорию относительности. Он включает в себя все эффекты гравитации. Гравитация не влияет на факт, что сопутствующая скорость света равна
Поэтому, когда мы учитываем гравитацию, это соотношение продолжает сохраняться, а это было единственное, что мы использовали, так что гравитация не может повлиять на ответ. Не упустили ли мы что-нибудь из специальной теории относительности? Я не учел замедление времени, которое имело решающее значение для нашего релятивистского вычисления красного смещения.
Сделал ли я ошибку? Нужно ли куда-нибудь добавить замедление времени? На самом деле, нет. У нас было двое часов, задействованных в нашем расчете: часы в галактике и наши часы, которые мы использовали для измерения периода излучения и периода приема. Но оба этих часов находятся в покое относительно локального вещества, даже несмотря на то, что они движутся относительно друг друга. Поэтому, по определению, они измеряют космологическое время. Космологическое время — это очень своеобразный вид времени, это не время в какой-либо инерциальной системе. Часы двигаются относительно друг друга, поэтому, если бы мы определяли время в инерционной системе, такие часы никогда не могли бы быть синхронизированы и время бы на них не совпадало.
Но в системе космологического времени, они показывают одно и то же время. Поскольку каждые часы находятся в покое относительно локального вещества, они измеряют
Таким образом, полученный результат, каким бы простым он ни казался, на самом деле полностью охватывает эффекты как специальной теории относительности, так и гравитации. Позвольте заметить, что не очевидно, где здесь гравитация. Я сказал вам, что результат включает в себя все эффекты гравитации. Где же спрятана гравитация? Я хочу задать этот вопрос вам. Каким образом гравитация влияет на вычисления, несмотря на то, что я не упоминал гравитацию, когда делал расчет?
СТУДЕНТ: Через масштабный фактор.
ПРЕПОДАВАТЕЛЬ: Правильно, через масштабный фактор. Мы еще не говорили о том, как меняется
Другое важное различие между этими двумя вычислениями — это используемые в ответе переменные. На один и тот же вопрос может быть несколько разных ответов, в зависимости от того, какие используются переменные. В данном случае мы выражаем красное смещение
Что будет, если мы попытаемся сравнить ответы, которые мы получили для релятивистского и для космологического красного смещения? Имеется только один случай, в котором их правомерно сравнивать. Поскольку расчет, который мы только что сделали, включает эффекты гравитации, а расчет при помощи специальной теории относительности не включает эффектов гравитации, единственным случаем, при котором мы можем их сравнить и убедиться, что они совпадают, является случай, когда гравитация пренебрежимо мала.
Можно рассматривать космологическую модель, где гравитация мала, в этом нет никакого противоречия. Если гравитация незначительна, как будет вести себя
Тогда для этого частного случая, наши два расчета должны совпасть. Вы можете это сами проверить. Это не так просто, для этого понадобится понимание взаимосвязи между двумя системами координат. Ответ специальной теории относительности дается в инерциальной системе координат, которая при наличии гравитации вообще не существует. Она связана с расширяющейся системой координат сложным образом, из-за замедления времени и Лоренцева сокращения, связанных с движением, которое происходит в расширяющейся вселенной.
Вам нужно будет выяснить взаимосвязь между этими двумя системами координат. Когда вы это сделаете, и сравните ответы, то обнаружите, что они действительно точно совпадают. Все это прекрасно согласуется со специальной теорией относительности, в частном случае, когда гравитация отсутствует.
Ньютон и статичная вселенная
Мы обсудили все, что я хотел рассказать о кинематике однородно расширяющейся вселенной, теперь мы готовы перейти к динамике. Нам нужно выяснить, каким образом гравитация влияет на вселенную, чтобы иметь возможность вычислить, как
Этот вопрос, в некотором смысле, восходит к Исааку Ньютону. Хочу заметить, что одна из интересных вещей в космологии заключается в том, что, если посмотреть на историю космологии, многие великие физики допускали большие ошибки, пытаясь проанализировать космологические вопросы. Сегодня мы обсудим одну из ошибок Ньютона. Даже такие великие физики, как Ньютон, могли совершать глупые ошибки. Он действительно совершил глупую ошибку, анализируя космологические последствия своей собственной теории гравитации.
Ньютон, как и все до Хаббла считал, что вселенная статична. Он представлял вселенную как статичное распределение звезд, разбросанных в пространстве. В начале своей карьеры, насколько я знаю историю, он предполагал, что распределение звезд было конечным в бесконечном пространстве. Но в какой-то момент он понял, что если имеется конечное распределение массы в пустом пространстве, а все вещество притягивается друг к другу с силой притяжения обратно пропорциональной квадрату расстояния, о которой он знал, поскольку он открыл ее, в результате все должно сжаться в точку. Он решил, что его предположение не работает, но все равно он был уверен, что вселенная статична, поскольку все выглядело статично, звезды никуда не двигались.
Поэтому он задался вопросом, что можно изменить, и решил, что вместо того, чтобы предполагать, что звезды образуют конечное распределение, лучше предположить, что они распределены бесконечно в пространстве. Он рассуждал следующим образом, а это как раз и является заблуждением, что если звезды заполняют бесконечное пространство, то, даже если все они будут притягивать друг друга, у них не будет предпочтительного направления для движения. Поскольку у них не будет предпочтительного направления для движения, потому что на них действует притяжение со всех сторон, они остаются на месте. Таким образом, он полагал, что бесконечное, равномерное распределение вещества будет стабильным, что не будет никаких гравитационных сил, возникающих в таком бесконечном распределении массы.
Он, по-видимому, слышал разные аргументы в пользу этого. Один из аргументов, что бесконечное распределение будет стабильным, был аргумент, что на частицу действует бесконечная сила тянущая ее вправо и бесконечная сила, тянущая ее влево. Так как обе они бесконечны, они нейтрализуют друг друга. Ньютон не принял этот аргумент. Он был достаточно искушенным, чтобы понять, что бесконечность минус бесконечность не обязательно равна нулю. Тем не менее, Ньютон был убежден, что бесконечное распределение массы будет стабильным.
Аргумент, который убедил его, был не бесконечностью вещества с каждой стороны, а симметрией. Аргумент, который он принимал, заключался в том, что, если посмотреть на любую точку этого бесконечного распределения, если посмотреть вокруг этой точки, все направления будут выглядеть одинаково, с веществом, простирающейся до бесконечности, и поэтому не будет направления, в котором сила должна действовать на любую конкретную частицу. А если у силы нет направления, она должна быть равна нулю. Это был аргумент, который принимал Ньютон.
Сейчас мы обсудим это более подробно и попытаемся понять, как современные ученые относятся к этому аргументу. Кстати, хочу упомянуть исторический факт. Аргумент Ньютона, насколько мне известно, не подвергался сомнению ни у кого в течение сотен лет, вплоть до Альберта Эйнштейна. Альберт Эйнштейн, пытаясь описать космологию при помощи своей новой общей теории относительности, был первым человеком, осознавшим, что даже если у вас бесконечное распределение массы, она сколлапсирует. Эйнштейн понял, что то же самое произойдет и в Ньютоновской физике, это не особенность общей теории относительности. Просто исторически потребовалось создание общей теории относительности, чтобы заставить людей переосмыслить и понять, что Ньютон был неправ.
Невозможность существования статичной вселенной
Трудность попытки проанализировать проблему так, как это сделал Ньютон, заключается в том, что Ньютон рассматривал гравитацию как силу, действующую на расстоянии. Если у нас есть два объекта, расположенных на расстоянии
Первую я опишу по аналогии с законом Кулона. Закон Кулона действительно такой же, как закон силы тяжести. Закон Кулона гласит, что любая заряженная частица создает электрическое поле, которое равно заряду, деленному на расстояние в квадрате и умноженному на единичный вектор, направленный от заряда.
Это закон Кулона. Иногда в нем стоит константа, в зависимости от того, в каких единицах измеряется
Как известно, из закона Кулона можно получить закон Гаусса. Если закон Кулона верен, то можно однозначно сказать, чему равен интеграл потока электрического поля по любой замкнутой поверхности. Он пропорционален общей сумме заряда внутри поверхности.
где
Можно записать закон тяготения Ньютона, почти так, как его сформулировал Ньютон. Можно выразить гравитационное ускорение на заданном расстоянии от объекта:
Это такой же закон обратных квадратов и похож на закон Кулона, за исключением константы в начале. Константа имеет противоположный знак, что важно в некоторых случаях, но не сейчас. Важным является то, что это уравнение может быть переформулировано как закон Гаусса, и оно называется законом гравитации Гаусса. Единственное, чем оно отличается – это константа впереди:
Теперь давайте возьмем однородное распределение вещества, которое рассматривал Ньютон. Ньютон утверждал, что можно взять однородное распределение вещества, заполняющее все бесконечное пространство, и оно будет статично, то есть не будет ускорения. Отсутствие ускорения на языке Ньютона означает, что
Просто ради интереса, я приведу вам еще один похожий аргумент, используя другую более современную формулировку Ньютоновской гравитации. Если вы ее не встречали и не понимаете, о чем я говорю, не беспокойтесь, это не так важно. Для тех из вас, кто с ней знаком, я ее приведу. Другой способ формулировки Ньютоновской гравитации — ввести гравитационный потенциал. Я буду использовать букву
Как только мы определили гравитационный потенциал, можно написать дифференциальную форму закона Гаусса, которая становится так называемым уравнением Пуассона. Оно утверждает, что
Это называется уравнением Пуассона. Если задана плотность массы, то можно найти гравитационный потенциал, затем можно вычислить его градиент, и найти
Если посмотреть на формулу градиента, то это вектор. Для нулевого вектора каждый из трех его компонентов должен быть равен нулю, и, следовательно, производная от
Условно сходящиеся интегралы
Итак, мы пришли к выводу, что Ньютон был неправ, но нам нужно более тщательно проанализировать аргумент Ньютона, чтобы понять, где именно он ошибся. Следующее, что я хочу обсудить, это неоднозначность, связанная со сложением Ньютоновских гравитационных сил для бесконечной вселенной. Я упомянул, что реальная проблема с вычислениями Ньютона заключается в том, что сумма, которую он вычислял, расходится, и нужно быть осторожным, при попытке ее вычисления.
Чтобы прояснить это, я хочу начать с примера интеграла, который дает неоднозначное значение. Я введу пару математических понятий. Давайте представим, что у нас есть некоторая произвольная функция
Мы обобщим ее на три измерения, что нас и интересует, но начнем с одной переменной. Если у нас есть функция
Именно такой интеграл получается при сложении всех гравитационных сил, действующих на тело. Теперь я хочу рассмотреть случай, когда
Мне нужно сначала более точно определить, что я имею в виду под
Нам нужно вычислить интеграл от
Теперь рассмотрим случай, когда это значение существует, когда
Теперь немного терминологии. Если
Причина такого разделения, заключается в том, что условно сходящиеся интегралы очень опасны. Они опасны тем, что недостаточно хорошо определены. Можно получить любое значение, которое мы захотим, складывая подынтегральную функцию в различном порядке. До тех пор, пока мы придерживаемся определенного порядка, который подразумевается в символе интеграла, мы получаем уникальный ответ. Но, если, например, мы просто переместим начало интегрирования, мы можем получить другой ответ. Обычно мы такого не ожидаем. Обычно мы просто интегрируем вдоль числовой линии, неважно, с какого места мы начинаем вычислять интеграл. Таким образом, результат становится гораздо менее определенными, когда мы работаем с условно сходящимися интегралами.
Прежде чем перейти к конкретному интегралу, который нас интересует, с помощью которого мы попытаемся сложить гравитационные силы бесконечного распределения вещества, я приведу пример очень простой функции, которая иллюстрирует эту неоднозначность, когда интеграл сходится, но не абсолютно сходится. Можно получить любой ответ, какой мы захотим, складывая части интеграла в разном порядке. Пример, который я рассмотрю, будет функцией f(x), которая равна +1, если x>0 и -1, если x<0. Я не указываю чему она равна, если x=0, при интегрировании это не имеет значения. Единственная точка не имеет значения. Можно взять любое значение для функции при x=0, это ничего не изменит.

Если мы интегрируем ее симметрично, следуя определению того, что мы подразумеваем под интегрированием от минус бесконечности до бесконечности, мы получаем полное сокращение.

Когда мы интегрируем от
Таким образом, складывая части интеграла в указанном порядке мы получаем интеграл, который равен нулю. Но результат зависит от того, в каком порядке мы складываем эти части. В частности, если просто изменить начало интегрирования, начиная двигаться в стороны от нового начала, мы получим другой ответ. Давайте опять рассмотрим предел, когда

Это на самом деле тот же интеграл, мы просто сдвинули вправо наше начало интегрирования. В частном случае
Сначала мы должны вычислить интеграл от
Легко понять, что мы получим. Как только
Проблема сложения гравитационных сил
Теперь я хочу вычислить силу, действующую на какую-либо частицу в бесконечном распределении вещества и показать, что я могу получить разные ответы, в зависимости от того, в каком порядке я буду складывать гравитационные силы. В каждом примере я буду складывать силы в определенном порядке, и получу определенный ответ, однако я получу разные ответы, в зависимости от того, какой порядок сложения я выберу.

Давайте попытаемся вычислить гравитационную силу в некоторой точке
В нашем первом расчете, мы сложим гравитационные силы от вещества, расположенного в концентрических оболочках с центром в точке

Теперь мы рассмотрим более сложный случай, в котором мы также вычислим гравитационную силу в точке
С другой стороны, все остальные оболочки будут оболочками, для которых
Поэтому внешние оболочки не дают никакого вклада. Мы выяснили, что сила в точке
И это ненулевое значение. Таким образом, мы получаем нулевой или ненулевой результат в зависимости от того, в каком порядке мы складываем силы от нашего бесконечного распределения вещества. Кроме того, мы можем получить любой ответ, потому что можем выбрать
Проблема состоит в том, что этих оболочек на самом деле не существует. Мы просто мысленно работаем с этими оболочками. Вещество равномерно распределено и нет никаких оболочек. Оболочки являются чисто мысленными объектами, которые не должны влиять на ответ. Они только определяют порядок, в котором мы суммируем гравитационные силы.