Мечта всякого коллекционера – механический калькулятор Curta – устройство, которое до сих пор сохраняет статус культового изобретения. Вплоть до появления электронных вычислительных устройств в 70-е годы прошлого века, этот похожий на старую кофемолку прибор считался самым удобным карманным калькулятором. Изюминка устройства в том, что оно было полностью механическим. Ни тебе электричества, ни батарей, только несколько сот крошечных деталей.

Изобретатель этого аппарата Курт Херцштарк (1902-1988) — сын венского бизнесмена. Херцштарк-старший руководил предприятием по производству высокоточных механических устройств, на котором Курт и сделал свои первые шаги в механике. В то время уже существовали карманные калькуляторы, но они могли только складывать и вычитать. Херцштарк же мечтал создать арифмометр, способный выполнять все четыре действия. Зимой 1938 года был построен первый полноценный образец, однако массовое производство не началось: помешала война.

В 1943 году Курт Херцштак был арестован по обвинению в «пособничестве евреям», а также «порочных связях с арийскими женщинами». После долгих мытарств по тюрьмам он оказался в концлагере в Бухенвальде.
Узнав, кто попал к нему в руки, начальник лагеря был очень доволен. Изобретение Херцштарка показалось отличным подарком для фюрера. Курту выдали кульман и приказали сделать чертеж по памяти. Работая и днем и ночью, изобретатель восстановил схему калькулятора. Однако Гитлер свой презент так и не получил: в 1945 году всех пленников лагеря освободили американские войска.

С полным набором чертежей Херцштарк вышел на свободу. Князь Лихтенштейн разрешил ему построить фабрику и в 1947 году началось серийное производство устройства. Сначала калькулятор хотели назвать «Лилипут», но название не прижилось. На торговой ярмарке 1948 года в Базеле кто-то из участников обронил: «Эта машина — дочь господина Херцштарка. Если отца зовут Курт, то дочь нужно назвать Куртой».

Curta — самый компактный из всех механических карманных калькуляторов, которые когда-либо были придуманы. Аппарат весит всего 100 граммов. А вот работает он совсем по-взрослому. Первые Curta были 11-разрядными (Curta I), в 1954 году появилась 15-разрядная модель (Curta II). Добавим, что эта чудо-машина умела вычислять квадратные корни и позволяла умножать на девять всего двумя поворотами рукоятки.
До 1947 года основой всех механических калькуляторов служили ступенчатый барабан (по примеру Лейбница) или цевочное колесо (придуманное Однером). Курт Херцштарк предложил нечто новое – так называемый дополненный ступенчатый барабан.
«Дополненный» барабан упрощает работу, поскольку позволяет выполнять разные арифметические действия по одному алгоритму. Например, вычитание превратить в сложение. Каким образом? Поясним примером:
Допустим, нам надо решить такую задачу: 219875 — 5789 = ?
Предположим, у нас есть 11-разрядный калькулятор
..00 000 219 875 — Уменьшаемое
..00 000 005 789 — Вычитаемое
..99 999 994 210 — Дополняем каждый разряд вычитаемого до девяти
100 000 214 085 — Складываем строки 1 и 3
Поскольку цифра 1 лежит вне 11- разрядного диапазона, ее просто отсекаем. Итоговый
результат получился короче на один разряд, поэтому прибавляем единицу к значению низшего разряда.
..00 000 214 086 — Верный ответ
Современные калькуляторы выполняют операции вычитания по этому же алгоритму. Разница состоит лишь в том, что электронные устройства используют двоичную систему счисления.
Ну и несколько картинок напоследок:

Curta I с круглыми установочными ручками. Справа – каретка. Ее белая часть – это шестизначный счетчик оборотов, темная часть – 11-разрядное окно результата.

Деталь классического калькулятора со ступенчатым барабаном. Четко видны четыре передачи ступенчатых барабанов, при помощи которых задается число (разряды возрастают слева направо). Нужное число задается при помощи ползуна.
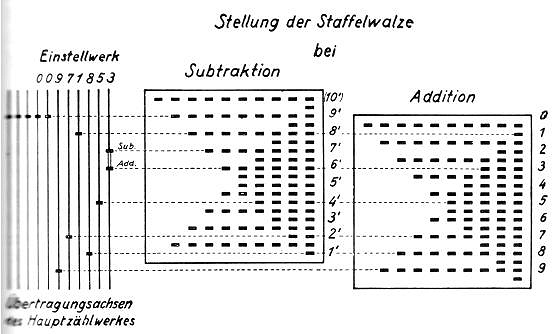
Схема, объясняющая принцип работы дополняющего ступенчатого барабана Херцштарка (по ссылке 3D-визуализация).

Слева – ранний 11-разрядный Curta I, рукоятка которого помещена в положение для выполнения вычитания. Справа – более поздний Curta I, рукоятка которого помещена в положение для выполнения сложения. Сдвиг по вертикали – всего 3 мм.
P.S. Кстати, в работе Curta издавала звук, похожий на урчание сытого кота.
P.P.S. Curta – это единственный арифмометр, когда-либо запечатленный на почтовых марках (Лихтенштейн).
P.P.P.S.Топик уже постили в феврале, но по поиску «Хабра» я его, к сожалению, не нашел. С другой стороны, нет такой избитой темы, которую нельзя пнуть еще раз.
via: vcalc.net

Изобретатель этого аппарата Курт Херцштарк (1902-1988) — сын венского бизнесмена. Херцштарк-старший руководил предприятием по производству высокоточных механических устройств, на котором Курт и сделал свои первые шаги в механике. В то время уже существовали карманные калькуляторы, но они могли только складывать и вычитать. Херцштарк же мечтал создать арифмометр, способный выполнять все четыре действия. Зимой 1938 года был построен первый полноценный образец, однако массовое производство не началось: помешала война.

В 1943 году Курт Херцштак был арестован по обвинению в «пособничестве евреям», а также «порочных связях с арийскими женщинами». После долгих мытарств по тюрьмам он оказался в концлагере в Бухенвальде.
Узнав, кто попал к нему в руки, начальник лагеря был очень доволен. Изобретение Херцштарка показалось отличным подарком для фюрера. Курту выдали кульман и приказали сделать чертеж по памяти. Работая и днем и ночью, изобретатель восстановил схему калькулятора. Однако Гитлер свой презент так и не получил: в 1945 году всех пленников лагеря освободили американские войска.

С полным набором чертежей Херцштарк вышел на свободу. Князь Лихтенштейн разрешил ему построить фабрику и в 1947 году началось серийное производство устройства. Сначала калькулятор хотели назвать «Лилипут», но название не прижилось. На торговой ярмарке 1948 года в Базеле кто-то из участников обронил: «Эта машина — дочь господина Херцштарка. Если отца зовут Курт, то дочь нужно назвать Куртой».

Curta — самый компактный из всех механических карманных калькуляторов, которые когда-либо были придуманы. Аппарат весит всего 100 граммов. А вот работает он совсем по-взрослому. Первые Curta были 11-разрядными (Curta I), в 1954 году появилась 15-разрядная модель (Curta II). Добавим, что эта чудо-машина умела вычислять квадратные корни и позволяла умножать на девять всего двумя поворотами рукоятки.
До 1947 года основой всех механических калькуляторов служили ступенчатый барабан (по примеру Лейбница) или цевочное колесо (придуманное Однером). Курт Херцштарк предложил нечто новое – так называемый дополненный ступенчатый барабан.
«Дополненный» барабан упрощает работу, поскольку позволяет выполнять разные арифметические действия по одному алгоритму. Например, вычитание превратить в сложение. Каким образом? Поясним примером:
Допустим, нам надо решить такую задачу: 219875 — 5789 = ?
Предположим, у нас есть 11-разрядный калькулятор
..00 000 219 875 — Уменьшаемое
..00 000 005 789 — Вычитаемое
..99 999 994 210 — Дополняем каждый разряд вычитаемого до девяти
100 000 214 085 — Складываем строки 1 и 3
Поскольку цифра 1 лежит вне 11- разрядного диапазона, ее просто отсекаем. Итоговый
результат получился короче на один разряд, поэтому прибавляем единицу к значению низшего разряда.
..00 000 214 086 — Верный ответ
Современные калькуляторы выполняют операции вычитания по этому же алгоритму. Разница состоит лишь в том, что электронные устройства используют двоичную систему счисления.
Ну и несколько картинок напоследок:

Curta I с круглыми установочными ручками. Справа – каретка. Ее белая часть – это шестизначный счетчик оборотов, темная часть – 11-разрядное окно результата.

Деталь классического калькулятора со ступенчатым барабаном. Четко видны четыре передачи ступенчатых барабанов, при помощи которых задается число (разряды возрастают слева направо). Нужное число задается при помощи ползуна.

Схема, объясняющая принцип работы дополняющего ступенчатого барабана Херцштарка (по ссылке 3D-визуализация).

Слева – ранний 11-разрядный Curta I, рукоятка которого помещена в положение для выполнения вычитания. Справа – более поздний Curta I, рукоятка которого помещена в положение для выполнения сложения. Сдвиг по вертикали – всего 3 мм.
P.S. Кстати, в работе Curta издавала звук, похожий на урчание сытого кота.
P.P.S. Curta – это единственный арифмометр, когда-либо запечатленный на почтовых марках (Лихтенштейн).
P.P.P.S.Топик уже постили в феврале, но по поиску «Хабра» я его, к сожалению, не нашел. С другой стороны, нет такой избитой темы, которую нельзя пнуть еще раз.
via: vcalc.net