Нечем заняться? тогда может быть просто написать 3D Console Software Rendering?
Добро пожаловать под кат!

Сегодня я расскажу вам от том, как написать простейший software 3D renderer.
Без всяких оптимизаций (что характерно для программ такого рода), т.к. моя главная цель — рассказать, как происходит 3D рендеринг, а не ускорение его работы.
Формат статьи не позволяет описать суть используемых алгоритмов и объяснять, почему, к примеру, матрицы преобразований выглядят так, а не иначе. В таких случаях я просто дам ключевые слова для поиска или ссылку и напишу, что оно должно делать. Прошу отнестись с пониманием :)
Итак, начнём:
В нашем случае простейший 3D рендерер будет включать в себя:
Опишу в общих чертах алгоритм рендеринга одного треугольника (таким образом, он будет повторяться для каждого треугольника, выводимого на экран).
ColorBuffer и ZBuffer в нашем случае просто 2 массива 80х25 (это для примера, конечно же, всё зависит от размера консоли). Первый будет хранить символы консоли и, если хотите, их цвет. Второй — значения глубины для каждого пикселя. Это может быть float или double — любой тип данных, являющийся числом с плавающей точкой. Я реализовал это в виде шаблонного класса, где параметр шаблона — это тип данных, хранящийся в массиве.
Алгоритм растеризации нужен для построении пиксельного треугольника из заданных трех точек на экране их координатами x,y,z; Чтобы это понять и осознать, рекомендую почитать ru.wikipedia.org/wiki/Алгоритм_Брезенхэма для растеризации линии и далее используйте его для растеризации теугольника: compgraphics.info/2D/triangle_rasterization.php
Есть разные алгоритмы для этих целей, используйте любой, который понравится. Главное, чтобы была реализована функциональность генерации всех точек треугольника/линии по заданным экранным координатам (т.е. у меня, например, это будет в диапазоне 0..79, 0..24).
Или можете взять тот, который реализован у меня — есть функция растеризации треугольника, которая использует функцию растеризации линии, которая вызывает функцию растеризации точки, которая выполняет z-test и выводит точку на экран. (иголка в яйце, яйцо в утке, и т.д.)
На скорость работы я не обращаю внимание, поскольку так легче проследить логику работы. У себя, разумеется, можно что-нибудь соптимизировать.
Итак, пусть у нас задана в трёхмерном пространстве точка с координатами x,y,z;
Я расскажу, как выполнить корректные преобразования Model-View-Projection для создания эффекта трёхмерности. Как я уже говорил, сначала мы делаем четырёхмерный вектор (x,y,z,1)
Самым первым выполняется преобразование Model. По сути это просто перенос/поворот/сжатие/растяжение или другое преобразование системы координат. Оно нужно для того, чтобы легко перемещать объект с течением времени — например у нас объект поворачивается на несколько град��сов вокруг оси Х каждые 10 мс. Соответственно, координаты модели мы храним как есть, а изменяем просто матрицу, задающую этот поворот.
Я приведу пример простейших матриц трёхмерного преобразования — перенос, поворот, сжатие.
Соответственно, для более сложных преобразований берите их композицию. Я представляю вектор как вектор-столбец и домножаю его на матрицу справа. Соответственно, если вам нужно сделать наоборот — транспонируйте матрицы и домножайте в другом порядке. Заметьте, что порядок перемножения самих матриц важен — если вы хотите повернуть объект и затем сделать перенос, то умножайте матрицу переноса на поворот и затем на координаты радиус-вектора точки. Итоговый вектор будет радиус-вектором преобразованной точки.
Примеры матриц:
Поворот вокруг других осей делается аналогично: просто подставьте соответствующую матрицу поворота в верхнюю левую 3х3 подматрицу
Поворот вокруг произвольной оси: в OpenGL существует функция, которой можно скормить угол поворота и направление оси (любое), а она сама сгенерирует матрицу поворота и домножит на неё.
Функция просто вычисляет матрицу поворота, поэтому я не буду её здесь описывать. Её можно написать самим, нагуглить (называется glRotate) или взять из моего исходника (я уже погуглил за вас:)
Далее выполн��ется преобразование View. Наверное проще всего это объяснить через понятие «камеры». Если Вы играли в трёхмерные игры, то наверняка представляете себе, что это — это точка, из которой вы смотрите на игровой мир и ориентация камеры в пространстве этого мира. Для этого нужно выполнять преобразования, обратные вышеуказанным. Например, если надо взглянуть на мир из точки (1,2,3), то нужно сделать перенос (-1,-2,-3). Это логично — представьте себе, что объект 3D-мира имеет координаты (a,b,c). Тогда его матрица модели будет соответствующая — перенос a,b,c. Если при этом камера смотрит на мир из той же точки, то матрица view будет иметь вид: перенос -a,-b,-c и в итоге при перемножении View*Model*(x,y,z,1) мы получим исходные координаты объекта — таким образом камера находится там же, где и объект.
Тут ещё должны быть повороты для задания ориентации камеры. Дабы не усложнять никому жизнь, скажу лишь — погуглите функцию gluLookAt (эта статья и так большая, думаю, не стоит постить сюда исходник) или возьмите мой исходник — там тоже есть эта функция. Она генерирует матрицу View для заданных координат позиции камеры, направления взгляда и вектора up (без этого вектора ориентация камеры, очевидно, неоднозначна).
Что за матрица в итоге получается? Представьте, что у вас есть некоторая исходная система координат и вы делаете перемещение/поворот и получаете другую систему координат. Это преобразование задаётся некоторой матрицей. Если начало новой системы координат совпадает с позицией камеры, ось 'z' направлена по направлению взгляда, а 'y' — вверх, то матрица преобразование View — это обратная матрица этого преобразования. Конечно же, обратную матрицу никто не ищет — просто для получения ViewMatrix сразу делаются обратные преобразования.
И, наконец, Projection. Матрица проекции выполняет преобразование координат из пирамиды видимости (Frustum) в единичный куб (с учетом перспективы), после чего точку уже легко вывести на экран.
Frustum — это как раз та часть мира, которая проецируется на экран. Она представляет из себя усечённую пирамиду с двумя треугольниками в основании.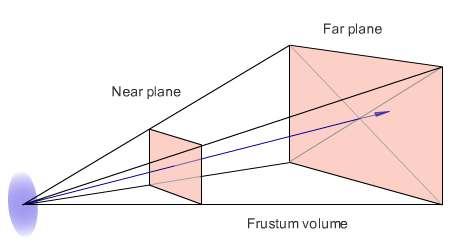
Я также не буду углубляться в объяснения об устройстве матрицы проекции, ясно, что она зависит от параметров znear, zfar (передняя и задняя плоскости отсечения), fovy (угол обзора по вертикали) и aspectratio (отношение ширины colorbuffer к высоте — для того, чтобы квадрат выглядел квадратом на прямоугольном экране, а не прямоугольником). Гуглите функцию gluPerspective или возьмите из моего исходника.
В конечном итоге наше преобразование выглядит так: Projection*View*Model*(x,y,z,1). У итогового радиус вектора делим первые 3 координаты на 4-ю и получаем точку, готовую для рендера и z-теста.
Осталось перевести всё в экранные координаты. Поскольку у нас матричные преобразования перевели координаты точек в куб [-1,1], а координаты точек консоли 0..79 и 0..24, то нехитрыми операциями нужно выставить правильные координаты: (x+1.0)*0.5*80 и (y+1.0)*0.5*25.
Теперь надо выполнить z-test. Если получившееся значение z больше, чем то, которое там уже есть, то пиксель выводить на экран не надо. Иначе нужно записать в Color Buffer значение цвета пикселя и в z-buffer его z-координату.
Всё! Можно скачать демку и посмотреть!
В архиве исходники и исполняемые файлы для linux и windows
В статье описан наипростейший метод софтварного рендеринга. Конечно же, в реальных проектах используют многочисленные оптимизации, а процесс рендера гораздо сложнее и с более широкими возможностями.
Напоследок ещё скриншот из консоли ubuntu:

Добро пожаловать под кат!

Сегодня я расскажу вам от том, как написать простейший software 3D renderer.
Без всяких оптимизаций (что характерно для программ такого рода), т.к. моя главная цель — рассказать, как происходит 3D рендеринг, а не ускорение его работы.
Формат статьи не позволяет описать суть используемых алгоритмов и объяснять, почему, к примеру, матрицы преобразований выглядят так, а не иначе. В таких случаях я просто дам ключевые слова для поиска или ссылку и напишу, что оно должно делать. Прошу отнестись с пониманием :)
Итак, начнём:
Введение
В нашем случае простейший 3D рендерер будет включать в себя:
- Color Buffer — это просто массив, размеры которого равны размеру «экрана», а каждая ячейка хранит цвет «пикселя» (в нашем случае экран — это консоль размерами, например, 80х25, а пиксель — символ консоли — его «цвет» — это по сути код символа и его цвет в консоли)
- Depth Buffer — это массив, размеры которого такие же, как и у Color Buffer-a, но хранит он в себе значения «глубины» данной точки. Ведь поскольку мы проецируем трехмерное пространство на экран, то каждая точка имеет в себе некоторое значение координаты z по оси, перпендикулярной экрану. Нам это будет нужно для того, чтобы в случае перекрывания одних «пикселей» другими, на экран выводился тот пиксель, который ближе по z-координате (z-тест, подробнее — ниже)
- Растеризатор — по сути, это алгоритм, который по заданным трем точкам в координатах экрана генерирует все точки, образующие треугольник из заданных трех (также есть растеризатор линий — генерирует точки экрана, лежащие на линии, заданной своими концами). Это связано с тем, что мы будем использовать полигональный рендеринг, т.е. 3D-объекты, выводящиеся на экран заданы наборами треугольников в трехмерном пространстве.
- Матричные преобразования — это собтвенно преобразования координат треугольников из исходных в экранные (т.е. каждая точка c координатами x,y,z в трехмерном пространстве будет преобразована в точку с координатами x,y — точки на «экране» и z — значение глубины для z-буфера) ).
Опишу в общих чертах алгоритм рендеринга одного треугольника (таким образом, он будет повторяться для каждого треугольника, выводимого на экран).
- Преобразование координат каждой вершины из исходных координат в экранные. Для этого используются т.н. «однородные координаты». Необязательно знать, что это такое, достаточно понять, как этим пользоваться. Суть такова: к каждой вершине приписываем четвертую координату w=1. Затем выполняем умножение на 3 матрицы — World, View, Projection, потом берём вершину с координатами x/w,y/w,z/w и линейно преобразуем координаты x и y в координаты точки на экране (конкретное описание — ниже)
- Далее c помощью растеризатора из трёх точек на экране получаем экранные координаты всех точек треугольника и выполняем для каждой точки z-тест. Z-тест — это сравнение глубины точки на экране с глубиной точки, которую мы хотим вывести. Если выводимая точка лежит «дальше» той, что уже есть, то выводить ничего не надо. Таким образом мы можем рисовать 3D объекты в любом порядке, не заботясь о том, каки�� из них ближе, а какие дальше. Если у нас есть z-тест, то всё получится автоматически — ближние объекты будут закрывать дальние.
- После этого нужно просто вывести точку на экран. Для этого в Color Buffer записывается «цвет точки», а в z-buffer — её глубина.
Шаг 1. Color buffer и z-buffer
ColorBuffer и ZBuffer в нашем случае просто 2 массива 80х25 (это для примера, конечно же, всё зависит от размера консоли). Первый будет хранить символы консоли и, если хотите, их цвет. Второй — значения глубины для каждого пикселя. Это может быть float или double — любой тип данных, являющийся числом с плавающей точкой. Я реализовал это в виде шаблонного класса, где параметр шаблона — это тип данных, хранящийся в массиве.
Шаг 2. Растеризатор
Алгоритм растеризации нужен для построении пиксельного треугольника из заданных трех точек на экране их координатами x,y,z; Чтобы это понять и осознать, рекомендую почитать ru.wikipedia.org/wiki/Алгоритм_Брезенхэма для растеризации линии и далее используйте его для растеризации теугольника: compgraphics.info/2D/triangle_rasterization.php
Есть разные алгоритмы для этих целей, используйте любой, который понравится. Главное, чтобы была реализована функциональность генерации всех точек треугольника/линии по заданным экранным координатам (т.е. у меня, например, это будет в диапазоне 0..79, 0..24).
Или можете взять тот, который реализован у меня — есть функция растеризации треугольника, которая использует функцию растеризации линии, которая вызывает функцию растеризации точки, которая выполняет z-test и выводит точку на экран. (иголка в яйце, яйцо в утке, и т.д.)
На скорость работы я не обращаю внимание, поскольку так легче проследить логику работы. У себя, разумеется, можно что-нибудь соптимизировать.
Шаг 3. Преобразование координат
Итак, пусть у нас задана в трёхмерном пространстве точка с координатами x,y,z;
Я расскажу, как выполнить корректные преобразования Model-View-Projection для создания эффекта трёхмерности. Как я уже говорил, сначала мы делаем четырёхмерный вектор (x,y,z,1)
Самым первым выполняется преобразование Model. По сути это просто перенос/поворот/сжатие/растяжение или другое преобразование системы координат. Оно нужно для того, чтобы легко перемещать объект с течением времени — например у нас объект поворачивается на несколько град��сов вокруг оси Х каждые 10 мс. Соответственно, координаты модели мы храним как есть, а изменяем просто матрицу, задающую этот поворот.
Я приведу пример простейших матриц трёхмерного преобразования — перенос, поворот, сжатие.
Соответственно, для более сложных преобразований берите их композицию. Я представляю вектор как вектор-столбец и домножаю его на матрицу справа. Соответственно, если вам нужно сделать наоборот — транспонируйте матрицы и домножайте в другом порядке. Заметьте, что порядок перемножения самих матриц важен — если вы хотите повернуть объект и затем сделать перенос, то умножайте матрицу переноса на поворот и затем на координаты радиус-вектора точки. Итоговый вектор будет радиус-вектором преобразованной точки.
Примеры матриц:
Перенос (Translation)
(x,y,z) - вектор переноса
1 0 0 x
0 1 0 y
0 0 1 z
0 0 0 1
Растяжение/сжатие (Scale)
(x,y,z) - коэффициенты
x 0 0 0
0 y 0 0
0 0 z 0
0 0 0 1
Поворот вокруг оси х на угол α (Rotate)
1 0 0 0
0 cos α -sin α 0
0 sin α cos α 0
0 0 0 1
Поворот вокруг других осей делается аналогично: просто подставьте соответствующую матрицу поворота в верхнюю левую 3х3 подматрицу
Поворот вокруг произвольной оси: в OpenGL существует функция, которой можно скормить угол поворота и направление оси (любое), а она сама сгенерирует матрицу поворота и домножит на неё.
Функция просто вычисляет матрицу поворота, поэтому я не буду её здесь описывать. Её можно написать самим, нагуглить (называется glRotate) или взять из моего исходника (я уже погуглил за вас:)
Далее выполн��ется преобразование View. Наверное проще всего это объяснить через понятие «камеры». Если Вы играли в трёхмерные игры, то наверняка представляете себе, что это — это точка, из которой вы смотрите на игровой мир и ориентация камеры в пространстве этого мира. Для этого нужно выполнять преобразования, обратные вышеуказанным. Например, если надо взглянуть на мир из точки (1,2,3), то нужно сделать перенос (-1,-2,-3). Это логично — представьте себе, что объект 3D-мира имеет координаты (a,b,c). Тогда его матрица модели будет соответствующая — перенос a,b,c. Если при этом камера смотрит на мир из той же точки, то матрица view будет иметь вид: перенос -a,-b,-c и в итоге при перемножении View*Model*(x,y,z,1) мы получим исходные координаты объекта — таким образом камера находится там же, где и объект.
Тут ещё должны быть повороты для задания ориентации камеры. Дабы не усложнять никому жизнь, скажу лишь — погуглите функцию gluLookAt (эта статья и так большая, думаю, не стоит постить сюда исходник) или возьмите мой исходник — там тоже есть эта функция. Она генерирует матрицу View для заданных координат позиции камеры, направления взгляда и вектора up (без этого вектора ориентация камеры, очевидно, неоднозначна).
Что за матрица в итоге получается? Представьте, что у вас есть некоторая исходная система координат и вы делаете перемещение/поворот и получаете другую систему координат. Это преобразование задаётся некоторой матрицей. Если начало новой системы координат совпадает с позицией камеры, ось 'z' направлена по направлению взгляда, а 'y' — вверх, то матрица преобразование View — это обратная матрица этого преобразования. Конечно же, обратную матрицу никто не ищет — просто для получения ViewMatrix сразу делаются обратные преобразования.
И, наконец, Projection. Матрица проекции выполняет преобразование координат из пирамиды видимости (Frustum) в единичный куб (с учетом перспективы), после чего точку уже легко вывести на экран.
Frustum — это как раз та часть мира, которая проецируется на экран. Она представляет из себя усечённую пирамиду с двумя треугольниками в основании.

Я также не буду углубляться в объяснения об устройстве матрицы проекции, ясно, что она зависит от параметров znear, zfar (передняя и задняя плоскости отсечения), fovy (угол обзора по вертикали) и aspectratio (отношение ширины colorbuffer к высоте — для того, чтобы квадрат выглядел квадратом на прямоугольном экране, а не прямоугольником). Гуглите функцию gluPerspective или возьмите из моего исходника.
В конечном итоге наше преобразование выглядит так: Projection*View*Model*(x,y,z,1). У итогового радиус вектора делим первые 3 координаты на 4-ю и получаем точку, готовую для рендера и z-теста.
4. Итоговые преобразования
Осталось перевести всё в экранные координаты. Поскольку у нас матричные преобразования перевели координаты точек в куб [-1,1], а координаты точек консоли 0..79 и 0..24, то нехитрыми операциями нужно выставить правильные координаты: (x+1.0)*0.5*80 и (y+1.0)*0.5*25.
Теперь надо выполнить z-test. Если получившееся значение z больше, чем то, которое там уже есть, то пиксель выводить на экран не надо. Иначе нужно записать в Color Buffer значение цвета пикселя и в z-buffer его z-координату.
Всё! Можно скачать демку и посмотреть!
В архиве исходники и исполняемые файлы для linux и windows
Заключение.
В статье описан наипростейший метод софтварного рендеринга. Конечно же, в реальных проектах используют многочисленные оптимизации, а процесс рендера гораздо сложнее и с более широкими возможностями.
Напоследок ещё скриншот из консоли ubuntu:

