Эта статья посвящена созданию на ассемблере графического приложения весом в несколько сотен байт. После создания полноценной рабочей версии на 420 байт пришлось попотеть, чтобы запихать всё это добро в 256 байт. Результат вы можете лицезреть на видео. В статье описывается процесс создания и общие принципы функционирования.
Предупреждение: Если вы страдаете приступами эпилепсии — НЕ СМОТРИТЕ.
В Win7 и Vista работать не будет. Нужна Windows XP/2000/98.
Скачать исполняемый файл: k29.com в DropBox (256 байт)
Скачать исходный код: k29.asm в DropBox (Компилировать FASM-ом)
Клавиши управления:
1. R,G,B — включение и отключение цветовых компонент
2. <--,SPACE,--> — менять направление и скорость вращения
3. UP, DOWN — менять масштаб спирали
4. 0,1,2,3,4,5,6,7,8,9 — менять число ветвей у спирали
5. ESC — выход
Уже довольно долго эта статья валяется у меня в черновиках. Ещё в черновиках на Blogger-е валялась. И сегодня я решил, что если не допишу её сейчас — это не произойдёт никогда. Дописал, в конце немного оборвал и закончил) Ура!!!
Меня всегда интересовали работы с demoparty, особенно категории исчисляющиеся в сотнях байт. Одно дело писать прогу в 64 кило, используя DirectX/OpenGL, и совсем другое — в 512/256/128 байт, используя видеопамять напрямую и т.д. Тут необходимо знание и понимание ассемблера уже на интуитивном уровне. Необходимо уметь оптимизировать код по объёму, а значит понимать и учитывать все тонкости машинного языка программирования. Мы попробуем сделать что-то подобное. Я никогда раньше не писал на ассемблере, но разобраться в существующем коде получалось. Будем считать, что данная статья ориентирована на новичков в ассемблере вроде меня. Потому не претендую на идеальное решение задачи.
Теперь нужно придумать себе задачу и воплотить её. Мне на ум сразу пришла небольшая программа, написанная в школьные годы на языке Pascal. Программа была проста до безобразия (2 экрана кода — 50 строк), но в то же время она доставляла. Программа рисовала в графическом режиме (320x200x256) во весь экран вращающуюся спираль. Были задействованы все 256 цветов, для плавного изменения цвета. Было удивительно, что спираль движется без видимой перерисовки. Это можно было бы объяснить использованием нескольких видеостраниц, если бы не скорость вращения. Очевидно, что для отрисовки спирали необходимы вычисления с вещественными числами, что тоже вносит значительную задержку. Спираль вращалась со скорость 3-5 оборотов в секунду (см. рис. 2.1).

[ Рис. 2.1. Снимок спирали с тремя «руками» ]
А вся фишка была в том, что спираль рисовалась всего один раз — при запуске программы. После отрисовки спирали программа циклически сдвигала цвета в палитре, что незамедлительно отображалось на экране. Помимо основной функции программа поддерживала изменение цвета спирали и изменение направление вращения. Всего восемь цветов:
Так как для отображения на экране используется цветовая модель RGB, то эти восемь цветов можно получать, комбинируя соответствующие цветовые компоненты (3 бита данных могут кодировать 8 различных значений). Программа использовала клавиши 'R', 'G' и 'B' для вкючения/отключения соответствующих цветовых компонент.
Программа была написана на языке Pascal в среде разработки Turbo Pascal 7.0. Некоторые функции программы были реализованы в виде ассемблерных вставок. Например, функция установки RGB-значения конкретному элементу из палитры. Код школьных времен (форматирование изменено чтобы не травмировать ничью психику):
Сперва разберёмся в том, как функционирует программа и какие функции нам потребуется написать. Формальное описание алгоритма:
1) Начальное заполнение палитры следующими значениями: (0,0,0)... (63,63,63)... (0,0,0). Иными словами, на протяжении 256-ти элементов палитры цвет плавно меняется от черного к белому и снова возвращается к черному. В данном графическом режиме поддерживается до 256 цветов, каждый из цветов состоит из трёх цветовых компонент. Каждая из цветовых компонент задаётся шестью битами (число от 0 до 63). Белому цвету соответсвует вектор цветовых компонент (63,63,63), а чёрному соответственно — (0,0,0).
2) Отрисовка спирали включает в себя проход по всем пикселям экрана и заполнение их данными. Формула спирали достаточно проста — зависит лишь от вектора (пара значений: расстояние и угол), указывающего на конкретный пиксель из центра экрана. Иными словами цвет зависит только от длины вектора и угла вектора с подобранными коэфициентами. Перебирая различные коэффициенты можно получить как различное число «ветвей» у спирали, так и различную степень её закрученности.
3) Циклический сдвиг палитры на одну позицию. Это и даёт иллюзию вращения спирали. То есть, изменяя 256 элементов цветов, мы получаем сдвиг спирали на 1/(256*k) полного оборота. Где k — количество «ветвей» спирали. Таким образом мы избежали перерисовки всех пикселей экрана для вращения спирали. На самом деле сдвигать мы будем не на «одну» позицию, величина и направление сдвига хранятся в специальной целочисленной переменной. Это позволит нам динамически менять направление и скорость вращения спирали.
4) Проверка нажатий клавиш. Нажатие клавиш R, G и B ведет к включению, либо отключению закреплённой за каждой из клавиш цветовой компоненты. Нажатие на клавиши «вправо»/«влево» увеличивает/уменьшает значение переменной, которая явным образом используется при сдвиге палитры. Переход на пункт 3.
Чтож, теперь определим, какие функции нам потребуется написать на ассемблере. Очевидно, это будут: функция первоначального заполнения палитры, функция отрисовки спирали, функция циклического сдвига палитры и главная функция программы, которая помимо вызова вышеперечисленных функций будет обеспечивать проверку нажатий на клавиатуре управляющих клавиш. Блок-схема алгоритма:
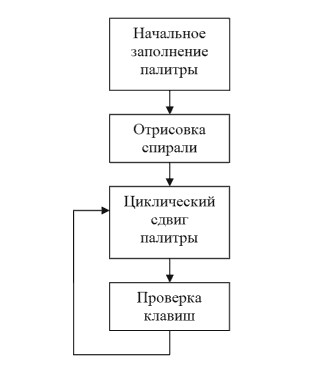
[ Рис. 4.1. Блок-схема алгоритма ]
Прочитав об имеющихся компиляторах языка ассемблер в википедии и книге «Искусство дизассемблирования» Криса Касперски и Евы Рокко, я сделал свой выбор в пользу компилятора FASM. Код буду писать в Notepad++, из него же и буду экспортировать в статью с подсветкой синтаксиса.
Ну чтож, приступим.
Мы собираемся заполнять палитру следующими значениями: (0,0,0),... (63,63,63),... (0,0,0). Нетрудно посчитать, что их всего 127, для равномерного заполнения всех 256 элементов будем заполнять по 2 одинаковых элемента: (0,0,0), (0,0,0),... (63,63,63), (63,63,63),... (0,0,0), (0,0,0). Запишем алгоритм на формальном языке высокого уровня:
Теперь ассемблерный код с комментариями:
A. Сохраняем в стеке и восстанавливаем из стека регистры, которые используются в функции.
B. Регистр CX пробегает в цикле от 0 до 127 включительно.
C. Формируем параметры и вызываем функцию setPalette. В AL загружаем индекс цвета, в AH загружаем значение яркости, равное половине индекса.
D. Меняем индекс на (255-i) используя операцию инверии всех битов и вызывает функцию setPalette.
Подумаем над функцией описания градиентной спирали.
Функция зависящая только от радиуса даёт градиентные окружности:

[ Рис. 4.1. Градиентные окружности ]
Функция зависящая только от угла даёт градиентные лучи из центра:

[ Рис. 4.2. Градиентные лучи ]
Функция же линейно зависящая от радиуса и угла даст нам искомую градиентную спираль:

[ Рис. 4.3. Градиентная спираль ]
Необходимо лишь подобрать необходимые коэффициенты, для 360-тиградусной правильной отрисовки спирали. Коэффициент k1 влияет лишь на степень закрученности спирали. Для правильного заполнения 360-ти градусов выберем коэффициент k3 таким:

[ Рис. 4.4. Правильная 360-тиградусная градиентная спираль ]
Коэффициент k2 будет принимать целочисленные значения: 1, 2, 3, 4... Меняя этот кофициент, мы получаем соответствующее число ветвей у спирали. Примеры градиентных спиралей при k2 равном единице, двум и пяти представлены на рис. 4.5, 4.6 и 4.7:

[ Рис. 4.5. Спираль с одной ветвью ]

[ Рис. 4.6. Спираль с двумя ветвями ]

[ Рис. 4.7. Спираль с пятью ветвями ]
Код отрисовки спирали на псевдо-языке:
(Без учёта возможных ошибок, в т.ч. деления на ноль)
Теперь реализуем алгоритм на ассемблере.
A. Сохраняем в стеке и восстанавливаем из стека регистры, которые используются в функции.
B. Регистр AX пробегает в цикле от 0 до 199 включительно.
C. Регистр BX пробегает в цикле от 0 до 319 включительно.
D. Сохраняем AX и BX в стеке. Выравниваем координаты центра спирали на экране, для разрешения 320x200 сдвигаем центр на середину — (160, 100). Восстанавливаем AX и BX из стека.
E. Возводим AX в квадрат, меняем местами значение регистров AX и BX, ещё раз возводим AX в квадрат. Имеем в регистрах AX и BX квадраты координат. Складываем значения регистров и загружаем результат в DX.
Вычислением корня вполне можно пожертвовать в пользу уменьшения размера кода приложения. Хорошо бы сохранить в стеке и восстановить обратно регистры AX и BX при вычислении длинны вектора:
Теперь код, вычисляющий акртангенс угла по заданным sin и cos:
Думаю код уже всех достал)) Вот где он лежит целиком: http://codepad.org/mEDX1Z2X
Ещё уменьшить объём кода можно, убрав лишние клавиши ��правления. Я думаю, если выкинуть всё управление можно легко уложится в 128 байт. Но без управления не так интересно.
Предупреждение: Если вы страдаете приступами эпилепсии — НЕ СМОТРИТЕ.
В Win7 и Vista работать не будет. Нужна Windows XP/2000/98.
Скачать исполняемый файл: k29.com в DropBox (256 байт)
Скачать исходный код: k29.asm в DropBox (Компилировать FASM-ом)
Клавиши управления:
1. R,G,B — включение и отключение цветовых компонент
2. <--,SPACE,--> — менять направление и скорость вращения
3. UP, DOWN — менять масштаб спирали
4. 0,1,2,3,4,5,6,7,8,9 — менять число ветвей у спирали
5. ESC — выход
Эпилог
Уже довольно долго эта статья валяется у меня в черновиках. Ещё в черновиках на Blogger-е валялась. И сегодня я решил, что если не допишу её сейчас — это не произойдёт никогда. Дописал, в конце немного оборвал и закончил) Ура!!!
1. Завязка
Меня всегда интересовали работы с demoparty, особенно категории исчисляющиеся в сотнях байт. Одно дело писать прогу в 64 кило, используя DirectX/OpenGL, и совсем другое — в 512/256/128 байт, используя видеопамять напрямую и т.д. Тут необходимо знание и понимание ассемблера уже на интуитивном уровне. Необходимо уметь оптимизировать код по объёму, а значит понимать и учитывать все тонкости машинного языка программирования. Мы попробуем сделать что-то подобное. Я никогда раньше не писал на ассемблере, но разобраться в существующем коде получалось. Будем считать, что данная статья ориентирована на новичков в ассемблере вроде меня. Потому не претендую на идеальное решение задачи.
2. Выбор цели
Теперь нужно придумать себе задачу и воплотить её. Мне на ум сразу пришла небольшая программа, написанная в школьные годы на языке Pascal. Программа была проста до безобразия (2 экрана кода — 50 строк), но в то же время она доставляла. Программа рисовала в графическом режиме (320x200x256) во весь экран вращающуюся спираль. Были задействованы все 256 цветов, для плавного изменения цвета. Было удивительно, что спираль движется без видимой перерисовки. Это можно было бы объяснить использованием нескольких видеостраниц, если бы не скорость вращения. Очевидно, что для отрисовки спирали необходимы вычисления с вещественными числами, что тоже вносит значительную задержку. Спираль вращалась со скорость 3-5 оборотов в секунду (см. рис. 2.1).

[ Рис. 2.1. Снимок спирали с тремя «руками» ]
А вся фишка была в том, что спираль рисовалась всего один раз — при запуске программы. После отрисовки спирали программа циклически сдвигала цвета в палитре, что незамедлительно отображалось на экране. Помимо основной функции программа поддерживала изменение цвета спирали и изменение направление вращения. Всего восемь цветов:
| 0 | #000000 | Чёрный (спираль не видно) |
| 1 | #0000FF | Голубой |
| 2 | #00FF00 | Ярко-зелёный |
| 3 | #00FFFF | Бирюзовый |
| 4 | #FF0000 | Красный |
| 5 | #FF00FF | Пурпурный |
| 6 | #FFFF00 | Желтый |
| 7 | #FFFFFF | Белый |
Так как для отображения на экране используется цветовая модель RGB, то эти восемь цветов можно получать, комбинируя соответствующие цветовые компоненты (3 бита данных могут кодировать 8 различных значений). Программа использовала клавиши 'R', 'G' и 'B' для вкючения/отключения соответствующих цветовых компонент.
Программа была написана на языке Pascal в среде разработки Turbo Pascal 7.0. Некоторые функции программы были реализованы в виде ассемблерных вставок. Например, функция установки RGB-значения конкретному элементу из палитры. Код школьных времен (форматирование изменено чтобы не травмировать ничью психику):
program P_16_B_4; uses crt,graph,MUSE_OTH,MT_MAIN; const koef1=3;{ Количество вихрей } koef2=3;{ Плотность вихрей } var gd,gm,gmx,gmy,i,flag,x0,y0,x,y:integer; r,alpha:extended; k,int:longint; key:char;rr,gg,bb:byte; ints:string; mas:array[0..255,1..3] of byte; BEGIN gd:=installuserdriver('SVGA256m.BGI',NIL);gm:=2; initgraph(gd,gm,''); gmx:=getmaxx; gmy:=getmaxy; flag:=1;k:=1; for i:=0 to 255 do begin setRGBpalette(i,k,k,k); mas[i,1]:=k;mas[i,2]:=k;mas[i,3]:=k; k:=k+flag; if k=63 then flag:=-1 else if k=0 then flag:=1; end; setcolor(63); settextstyle(1,horizdir,2); settextjustify(centertext,centertext); outtextxy(gmx div 2,gmy div 2-textheight('!<06@')*2 div 2, '!<06@ freeware'); outtextxy(gmx div 2,gmy div 2+textheight('!<06@') div 2, '! ! ! Press "R", "G", "B", " " or "Esc" ! ! !'); x0:=gmx div 2; y0:=gmy div 2; r:=400; repeat alpha:=0; repeat x:=round(x0+r*cos(alpha/180*Pi)); y:=round(y0-r*sin(alpha/180*Pi)); putpixel(x,y,round(r*koef2+alpha*256/360*koef1/2) mod 128); alpha:=alpha+20/(r+1); until alpha>=360; if keypressed then halt; r:=r-1; until r<=0; k:=1;flag:=-1;rr:=1;gg:=1;bb:=1;int:=0; repeat str(int SHR 2,ints); while byte(ints[0])<4 do insert('0',ints,1); if int and 3=0 then SAVE_MONITOR((gmx+1) div 2-75,(gmy+1) div 2-75,(gmx+1) div 2+74, (gmy+1) div 2+74,'c:\AVATAR\'+ints+'.bmp'); if keypressed then begin key:=readkey; if key=' ' then flag:=-flag else if upcase(key)='R' then rr:=not(rr) and 1 else if upcase(key)='G' then gg:=not(gg) and 1 else if upcase(key)='B' then bb:=not(bb) and 1 else if key=#27 then break; end; for i:=0 to 127 do setRGBpalette(i,mas[(i+k+512) mod 256,1]*rr, mas[(i+k+512) mod 256,2]*gg, mas[(i+k+512) mod 256,3]*bb); inc(k,flag);k:=k mod 256; inc(int); until false; closegraph; END.
3. Разработка алгоритма
Сперва разберёмся в том, как функционирует программа и какие функции нам потребуется написать. Формальное описание алгоритма:
1) Начальное заполнение палитры следующими значениями: (0,0,0)... (63,63,63)... (0,0,0). Иными словами, на протяжении 256-ти элементов палитры цвет плавно меняется от черного к белому и снова возвращается к черному. В данном графическом режиме поддерживается до 256 цветов, каждый из цветов состоит из трёх цветовых компонент. Каждая из цветовых компонент задаётся шестью битами (число от 0 до 63). Белому цвету соответсвует вектор цветовых компонент (63,63,63), а чёрному соответственно — (0,0,0).
2) Отрисовка спирали включает в себя проход по всем пикселям экрана и заполнение их данными. Формула спирали достаточно проста — зависит лишь от вектора (пара значений: расстояние и угол), указывающего на конкретный пиксель из центра экрана. Иными словами цвет зависит только от длины вектора и угла вектора с подобранными коэфициентами. Перебирая различные коэффициенты можно получить как различное число «ветвей» у спирали, так и различную степень её закрученности.
3) Циклический сдвиг палитры на одну позицию. Это и даёт иллюзию вращения спирали. То есть, изменяя 256 элементов цветов, мы получаем сдвиг спирали на 1/(256*k) полного оборота. Где k — количество «ветвей» спирали. Таким образом мы избежали перерисовки всех пикселей экрана для вращения спирали. На самом деле сдвигать мы будем не на «одну» позицию, величина и направление сдвига хранятся в специальной целочисленной переменной. Это позволит нам динамически менять направление и скорость вращения спирали.
4) Проверка нажатий клавиш. Нажатие клавиш R, G и B ведет к включению, либо отключению закреплённой за каждой из клавиш цветовой компоненты. Нажатие на клавиши «вправо»/«влево» увеличивает/уменьшает значение переменной, которая явным образом используется при сдвиге палитры. Переход на пункт 3.
4. Реализация алгоритма
Чтож, теперь определим, какие функции нам потребуется написать на ассемблере. Очевидно, это будут: функция первоначального заполнения палитры, функция отрисовки спирали, функция циклического сдвига палитры и главная функция программы, которая помимо вызова вышеперечисленных функций будет обеспечивать проверку нажатий на клавиатуре управляющих клавиш. Блок-схема алгоритма:

[ Рис. 4.1. Блок-схема алгоритма ]
Прочитав об имеющихся компиляторах языка ассемблер в википедии и книге «Искусство дизассемблирования» Криса Касперски и Евы Рокко, я сделал свой выбор в пользу компилятора FASM. Код буду писать в Notepad++, из него же и буду экспортировать в статью с подсветкой синтаксиса.
Ну чтож, приступим.
4.1. Функция первоначального заполнения палитры
Мы собираемся заполнять палитру следующими значениями: (0,0,0),... (63,63,63),... (0,0,0). Нетрудно посчитать, что их всего 127, для равномерного заполнения всех 256 элементов будем заполнять по 2 одинаковых элемента: (0,0,0), (0,0,0),... (63,63,63), (63,63,63),... (0,0,0), (0,0,0). Запишем алгоритм на формальном языке высокого уровня:
for (int i = 0; i <= 127; i++) { setPalette(i, i/2, i/2, i/2); setPalette(255-i, i/2, i/2, i/2); }
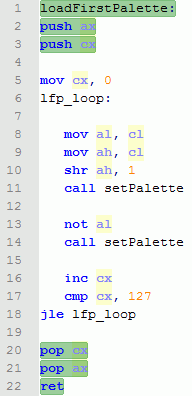
Теперь ассемблерный код с комментариями:
| A | B | C | D |
 |
 |
 |
 |
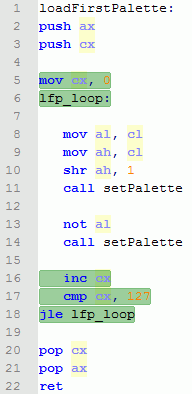
B. Регистр CX пробегает в цикле от 0 до 127 включительно.
C. Формируем параметры и вызываем функцию setPalette. В AL загружаем индекс цвета, в AH загружаем значение яркости, равное половине индекса.
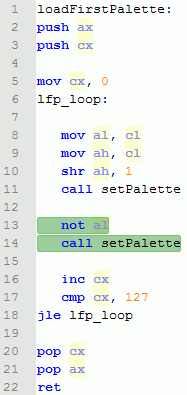
D. Меняем индекс на (255-i) используя операцию инверии всех битов и вызывает функцию setPalette.
4.2. Функция отрисовки спирали
Подумаем над функцией описания градиентной спирали.
Функция зависящая только от радиуса даёт градиентные окружности:
pixel[x][y] = k1*sqrt(x*x + y*y);

[ Рис. 4.1. Градиентные окружности ]
Функция зависящая только от угла даёт градиентные лучи из центра:
pixel[x][y] = k1*arctan(x/y);

[ Рис. 4.2. Градиентные лучи ]
Функция же линейно зависящая от радиуса и угла даст нам искомую градиентную спираль:
pixel[x][y] = k1*sqrt(x*x + y*y) + k2*k3*arctan(x/y));

[ Рис. 4.3. Градиентная спираль ]
Необходимо лишь подобрать необходимые коэффициенты, для 360-тиградусной правильной отрисовки спирали. Коэффициент k1 влияет лишь на степень закрученности спирали. Для правильного заполнения 360-ти градусов выберем коэффициент k3 таким:
k3 = 128 / 3.1415927;

[ Рис. 4.4. Правильная 360-тиградусная градиентная спираль ]
Коэффициент k2 будет принимать целочисленные значения: 1, 2, 3, 4... Меняя этот кофициент, мы получаем соответствующее число ветвей у спирали. Примеры градиентных спиралей при k2 равном единице, двум и пяти представлены на рис. 4.5, 4.6 и 4.7:

[ Рис. 4.5. Спираль с одной ветвью ]

[ Рис. 4.6. Спираль с двумя ветвями ]

[ Рис. 4.7. Спираль с пятью ветвями ]
Код отрисовки спирали на псевдо-языке:
(Без учёта возможных ошибок, в т.ч. деления на ноль)
for (int y = 0; y < 200; y++) for (int x = 0; x < 320; x++) { y -= 100; x -= 160; int color = k1*sqrt(x*x + y*y) + k2*128/3.1415927*arctan(x/y); y += 100; x += 160; pixel[x][y] = color; }
Теперь реализуем алгоритм на ассемблере.
| A | B | C | D | E |
 |
 |
 |
 |
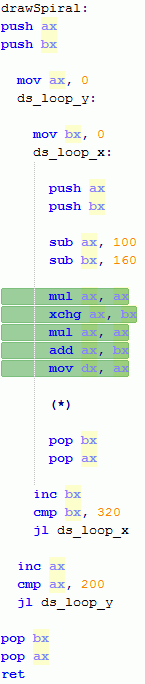 |
B. Регистр AX пробегает в цикле от 0 до 199 включительно.
C. Регистр BX пробегает в цикле от 0 до 319 включительно.
D. Сохраняем AX и BX в стеке. Выравниваем координаты центра спирали на экране, для разрешения 320x200 сдвигаем центр на середину — (160, 100). Восстанавливаем AX и BX из стека.
E. Возводим AX в квадрат, меняем местами значение регистров AX и BX, ещё раз возводим AX в квадрат. Имеем в регистрах AX и BX квадраты координат. Складываем значения регистров и загружаем результат в DX.
Вычислением корня вполне можно пожертвовать в пользу уменьшения размера кода приложения. Хорошо бы сохранить в стеке и восстановить обратно регистры AX и BX при вычислении длинны вектора:
push ax push bx ; dx = ax^2 + bx^2 mul ax, ax xchg ax, bx mul ax, ax add ax, bx mov dx, ax pop bx pop ax
Теперь код, вычисляющий акртангенс угла по заданным sin и cos:
; Вычисляем арктангенс угла * k2 ; dx += arctan(alpha * k2) mov [cos], ax mov [sin], bx finit fild word [cos] fild word [sin] fpatan fimul word [k2] fimul word [glad1] fidiv word [glad2] fist word [tmp] add dx, [tmp]
4.3. Проверка нажатий клавиш
; Проверка на нажатие клавиши mov ah, 0Bh ; AX := 0B00h int 21h cmp al, 0ffh jmp_loop_pal_exit: jne loop_pal_out ; Получаем какое именно нажатие mov ah, 08h int 21h label_push_space: cmp al, ' ' jne label_push_left mov ch, 0 label_push_left: cmp al, 75 jne label_push_right dec ch .......
Думаю код уже всех достал)) Вот где он лежит целиком: http://codepad.org/mEDX1Z2X
Ещё уменьшить объём кода можно, убрав лишние клавиши ��правления. Я думаю, если выкинуть всё управление можно легко уложится в 128 байт. Но без управления не так интересно.
