Всё началось с простой задачи: скачать по 100-мегабитной сети большой объём данных с помощью
После этого возник вопрос о анализе применимости распространённых программ сжатия
для передачи данных по сети.
Первой задачей было собрать исходные данные для анализа. Выбор подопытных пал на распространённые в *nix мире программы сжатия. Все программы были установлены из стандартных репозиториев Ubuntu 11.10:
Официальные сайты: lzop, gzip, bzip2, xz.
bzip2 основан на алгоритме BWT (англ.), остальные же основаны на алгоритме LZ77 (англ.) и его модификациях.
Для lzop степени сжатия 2-6 являются идентичными, и поэтому не тестировались.
Тестовая система представляла собой ноутбук на Intel P8600 (Core 2 Duo, 2.4 GHz)
c 4 GB оперативной памяти, работающий под Ubuntu 11.10 64-bit.
Для тестирования применялись несколько разных наборов данных:
Ну и более «классические» наборы:
Методика измерений была таковой: для каждой программы, степени сжатия, и исходного файла производилось сжатие в промежуточный файл с замером времени, затем запоминался размер сжатого файла,
затем производилась распаковка с замером времени. Распакованный файл на всякий случай сравнивался с исходным, затем промежуточный и распакованный файлы удалялись.
Для исключения влияния дискового ввода-вывода на результаты все файлы размещались в
Каждое измерение проводилось 3 раза. В качестве результата использовалось минимальное время из трёх.
Результаты приведены на графиках в координатах время упаковки — размер упакованного файла.
Рис. 1: График результатов для исходных кодов компилятора gcc:
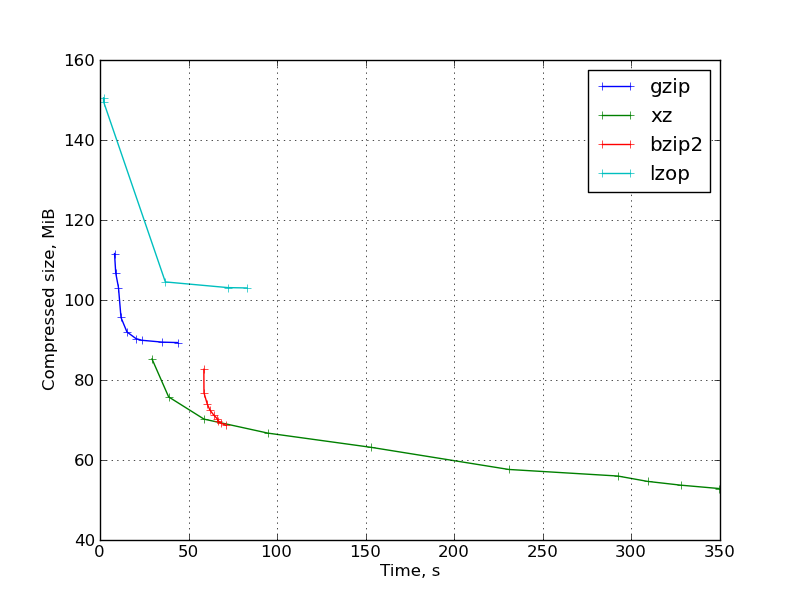
Рис. 2: График результатов для бинарного дистрибутива ParaView:
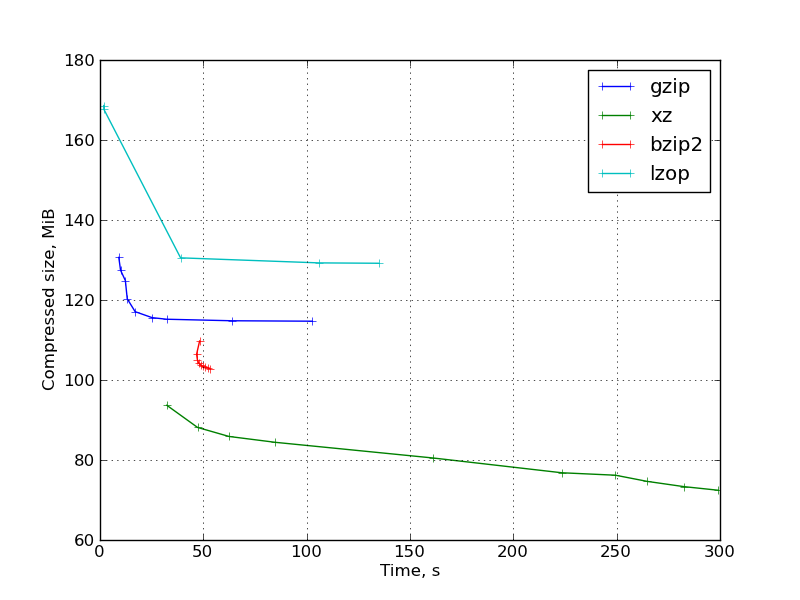
Рис. 3: График результатов для набора бинарных научных данных:
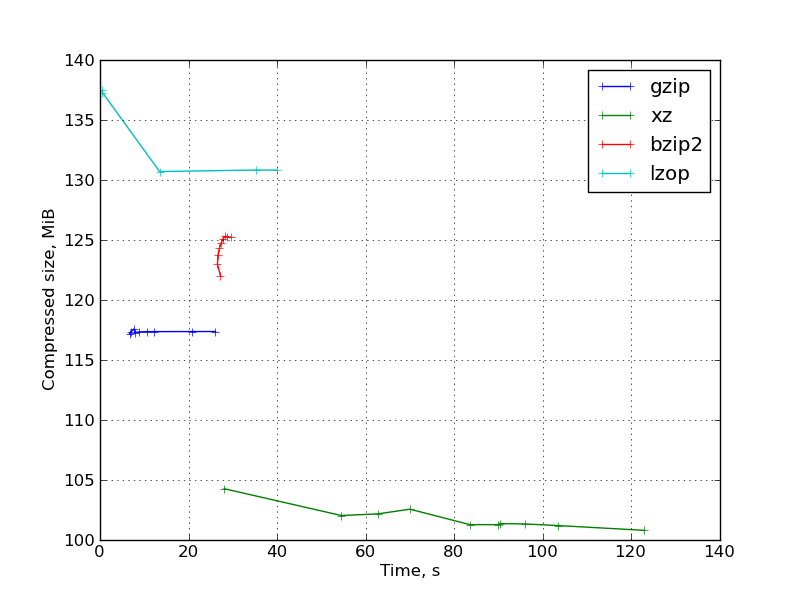
Также графики для: заголовков ядра и исходного кода OpenFoam.
Рассмотрим такой сценарий передачи данных по сети: сначала данные упаковываются, затем передаются по сети, затем распаковываются. Тогда общее время будет:
где
Это уравнение определяет кривую постоянного времени на приведённых графиках, наклон которой определяется пропускной способность сети. Чтобы определить оптимальный алгоритм упаковки для данной пропускной способности, нужно найти самую нижнюю прямую с нужным наклоном, проходящую через какую-либо точки графика.
То есть оптимальные методы сжатия и скорости их «переключения» определяются прямыми, касательными к нашему множеству точек на графике. Остаётся только определить их.
То что мы ищем, это не что иное, как выпуклая оболочка (англ. convex hull). Для построения выпуклой оболочки множества точек разработаны многочисленные алгоритмы. Мной использовалась реализация на питоне отсюда.
После построения выпуклой оболочки, точки, ей принадлежащие, будут нашими оптимальными алгоритмами, а наклоны рёбер, их соединяющих, будут граничными пропускными способностями.
Таким образом получаем такие оптимальные алгоритмы для наших файлов:
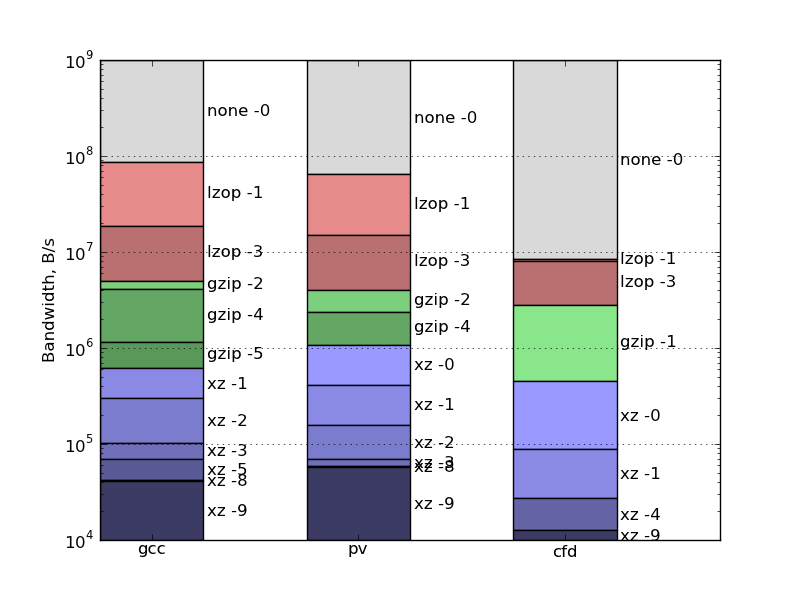
Теперь рассмотри другой сценарий: данные упаковываются, и сразу по мере упаковки отправляются по сети, а на приёмной стороне сразу распаковываются.
Тогда полное время передачи данных определяется не суммой, а максимумом из трёх времён: упаковки, распаковки, и передачи по сети.
Кривая постоянного времени для выбранной пропускной способности сети тогда будет выглядеть как угол с вершиной на прямой
и двумя лучами, идущими вниз и влево от вершины.
Алгоритм, позволяющий найти все оптимальные способы сжатия и граничные пропускные способности, в этом случае гораздо проще. Вначале мы сортируем точки по времени, затем выбираем первую оптимальную точку (это будет точка без сжатия, с нулевым временем. Отсутствие сжатия оптимально для сети бесконечной пропускной способности.) Теперь перебираем точки в порядке возрастания времени сжатия. Если размер файла меньше размера файла предыдущего оптимального метода, то текущий метод становится новым оптимальным. При этом граничная пропускная способность будет равна размеру файла предыдущего метода поделённому на время сжатия нового метода.
Вот результаты для такого сценария использования:

Известно, что один из самых быстрых каналов доставки больших объёмов информации на небольшие дистанции — велокурьер с жёсткими дисками.
Посчитаем. Пусть расстояние составляет 10 километров. Велокурьер сделает рейс туда-обратно за час-полтора (в нормальном темпе и с учётом всяких задержек, погрузки и разгрузки) Пусть это даст 6 рейсов за 8-часовой рабочий день. Пусть он возьмёт с собой 10 дисков по 1 ТБ. Тогда за день он перевезёт 60 ТБ. Это эквивалентно круглосуточной работе линии с пропускной способностью 60 ТБ / (24 * 3600) с = 662 МиБ/с что примерно составляет 5 Гбит/c. Неплохо.
По полученным результатам видно, что если пытаться сжимать данные для такой линии связи на одном ядре, аналогичном ядрам моего ноутбука, то оптимальным оказывается отсутствие сжатия.
А если же рассмотреть случай с переносом данных на одном USB 2.0 жёстком диске, то это ан��логично сценарию 2 со скоростью в примерно 30 МБ/сек, если мы учитываем затраты времени только на передающей стороне.
Глядя на наш график, получаем:
Если же мы сначала сжимаем, а затем копируем на внешний диск, то это сценарий 1, и тогда оптимальным по общим затратам времени для исходных кодов и бинарного дистрибутива оказывается
rsync. Возник вопрос, можно ли ускорить этот процесс. Утилита top показала, что на сервере-источнике шифрование занимает не более 10 процентов процессора, поэтому было решено что можно попробовать сжатие данных. Тогда мне было неясно, будет ли хватать производительности процессора для упаковки данных с необходимой скоростью, поэтому была выставлена самая маленькая степень сжатия, а именно использовался флаг --compress-level=1 для rsync. Оказалось, что загрузка процессора не превысила 65%, то есть производительности процессора хватило, при этом скорость скачивания данных несколько повысилась.После этого возник вопрос о анализе применимости распространённых программ сжатия
для передачи данных по сети.
Сбор исходных данных
Первой задачей было собрать исходные данные для анализа. Выбор подопытных пал на распространённые в *nix мире программы сжатия. Все программы были установлены из стандартных репозиториев Ubuntu 11.10:
Программа Версия Тестируемые ключи По умолчанию lzop 1.03 1, 3, 7-9 3 gzip 1.3.12 1-9 6 bzip2 1.0.5 1-9 9 xz 5.0.0 0-9 7
Официальные сайты: lzop, gzip, bzip2, xz.
bzip2 основан на алгоритме BWT (англ.), остальные же основаны на алгоритме LZ77 (англ.) и его модификациях.
Для lzop степени сжатия 2-6 являются идентичными, и поэтому не тестировались.
Тестовая система представляла собой ноутбук на Intel P8600 (Core 2 Duo, 2.4 GHz)
c 4 GB оперативной памяти, работающий под Ubuntu 11.10 64-bit.
Для тестирования применялись несколько разных наборов данных:
- Исходный код большого C++ проекта openfoam.com, пакованный в tar. Содержит исходный код, документацию в pdf, и некоторое количество плохо сжимаемых научных данных.
Несжатый объём: 127641600 байт = 122 МиБ
- Бинарный дистрибутив большого проекта paraview.org, упакованный в tar. Состоит в основном из .so файлов библиотек.
Несжатый объём: 392028160 байт = 374 МиБ
- Набор двоичных н��учных данных.
Несжатый объём: 151367680 байт = 145 МиБ
Ну и более «классические» наборы:
- Заголовки ядра linux, упакованные в tar.
Несжатый объём: 56657920 байт = 55 МиБ
- Исходный код компилятора gcc, упакованный в tar.
Несжатый объём: 490035200 байт = 468 МиБ
Методика измерений была таковой: для каждой программы, степени сжатия, и исходного файла производилось сжатие в промежуточный файл с замером времени, затем запоминался размер сжатого файла,
затем производилась распаковка с замером времени. Распакованный файл на всякий случай сравнивался с исходным, затем промежуточный и распакованный файлы удалялись.
Для исключения влияния дискового ввода-вывода на результаты все файлы размещались в
/run/shm (это общая память в linux, с которой можно работать, как с файловой системой).Каждое измерение проводилось 3 раза. В качестве результата использовалось минимальное время из трёх.
Результаты измерений
Результаты приведены на графиках в координатах время упаковки — размер упакованного файла.
Рис. 1: График результатов для исходных кодов компилятора gcc:

Рис. 2: График результатов для бинарного дистрибутива ParaView:

Рис. 3: График результатов для набора бинарных научных данных:

Также графики для: заголовков ядра и исходного кода OpenFoam.
Наблюдения:
- lzop при степенях сжатия 7-9 становится очень медленным без большого уменьшения размера файла, и очень сильно проигрывает в сравнении с gzip. Эти степени сжатия lzop совершенно бесполезны.
При степени сжатия по умолчанию lzop же, как и ожидалось, очень быстр. Степень сжатия -1 не даёт большого выигрыша по времени, давая больший размер файла.
- gzip ведёт себя вполне ожидаемо. «Правильная» форма графика при изменении степени сжатия.
- bzip2 оказался не очень конкурентоспособен. В большинстве случаев он проигрывает и по степени сжатия и по скорости низким степеням сжатия xz. Исключение составляют заголовки ядра и исходный код gcc (то есть чи��то текстовая информация), на которых они конкурируют. В этом свете довольно странно, что в интернете bzip2 пользуется несравненно большей популярностью, чем xz. Вероятно, это объясняется тем, что второй довольно молод и ещё не упел стать «стандартным».
Также стоит заметить, что разные ключи меняют степень сжатия и время работы bzip2 совсем незначительно.
- xz при больших значениях параметра демонстрирует высокую степень сжатия, но при при этом работает очень медленно и требует очень большого объёма памяти для сжатия (примерно 690 МБ при -9, требуемый размер памяти указан в мане). Размер памяти для распаковки существенно меньше меньше, но всё равно может стать
ограничением для некоторых применений.
Малые степени сжатия вплотную приближаются к gzip -9 по времени работы, обеспечивая лучшую степень сжатия.
Вообще же можно видеть что xz даёт довольно большой выбор соотношений степени сжатия и времени.
- Распаковка у основанных на LZ-77 программ происходит довольно быстро, причём с повышением степени сжатия (в пределах одной программы) время распаковки незначительно снижается.
У bzip2 распаковка происходит медленнее, причём время распаковки увеличивается с повышением степени сжатия.
Анализ: сценарий 1 — последовательные операции
Рассмотрим такой сценарий передачи данных по сети: сначала данные упаковываются, затем передаются по сети, затем распаковываются. Тогда общее время будет:
t = t_c + s/bw + t_d
где
t_c — время упаковки, s — размер упакованного файла в бай��ах,bw — пропускная способность сети в байтах/с, t_d — время распаковки.Это уравнение определяет кривую постоянного времени на приведённых графиках, наклон которой определяется пропускной способность сети. Чтобы определить оптимальный алгоритм упаковки для данной пропускной способности, нужно найти самую нижнюю прямую с нужным наклоном, проходящую через какую-либо точки графика.
То есть оптимальные методы сжатия и скорости их «переключения» определяются прямыми, касательными к нашему множеству точек на графике. Остаётся только определить их.
То что мы ищем, это не что иное, как выпуклая оболочка (англ. convex hull). Для построения выпуклой оболочки множества точек разработаны многочисленные алгоритмы. Мной использовалась реализация на питоне отсюда.
После построения выпуклой оболочки, точки, ей принадлежащие, будут нашими оптимальными алгоритмами, а наклоны рёбер, их соединяющих, будут граничными пропускными способностями.
Таким образом получаем такие оптимальные алгоритмы для наших файлов:

Анализ: сценарий 2 — потоковое сжатие
Теперь рассмотри другой сценарий: данные упаковываются, и сразу по мере упаковки отправляются по сети, а на приёмной стороне сразу распаковываются.
Тогда полное время передачи данных определяется не суммой, а максимумом из трёх времён: упаковки, распаковки, и передачи по сети.
Кривая постоянного времени для выбранной пропускной способности сети тогда будет выглядеть как угол с вершиной на прямой
t = s / bw
и двумя лучами, идущими вниз и влево от вершины.
Алгоритм, позволяющий найти все оптимальные способы сжатия и граничные пропускные способности, в этом случае гораздо проще. Вначале мы сортируем точки по времени, затем выбираем первую оптимальную точку (это будет точка без сжатия, с нулевым временем. Отсутствие сжатия оптимально для сети бесконечной пропускной способности.) Теперь перебираем точки в порядке возрастания времени сжатия. Если размер файла меньше размера файла предыдущего оптимального метода, то текущий метод становится новым оптимальным. При этом граничная пропускная способность будет равна размеру файла предыдущего метода поделённому на время сжатия нового метода.
Вот результаты для такого сценария использования:

Финальные замечания
- Всё написанное касается только сценариев с передачей больших объёмов данных, и не относится к другим сценариям, например с передачей множества мелких сообщений.
- Данное исследование имело имеет модельный характер и не претендует на полный учёт всех особенностей возникающих в реальной жизни. Вот некоторые из них:
- Не учитывается дисковый ввод-вывод.
- Не учитывается наличие и возможность использования нескольких ядер процессора.
- Не учитывается, что при серверном применении одновременно может присутствовать другая нагрузка на процессор, оставляя меньше ресурсов для сжатия.
- В данное исследование не включён snappy от гугла. Так получилось по нескольким причинам.
- Во-первых, у него нет родной утилиты командной строки (на самом деле есть сторонний snzip, но я не думаю что его можно считать сколько-нибудь стандартным).
- Во-вторых, он предназначен для других применений.
- В-третьих, он обещает быть ещё быстрее чем lzop, а значит, корректно замерить время его работы может оказаться очень трудно.
Практические примеры
Известно, что один из самых быстрых каналов доставки больших объёмов информации на небольшие дистанции — велокурьер с жёсткими дисками.
Посчитаем. Пусть расстояние составляет 10 километров. Велокурьер сделает рейс туда-обратно за час-полтора (в нормальном темпе и с учётом всяких задержек, погрузки и разгрузки) Пусть это даст 6 рейсов за 8-часовой рабочий день. Пусть он возьмёт с собой 10 дисков по 1 ТБ. Тогда за день он перевезёт 60 ТБ. Это эквивалентно круглосуточной работе линии с пропускной способностью 60 ТБ / (24 * 3600) с = 662 МиБ/с что примерно составляет 5 Гбит/c. Неплохо.
По полученным результатам видно, что если пытаться сжимать данные для такой линии связи на одном ядре, аналогичном ядрам моего ноутбука, то оптимальным оказывается отсутствие сжатия.
А если же рассмотреть случай с переносом данных на одном USB 2.0 жёстком диске, то это ан��логично сценарию 2 со скоростью в примерно 30 МБ/сек, если мы учитываем затраты времени только на передающей стороне.
Глядя на наш график, получаем:
lzop -3 оптимален для переноса данных на внешнем USB жёстком диске для наших тестовых наборов данных.Если же мы сначала сжимаем, а затем копируем на внешний диск, то это сценарий 1, и тогда оптимальным по общим затратам времени для исходных кодов и бинарного дистрибутива оказывается
lzop -1, а для плохо сжимаемых бинарных данных — отсутствие сжатия.Дополнительные ссылки
- Аналогичное сравнение: http://stephane.lesimple.fr/wiki/blog/lzop_vs_compress_vs_gzip_vs_bzip2_vs_lzma_vs_lzma2-xz_benchmark_reloaded
- Ещё сравнение: http://www.linuxjournal.com/node/8051/
