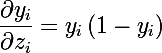Нейронная сеть с SoftMax слоем на c#

Привет, в прошлой статье я рассказал про алгоритм обратного распространения ошибки и привел реализацию, не зависящую от функции ошибки и от функции активации нейрона. Было показано несколько простых примеров подмены этих самых параметров: минимизация квадрата Евклидова расстояния и логарифмического правдоподобия для сигмоидной функции и гиперболического тангенса. Данный пост будет логическим продолжение прошлого, в котором я рассмотрю немного нестандартный пример, а именно функцию активации Softmax для минимизации перекрестной энтропии. Эта модель актуальна при задаче классификации, когда необходимо получить на выходе нейросети вероятности принадлежности входного образа одному из не пересекающихся классов. Очевидно, что суммарный выход сети по всем нейронам выходного слоя должен равняться единице (так же как и для выходных образов обучающей выборки). Однако не достаточно просто нормализировать выходы, а нужно заставить сеть моделировать вероятностное распределение, и обучать ее именно этому. Кстати, сейчас на coursera.org идёт курс по нейросетям, именно он помог углубиться в понимание софтмакса, иначе я продолжал бы использовать сторонние реализации.

Using

Рекомендую ознакомиться с предыдущим постом, так как все обозначения, интерфейсы и сам алгоритм обучения без изменений используются и здесь.

Функция активации softmax

Итак, первая задача, которая стоит перед нами, — это обеспечить способ моделирования сетью вероятностного распределения. Для этого создадим сеть прямого распространения, такую что:

• сеть содержит некоторое количество скрытых слоев, все нейроны могут иметь свою собственную функцию активации;
• на последнем слое находится такое количество нейронов, которое соответствует количеству классов; все эти нейроны будут называться softmax слоем или группой.

Нейроны softmax-группы будут иметь следующую функцию активации (в этом разделе я буду опускать индекс слоя, подразумевается, что он последний и содержит n нейронов):

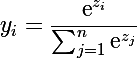• , для i-ого нейрона

Из формулы видно, что выход каждого нейрона зависит от сумматоров всех остальных нейронов softmax группы, а сумма выходных значений всей группы равняется единице. Прелесть данной функции и в том, что частная производная i-ого нейрона по своему сумматору равна:

• 
  

Реализуем эту функцию, используя интерфейс IFunction из предыдущей статьи:

Реализация softmax функции

Стоит отметить, что реализация метода double Compute(double x) вообще говоря не обязательна, так как вычисление выходных значений группы будет дешевле сделать в реализации softmax слоя. Но для полноты картины, да и на всякий случай пусть будет -)

internal class SoftMaxActivationFunction : IFunction
{

    private ILayer _layer = null;
    private int _ownPosition = 0;

    internal SoftMaxActivationFunction(ILayer layer, int ownPosition)
    {
        _layer = layer;
        _ownPosition = ownPosition;
    }

    public double Compute(double x)
    {
        double numerator = Math.Exp(x);
        double denominator = numerator;
        for (int i = 0; i < _layer.Neurons.Length; i++)
        {
            if (i == _ownPosition)
            {
                continue;
            }
            denominator += Math.Exp(_layer.Neurons[i].LastNET);
        }
        return numerator/denominator;
    }

    public double ComputeFirstDerivative(double x)
    {
        double y = Compute(x);
        return y*(1 - y);
    }

    public double ComputeSecondDerivative(double x)
    {
        throw new NotImplementedException();
    }
}

Функция ошибки

На каждом обучающем примере мы будем получать выход сети, который моделирует нужное нам вероятностное распределение, а для сравнения двух вероятностных распределений необходима корректная мера. В качестве такой меры будет использоваться перекрестная энтропия:

• 
• t — требуемые выходы для текущего обучающего примера
• y — реальные выходы нейросети

А общая ошибка сети вычисляется как:


Чтобы осознать элегантность всей модели, необходимо увидеть, как вычисляется градиент по одной из выходных размерностей или нейрону. В предыдущем посте в разделе «выходной слой» описано то, что задача сводится к вычислению dC/dz_i, продолжим с этого момента:

• , т.к. выход каждого нейрона содержит сумматор текущего, нам приходится продифференцировать всю сумму. В связи с тем, что функция стоимости зависит только от выходов нейронов, а выходы только от сумматоров, то можно разложить на две частные производные. Далее рассмотрим по отдельности каждый член суммы (главное обращать внимание на индексы, в нашем случае j пробегает по нейронам softmax группы, а i — это текущий нейрон)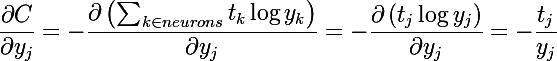
• 

  ---

• 

  ---

• 

  ---

• 

Последнее преобразование получается благодаря тому, что сумма значений выходного вектора должна равняться единице, по свойству нейронов softmax-группы. Это важное требование к обучающей выборке, иначе градиент будет подсчитан не верно!

Перейдем к реализации, используя то же представление, что и раньше:

Реализация перекрестной энтропии

internal class CrossEntropy : IMetrics<double>
{

    internal CrossEntropy()
    {
    }

    /// <summary>
    /// \sum_i v1_i * ln(v2_i)
    /// </summary>
    public override double Calculate(double[] v1, double[] v2)
    {
        double d = 0;
        for (int i = 0; i < v1.Length; i++)
        {
            d += v1[i]*Math.Log(v2[i]);
        }
        return -d;
    }

    public override double CalculatePartialDerivaitveByV2Index(double[] v1, double[] v2, int v2Index)
    {
        return v2[v2Index] - v1[v2Index];
    }
}

Softmax слой

Вообще говоря, особый слой можно и не делать, просто в конструкторе обыкновенной сети прямого распространения создавать последний слой, с функцией активации приведенной выше, и передавать ей в конструктор ссылку на софтмакс слой, но тогда при вычислении выхода каждого нейрона каждый раз будет высчитываться знаменатель функции активации, но если реализовать метод double[] ComputeOutput(double[] inputVector) нейросети должным образом:

public double[] ComputeOutput(double[] inputVector)
{
    double[] outputVector = inputVector;
    for (int i = 0; i < _layers.Length; i++)
    {
        outputVector = _layers[i].Compute(outputVector);
    }
    return outputVector;
}

то из-за того, что сеть не вызывает метод Compute нейрона напрямую, а делегирует эту функцию слою, можно сделать так, чтобы знаменатель функции активации вычислялся один раз.

Softmax слой

internal class SoftmaxFullConnectedLayer : FullConnectedLayer
{

    internal SoftmaxFullConnectedLayer(int inputDimension, int size)
    {
        _neurons = new INeuron[size];
        for (int i = 0; i < size; i++)
        {
            IFunction smFunction = new SoftMaxActivationFunction(this, i);
            _neurons[i] = new InLayerFullConnectedNeuron(inputDimension, smFunction);
        }
    }

    public override double[] Compute(double[] inputVector)
    {
        double[] numerators = new double[_neurons.Length];
        double denominator = 0;
        for (int i = 0; i < _neurons.Length; i++)
        {
            numerators[i] = Math.Exp(_neurons[i].NET(inputVector));
            denominator += numerators[i];
        }
        double[] output = new double[_neurons.Length];
        for (int i = 0; i < _neurons.Length; i++)
        {
            output[i] = numerators[i]/denominator;
            _neurons[i].LastState = output[i];
        }
        return output;
    }

}

Итог

Итак, недостающие детали готовы, и можно собирать конструктор. Я, например, использую одну и ту же реализацию сети прямого распространения, просто с другим конструктором.

Пример конструктора

/// <summary>
/// Creates network with softmax layer at the outlut, and hidden layes with theirs own activation functions
/// </summary>
internal FcMlFfNetwork(int inputDimension,
    int outputDimension,
    int[] hiddenLayerStructure,
    IFunction[] hiddenLayerFunctions,
    IWeightInitializer wi,
    ILearningStrategy<IMultilayerNeuralNetwork> trainingAlgorithm)
{
    _learningStrategy = trainingAlgorithm;

    _layers = new ILayer[hiddenLayerFunctions.Length + 1];
    _layers[0] = new FullConnectedLayer(inputDimension, hiddenLayerStructure[0], hiddenLayerFunctions[0]);
    for (int i = 1; i < hiddenLayerStructure.Length; i++)
    {
        _layers[i] = new FullConnectedLayer(_layers[i - 1].Neurons.Length, hiddenLayerStructure[i], hiddenLayerFunctions[i]);
    }

    //create softmax layer
    _layers[hiddenLayerStructure.Length] = new SoftmaxFullConnectedLayer(hiddenLayerStructure[hiddenLayerStructure.Length - 1], outputDimension);


    for (int i = 0; i < _layers.Length; i++)
    {
        for (int j = 0; j < _layers[i].Neurons.Length; j++)
        {
            _layers[i].Neurons[j].Bias = wi.GetWeight();
            for (int k = 0; k < _layers[i].Neurons[j].Weights.Length; k++)
            {
                _layers[i].Neurons[j].Weights[k] = wi.GetWeight();
            }
        }
    }
            
}