Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
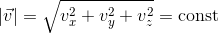 постоянен, то, как правильно заметил x0wl, может спокойно изменяться направление скорости, ибо она вектор
постоянен, то, как правильно заметил x0wl, может спокойно изменяться направление скорости, ибо она вектор 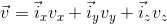 . Второй закон Ньютона формулируется для векторов:
. Второй закон Ньютона формулируется для векторов:  (приобретаемое ускорение равно силе, делёной на массу). Проще говоря, куда сила, туда и ускорение. Бывает, что есть ускорение без силы, которое необходимо вводить, если мы из лабораторной системы переходим в ускоренно движущуюся систему отсчета (она будет неинерциальна). Чтобы соблюсти правило сила->ускорение, то вводят нереальную силу инерции. Именно она Вас толкает в метро, когда вагон разгоняется или тормозит, именно она придавливает в пол ускоренно поднимающегося лифта и т.п. Существует принцип эквивалентности Эйнштейна, гласящий, что локально сила инерции неотличима от гравитационной. Именно поэтому есть идея создавать искусственное тяготение на космическом корабле путем его вращения вокруг своей оси. Ведь, при вращении в с/о, связанной с вращающимся космическим кораблем, возникают центробежные ускорение и сила (эффективные), и центростремительное ускорение которое их уравновешивает и создается реальными силами (к примеру, трения или реакции опоры).
(приобретаемое ускорение равно силе, делёной на массу). Проще говоря, куда сила, туда и ускорение. Бывает, что есть ускорение без силы, которое необходимо вводить, если мы из лабораторной системы переходим в ускоренно движущуюся систему отсчета (она будет неинерциальна). Чтобы соблюсти правило сила->ускорение, то вводят нереальную силу инерции. Именно она Вас толкает в метро, когда вагон разгоняется или тормозит, именно она придавливает в пол ускоренно поднимающегося лифта и т.п. Существует принцип эквивалентности Эйнштейна, гласящий, что локально сила инерции неотличима от гравитационной. Именно поэтому есть идея создавать искусственное тяготение на космическом корабле путем его вращения вокруг своей оси. Ведь, при вращении в с/о, связанной с вращающимся космическим кораблем, возникают центробежные ускорение и сила (эффективные), и центростремительное ускорение которое их уравновешивает и создается реальными силами (к примеру, трения или реакции опоры). . А это уже совсем другой объект с другими математическими свойствами; б) как следствие, Вы аппросимируете производные разностями (строите разностные схемы). Значение этих «разностей» уже отличаются от настоящей производной. Примером может служить уже упомянутое уравнение колебаний
. А это уже совсем другой объект с другими математическими свойствами; б) как следствие, Вы аппросимируете производные разностями (строите разностные схемы). Значение этих «разностей» уже отличаются от настоящей производной. Примером может служить уже упомянутое уравнение колебаний 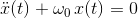 . Решением должен быть синус-косинус, но на практике явный метод Рунге-Кутта любого порядка точности даст нарастающую гармоническую функцию (к примеру, некоторое время назад этот эффект наблюдали тут). Дело в том, что при разностной аппроксимации Вы вносите в исходное уравнение член, пропорциональный
. Решением должен быть синус-косинус, но на практике явный метод Рунге-Кутта любого порядка точности даст нарастающую гармоническую функцию (к примеру, некоторое время назад этот эффект наблюдали тут). Дело в том, что при разностной аппроксимации Вы вносите в исходное уравнение член, пропорциональный  . Это трение с отрицательным коэффициентом. То есть, описывает приток энергии. Вещь, конечно же, хорошо известная. Например, тут мужик хорошо это рассказывает. Какой бы численный метод решения чего бы то ни было Вы ни брали, всегда будет раздел «устойчивость метода». Она зависит от шага сетки, порядков аппроксимации и т.д. Если Вы выбрали параметры метода, не удовлетворяющие критериям устойчивости, то численное решение не будет сходится, пусть даже само решение исходной задачи есть и устойчиво во всех смыслах.
. Это трение с отрицательным коэффициентом. То есть, описывает приток энергии. Вещь, конечно же, хорошо известная. Например, тут мужик хорошо это рассказывает. Какой бы численный метод решения чего бы то ни было Вы ни брали, всегда будет раздел «устойчивость метода». Она зависит от шага сетки, порядков аппроксимации и т.д. Если Вы выбрали параметры метода, не удовлетворяющие критериям устойчивости, то численное решение не будет сходится, пусть даже само решение исходной задачи есть и устойчиво во всех смыслах.
Моделирование электрического поля средствами CUDA